2.png)
トップページ > フーリエ変換入門(FFT入門) > 収束定理(9)
当初の目的は,「フーリエ級数が様々な関数 f(x) に収束するのを証明する」 ことでした。もう一度,頭から流れを確認していきます。
まずはフーリエ級数を途中で止めた「フーリエ有限和 SN(x) 」 を考えます。 “ N ”はフーリエ級数の項の数を表しています。 (「有限項のフーリエ級数」参照です。)
2.png)
そしてこの N を無限に飛ばす,すなわち「フーリエ無限級数」にすれば,f(x) に一致することを示したいのでした。よって,次式が証明すべき式となります。 (これも「有限項のフーリエ級数」参照です。)
_f(x)_lim3.png)
改めて,上式に SN(x) の中身を表示すると次のようになります。
-f(x)1.png)
ここで,a0,an,bn というのは「フーリエ係数」で, それぞれ以下のようにして計算するものです。 (「フーリエ係数(2)」参照です。)
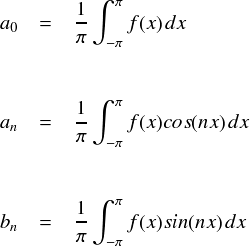
フーリエ係数の計算式を,そのまま代入してしまいます。 ただし,関数そのものの独立変数は「 x 」で, フーリエ係数部分の積分変数は「 y 」としています。
-f(x)4.png)
上式を三角関数の性質等を利用して整理すると,次のようになります。 ただし,変数変換を行い「 z = y - x 」としています。 (「ディリクレ核(1)」参照です。)
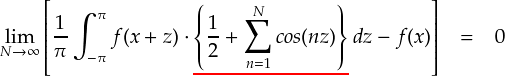
上式の赤線の部分は「ディリクレ核」と呼ばれる関数です。 ディリクレ核を,さらに三角関数の性質を利用して変形します。 (「ディリクレ核の中身をまとめる」参照です。)
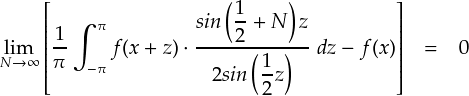
上式を少し変形すると,次のようになります。
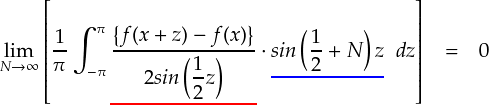
上式と,次式の「リーマン・ルベーグの定理」を見比べます。

上の二つの極限式は同一の形式となっています。 よって,最終的にリーマン・ルベーグの定理を適用することにより証明完了します。
なんて,上手くはいきません。。。
上の流れで見た最後の部分ですが,リーマン・ルベーグの定理を満たすためには条件がありました。

赤線の部分, f(x) には 「発散しない」という条件が必要なのでした。 リーマン・ルベーグの定理を満たす関数は,「発散しない」ことを含めて(発散しないことを必要条件として) 「区分的連続な関数」という条件を満たす必要がありました。 しかし,今回のディリクレ核などから変形してきた証明したい式を見ると,,,
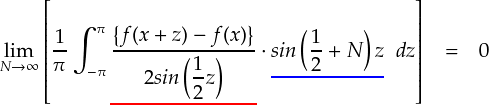
赤線の部分が リーマン・ルベーグの定理における f(x) に相当する部分です。 積分変数は z なので,動く変数 z に注目することにします。 すると, z = 0 で分母がゼロになることが分かります。発散・・・するのでしょうか? それだと困ります。 極限を取って調べてみます。
極限を調べたい部分を,次のように変形します。
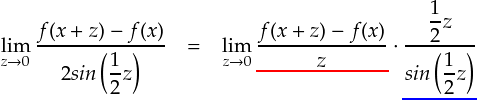
ここで,赤線の部分の極限は, f(z) の微分 となっています。
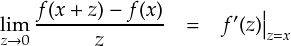
また,青線の部分はsin関数に関するおなじみの極限公式に当てはまっています。
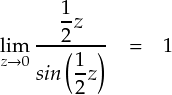
sinの部分は「1」に収束しているので発散しないことは分かりました。 よって,リーマン・ルベーグの定理を適用するのに必要な条件は f ' (x) が発散しないこととなります。これは「f(x)が微分可能」 という意味になります。 ここで,別に f(x) は別に連続・不連続に関する制限は受けていません。 よって,不連続関数でも良いということになります。 ・・・すると, 「不連続でもいいけど,発散しなくて,しかも微分可能」という条件になります。 これはまさに「f(x) が区分的なめらか」と同値です。
以上から,「ある関数f(x)が区分的なめらかな場合,フーリエ級数は収束し以下の式が成り立つ」 ことが証明されました。
-f(x)1.png)
はい。とりあえずひと段落です。
ここまでの話では,「フーリエ級数 S(x)」 が 「区分的なめらかな関数 f(x) 」に, どのような x でも収束する ということを証明しています。これを x の値1つ1つで収束するという意味から 「各点収束」 と呼ぶらしいです。
連続な関数なら,「各点収束」と言われてもイメージできますが, 不連続関数の不連続点ではどこに収束するのでしょうか? 先に結論を言ってしまうと,次のディリクレの収束定理 というのがあります。

上段の「 f(x) が連続の場合」は上で既に証明した通りです。 下段の「 f(x) が不連続の場合」が言ってることは, 「不連続点ではフーリエ級数は不連続点両端の平均に収束する」 ということです。間を取ってくれるんですね。確かにそれっぽいですが・・・ 一応証明しておきます。
基本的な流れは前と同じです。適当に変形→リーマン・ルベーグの定理 で終わりです。 要は,次の式を証明する感じです。
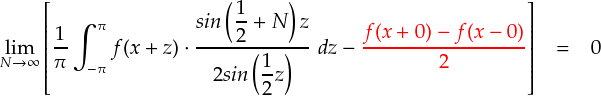
もうくどいほど解説したと思うので,最後は一気にいきます。
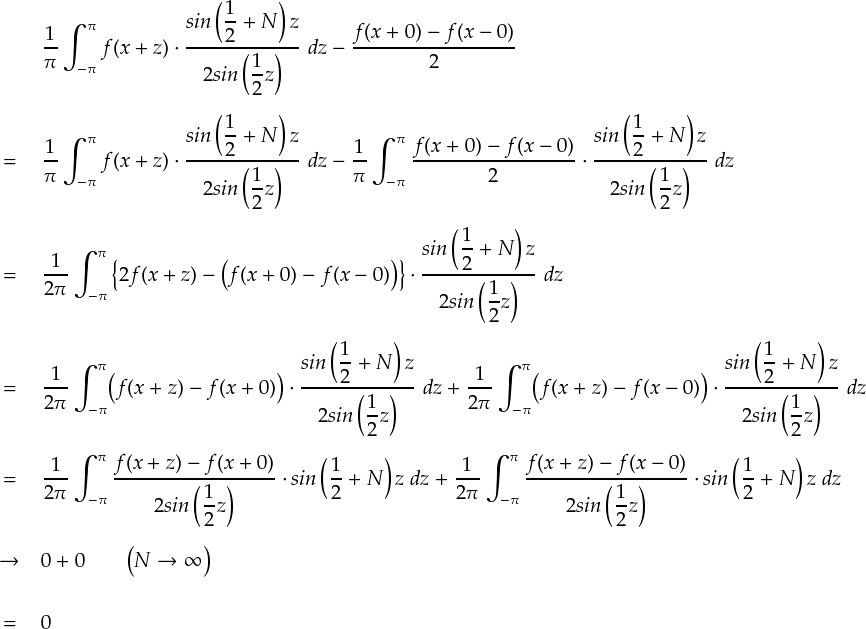
以上で「ディリクレの収束定理」の証明は終わりです。お疲れ様でした。。。
一番最初の,「フーリエ級数はどんな関数にも収束するの?」 という疑問に対する答えは,「相手が“区分的なめらか”な関数だったら収束する」という結論になりました。
今回証明したのは「ディリクレの収束定理」というやつで,電気信号を扱う上ではこれで十分かと思います。 アナログ信号を扱うのであれば,「電圧が無限大に発散する」なんてまずあり得ませんし,そもそも アナログ電圧で信号処理というのは普通行われない手法です。 普通にマイコンなんかで信号処理をする場合は「離散信号」を相手にすることになります。 (離散信号についてはまた後で。)いずれにせよ,これで十分だということで。
しかし,世の中にはフーリエ級数の収束について「○○の定理」みたいなものがたくさん存在するらしいです。 そういうマニアックな話は今回は省略します。。。
ここまで来ても,区分的なめらかな関数だったら sin 関数と cos 関数だけで表現できてしまうなんて,不思議です。。。 一応,もうひとつの疑問として「 sin と cos で全部基底は足りてるの?」というのがありましたが, ここまでの議論の延長ですぐに片付きます。次ページでやっつけます。