_f(x)_lim3.png)
トップページ > フーリエ変換入門(FFT入門) > 収束定理(3)
前ページからやっていることは,「フーリエ級数は様々な関数と一致するのか?」ということを確認する作業でした。 そのために証明したい式は,下式となっていました。
_f(x)_lim3.png)
SN(x) というのは,フーリエ級数を途中で止めた「フーリエ有限和 」 のことでした。ただしこのままでは扱いづらいので,いろいろいじりやすい形まで変形してきました。 それで,変形した結果が下式・・・という流れです。
-f(x)3.png)
それにしても,青いアンダーラインの部分( = SN(x))はゴチャゴチャしすぎている気がします。 ちょっと式変形してスッキリまとめることを試します。ここから先は,ダラダラと全部の式を書きならべても煩雑になるので,SN(x)だけを取り出して変形していきます。
式の整理の常套手段は,とりあえず共通因数でくくる・・・というやつでした。

上式を見ていると,ちょうど赤字の部分が共通です。これでくくり出してみます。 (シグマとインテグラルの位置を入れ替えることになりますが,積分してから総和をとっても, 総和をとってから積分しても,計算結果は変わりません。。。証明は略します。)
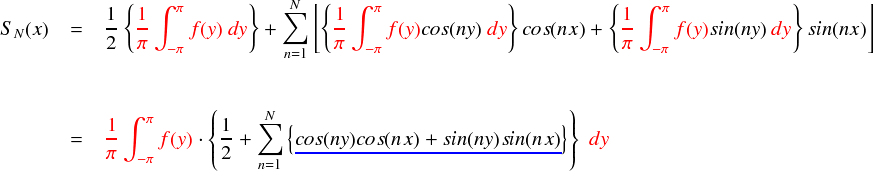
上式で青いアンダーラインを引いた部分は,cos関数の加法定理そのまんまの形をしています。
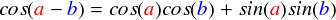
そんなわけで,これを使って整理します。
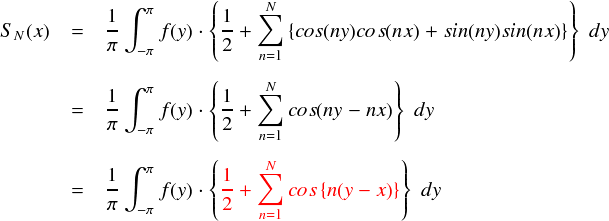
ここまでくると,だいぶSN(x) がスッキリ表わされるようになりました。 ここで,上式の赤色の部分は第 N 項までの級数の形になっています。 この級数の中のcosは変数が“(y-x)”となっていて気持ち悪いので,適当に変数変換してきれいにしておきます。
たとえば,y - x = z と,新しく文字zを導入して表わすことにします。
まず,「y」の置き換えと,積分変数の変換は次のようになります。
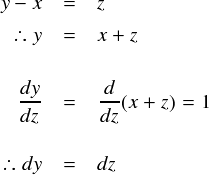
また,積分変数を「y」から「z」にするので,積分区間も修正します。
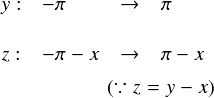
以上から,さっきの式は次のようになります。
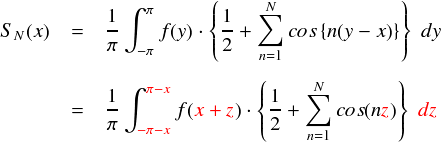
とりあえずcos関数のところは見やすくなりました。 しかし,積分区間に変数の「x」が含まれているがなんか嫌です。 周期関数の性質を使って,さらに修正します。
そもそも,今フーリエ級数で再現しようとしている「f(x)」は,sinやcosの寄せ集めで作るわけですから,当然周期関数ということになります。 f(x)を周期関数以外に対応させる話は,とりあえずフーリエ級数の収束の話を終わらせてからにします。(現状のフーリエ級数の注意点参照)
また,周期関数f(x)にかかっているのは1/2という定数と,cos(x)という周期関数になっています。
「周期関数×定数」は周期関数のままで,「周期関数×周期関数」もやはり周期関数になります。
よって,今回出てきた式は周期関数を積分していることが分かります。
ここで,周期関数を-π〜πで積分する時と,-π-x〜π-x まで積分する時とを比べてみます。
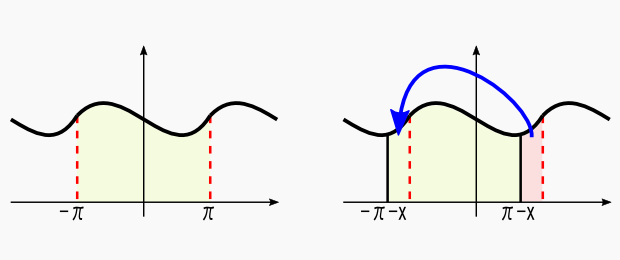
上の絵の通り,周期関数は積分区間をスライドさせても積分値(=面積)は同じになることが分かります。よって,さっきでてきた積分区間-π-x 〜π-x の積分も,-π〜πの積分として書き換えてしまいます。どう考えてもそのほうが分かりやすいので。。。
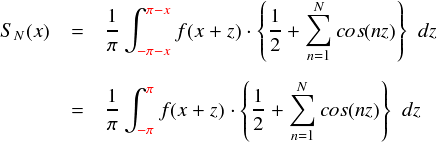
やっと式が短くなりました。これで一応完成です。。。
このページでは,ゴチャゴチャしていたフーリエ有限和:SN(x) を見やすく整理することを考えてここまできました。結局,SN(x) は次式のようになっています。
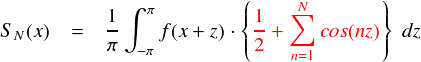
この赤色の部分はcos関数の級数となっています。 これを「ディリクレ核」(Dirichlet Kernel)と呼ぶそうです。なんかインパクト強い名前・・・
ディリクレというのは人名だそうです。ディリクレさん(1805 - 1859)は,フーリエさんの弟子だったらしいです。 とりあえず,「核」という名前が付くからにはかなり重要な気がします。
このディリクレ核の部分だけを抜き出して核場合は,「D(x)」という記号を使います。 さらに,「第N項まであるディリクレ核」は,添え字を使って「DN(x)」と表記します。
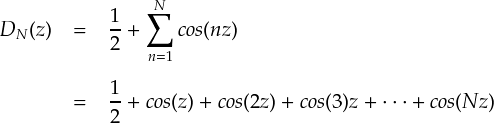
フーリエ級数の収束の問題はひとまず置いておいて, 次ページではこのディリクレ核をいろいろいじってみます。 実際,収束定理の証明に関して,このディリクレ核は重要な役割を持っています。