トップページ > フーリエ変換入門(FFT入門) > フーリエ級数(1)
前フリでは,「関数の基底」のイメージや,「三角関数の直交性」を確認しました。とりあえず今回は,全ての出発点である「フーリエ級数」の話です。
3次元ベクトルならば,任意のベクトルは3つの基底ベクトルを適当にミックスして作れるのでした。 「適当にミックス」というのは,各基底ベクトルの係数を好きなように設定して,どんどん足し合わせていく・・・という感じです。別に全ての基底を使う必要もないので,係数をゼロに設定してある基底を無効にするのもOKです。
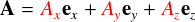
上の3次元ベクトルの形式を真似して,とりあえず適当に1つ関数をつくってみます。前フリでは,関数の基底として,
・・・が挙げられました。なので,今回はこれらが「基底ベクトル」なのだと思って,様々な関数を表す雛型というか,テンプレートというか,そんな感じのものを作ってみます。 一応,次式でどんな関数でも表現できるという気持ちです。
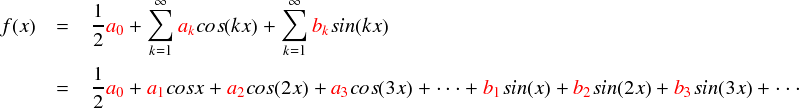
こうして出来上がった上のf(x)のことを,「フーリエ級数」と呼ぶそうです。 「級数」というのは関数とかをどんどん足し算したもののことでした。 単にベクトルに習って「係数×基底」の形を次々と足してみただけですが,今回の基底は三角関数なので,結果的に三角関数を次々と足し合わせた「級数」の形になっています。で,フーリエさんが考えた級数なので「フーリエ級数」という名前だそうです。そのまんま・・・。
一応,各項の係数について触れておきます。名前の付け方にもいろいろ意味が含まれているようです。
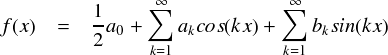
最初のa0は定数です。これはただの数なので,1つあれば十分。全体のオフセットみたいな役割です。 しかし,何故「1/2」が付いているのか。定数なんですから,単に“a0”だけで十分な気がします。 それでも実際に教科書を開いてみると,ほとんどの教科書ではa0の係数が1/2になっています。これには理由があって, 1/2を付けておくと後々になって式がキレイになる ・・・とか,そんな感じです。 (後で,a0を求めるのところで説明してます。)
で,cos関数とsin関数はありったけ出します。周波数が異なる三角関数は,「基底」としては全くの別モノでした。 なので,周波数が違うものには別々に係数を与えてしまいましょう。これを無限までやります。若干やりすぎ感がありますが,本気を出しているということで。。。
3次元ベクトルの時は基底が3つだけだったので,全ての項を書くといっても3つだけなのでそこまで面倒ではありません。 しかし,今回は項が無限にあります。そんなの書けません。なのでシグマ記号を使ってお手軽に済ませます。
あと,係数に使っているアルファベットについて。係数に a や b を使うのは数学ではおなじみです。cos関数の係数が a1,a2,a3... となっていて,sin関数の係数がb1,b2,b3,... となっています。この添え字の数は,それぞれの係数を持つsin関数・cos関数の周波数と同じになるようにしてあります。分かりやすくなるように工夫されています。
しかし,定数項を「a0」と書くのは違和感があるかもしれません。三角関数とは別のアルファベットを使えばいいのに・・・と思うところです。 これには理由があります。「cos(0) = 1」なんだから,数字を表すならcos関数の係数 a をそのまま使ってしまえ・・・というノリだったりします。添え字がゼロということも 「cos(0) = 1」を意識しているという感じです。 添え字がゼロとは,言い換えれば「周波数がゼロ」という意味です。つまり全く振動していない成分です。たしかに,定数をグラフに書けば一直線な関数でした。そんなわけで添え字が“0”なんだと考えることもできます。 もちろん,a0は1以外の様々な数字でOKです。
今回出てきたフーリエ級数 f(x)は,係数 a と b をいじれば様々な関数へフィットさせることができるつもりで作りました。 しかし,このフーリエ級数には大きな制限がついています。フーリエ級数はsin関数とcos関数からできているので,どう考えても「周期関数」です。その周期はいくつかというと,一番大きな周期をもつsin(x)とcos(x)から定まる「-π〜π」となります。他の,もっと細かいsinとcosは必ず-π〜πの間に収まっているはずですから。
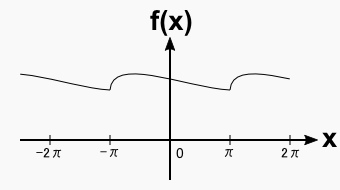
そんなわけで,フーリエ級数 f(x) が表現できるのは-π≦x≦πの間で2πの周期を持つ関数だけです。まあ,当たり前と言えば当たり前なんですけど。。。とりあえず今はこれで我慢しておきます。実は大した問題はなく,このf(x)をちょっといじるだけで「どんな関数でも」表現できるようになってしまいます。とりあえず, f(x) を周期に縛られないように改良する作業は後回しにします。
次は,自分が欲しい関数へフーリエ級数を近づけるために,係数 a と b をどう決めれば良いのかという話です。