トップページ > フーリエ変換入門(FFT入門) > フーリエ級数(3)
前ページではとりあえずフーリエ係数とは何なのか,そして cos(x) の項の係数である a1 を取り出す方法を確認しました。要はcos(x)と内積をとればいいわけです。ただそれだと,cos(x)のノルムの2乗である「π」が出てきて邪魔なので,最後にπで割っていたのでした。
今度は,一般化して,cos(nx)の係数である an を全部求めてしまいましょう。
1つ1つ計算するのも面倒なので,三角関数の直交性を確認した時と同様の方法で一気にやってしまいます。つまり,cos(x),cos(2x),cos(3x),...をまとめて「cos(nx)のフーリエ係数」として計算する感じになります。(nは自然数)
それでは,フーリエ級数 f(x) とcos(nx)の内積を計算してみます。前回と同様に,cos(nx)どうしの内積以外は全部ゼロになるので,最後に残るのはただ1つの項になります。
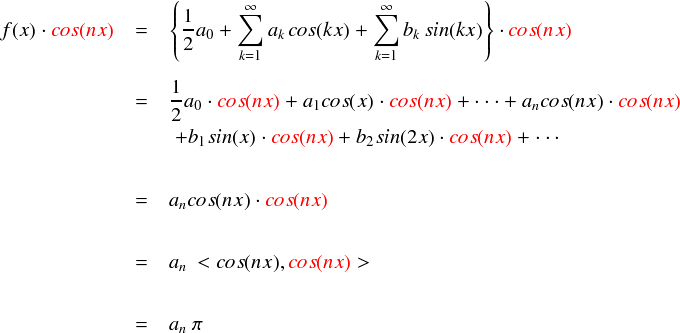
結局,cos(nx)と内積をとれば周波数nのcos関数の係数 an が出てくるわけです。 今回,n は自然数であれば何でも良いので,一応あらゆる an を求める式が完成したことになります。 例のごとく,直観的なベクトル形式でも見ておきます。
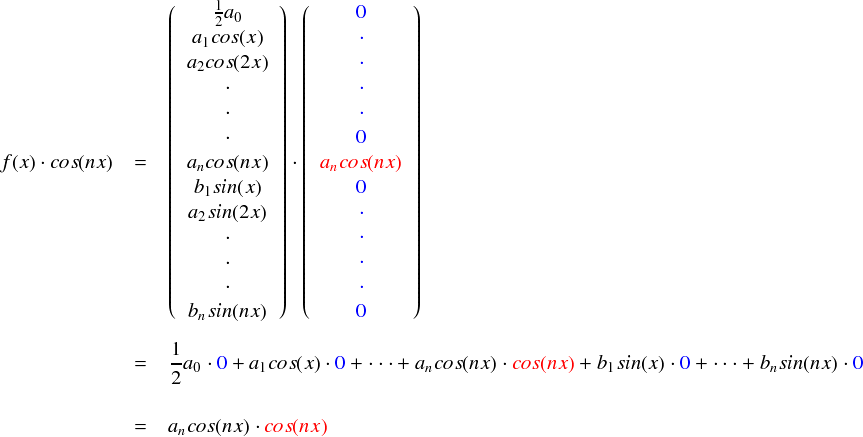
前回と同じ感じでした。。。ただし,毎回気をつけないといけないのですが,cos(nx)・cos(nx) の「・」という記号は単なるかけ算ではなく内積の記号です。そんなわけで,anを求める式として整理すると,
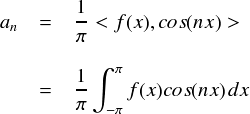
・・・という感じになりました。結局,「 cos(nx) と内積をとってπで割る」 ことでanを求めることができます。3次元ベクトルの場合とそっくりです。
anを一括して求めるための式が完成したので,次はbnを求める式を作ります。bnというのはフーリエ級数の中でsin関数の係数となっているものでした。よって,今度は フーリエ級数 f(x) と sin(nx)の内積を計算してみます。
くどいですが,おなじみの直交性を考えれば,sin(nx)どうしの内積以外は全てゼロになることが分かります。 そんなわけで,今回も最後まで残る項は1つだけになります。
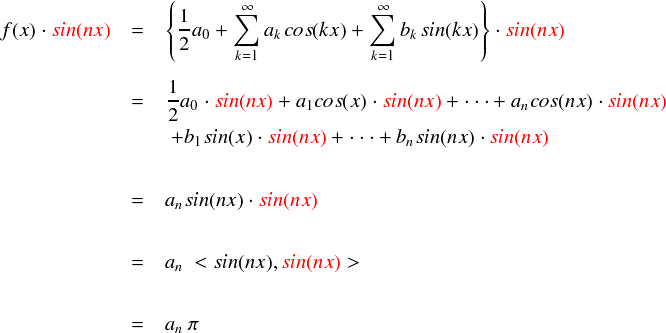
何度も同じ事ばかりで申し訳ないですが,< sin(nx), sin(nx) > の計算はsin(nx)のノルムの2乗である「π」が出てきます。では,言わずもがなですが,ベクトル風の式で直観的な理解を・・・。

それでは,bn を計算するための式に整理します。なんというか,計算過程が an とそっくりなので,結果も an と似たような感じになります。
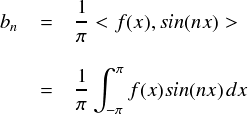
以上のことから,bnを計算する時は,「f(x)とsin(nx)で内積をとって,πで割る」 ことになります。これもまた,3次元ベクトルからの類推でイメージした通りという感じです。
cos関数の係数である an,sin関数の係数である bn ・・・ときたので,最後に定数項の a0 を計算します。 これを計算すれば,どうして定数項が単純に「a0」とは書かずに 「1/2a0」となっているのかが分かります。では,例のごとく, フーリエ級数 f(x) と定数 1 の内積 を計算します。
もう分かってるよ・・・という感じですが,三角関数であるsinとcosに対して,定数は直交しています。なので,またもや最後まで残るのは1つの項だけです。いいかげん面倒なので,ベクトル表記だけでやっつけます。
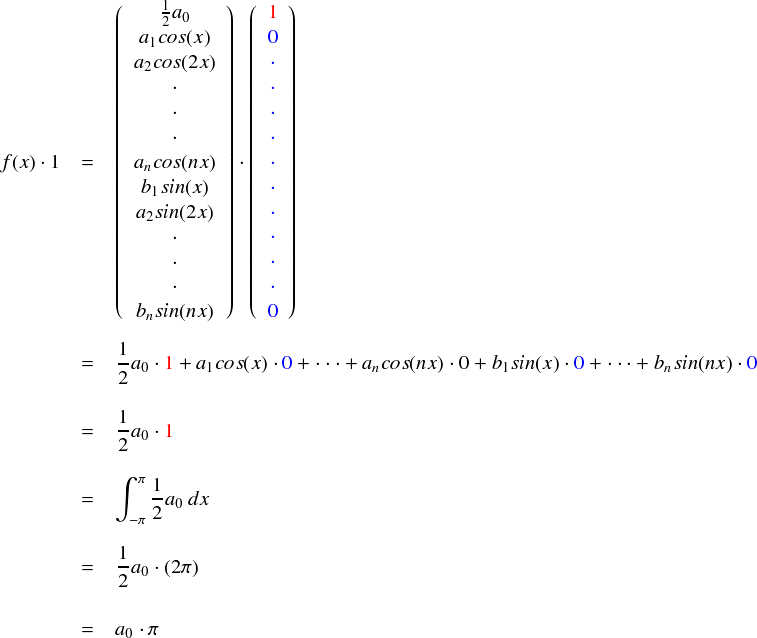
途中で出てきた「1/2 a0・1」というのも,ちゃんとした内積計算です。内積計算なので,ちゃんとこれまでと同様に-π〜πで積分しなければいけません。 ただし,今回は被積分関数はただの定数なので,単に 2π をかけ算するという結果になります。
a0を求める式として整理すると,次式のようになります。
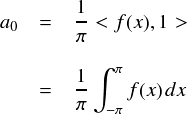
今回も, anやbnと同様にπで割る形となりました。 しかし,これはフーリエ級数の中の定数項を「1/2a0」と置いていたからであって, もし直観的に分かりやすいであろう「a0」と書いていたら2πで割ることになります。 おそらく,昔の人たちは「a0だけ2πで割る式になるなんて,美しくない」 ・・・とかなんとか考えてたんだと思います。まあ,公式として覚えやすいように統一してもらったと考えておきます。
結局,a0を求めるためには,単に「 f(x) を-π〜πで積分する」だけで良いと分かりました。 これは,-π〜πで f(x) の平均を取っている・・・と見ることもできます。
以上で,全てのフーリエ係数を計算するための方法が揃いました。
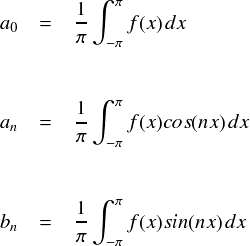
なんというか,全部同じに見えます・・・。 むしろ,頑張って統一したんだと思いますけど。 特に,a0なんかはフーリエ級数では「1/2a0」という若干不自然な書き方をしてまで,同じ形式で表せるように工夫されていたわけです。
ではでは,次は前フリで出てきた「矩形波のフーリエ級数」を導出してみます。