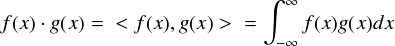
トップページ > フーリエ変換入門(FFT入門) > 前フリ(5)
前ページでは,関数の内積を計算する方法が分かりました。下式のような感じで,2つの関数をかけ合わせて積分するだけです。
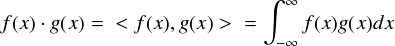
とりあえず,sinxとsin2xの内積を計算してみます。 この結果がゼロになれば「sinxとsin2xは直交している」, 言いかえると「sinxとsin2xは全く同じ成分を持たない」ということが示せます。 sinxとsin2xの内積は下式のようになります。

この式では,積分区間が-∞から∞までとなっています。 これは前ページで,「関数をベクトルと考えた場合にその要素は無限個ある」という話の流れからきています。 このまま計算するとちょっと面倒なことになるので,計算する前に三角関数の「周期性」を意識してみます。
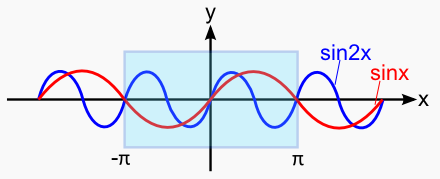
いま内積をとろうとしているのはsinxとsin2xですが,sinxは-πからπまでの波形が無限に繰り返されます。 sin2xの方は-π/2からπ/2の波形が,やはり無限に繰り返されています。いわゆるsinxの周期は2πで, sin2xの周期はπだという話です。
ここで,内積をとろうとしている目的は「sinxとsin2xの共通成分を知りたい」ということだったので, 無限に繰り返される波形のうち,「1周期」のブロックだけに着目して内積を取っても問題ない・・・ と考えてしまいます。周期としてはsinxの方が長いので,sinxの-π〜πに合わせて積分をすることにします。
たとえsin3x, sin4x, ... sinnx を相手にする場合でも,結局のところ一番周期が長いのはsinxです。 なので,今後は三角関数どうしの内積の場合は,常に積分区間を-π〜πとして計算することにします。 そうすれば,必ず1周期以上含まれるので内積をとる上では問題無いことになります。
積分範囲を-π〜πとしたので,内積の計算式は次式のようになります。
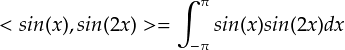
とりあえず,三角関数どうしの積の形は積和公式で和の形に変形するのが定石でした。 手計算では三角関数の積を積分することができないからです。 積和公式は,例のごとく加法定理をいじって作ります。
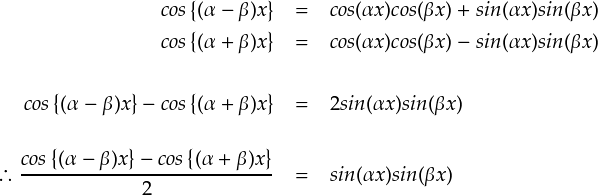
これを最初の式中のsinxsin2xの部分へ代入して,計算してしまいます。 今回はα=1,β=2 として積和公式を使います。
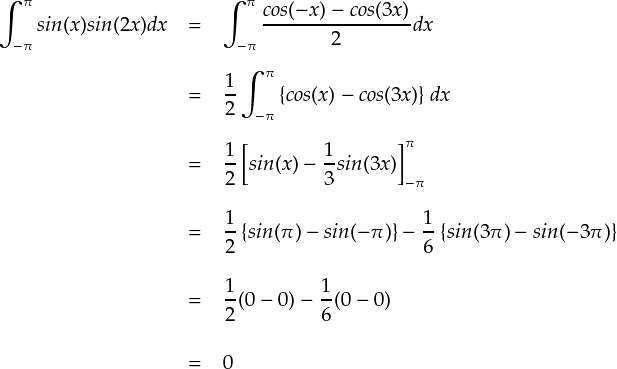
というわけで,めでたく内積がゼロになりました。まあ,ゼロにならないと困るのですが・・・。 一応これで「sinxとsin2xは直交している」ことを示せました。 sinxとsin2xは波形として,共通する成分を一切持っていません。
ここまでの話で,三角関数の(というか周期関数の)内積を計算する際には,積分区間を無限ではなく 1周期分で区切ってしまってよいということを確認しました。 また,少なくともsinxとsin2xは直交していることが分かっています。 しかし,sin(nx)なんて関数はいくらでも存在します。 その1つ1つの組み合わせをイチイチ計算して直交していることを確認するのは面倒すぎます。 そんなわけで,一般化してsin(mx)とsin(nx)という任意の整数mとnを含む形で内積をとってしまいます。
ではでは,さっそく計算してみます。
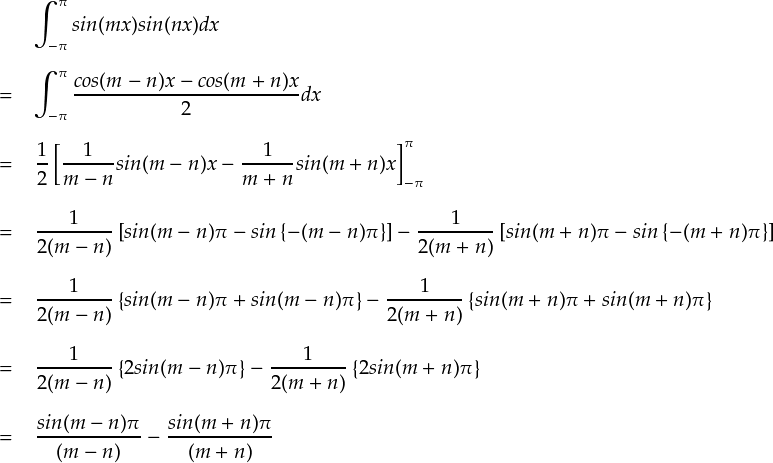
一番下の段の,第2項は楽です。mとnは整数だったので,(m+n)πは必ずπの整数倍ということになります。 すると,sin(m+n)π = 0が常に成り立っているので第2項は無視できます。
で,第1項が少々面倒です。分母に(m-n)というのが入っていて,m = n の時は分母がゼロになってしまいます。
そんなわけで,場合分けしていきます。
【m ≠ n の場合】
これは楽ですね。(m-n)は正負どちらか分かりませんが,とにかく整数です。よって,(m-n)πはπの整数倍となり,
sin(m-n)π = 0 が常に成り立つため第一項全体がゼロになります。
【m = n の場合】
この場合,分母・分子が共にゼロになってしまうので,極限計算を使います。
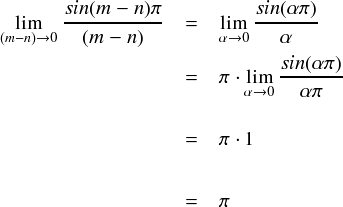
計算途中で,下式の公式を使っています。 (この式は高校数学で習うものだったか忘れてしまいました。。。一応,証明は後々どこかで書きたいと思ってますが,これは微積分学とかの話なので今回は省略します。)
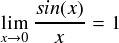
結局,ここまでの計算では次の結果が得られました。
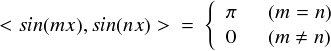
先ほど計算した結果について,どんなイメージを持てば良いのかを考えてみます。
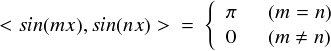
まず,下段の m ≠ n の場合は分かりやすいと思います。m ≠ n ということは,sin(mx)とsin(nx)は 違う三角関数ということになります。違う三角関数どうしであれば,どんな組み合わせであれ, 必ず内積はゼロになることが分かりました。これは期待通りというか,予想通りというか・・・。
次に,m = n の場合を考えます。m = n のときは,「自分自身と内積を取っている」ということになります。 ここでも,2次元ベクトルを考えて比較してみます。
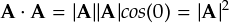
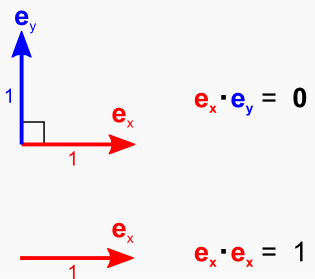
普通の,図でイメージできるようなベクトルでは,ベクトルが自分自身と内積を取ると,そのベクトルの長さの2乗が出てきます。
・・・ということは,計算結果にある「π」というのは 「三角関数をベクトルと見たときの“長さの2乗”」 のような物だと考えることができます。この値の平方根をとれば,「三角関数ベクトル」の長さになるはずです。 なんだか抽象的な話ですが,単に「式の形が同じなら,同じものと思っておこう」・・・くらいのノリだと思います。 この「関数が自分自身と内積をとった値」のことを「ノルム」と呼ぶそうです。このノルムは“||f(x)||”という記号を用いて表わされます。(たしか線形代数で習った気がします)
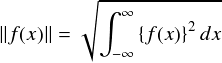
そんなわけで,sin関数のノルムは周波数によらずすべて√πだということになります。あとで規格化とかの話をする時に出てくるかもしれませんので,一応書きました。
次は,やり残しているcos関数の方も片付けます。