トップページ > フーリエ変換入門(FFT入門) > 前フリ(6)
前ページでは,sin関数は全て直交だということを確認しました。 しかし三角関数は sin だけではありません。cos関数はどーなってんだよ? とツッこまれてしまうかもしれません。 結論としては,全てのcos関数は直交してて,さらにsinとcosも直交なんです。 だから,sin,cosの両方が揃わないと任意の関数を表現できない・・・という話で終わります。 でも念のために計算しておきます。
前ページでやったのと同様に,cos(mx)とcos(nx)で内積をとってみます。
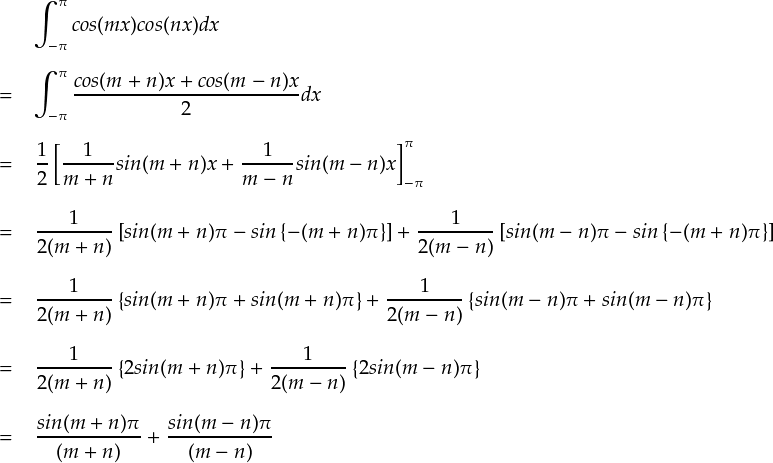
この結果は,sinでやった時と全く同じです。そんなわけで,やはりmとnに関して場合分けします。前ページと全く同じやり方で,下の結果がでます。
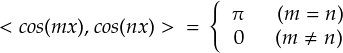
以上,cos関数どうしも直交していることが示せました。 全てのcos関数は,互いに共通成分を一切持っていません。 なんというか,cos関数も「基底」っぽくなってきました。 では,sin関数だけ,もしくはcos関数だけで全ての関数を表すことができてしまうのでしょうか。 またはsinとcos両方を合わせないとダメなのでしょうか。それを知るには,「sinとcosでは共通成分があるのか?」 ということを調べる必要があります。もし共通成分を持っていないなら,両方必要だと分かります。
そんなわけで,次はsinとcosで内積を計算します。
今度は,sin関数とcos関数で内積をとってみます。
sin関数とcos関数の積を扱うために,積和公式のもう1つのパターンを作っておきます。
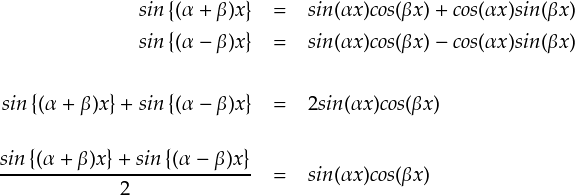
積和公式が準備できたので,一般化したsin(mx)とcos(nx)に関して内積を計算します。
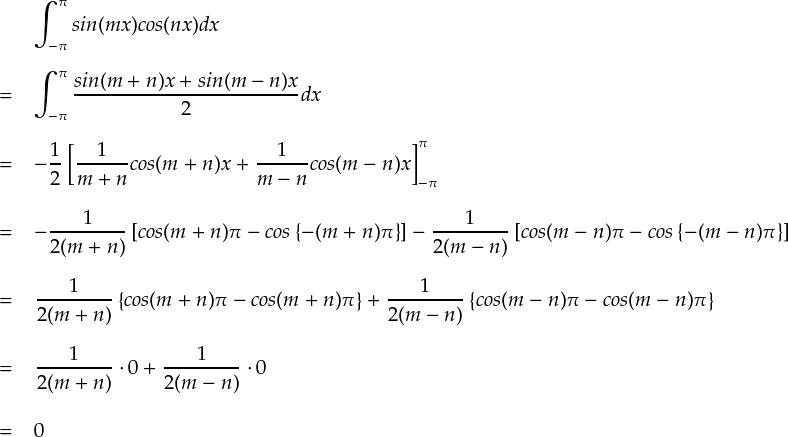
・・・というわけで,sin関数とcos関数も直交しています。 つまり,互いに共通成分を持たないので,sin関数とcos関数の両方を合わせないと 基底が不足してしまいます。 最初の例の矩形波では,たまたまsin関数だけで表せていましたが,そういうケースもあるというだけです。 全ての関数を表現できると言うためには,sin関数とcos関数の両方が必要です。
では,「一定値関数」のようなものでもsin関数とcos関数の組み合わせで表せるのでしょうか。 sin関数もcos関数も振動する関数ですので,変化が無い一定値関数を表現するのは難しそうです。 最後に,定数aとsin関数・cos関数の内積を確認します。
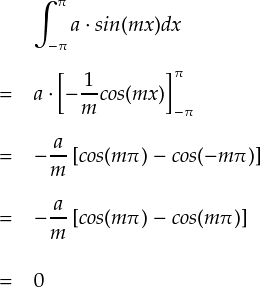
非常に単純な積分ですが,明らかにsin関数は「定関数」と直交しています。 cos関数についても同様にaを定数として内積を計算します。
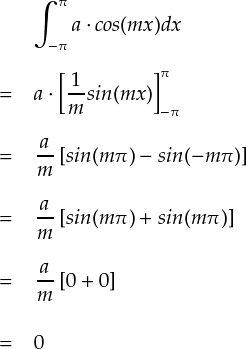
おなじく,上式からcos関数と定関数も直交していることが確認できます。 ・・・とすると,「定数」という基底も盛り込む必要があることに気づきます。
これで全部終わりです。おつかれさまでした。。。