トップページ > フーリエ変換入門(FFT入門) > 前フリ(7)
なんだか前フリだというのに,随分ダラダラと書いてしまいました。 これからの本筋に向けて,ここまでどんな話の流れだったのかを一度まとめて整理しておきます。
とりあえず前フリの重要ポイントは,以下の3点だと思います。
2次元平面上の任意の点を指定するためには, ex と ey の2つの基底ベクトルさえあれば十分なのでした。
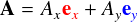
この類推から,関数にも基底のようなものがあって, それを組み合わせればどんな関数でも表すことができるのではないかと予想しました。 もし三角関数が基底であれば,確かにどんな関数でも三角関数のみで表すことができます。
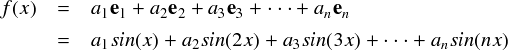
三角関数が「基底関数」であるのかを調べるために,関数の内積というものを考える必要が出てきました。
ベクトルにおいて,内積という計算の意味は「2つのベクトルで同じ成分を抽出すること」です。
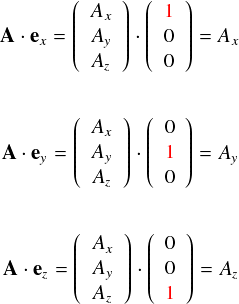
ベクトルの内積の計算方法から,関数の内積を計算する方法を考えました。 関数の内積を計算するには,2つの関数の積をとって,1周期にわたって積分します。 この方法は,2次元ベクトルの成分から内積を求める方法をもとにしています。
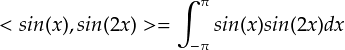
関数の内積の方法が分かったので,三角関数どうしの内積をどんどん計算していきました。 もし関数どうしの内積がゼロであれば,2つの関数の間には共通成分が一切無いことになります。 これを「直交」という言葉で表すのでした。
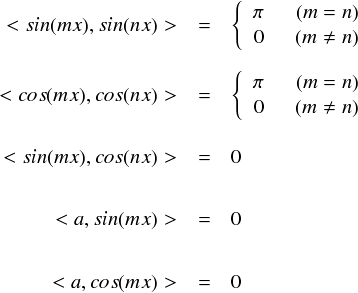
そして周波数が異なるsin関数どうし,周波数が異なるcos関数どうし,sin関数とcos関数どうし・・・ などの内積は,全て直交していることが分かりました。また,三角関数において自分自身と内積をとった値 (ノルムの2乗)はπになる,という話もありました。
あくまで前フリなので,まだまだ詰めが甘いところがたくさんあります。
次の「フーリエ級数」以降で,1つ1つ確認していきます。