トップページ > フーリエ変換入門(FFT入門) > 前フリ(4)
前ページの最後では,3次元のベクトルの基底は ex , ey , ez の3つがあるという話が出ました。
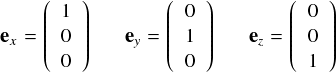
そして,「全ての3次元ベクトルは3つの基底ベクトルを伸び縮みさせれば表せる」ことを確認しました。
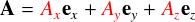
ここで,sin関数で矩形波を作る のところで出てきた, 「矩形波は周波数が異なるたくさんのsin関数の重ね合わせで作れる」(らしい)ということを思い出してください。 上の話とすごく似ています。もしかしたら「関数の基底」のようなものが存在して,それがまさにsin関数だったりするのでは? と予想しても良い気がします。。。
「関数の基底」とは言っても,どう扱ったら良いものか悩みます。 前ページで出てきたベクトルは3次元だったからこそ, x軸の基底ベクトルがexで,y軸の基底ベクトルはeyで・・・ みたいに名前を付けることができました。しかし,周波数が異なるsin関数なんて無限にあります。 ここは適当に,数字で e1, e2, e3,...と名前をつけておきます。 各基底ベクトル(?)の要素を,周波数が異なるsin関数で構成すると下式のような感じになります。 (一番上の式と見比べると,それっぽい感じになっています)
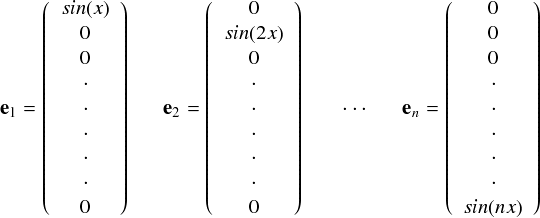
すると関数f(x)は2次元や3次元のベクトルからの類推で,やはり基底であるe の各成分に好きな係数 a1,a2,a3,... をかけてミックスすれば表せそうです。
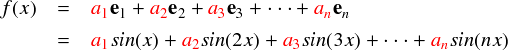
しかし,これはあくまで「予想」なので,本当に三角関数が様々な関数の基底になっているのかは分かりません。 そんなわけで,またもや2次元ベクトルに頼ります。。。2次元ベクトルの exやeyは「基底」だと分かりきっているので, その性質から類推すれば何かヒントが見つかるかもしれません。
基底ベクトルの ex や ey と内積を取れば,方向の成分だけが残るのでした。それでは,基底どうしの内積を取ったらどうなるのか? ということを考えてみます。
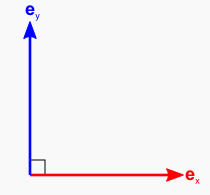
ex と ey の内積は, 図から見てとれる通り ex と ey が「直交」しているのでゼロです。cos90°= 0 だから,という感じで。
内積がゼロというのは, 「ex と ey には共通の成分が無い」という重要な意味を持っています。 なんというか,もし ex と ey で “かぶっている”成分があったら,もっとスマートな別の基底が選ばれているはずです。。。妥当な結果ではないでしょうか。
さらに,3次元の話になっても「直交している」という理由から, ex, ey, ez の成分が次のようになっていることが理解できます。
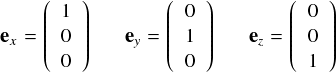
「共通の成分が無い」ので,x の基底はx方向のみに要素を持っていて他のyとzに関してはゼロです。 yの基底,zの基底に関しても同じ感じです。
さて,既に分かりきっている2次元や3次元の話では,基底ベクトルどうしが直交しています。 では,ここで非常に単純な発想をします。三角関数は様々な関数の基底かもしれない・・・という話が前ページで出たことから,「三角関数どうしは“直交”しているのか?」ということを知りたくなります。
突然「関数が直交している」と言われても意味不明です。しかし,三角関数どうしが直交していることが確認できれば,まずは基底っぽいと思うキッカケになると思います。 とはいえ,上のような感じで図を書いてイメージするのは3次元が限界です。「関数」なんてものをまるでベクトルのように考えるのは難しいかもしれません・・・
でも,なんとかして三角関数が全ての関数の基底であることを確認したいのです。そんなわけで,次は「関数をベクトルとして扱う」方法を考えてみます。
関数をベクトルっぽく見るために,なんとかしてみます。関数 f(x) というものは,x の値によって決まった値をとるのでした。 x が -∞ から ∞ まで動いたとき, f(x) はそれに合わせて無限個の値となります。「 x 」という入力が与えられると,「 f(x) 」が出力として1つの値だけ出てくるという感じです。
ここで,f(x)をxの値ごとにタテに並べて書いてみます。
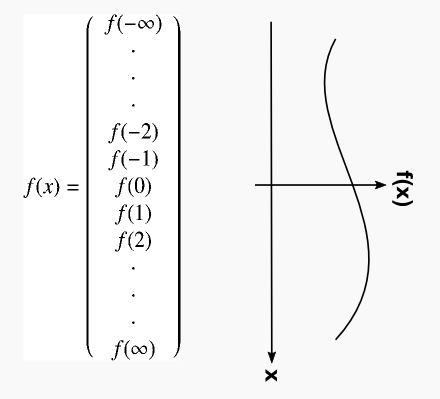
上式ではf(1),f(2),・・・のようにxの値が整数になっていますが,これは単に式を見やすくするためです。 実際にはf(0.000001), f(0.000002),・・・という感じでxは非常に細かく変化します。 というか,どんなに細かい数字を使っても「xは○○ずつ変化する」みたいな言い方には意味がありません。 これは,頭の中でイメージするしかありません。
こう書いてみると,関数は「無限次元のベクトル」のように見えます。とりあえずこれでいきましょう。 もし何か不都合が出たら,その時に修正しましょう。もし問題なければ,「関数はベクトルなんだ」と堂々と言えば良いだけのことです。
前ページでは普通の(?)2次元ベクトルどうしの内積計算を扱いました。それに対応して,今回は「関数の内積」というのを考えます。 内積の計算方法には図形的イメージによるものと,成分から求めるものと,2種類ありました。 n次元ベクトルでは図形的イメージは面倒なので,ここは成分から求める方法でいきます。
とりあえず,2次元ベクトルではこんな感じでした。
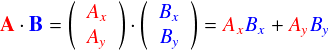
ベクトルの1つ目の要素同士をかけ算,2つ目の要素どうしをかけ算,・・・とやって,最後にそれらを全部足し合わせます。
ではでは,上の真似をして何か適当な f(x) と g(x) という関数どうしで内積をとってみます。
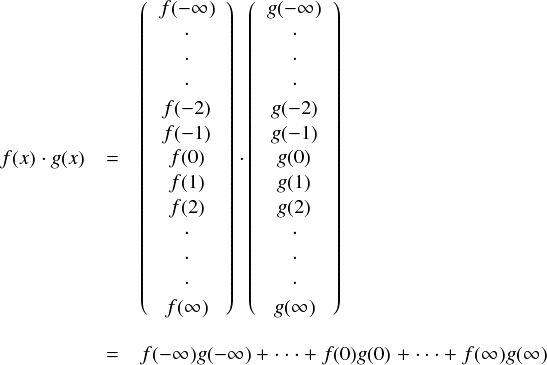
・・・という具合になります。ここでも,見やすくするためにxの値は整数のみにしてありますが, 実際はxは非常に細かく,というか無限に細かく変化します。 よって,この内積の計算も無限に続くことになります。 これだと,かけ算と足し算を無限に繰り返す必要がありそうです。手計算で可能なのか・・・? ということが心配になったりします。
しかし,ちょっと落ち着いて f(x)・g(x)の式を見てみます。 「f(x)とg(x)を各xの値でかけ算して,それをどんどん足していく」という計算は単に「f(x)g(x)」という関数の積分なんですね。 これなら普通に手計算でもいけます。なんだか,非常にそれっぽい感じになってきました。実際のところ,本物の(?)教科書でもコレが「関数の内積」と定義されています。
記号の話ですが, 関数どうしの内積をベクトルと同じように“f(x)・g(x)”と書いても構いません。(分かりやすければ何でもいいと思います。。。) ただし,教科書によっては“< f(x), g(x) >”みたいに三角カッコ < > で囲むのが関数の内積を表す記号として使われたりします。一応,両方書いておきます。
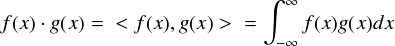
さてさて,やっと関数の内積を計算する方法が分かりました。
それで,本題は何だったかと言うと「三角関数が直交することを示したい」ということでした。 直交していることを示すには何を使えばいいのか・・・ ここまでの流れでは2次元ベクトルの話と完全に類似しているので,やはり2次元ベクトルと同じことをします。すなわち,「内積がゼロ」を示すことになります。
「内積がゼロ」というのは,「互いに共通な成分を一切持たない」ということでした。図形的に言えば直角です。だから「直交」という言葉が生まれたのでした。。。
しかし,関数のような無限次元ベクトルになった場合,もう図を書いてイメージすることはできません。関数どうしが直角で・・・とか言われても意味不明です。 それでも,「共通の成分を持っていない」ことは,2次元ベクトルと同様に「関数が直交している」と表現するようです。これは図形的な意味の「直交」を,さらに拡張した呼び方という感じです。 たとえ関数がらみの話だとしても,2次元ベクトルのイメージが効いてる言葉が出てきちゃったりします。 きっとそのほうが分かりやすいからなんでしょうけど。
次ページでは,とりあえず三角関数どうしの内積を計算してみます。積分するだけです。計算結果がゼロになることを期待しつつ。