トップページ > フーリエ変換入門(FFT入門) > 前フリ(2)
【遊び方】
説明が必要なほどたいそうな物ではありませんが・・・
右にあるスライドバーを上下にドラッグすると,sin関数がどんどん矩形波の形になったり,ならなかったりします。
作り方・ソースコードはFlash入門で説明しています。
スライドバーの位置に対応して,シグマの上の数字が変わります。その数字が,現在加算されているsin関数の総数となってます。(“N”の値) 1,2,3...とsin関数の数を増やすと,ジワジワと四角い波形になっていきます。

矩形波は,周波数が異なるsin関数をいくつも足し合わせて(重ね合わせて)作ることができます。 とりあえず,矩形波の関数を「 f(x) 」として,その中身がどうなってるのか書いておきます。
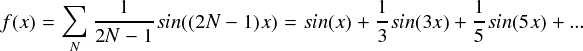
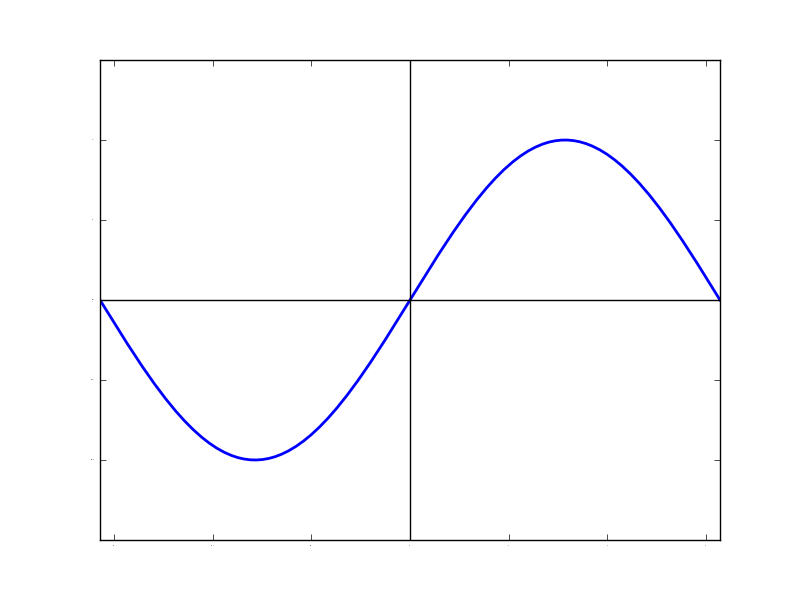
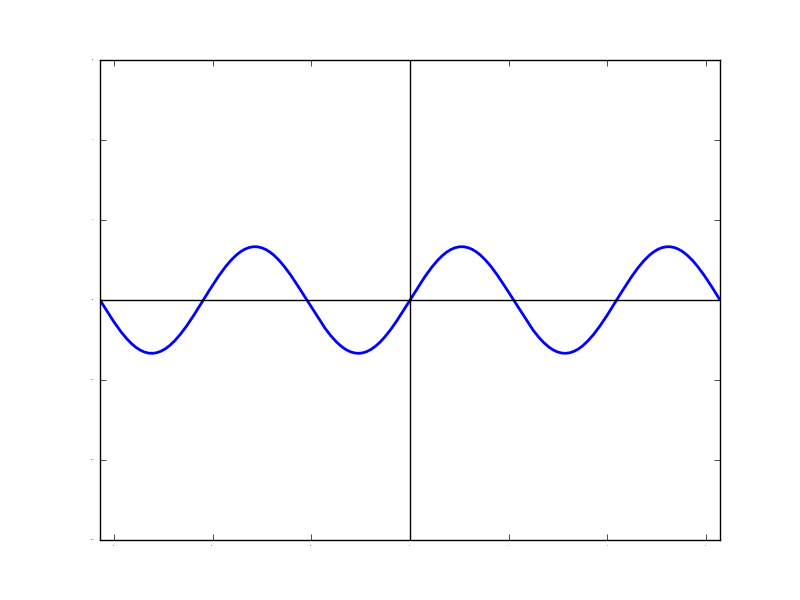
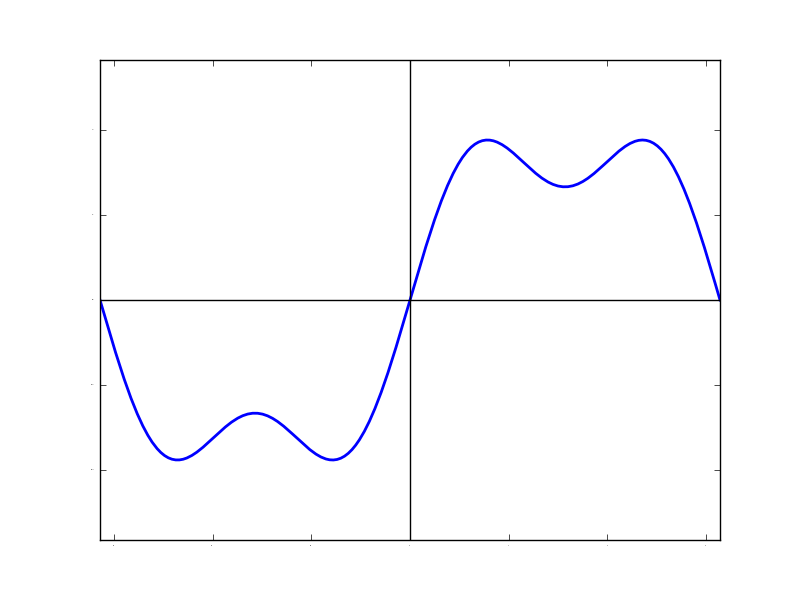
使うsin関数は周波数が(2N-1)となっています。(Nは整数)つまり,「周波数が奇数のsin関数」だけを足し合わせる必要があります。また,各sin関数の振幅は1/(2N-1)となっていて,「周波数が高いsin関数ほど小さい振幅」であることが分かります。 とりあえず最初のsin(x)と1/3・sin(3x)を足し合わせるというのが,どんな感じなのかを見てみます。 (冒頭のFlashのN=2の場合です)
| sin(x) | 1/3・sin(3x) | sin(x) + 1/3・sin(3x) | ||
|
+ |
|
= |
|
最初のsin(x)のピークのあたり(x=2/πとか)は,sin(3x)ではマイナスのピークとなっているため 相殺して四角い形に近づいていることが分かります。これがsin(5x),sin(7x)...と繰り返していくとどんどんピークの丸みが取れて四角くなっていきます。
最初のFlashでは,N=48が最大,つまり重ね合わせるsin関数の数は48個が最大となっています。 これをもっと大きい値にしたら,より矩形波に近づくのでは・・・? ということで,やってみます。
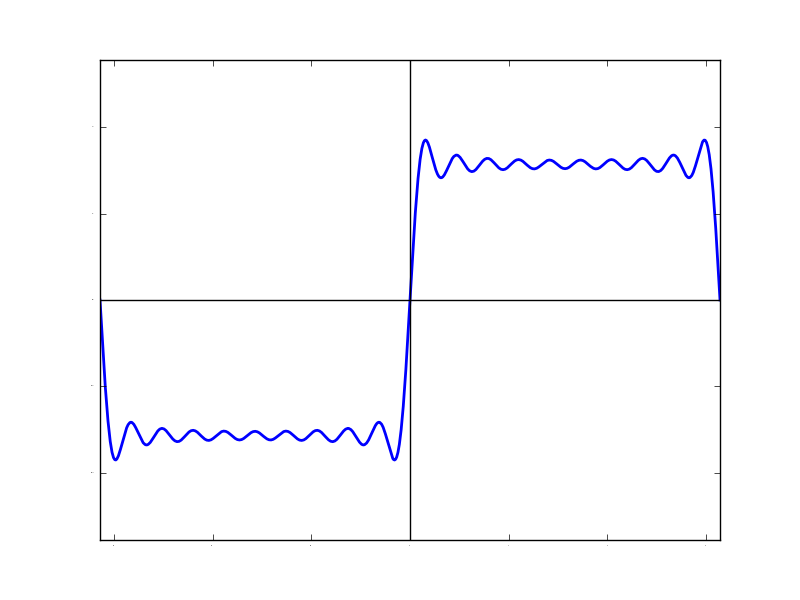
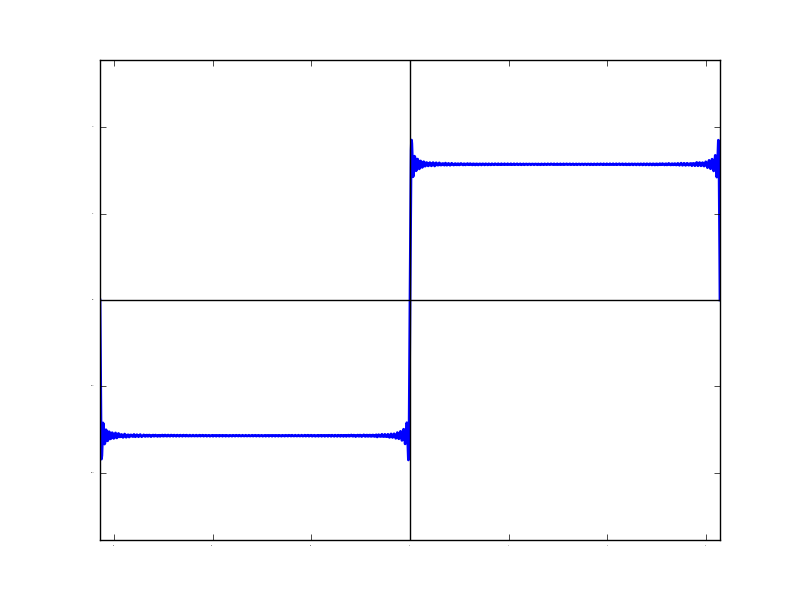
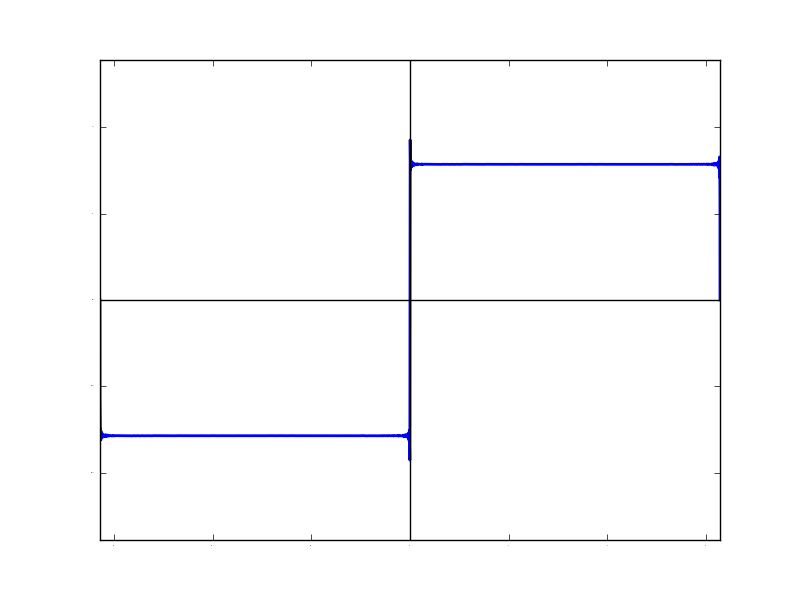
| N=10 | N=100 | N=1000 |
|
|
|
もうN=1000とかになると,ほとんど矩形波と呼んでいい波形です。こんなに角ばっているのに,その「成分」は全部sin関数なんですよね・・・ 不思議です。
矩形波に限らず,sin関数とcos関数の重ね合わせで他にも様々な関数を作ることができます。「まあ,ちょっとはそんな気がするかも」・・・という感じになってきました。
最初に「矩形波はこんな風にしてsin関数で作れる」と,下式を出しました。
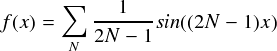
しかし,そもそもコレはどうやって導いたのか?という事が気になります。その方法さえ分かれば, 様々な関数を 「 sin と cos に分解する」ことができます。 これを説明するためには色々と準備が必要なので,後回しにします。。。
ここまでで,いろんな関数をsinとcosに分解できそうな気はしてきました。しかし,そんなことをやって何が嬉しいのでしょうか・・・? 上で矩形波を作るときには「周波数が異なるsin関数」をたくさん足し合わせていました。このことから,周波数が異なるsin関数は完全に「別モノ」というか,「別々のパーツ」というか,そんな気がしてきます。(あとから完全直交系の話で出てきます) しかも,ある関数をsinやcosに分解したときに出てくる「周波数の組み合わせ」は必ず関数ごとに「1パターンだけ」に定まります。これがすごく重要です。
では,何の役に立つのか。たとえば音声波形を相手にした場合,音声波形を1つの関数と見てsinとcosに分解すれば,「その音がどのような周波数の音を成分として持っているのか?」ということが分かります。言いかえれば,高音や低音がどのようにミックスされた音なのかという情報が得られます。オーディオ用スペクトル・アナライザは,まさにこの情報をLEDに表示させる回路です。
次ページ以降では「sin関数とcos関数だけで全ての関数を作れる」とは,どんな仕組みになっているのかを考えていきます。