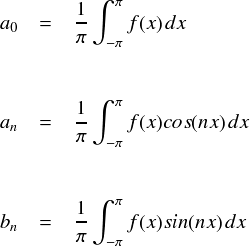
トップページ > フーリエ変換入門(FFT入門) > 収束定理(11)
ここまでの「収束定理」 の流れ全体を通して,フーリエ級数が収束すること, そして三角関数が完全直交系を張ることを確認してきました。
しかし,三角基底で様々な関数を表せるのは分かっていますが, その係数,すなわちフーリエ係数は最適な値を計算できているのでしょうか。。。
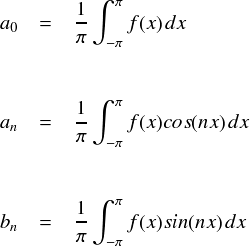
上のフーリエ係数の公式は, フーリエ係数のところで導出しました。 これをどうやって導出していたかというと, 「3次元ベクトルは基底と内積をとればその成分が出るから,関数もきっと同じノリでいけるはず・・・」 と,今思えばかなりテキトーな事をやっています。本当にこれで大丈夫なのでしょうか。
もし,ある関数をフーリエ級数で表すときに複数のパターンがあるならば, 当然,もともとの関数に一番近づくようにフーリエ係数を選びたいところです。 そんなわけで,あのフーリエ係数の公式で妥当なフーリエ係数を計算できているのかを確かめてみます。
たとえば,ある関数 f(x) を表すためにフーリエ級数を用意するとします。 そのフーリエ係数は,いつも通りの公式から出した値ではなく, 「別の値を持つフーリエ係数」だとします。 このフーリエ係数を, a'0,a'n,b'n と表わすことにします。
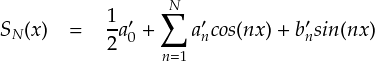
ここで, 「もともとの関数 f(x) と,フーリエ級数との差(誤差)を2乗して,1周期にわたって積分」 というのを考えます。 2乗しているのは誤差をすべて正の値としたいからで,1周期で積分しているのは 全体としての誤差を考慮するためです。 これを使って,関数とフーリエ級数の誤差を見積ることにします。
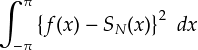
適当に計算を進めると,次式のような感じになります。
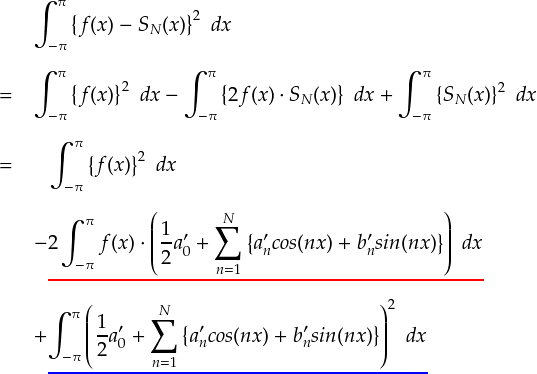
ちょっとゴチャゴチャしてきたので,1つ1つ分けて対処していきます。
まず,赤いアンダーラインの項ですが,これは 「フーリエ係数の公式」の形を利用して変形することができます。
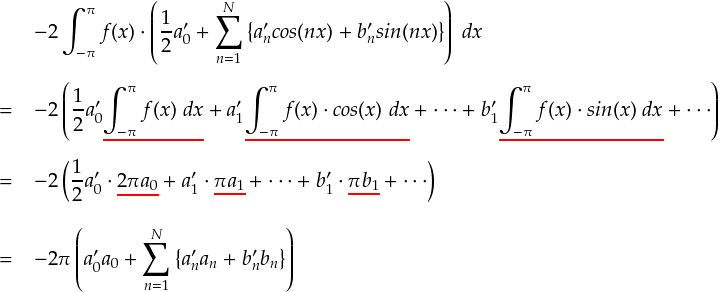
はい,これで式中に a'0,a'n,b'n の比較対照である本来の(?)フーリエ係数 a0,an,bn が出てきました。
次は,青色のアンダーラインのところです。
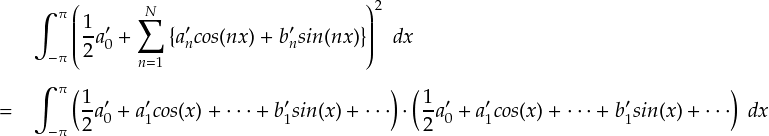
ここで,「三角関数の直交性」より,-π〜πの間で積分して残るのは自分自身の2乗だけとなります。 ( 三角関数の直交性(1) , 三角関数の直交性(2) 参照です。 )
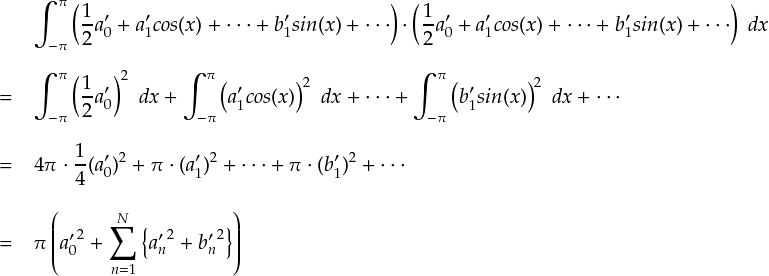
これで,赤いアンダーラインの部分と青いアンダーラインの部分を整理できました。 もう一度,最初から式を追ってみます。
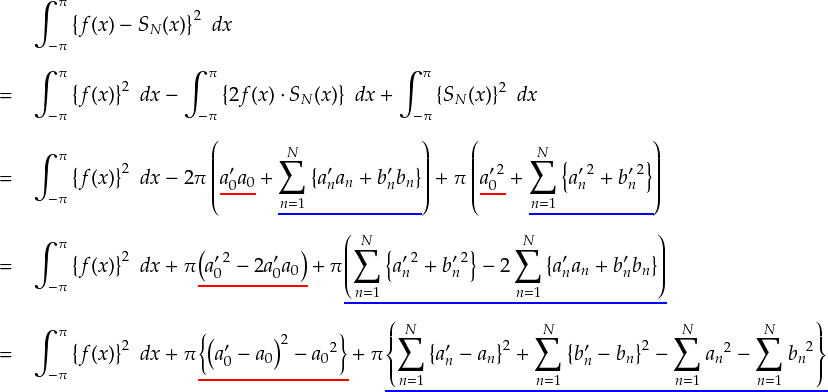
上式では,式変形の途中で「a - a'」のように2種類のフーリエ係数同士を引き算する形へ無理やりもっていっています。「比較」と言えば引き算(?)なので。
以上まとめると,もともとの関数とフーリエ係数の「二乗誤差」は次式のような関係になっています。
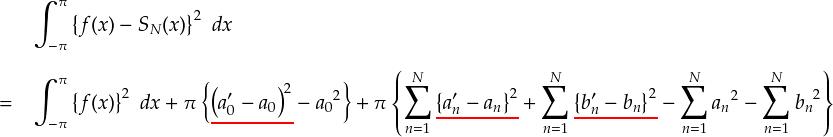
ここで,「二乗誤差」を最小にするのは赤いアンダーラインの部分がゼロになった時だと分かります。 すなわち, a'0 = a0 , a'n = an , b'n = bn が成り立つ時ということになります。 これによって,いままで使っていたフーリエ係数を導出する公式が 「最適近似」 となっていたことが確認できました。
このように,フーリエ係数は普通に公式で計算すればベストな値(?)となっているのですが, これを フーリエ係数は「極値性」を持っていると言うらしいです。
さらに,上式に a'0 = a0, a'n = an。 b'n = bn を代入してやります。
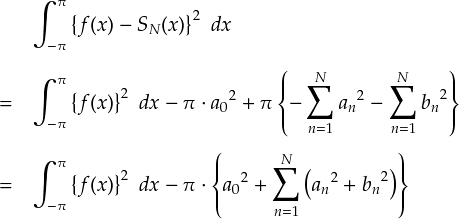
上式で「二乗誤差」の部分は,当然ゼロ以上となっています。よって,
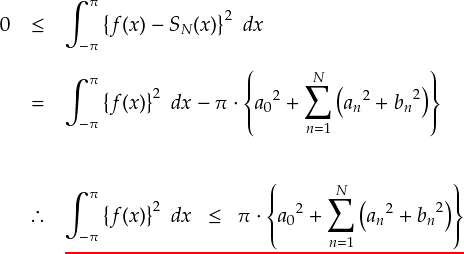
上でアンダーラインを引いた不等式を 「ベッセルの不等式」 (Bessel's inequality)と呼ぶそうです。
続けて,もう少しだけ式をいじります。 上の式において, N → ∞ の極限では SN(x) → f(x) となることを収束定理 のところで証明したので, 次のように式変形できます。
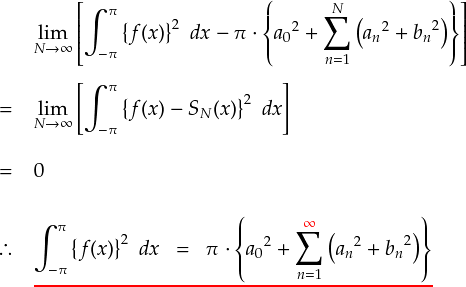
以上から, N → ∞ の極限ではベッセルの不等式の等号が成り立つことになります。 最後のアンダーラインを引いた等式を 「パーセバルの等式」 (Parseval's equation) と呼ぶそうです。
では,改めて「パーセバルの等式」を見てみます。
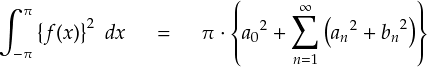
左辺の積分計算は,f(x) のノルムの2乗を求めるときの式となっています。 ノルムといえば,なんというか,関数をベクトルとしてイメージした場合の「ベクトルの長さ」 のようなものという感じです。。。
そして,左辺の方は各フーリエ係数を2乗して,全て足し合わせたような形になっています。 また,頭にπがかかっていますが,これは途中の三角関数の2乗を積分するあたりで出てきたのでした。 これは sin 関数や cos 関数のノルムの2乗である「π」であると考えられます。
そもそもフーリエ級数は「フーリエ係数×三角関数」という形式となっていました。 このフーリエ係数の各項のノルム2乗を計算したとすれば, フーリエ係数は定数なのでそのまま2乗されたものが出てきます。 sin関数や cos 関数の部分はノルム2乗としてπが出てきた・・・と見ることができます。 すると,パーセバルの式は 「f(x)のノルムの2乗」 = 「各基底関数のノルムの2乗の総和」 という式として見ることができます。 これは3次元ベクトルで言うところの3平方の定理に相当します。今回は無限次元なので,無限平方の定理というか,なんとうか。。。
ちなみに,パーセバルの等式に a0 = 0, an = 0, bn = 0 を代入すると, f(x) = 0 となります。 ここで,もしも三角関数以外の基底関数が存在するならば 三角関数の係数をゼロにしてもその基底が生き残るので必ずしも f(x) = 0 とはなりません。 よって,このパーセバルの定理によって前に証明した 三角関数の完全性 を再度確認できたことになります。