トップページ > フーリエ変換入門(FFT入門) > 収束定理(10)
前ページまでの収束定理の証明 で,もはや三角関数でできているフーリエ級数は(区分的なめらかな)様々な関数に収束することが分かっています。 既に「関数の基底」となるものは三角関数(と定数)で全部揃っている気がしますが。。。

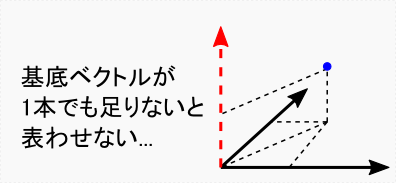
3次元ベクトルの場合で考えれば,基底ベクトルが1本でも欠けてしまうと, 「空間内の全ての点を表せる」とは言えなくなってしまいます。図ではz方向のベクトルが欠けているイメージですが, そうすると xy 平面内の点しか表わせず,表現できる位置が一気に少なくなってしまうことが分かります。 もし,この「基底が足りない」という事が3次元空間ならぬ「関数空間」で起こってしまうと, フーリエ級数は一気に実用性を失ってしまいます。
ダメ押しということで,とりあえず証明しておきます。
前フリと同じ感じで,「3次元ベクトルからの類推で・・・」などと考えたのですが, おなじみ(?)の背理法が一番てっとり早いので素直に背理法を使います。
最初に,(間違っているはずの) 仮定を次のようにします。
一応,「基底」っぽいということで “e(x)” という名前にしました。 この e(x) は sin や cos 以外の,「新しい基底関数」というイメージです。 上の仮定によれば,e(x) は sin関数,cos関数,定数と内積をとった場合にゼロになるはずです。よって,
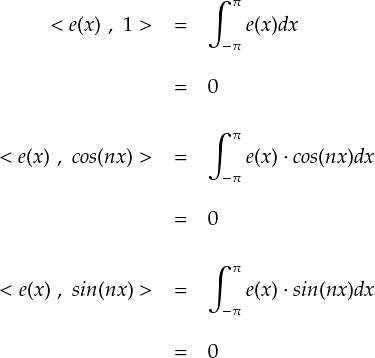
・・・という条件を満しています。ただし,nは整数です。 また,e(x) がどんな x においてもゼロとなるような関数でも上式は成り立ちますが, そんな関数は基底として役に立ちません。 よって, e(x) は常にゼロとなるような関数ではないとします。
ここで,e(x)とディリクレ核 との内積をとることを考えます。
突然ディリクレ核と内積をとるなんて突拍子もないことを言っているようですが, ディリクレ核の作り方(?)を再確認すると理由が見えてきます。
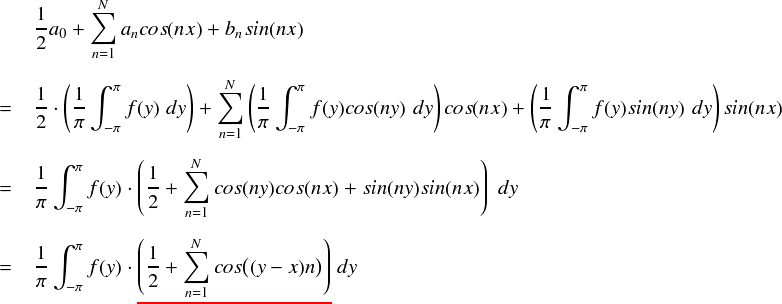
上式では,フーリエ級数からスタートして,最後に赤いアンダーラインを引いた部分がディリクレ核となっています。 すると,上式の最後の行は 関数 f(x) とディリクレ核で内積を取っているように見えます。
ここで,前ページの収束定理で示した通り, フーリエ級数は N → ∞ の極限でf(x)に一致するのでした。 (f(x)は変なエグい関数ではないとします)
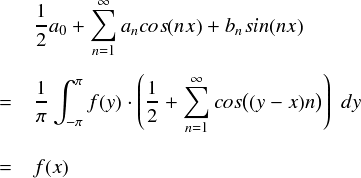
上式から分かることは,ディリクレ核には, 「ある関数 f(x) とディリクレ核との内積をとると, f(x) がそのまま出てくる」 という性質があるということです。 ディリクレ核のグラフは こんな感じでした。 アレと内積をとって f(x) がそのまま出てくるとは,ディリクレ核はいろいろ不思議ですね・・・。
それでは,本題の e(x) とディリクレ核で内積をとってみます。
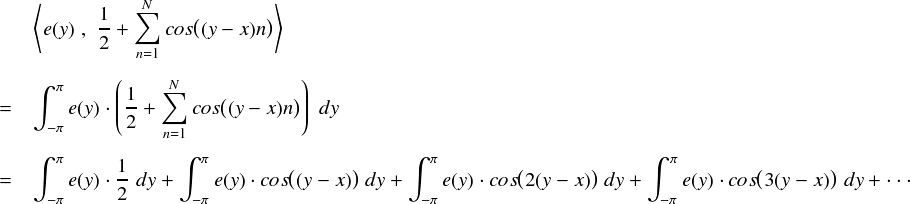
ここで,e(x) は最初の仮定で「e(x) は cos,sin,定数と直交する」としていたので, 各項の積分はゼロになります。
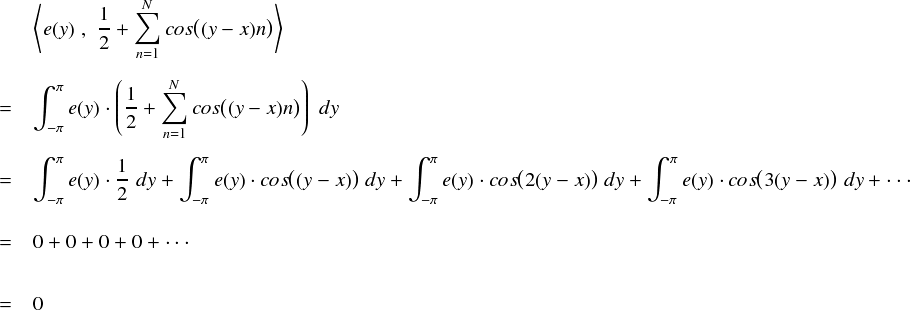
最初に,「 e(x) は常にゼロとなる関数ではない」と決めていたのに,内積計算の結果がゼロになってしまいました。。。これは,「 e(x)とディリクレ核との内積をとると,e(x) がそのまま出てくる」 というディリクレ核の性質と矛盾します。 それだったら,「 e(x) は常にゼロとなる関数だ」と決めてしまえば上式はディリクレ核の性質と矛盾しない気がします。 しかし,それはもはや「 e(x) なんて無い 」と言っているのと同じです。
以上から,「“関数の基底”となっているのは sin 関数, cos 関数, 定数 であり,これで全ての基底が揃っている」と言い切ることができます。
「sin関数,cos関数,定数」のセットは,完全に全ての基底を網羅していることが分かりました。 3次元空間が3本の「基底ベクトル」で全て表されるように, 「関数空間」はこの基底関数で全て表されることになります。 このように,その“空間”をすべて網羅するような基底を「完全性をもつ」 と言うそうです。
以上で,三角関数の性質に関する話は終わりです。 ここでは,いままで確かめてきた三角関数の性質を整理してみます。
まず,前フリの三角関数の直交性のところで, sin,cos,そして定数は全て互いに直交していることを確認しました。。
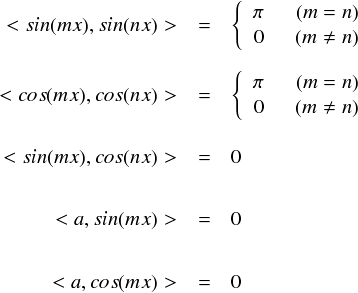
ここで,sin や cos は自分自身と内積を取ると計算結果がπになります。 2次元や3次元のベクトルでは,自分自身と内積をとると,そのベクトルの長さの2乗が出てきました。 よって,sin や cos の“長さ”の2乗がπなんだ,ということになります。 この「関数の“長さ”」のことをノルムと呼ぶのでした。 (前フリの中でも一応ノルムについて書いているところがあります。)
2次元や3次元の基底ベクトルは,普通に長さが1でした。 これは,当然「1」という長さが扱いやすいからです。よって,これに習って sin や cos の長さも「1」 にしてしまいます。別に難しいことは無く,ただ √π で割るだけです。 そうすればノルムが1になります。
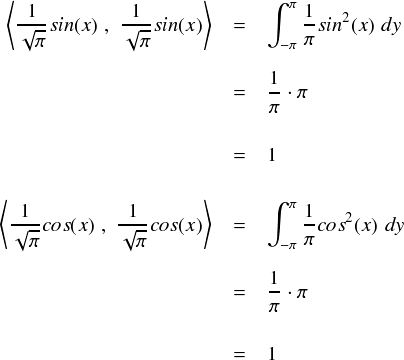
ただし,定数の基底の「1」は,自分自身と内積を取ると2πになっていました。 なので,こっちは √2π で割り算しておきます。これで定数の部分もノルムが1になります。
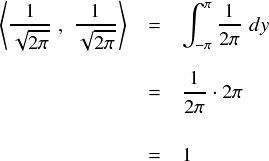
この,「ベクトルの長さ(関数のノルム)を 1 に揃える操作」を「規格化」 , もしくは「正規化」と呼ぶそうです。
ここで,いわゆる「関数の基底」を直観的に分かりやすくするために, 3次元の基底ベクトルと比較してみます。
| 3次元空間の基底ベクトル | 関数空間の基底ベクトル |
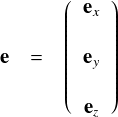
|
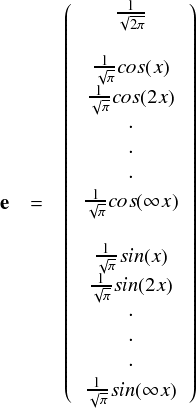
|
この sin,cos,定数から成る基底は「三角基底」と呼ばれているそうです。
以上のことを全部まとめると, このページで見てきたように,三角基底は完全性も持っているので, 「直交」していて,「規格化」されていて,「完全性」も満たすことになっています。 こういった基底のことを 「完全規格直交系」 もしくは 「完全正規直交系」などと呼ぶそうです。
また,2次元や3次元のベクトルでは,ベクトルが「面を張る」という言い方をすることがあります。
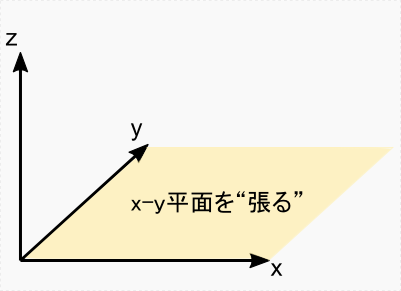
この言い方に習って,「三角基底は完全規格直交系を張る」 などと言うらしいです。
三角基底が完全規格直交系を張るということを聞くと, 量子力学で波動関数がどうのこうの・・・という話を類推してしまうのですが, それはまた「半導体入門」みたいな記事を書くときに出そうと思ってます。。。
次ページ以降は,おまけというか,おまけと言ったら失礼なのですが, これまでの証明結果から導かれる2つの公式を導出しておきます。