トップページ > フーリエ変換入門（FFT入門） > 収束定理（４）

ディリクレ核（２）

とりあえずグラフ

前ページでは，フーリエ部分和 S_N(x) をいろいろ整理していったところ，下式のようになったのでした。

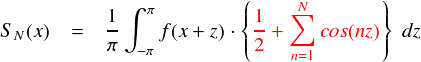
そして，S_N(x) の中に入っている級数の部分を「ディリクレ核」と呼ぶのでした。

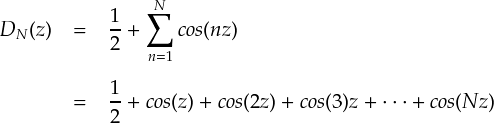
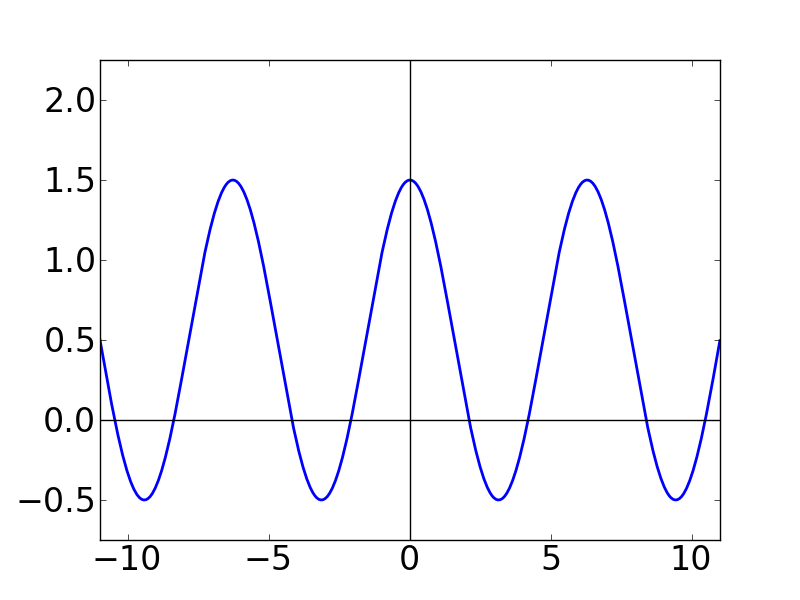
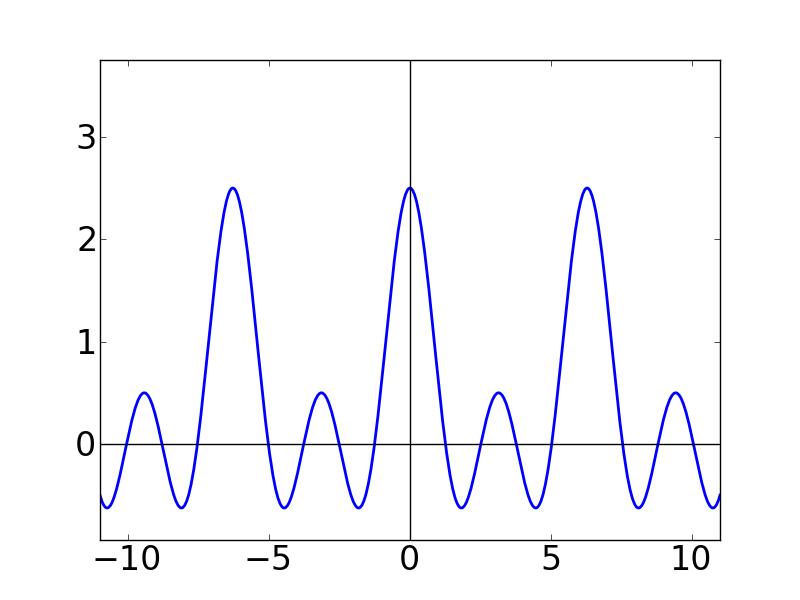
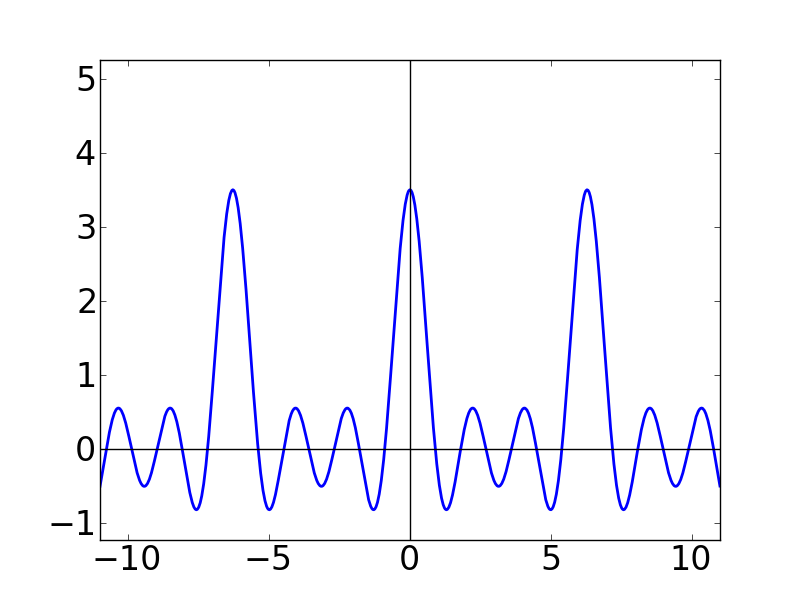
実際のところ，今の収束定理の証明の流れでは，ディリクレ核のグラフに大きな意味はありません。 でも一応，グラフを書いてどんなものか見ることにします。 例のごとく，Nの値をどんどん増やしていく感じにします。

N=1	N=2	N=3
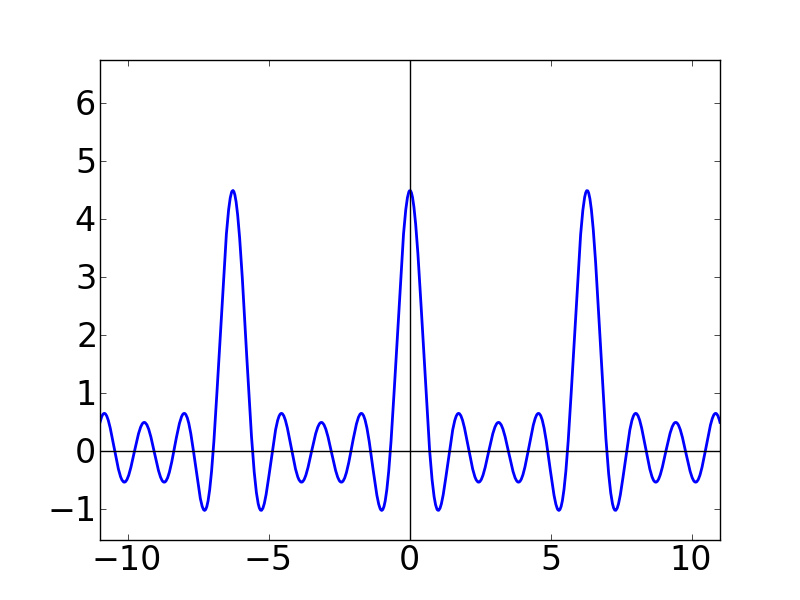
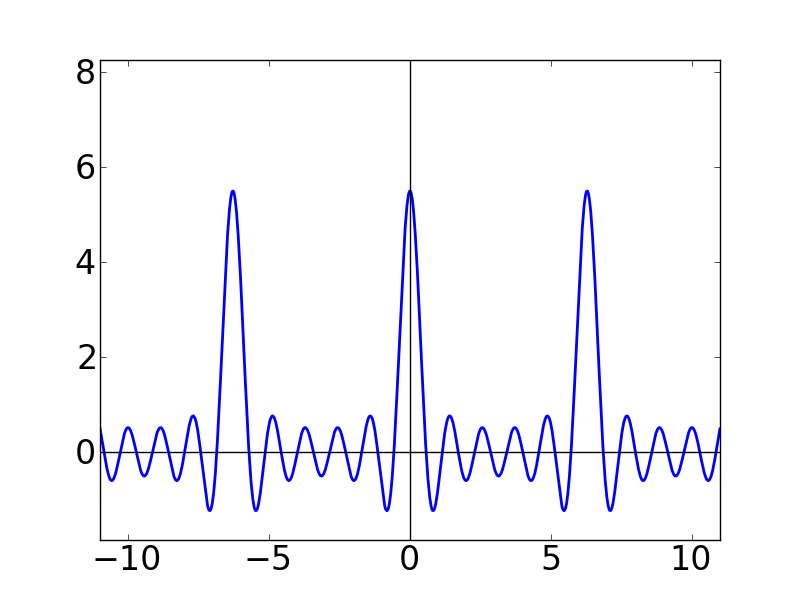
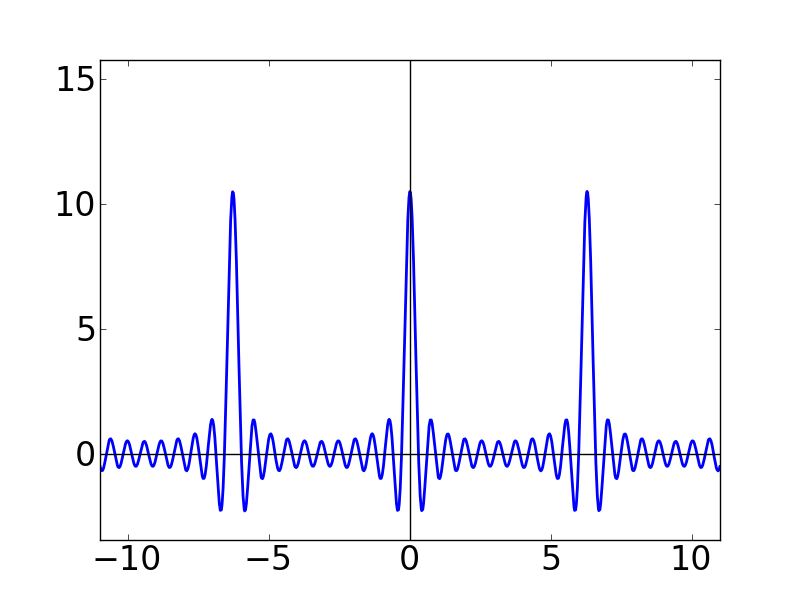
N=4	N=5	N=10
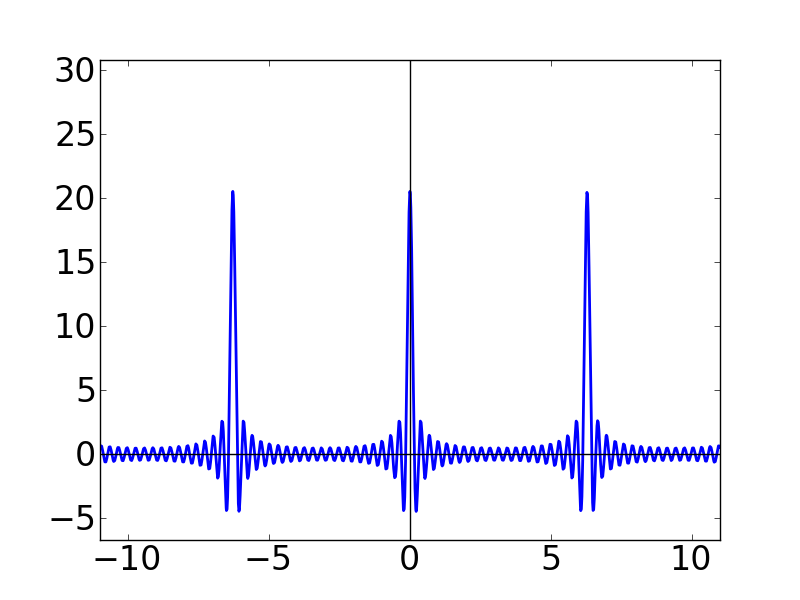
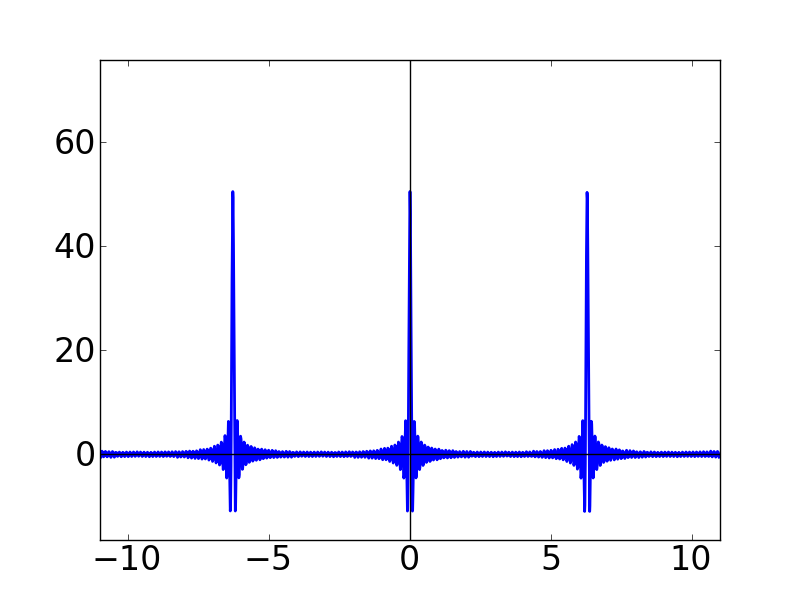
N=20	N=50	N=100

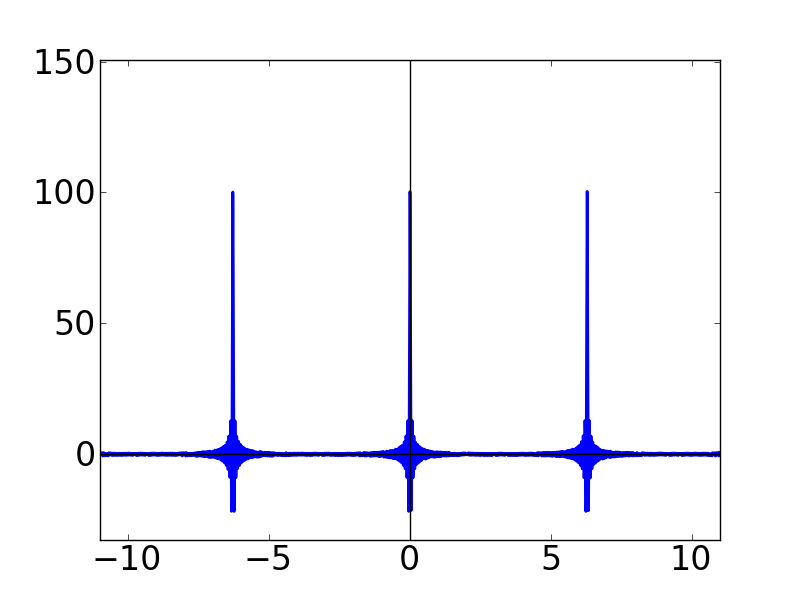Nの値が大きくなるにつれて，どんどん細くとがっていく感じになります。 また，各グラフの y軸を見ると，どんどん振幅（？）が大きくなっていることも分かります。 この関数はグラフの形から「くし型関数」とか呼ばれたりします。 　本名（？）は周期的デルタ関数という名前なのですが，これが後々（ずーっと後の離散フーリエ変換のところです）非常に重要になってきます。このディリクレ核は，ここでは言いきれないくらい使い道がある関数です。

本題に戻ります

それでは，最初にやりたかった「フーリエ級数は様々な関数と一致する」ことの証明に戻ります。証明したいのは次式でした。

上式を，S_N(x)の中身が分かるように書きなおしていきます。

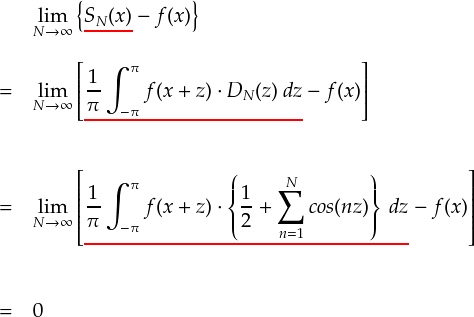
・・・これを証明したいわけです。 なんというか，積分の中にシグマが入っているというのが非常に扱いづらそうです。 等差数列や等比数列の場合は，シグマがついた総和を１つにまとめることができました。 今回もそんな感じでなんとかならないか，考えてみます。

ディリクレ核の中身をまとめる

ディリクレ核のシグマを，なんとか１つにまとめることを考えます。

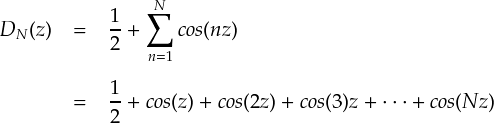
これはどう見ても等差数列には見えません。等比数列・・・でもないので，公比をかけて引き算して，，，みたいなことも無理そうです。「三角関数の級数」というのは，そもそも扱い慣れていません。

それでは，「三角関数の和をまとめる公式」ということで想像すると，一応「積和公式」というのがありました。 これは三角関数の直交性のところで使ったりしました。

加法定理から作るアレです。とりあえずsinバージョンを。

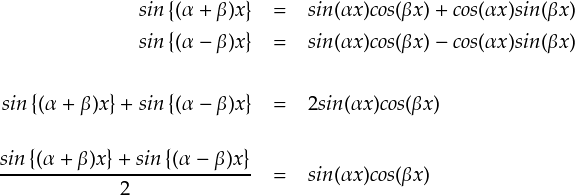
ディリクレ核の中身は全てcos関数でできています。ここにsin関数をかけてやれば，積→和で， さらにsin関数のみの足し算に変形できます。。。　天下り的な説明は嫌なのですが， ディリクレ核を扱う常套手段として「2sin(x/2)をかける」というのがあります。 昔の頭イイ人が思いついた方法みたいですから，素直に従っておくことにします。。。

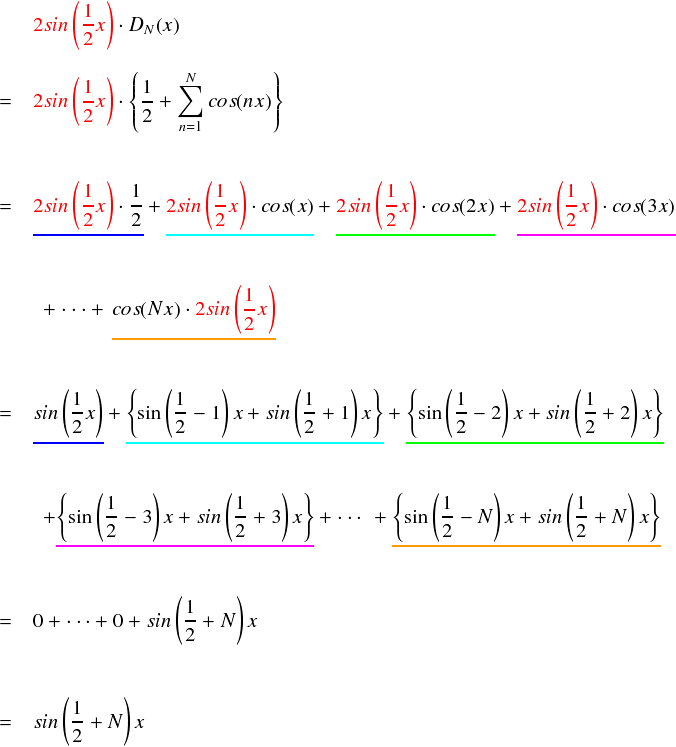
上式の途中で，sincos → sin + sin と変換すると，隣同士で符号が異なる項ができるので 相殺し合います。結局残るのは一番最後のsin(1/2 + N)x だけとなります。

そんなわけで，D_N(x) に 2sin(x/2)をかけた結果は次のようになっています。

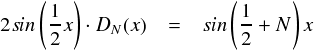
以上より，D_N(x) は次のようにまとまりました。

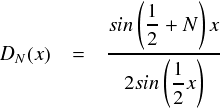
だいぶスッキリしてきました。。。では改めて，「証明したい式」に代入してみます。

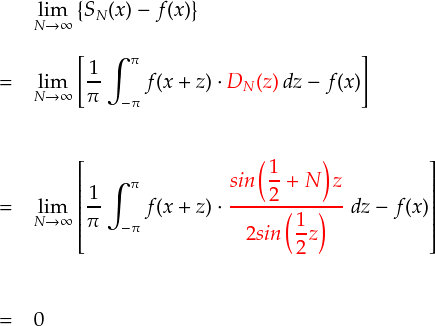
はい，こんな感じになってます。いろいろやりましたが，結局のところディリクレ核を整理するだけでした。 次ページでは，あまり手をつけていない f(x) の項の方をいじります。

前へ　 次へ