_f(x)_lim2.png)
トップページ > フーリエ変換入門(FFT入門) > 収束定理(5)
ここまでの流れを再度確認しておきます。 「フーリエ級数は様々な関数と一致する」ことを確認するために,下式を証明することを最終目標としているのでした。
_f(x)_lim2.png)
それで,前ページ・前々ページの中でいろいろあって,結局下の式まで変形してきた,というところです。
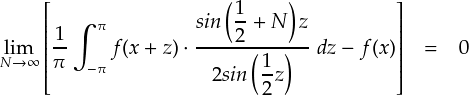
積分の中に入っているディリクレ核がなんとも扱いづらい雰囲気です。 実際のところ,ディリクレ核だけを-π〜πで積分したらどうなるのでしょうか? ちょっとやってみます。
ただし,あのsin関数山盛りの部分はそのままだと積分する時に扱いづらいので, 今回だけcos関数の和の形に戻してしまいます。
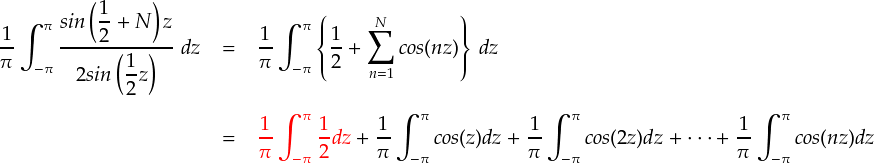
ここで,cos関数はcos(x)だろうと,cos(2x)だろうと,-π〜πで積分すれば全てゼロになります。 よって,この中で残るのは赤色の1/2を積分する項だけとなります。
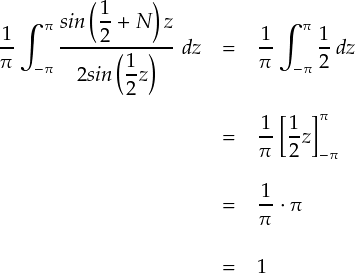
・・・ということで,以外とあっさり片付きました。しかも,ディリクレ核の積分結果は「1」です。 なんというか,あんなにゴチャゴチャした関数なのに,きれいな数字が出てきて不思議です。
それでは,この結果を使って更に式変形を続けます。
上で求まった結果は次の通りです。
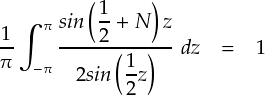
この関係を,最初の式に代入していきます。
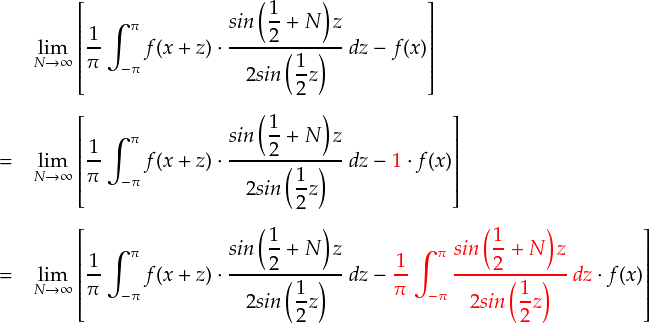
ここで,「x」という変数は外部から与えられるものとなっています。 「フーリエ級数がどんな場所でも関数f(x)と一致する」ことを確認するために,単に「x」という変数で自由度を持たせているにすぎません。要は,「x は固定値だと見なすことができる」ということです。 なので,当然「f(x)」の値も定数となっています。
f(x) が定数なので,インテグラルの外と内を自由に出し入れすることができます。 (f(x+z)は,zという積分変数が含まれているため定数ではありません)
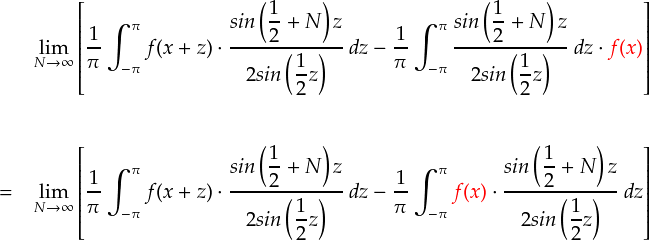
なんだか共通因数でくくれる雰囲気になってきました。続けて変形していきます。
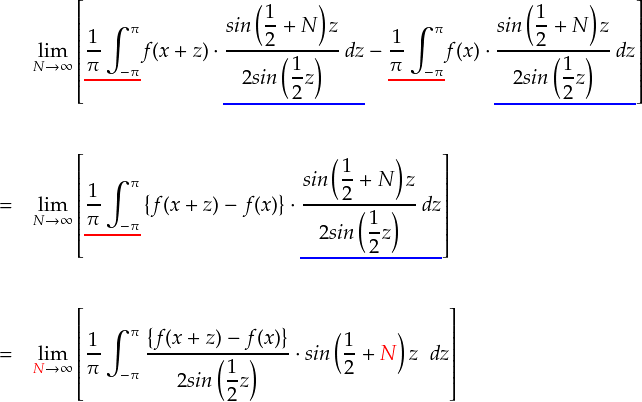
ディリクレ核に関わる変形は,これで終了となります。 ここから先に進むには,もう一発「リーマン・ルベーグの定理」というのが必要なので, 次ページではその話に進みます。