トップページ > フーリエ変換入門(FFT入門) > 収束定理(6)
前ページ までの結果として,今,「フーリエ級数が様々な関数 f(x) と一致する」 ことを示すために証明したい数式は,次式のようになっています。
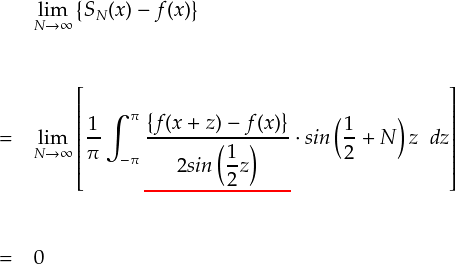
複雑そうに見える式ですが,少しずつほぐしていきます。
まず,赤線を引いた部分には極限に関わる「N」が含まれていません。 さらに,いま考えている数式では,「“x”という変数は一時的に固定されている」と考えても構わないのでした。 積分変数「z」が動くのに対して,xは定数とみなすことができるということになります。 よって,赤線を引いた部分は単純に「z」だけの関数と見なすことができます。
そんなわけで,赤線を引いた部分を,「よく分からないけど z の関数だ」という意味で「g(z)」と書いてしまいます。
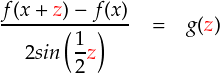
最初の式を,g(z)を使って書くと次のようになります。ここから,これを証明する流れとなります。
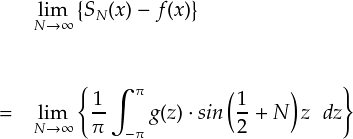
上式では,もはや変数は z だけです。わざわざ「z」なんて慣れない文字を使う必要は無くなりました。 そんなわけで,積分変数を「x」にしておきます。
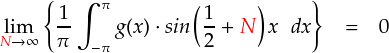
はい。とりあえず,見かけは単純になりました。次は,上式がどんなイメージの極限になるのかを見ておきます。
上で最後に出てきた式では,「適当な関数 g(x) × 周波数が(1/2+N) のsin関数」 というブロックが-π〜πで積分されています。 それで,いま証明したいのは,「sin関数の周波数Nがどんどん大きくなると, 積分した値がゼロになる」,ということです。 正直なところ,数式だけ見てもピンときません。。。
ここで,「g(x) × sin(1/2+N)x 」はどんな様子なのかをグラフで見てみます。 g(x)は今回の特別な関数ではなく,ますは分かりやすい例でやってみます。 とりあえず,単純に「 g(x) = x 」という1次関数でいきます。
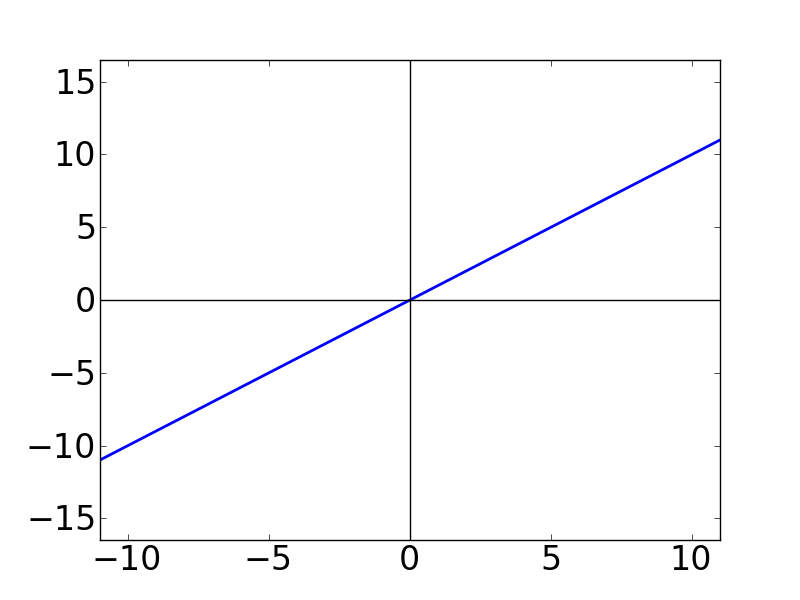
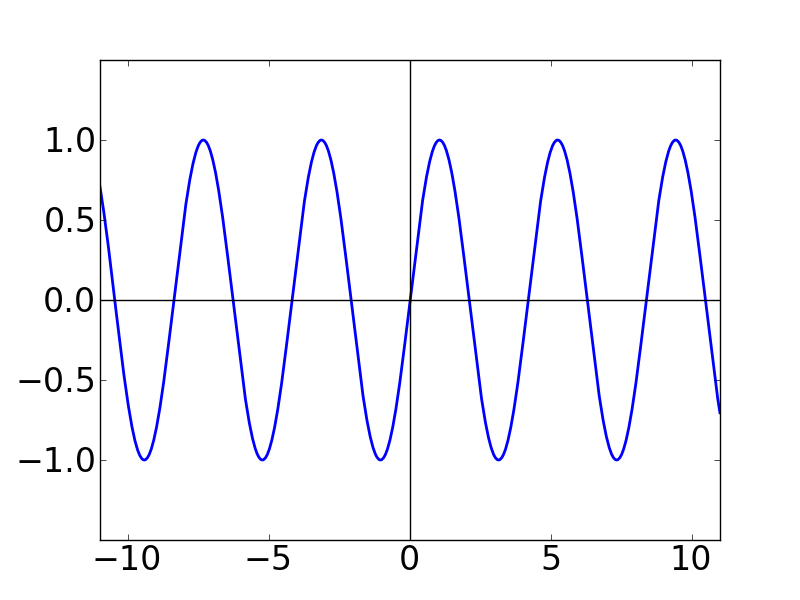
左から順に,「g(x)」のグラフ( 要は y = x のグラフです),「sin(1/2 + N)x」のグラフ, そして一番右がこの2つの関数をかけ算したものとなっています。
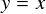 |
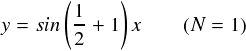 |
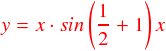 |
 |
 |
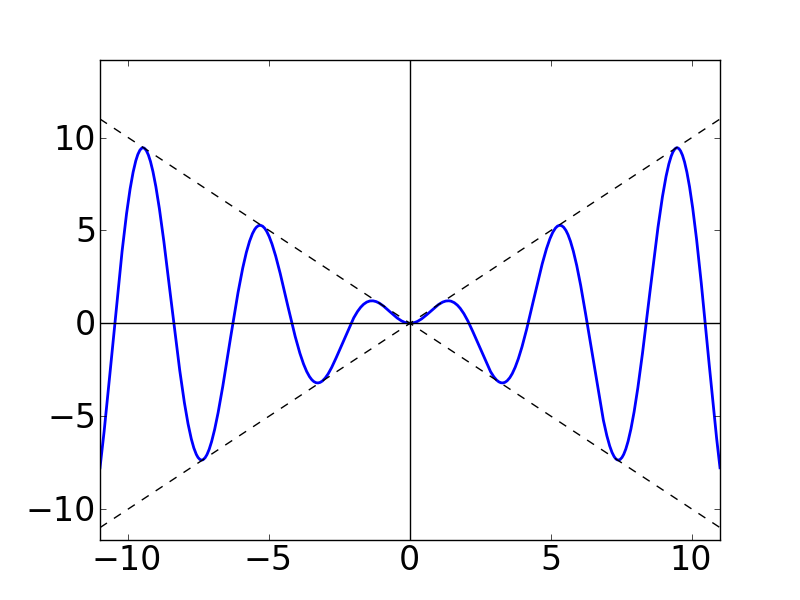 |
一番右側のグラフの形は,sin関数の振幅が g(x)によって変調されている・・・という感じです。 点線は y = x のラインを表しています。 今回は N = 1 のグラフを描いているわけですが,まあどう見ても-π〜πで積分してゼロになるとは思えません。 あくまでパッと見た感じ,というだけですが。。。
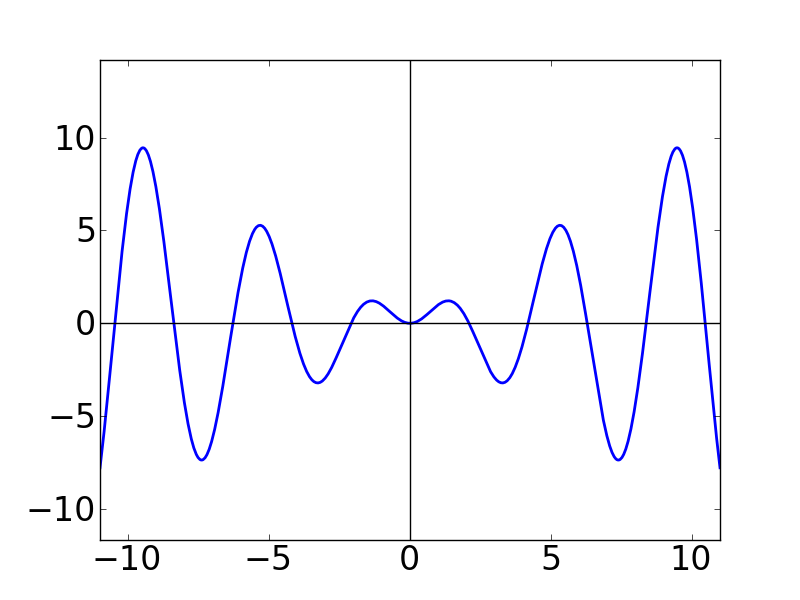
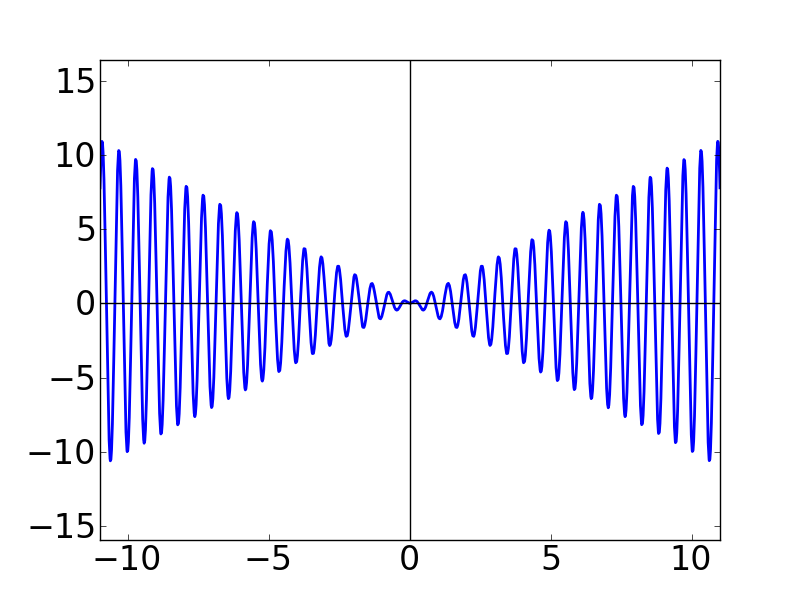
それでは, N の値を大きくしていくとどうなるでしょうか。例のごとく,どんどん並べていきます。 N はsin関数の周波数なので,Nを大きくすればどんどん波形は細かくなっていくのですが・・・
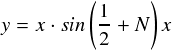 |
||
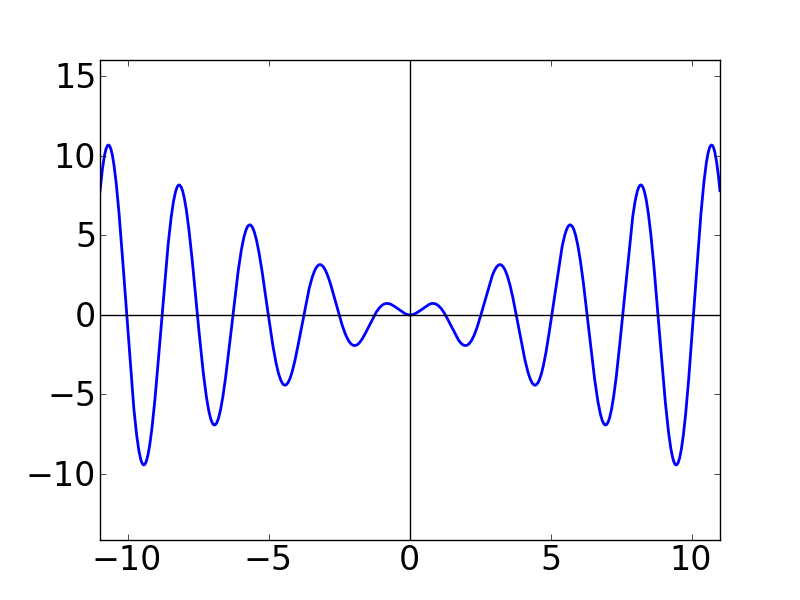
| N=1 | N=2 | N=3 |
 |
 |
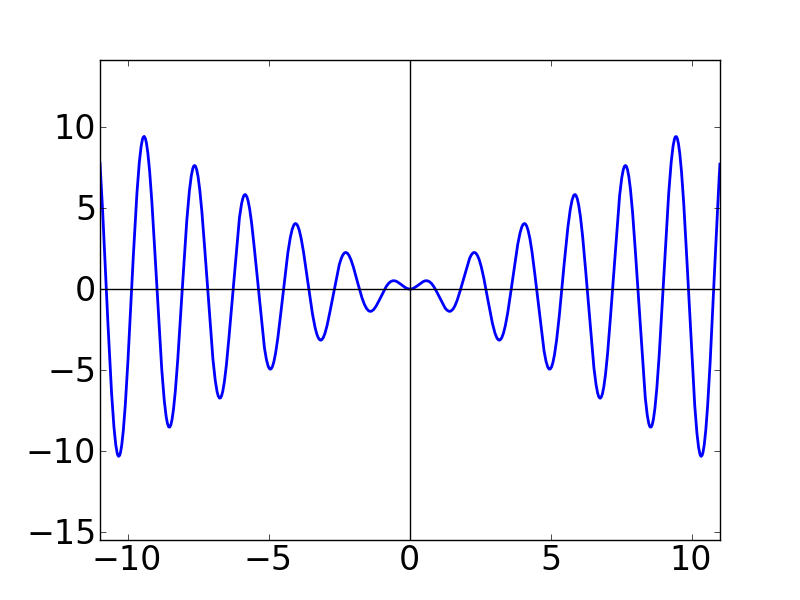 |
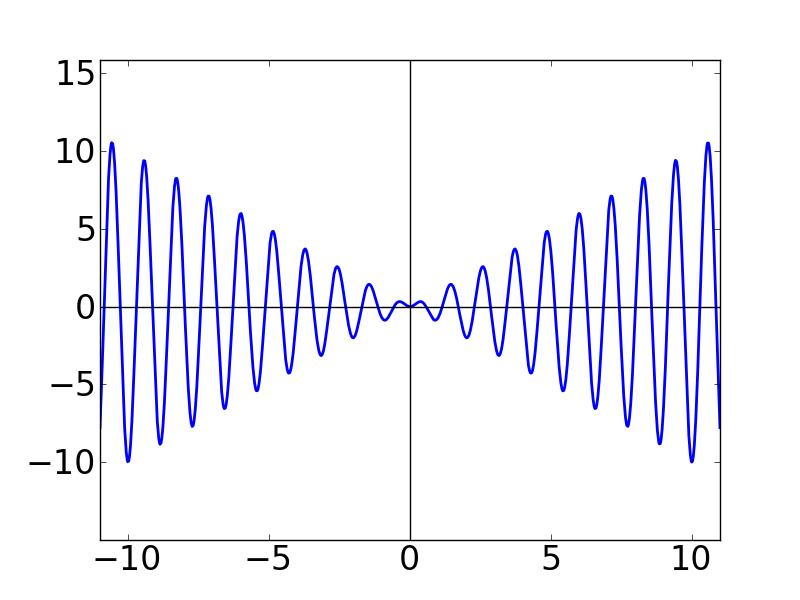
| N=5 | N=10 | N=20 |
 |
 |
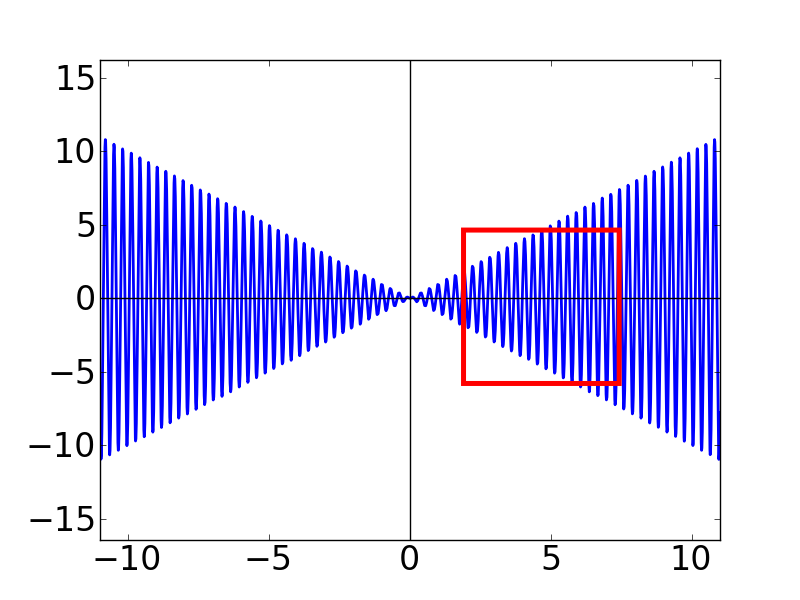 |
上のグラフのうち,N = 20 のグラフに赤い四角を書きました。 ちょっとこの部分を中を拡大してみます。
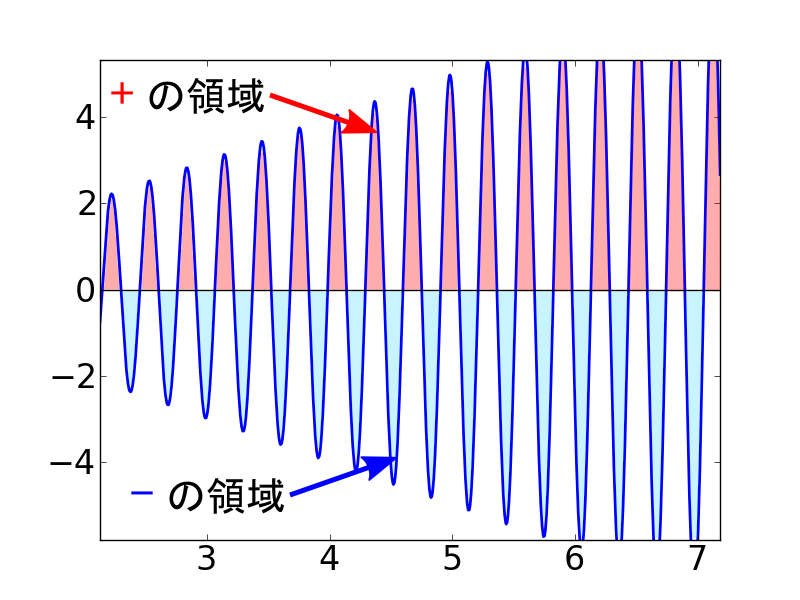
sin関数が十分細かくなると,上半分(正の領域)と下半分(負の領域)がほとんど同じ面積 になっています。もし,N → ∞ とすれば「上下の面積は完全に等しい」と言い切れる雰囲気です。 そうすると,プラスの部分とマイナスの部分の面積が相殺するので,最終的に積分値はゼロになります。
いまイメージを作ったのは以下の式でした。
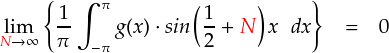
実際,最終的にゼロに収束するのは,係数の1/π が無くても同じです。 また,積分区間はこれまでの流れから「-π〜π」としていましたが, 別に積分区間をどう取っても「正の領域と負の領域が相殺して消える」ことは変わりません。 たとえば,積分区間を適当な文字「a」と「b」で指定しても構わないことになります。 さらに,sin関数の周波数 N はどうせ無限大に飛ばすので,sin関数の中の“1/2”は極限を取る時に無視できるという感じです。
以上をふまえて,上式のエッセンスを取り出すと次のようになります。
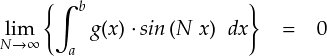
だいぶスッキリしました。 この関係式は「リーマン・ルベーグの定理」 (Riemann-Lebesgue lemma ) ,もしくは「リーマン・ルベーグの補題」とか呼ばれているそうです。リーマンさん(1826 - 1866) と,ルベーグさん (1875 - 1941) は, フーリエさんより後の人達みたいです。。。
さて,リーマン・ルベーグの定理について,一応イメージ上はそれっぽい雰囲気だと分かりました。 しかし,絵を見て考えただけなので,ちゃんと数式で証明しておく必要があります。
ところで,そもそも何故こんな話の流れになったかというと,最初のモチベーションは次式を証明することだったのでした。
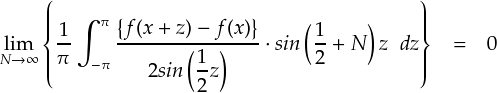
上の式を証明できれば,「フーリエ級数と様々な関数は一致する」ことを数式で証明したことになるのでした。 (いろいろと間が長くて初期目標を見失いそうですが,ココから始まった話です。) それで,上式を良く見ると,まさにリーマン・ルベーグの定理のパターンに当てはまることが分かります。 よって,リーマン・ルベーグの定理をきちんと証明しておくことは,フーリエ級数の収束をきちんと証明する上で 重要になってきます。
次ページでは,とりあえずこの「リーマン・ルベーグの定理」を数式で証明することをやってみます。