トップページ > フーリエ変換入門(FFT入門) > 収束定理(7)
前ページ で出てきた「リーマン・ルベーグの定理」は,下式のような感じでした。 “適当な関数とsin(Nx)の積を積分したもの“ において N → ∞ とするとゼロに収束する・・・という定理です。 これをきちんと証明しておかないと,フーリエ級数の収束の話が進みません。
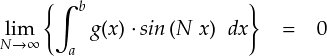
前ページではディリクレ核がらみのゴチャゴチャしていた部分をまとめて,「g(x)」と書いていました。 しかし,今回の目的である「リーマン・ルベーグの定理の証明」は一般の関数をイメージして構いません。 それならば,普通に「f(x)」と書いた方が良いですよね。。。
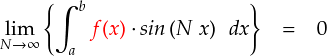
g(x) と書いていたものを f(x) と書き直しただけです。このほうが見やすいので・・・
それで,上式は 「関数 f(x) とsin関数の積の積分」なので, 例のごとく部分積分のパターンになってます。ちょっと計算を進めてみます。
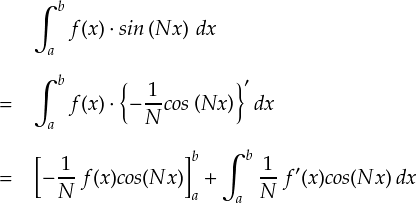
この計算結果において,N を無限大に飛ばしてみます。 各項には 1/N という係数がかかっているので, N → ∞ でゼロに収束します。 それに対して,cos関数の中にも N が入っていますが,いくら N が大きくなっても結局 cos関数の値は -1〜1の範囲 に収まっているので,トータルでゼロに収束することには変わりありません。
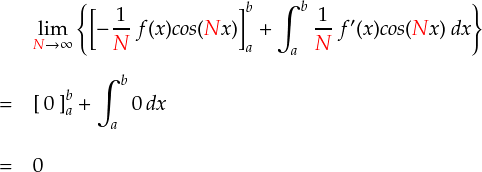
意外とあっさりですね,,,と言いたいところですが,大きな見落としがあります。
もし, f(x) や f'(x) が無限大 だとしたら,いくら N が無限大になったとしても ∞ / ∞ の形の不定型になってしまいます。 よって,この定理を成り立たせるためには f(x) にいろいろ制限を付ける必要があります。
まずは,f(x) が無限大に発散しては困ります。
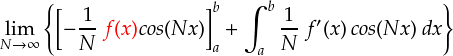
分母の N が無限大になった時にトータルでゼロになって欲しいわけです。 よって,f(x) は無限大だと困るのですが,ある値さえ持っていればいくら大きくても問題ありません。
そんなわけで,適当に大きな数字 “M” を使って f(x) を縛っておきます。 (この手の話では必ず“M” が使われます。何故かは知りません・・・ Max 的なものだと思います)
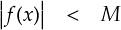
よって, tan(x) みたいな関数は無限大に発散する点を持っているので,この定理を満たさないことになります。
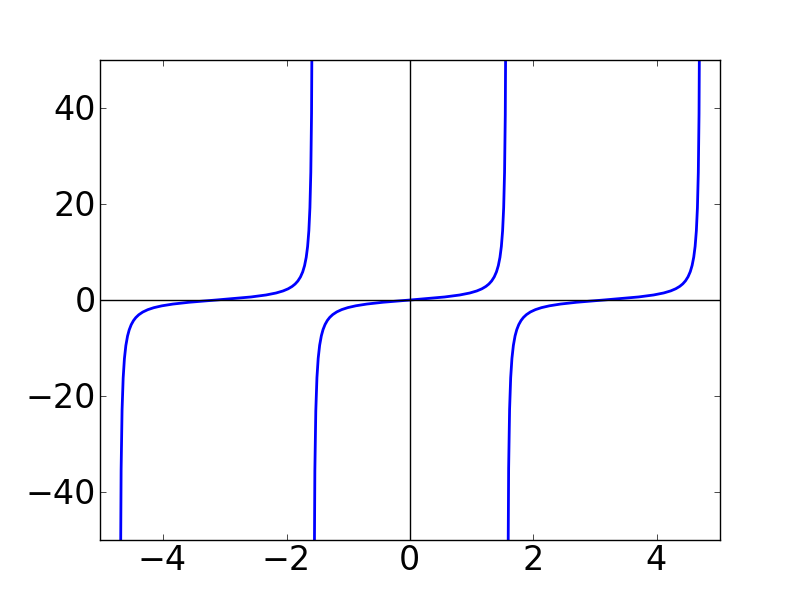
かといって,tanと同じようにブツブツ途切れていても( = 不連続でも),振幅が有限値の矩形波ならば条件を満たします。 実際,不連続関数だとしても有限でさえあれば「区分求積法」が使えるので積分計算はできそうな感じです。
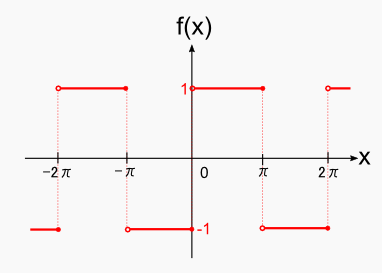
以上から,連続・不連続に限らず,「無限大に発散する点を持たない」ことが大事だと分かります。 これを数式で表すと,不連続点の端を a,b として,
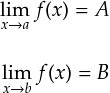
という感じで,それぞれの片側極限値 A と B が存在すれば良いということになります。 もちろん,A と B は何か適当な値で,無限大であってはダメです。
上の矩形波で片側極限を求めてみます。とりあえず連続区間の1つ 0 < x ≦ 1 を選んでやると,
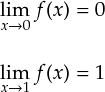
となって,片側極限は両方とも有限値だと確認できます。 まあ,グラフから見たまんまの結果ですけど。。。
不連続点はいくらあっても良いのですが(無限個あると困りますけど),とりあえず各不連続点で片側極限が存在すれば, 一応当初の条件は満たされる感じになっています。
この,「各不連続点で片側極限値が存在する」という条件を「区分的に連続」 と呼ぶそうです。「連続」という言葉を使っているのですが,直感的には単に「関数が無限大に発散しない」というイメージで良いんじゃないかと思います。。。
次は,f ' (x) も無限大に発散しては困るという話です。
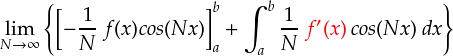
ここまでの流れでは,「不連続関数でも全然OK」という感じなので,微分を計算するときも不連続関数を相手に計算するイメージでいきます。
さっきと同じ感じで,ある関数が a < x < b で連続で,x = a と x = b で途切れているとします。その時の a, b での微分係数は次の極限計算で求まります。
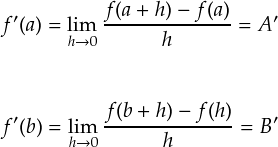
f ' (a) の値はA' ,f ' (b) の値はB' になる感じで書いてます。このA' と B' が無限大でなければ良いわけです。 このように,不連続関数の中にある連続区間の両ハジにおいて, 「微分係数が発散しない」ことを「区分的なめらか」と呼ぶそうです。 「なめらか」という言葉は微分がらみで出てくることが多いので,なんとなく覚えやすいかもしれません。。。 (※ この「区分的なめらか」という言葉は「区分的微分可能」と呼ばれることもあるみたいです。)
ここで,そもそも f(x) 自体が発散していたら,微分係数の計算結果も発散します。よって,「区分的なめらか」であるためには,「区分的連続」であることが必要となります。
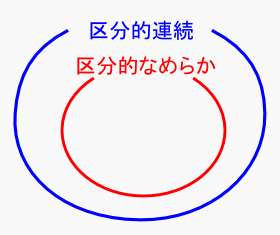
フーリエ解析の教科書には,区分的連続とか区分的なめらかの話が出てきます。 これはリーマン・ルベーグの定理に必要,もっと言えばフーリエ級数の収束に必要ということになってます。
次ページでは,リーマン・ルベーグの定理が「区分的連続」という条件だけでも成立するのか 確認します。