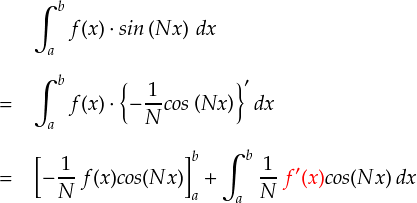
トップページ > フーリエ変換入門(FFT入門) > 収束定理(8)
前ページの最後では, リーマン・ルベーグの定理が成り立つための条件として,f ' (x) が有限でないと困るという話でした。
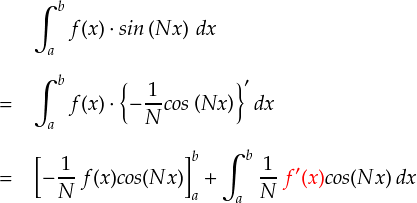
しかし,f ' (x) が発散してしまう矩形波でも,フーリエ級数展開できることが分かっています。
(矩形波のフーリエ級数展開のところです。)
なんだかよくわからないので,
とりあえず前ページで確認済みの「区分的なめらかな関数では,リーマン・ルベーグの定理は成り立つ」
ことを頼りに,証明を続けてみることにします。
まずは,ベースとなる連続関数の「f(x)」を考えておきます。f(x)は無限大に発散する点を持たないものとします。 この条件を数式で書けば,下式のようになります。 (一応。)
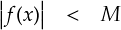
ここで出てきた「 M 」は適当な数で,f(x) の大きさを縛るものです。(無限大に発散しない,ということが言いたいだけです。) 絶対値が付いているのは,負方向の振幅(?)が最大かもしれないからです。 このf(x)は発散しない連続関数としているので,当然,「区分的なめらか」の性質を満たします。 以上の性質を備えた f(x) なら,リーマン・ルベーグの定理を満たすことが分かっています。 そんなわけで,この f(x) は今後の話の土台となります。
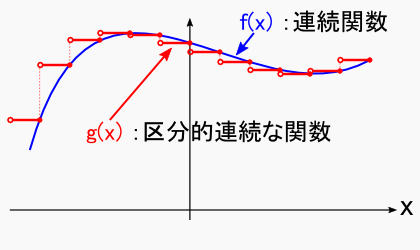
次に,上で定義した f(x) に似せて,「区分的連続」な関数の「g(x)」を用意します。 この g(x) がリーマン・ルベーグの定理を満たすことを証明するのが今回の目的です。 g(x) は区分的連続( = 不連続な点を含む)なので,ガタガタした形になってます。 それでも,g(x)の値の範囲は元にしている f(x) と同じように値の範囲を縛ることができるはずです。
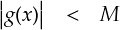
それでは,この g(x) を積分することを考えます。
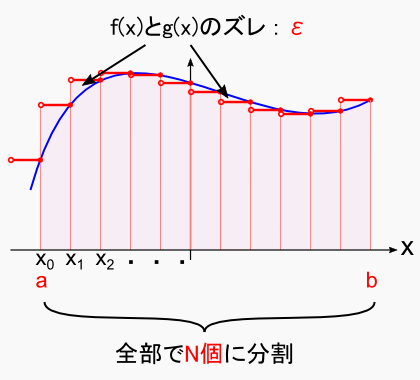
g(x)のような不連続関数を積分する時は,“連続な区間ごとのブロック”でそれぞれ積分し,最後にブロック全体を足し合わせる というのが常套手段です。「区分求積法」とか「リーマン和」とか呼ばれているやつです。(高校数学で普通に習う「積分」です)
この“連続な区間ごとのブロック”を指定するために,数列でおなじみ(?)の「適当な整数 i」を使うことにします。 ここでは,“i 番目の連続な区間”を xi 〜 xi+1 の間とします。 また,ブロックの数は全部で N 個あるものとします。 すると,この関数の積分は次式のような感じになります。
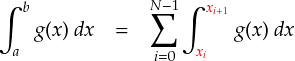
このとき,グラフから分かるように,f(x)とg(x)の面積の間にはズレが生じてしまいます。 このズレは f(x) と g(x) の誤差が原因となっています。 この誤差を「ε」(イプシロン)と書くと,次式のような表現ができます。
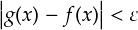
「f(x) と g(x) の間の誤差は,一番大きくても ε 以内に収まる」という感じの式です。 この手の話ではよく ε が使われます。何故かは知りません。。。 きっと昔のえらい人が考えたんだと思います。
今の図だと g(x) の1つ1つのブロックの幅が大きいのでガタガダです。εの値もけっこう大きい感じです。 しかし, g(x) をどんどん細かくしていけば ( = 分割数 N を大きくすれば) g(x)がきれいに f(x) の形にフィットして敷き詰められる(?)感じになります。 すなわち,誤差 ε は ,N → ∞ の極限で ε → 0 となる と,直観的には分かります。 (ここらへんの話は“微積分学”とかの話になります。細かい証明はその方面の教科書でどうぞ。これを書きだすとまた膨大な量になりそうなので。。。)
とりあえず, | g(x) - f(x) | の値は g(x) が不連続でも ,分割数を細かくしていけば限りなくゼロにできる,というのが重要です。 それだったら「区分的連続」な関数でもリーマン・ルベーグの定理が成り立つ気がするのですが。。。 次で詰めます。
それでは,改めて今証明したい式を出しておきます。
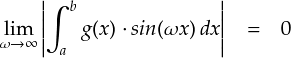
くどいですが,g(x) は「区分的連続な関数」です。前ページのストレートな式変形ではこれがゼロに収束することは示せませんでした。 また,sin関数の中で,xの係数を「ω」に変えています。
これは,ここまでの話の流れで「g(x)のブロック数」にN を使ってしまったからです。
正直,いままでの“ sin(Nx) ”というのは若干違和感がありまして,「あの N は角振動数 ω と書いた方が分かりやすいかな・・・」と思っていた次第であります。。。 そんなわけで,今更ωに変えました。
(※当初なぜ N を使ったかというと,ディリクレ核の中身を整理するところで
cosの項数が「 N 個」というのがあって,その流れを引きずっていたのでした )
それでは,上の式のままでは扱いづらいので,先ほど出てきた “| g(x) - f(x) | ”を利用しやすいように無理やり変形します。
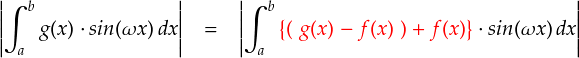
はい。無理やり “ g(x) - f(x) ” を作って,あとから f(x) を足すことで±0 にしてます。 今のところ,「積分値の絶対値」をとっている式になっていますが, 「先に関数の絶対値を取って積分する」ほうが大きい値になります。 (関数が負の値を取るところでも正の値で積分されるので。) これを利用して不等式を作っていきます。
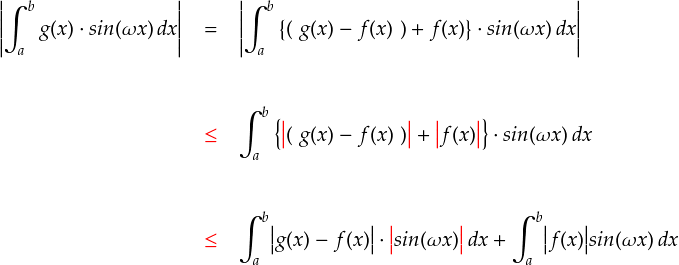
ここで,欲しかった“ | g(x) - f(x) | ”の形が出てきました。この部分は「ε」より小さいという条件を付けていましたので,これを使って更に不等式を進めます。
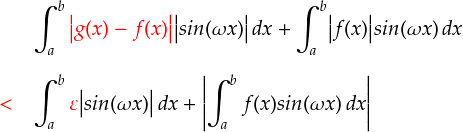
sin関数は -1〜1の間の数をとるので, | sin(ωx) | は必ず1以下です。 これも取り入れます。
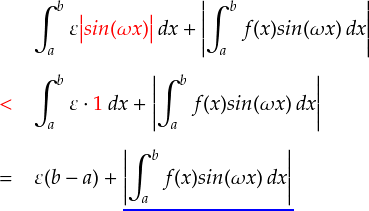
さて,g(x)の分割数次第で, ε → 0 となることは前に見ました。 さらに,積分区間の a や b というのは適当な定数なので,結局第一項のε( b - a ) というのは ゼロに収束します。
さらに,第二項の積分されているブロックは,まさに連続関数 f(x) に対する リーマン・ルベーグの定理そのものになっています。。。ということで, ω → ∞ とすれば第二項もゼロに収束します。 以上合わせて, N → ∞ と, ω → ∞ とすれば以下の極限が成り立ちます。
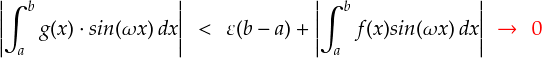
そんなわけで,区分的連続な関数 g(x) でもリーマン・ルベーグの定理が成り立つことが証明できました。。。 重かったです。
さてさて,やたら長かったですが,以下の「リーマン・ルベーグの定理」を証明できました。
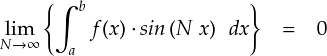
このリーマンルベーグの定理は,関数とcos関数の積のパターンもあります。 そちらも N → ∞ の極限でゼロに収束します。(証明はsinの時と同じ流れなので省きます) ここで,この定理を満たす関数 f(x) の条件をもう一度確認すると, 「関数が区分的連続であること」 ということでした。 「区分的なめらか」は,区分的連続も含みますので十分条件ということになります。 そして,「区分的連続」の実際のイメージは「関数が有界であること」,すなわち 「関数が無限大に発散しないこと」という感じでした。
この定理の積分のところをよく見ると,見覚えがある形だと気づきます。
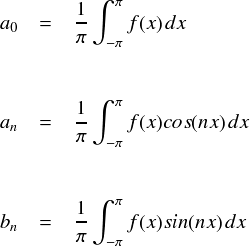
上に出したのは,「フーリエ係数」を計算するための式です。 関数と sin または cos をかけ算して,ある区間で積分・・・というのがそっくりです。 実際のところ,リーマン・ルベーグの定理の積分区間 a ,b は適当に定めてよい定数だったので -π〜πとしてしまえば完全に同じです。。。
すると,リーマン・ルベーグの定理の言いたいことは, 「 sin や cos 関数の周波数が無限大のとき,様々な関数でフーリエ係数はゼロになる」 もしくは,「様々な関数は,周波数が無限大の成分を持たない」 ということになります。 ・・・まあ確かに,直観的に考えて関数がものすごく速い,というか無限大の 周波数の成分を持っているというのは考えづらいです。実のところ,このリーマン・ルベーグの定理が証明できたことは,フーリエ級数の収束を示したのと同値となっています。 しかし,途中の話の1発1発がやたらと重かったので, 次ページではもう一度整理して,頭からフーリエ級数の収束について流れを見なおしてみます。