トップページ > フーリエ変換入門(FFT入門) > フーリエ級数(4)
前回までで,フーリエ級数とフーリエ係数についての話は終わりです。 いままでの内容を使って,前フリ で出てきた矩形波をフーリエ級数に展開します。

「矩形波」は,おそらくクロックパルスのイメージでおなじみだと思います。 実際の電気信号であれば,パルスの立ち上がり・立ち下がりはつながっていて波形はなまっています。 今回は理想的な矩形波ということなので,立ち上がりや立ち下がりは瞬時に可能なものとします。
数学でいう「関数」として扱うためには,「1つのxで複数のf(x)が存在してはならない」という関数そのものの定義を意識しておく必要があります。そんなわけで, 1つの区間の中では上の図のように上下がかぶらないようにしています。-π〜πの1区間で言えば,下のような感じになります。
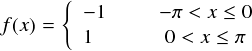
前に書いたように,今のところフーリエ級数は周期2πの周期関数しか表現できないので,今回の矩形波も周期2πに設定しておきます。そんなわけで,全ての領域における 今回の「矩形波関数」は次式のようになります。(nは整数です)
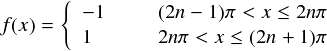
それでは,この矩形波関数をフーリエ級数で表したときの,フーリエ係数を計算してみます。 前ページでa0,an,bnをそれぞれ求めるための公式を作りましたので, 今回もそれぞれを計算します。必要な積分計算は3回ということになります。
a0を求める式は以下の通りでした。
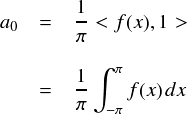
ただ-π〜πで積分して,πで割り残するだけです。。。今回の矩形波では-π<x≦0と,0<x≦πで値が違うので,積分するときは2つに分けて計算します。
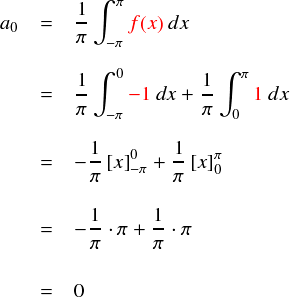
a0はゼロになりました。そもそも,a0というのはその関数の1周期における平均みたいなイメージだったので,1と−1に振れている矩形波のa0がゼロになるのは当然という感じです。
次はcos関数の係数となるanを計算します。anの計算式は次式でした。
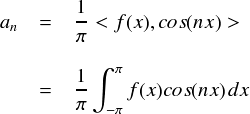
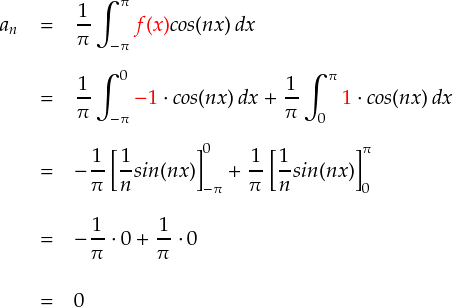
最後はsin関数の係数であるbnです。bnの計算式は次式となっていました。
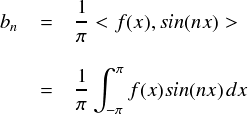
例のごとく,代入してダラダラ計算します。
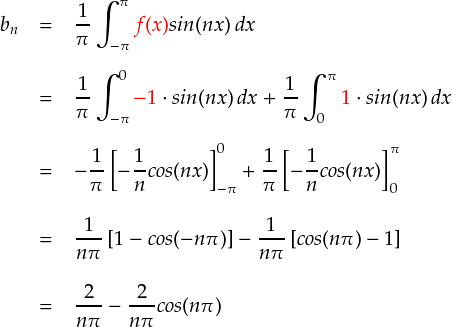
ここで,場合分けが必要になります。cos(nπ)というのは,nが奇数の場合に「-1」となり, nが偶数なら「1」になります。すなわち,nが偶数か奇数かで,上式の最後が「4/nπ」になるか「0」になるかが決まります。
そんなわけで,新しく自然数の「m」というのを用意して,奇数であれば「2m-1」,偶数であれば「2m」と書くようにしてしまいます。
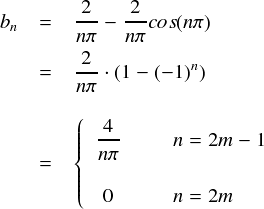
今求めたいのは「bn」,つまりsin(nx)の係数でした。 それなのにbnの値が,別の文字である「m」で書かれている・・・というのは分かりづらいです。 よって,bの添え字に合わせて書きなおしておきます。 要は,奇数だけが残ればいいので,次式のようになります。
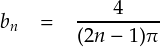
上の式は,分母に「2n-1」が入っていることで,どんなnだったとしても分母は奇数になるようになっています。 このほうがスマートです。
全ての矩形波のフーリエ係数が揃いました。で,あとは各フーリエ係数に上で求めた 「a0 = 0」,「an = 0」,「bn = 4/(2n-1)π」を代入するだけです。 ただし,sin関数のフーリエ係数は偶数でゼロだったので,sin関数の周波数は奇数のみということになります。
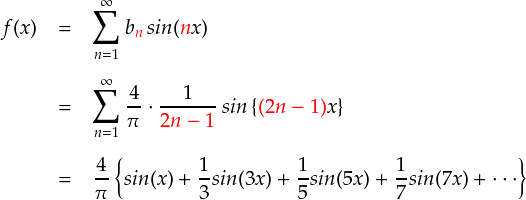
上の式が,前フリで使った式ということになります。 全体にかかっている「4/π」は,単に矩形波の「高さ」を決めているだけです。 前フリでは,sin関数の重ね合わせで矩形波でも再現できることを示したかったので, 最初の4/πを抜いた必要最低限の項でやったという感じです。