トップページ > フーリエ変換入門(FFT入門) > フーリエ級数(5)
矩形波だけというのもさびしいので,下のような「三角波」もフーリエ級数にバラしてみます。 また,まとめとして,最後の方でフーリエ級数展開を手計算でやるときに計算量を減らす方法についても触れます。

これを「関数」として表現すると,次式のようになります。区間は周期関数っぽく-π〜πで定義しておきます。 これが隣の区間でも延々と続く感じになります。
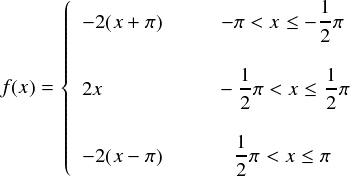
グラフの通り,今回例にとった三角波は基本的に「傾きが±2の直線」で構成されています。
-π〜-π/2の区間では「y = -2x」の直線を右方向へ(x軸負方向へ)πだけスライドしたものとなっています。(x切片が-πなので) よって,平行移動を取りいれて「y = -2(x + π)」です。 -π/2〜π/2の区間では,原点を通ってるのでそのまんま「y = 2x」。 π/2〜πの区間では,「y = 2x」の直線を左方向へ(x軸正方向へ)πだけスライドしたものなので,「y = 2(x - π)」としています。
フーリエ係数を計算する際は別に難しいことはなく,単に積分するときの積分区間を,この関数の切れ目ごとに分割していくだけです。
それでは,前回と同じ手順でフーリエ係数を取り出していきます。
前回と同じ感じで正攻法で計算すると非常に面倒だ,というデモということで。
(フーリエ係数を求める公式の導出は 「フーリエ係数」でやってます。)
a0を求める式は以下の通りでした。
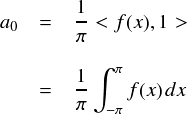
f(x)に,上で定義した三角波を入れて計算していきます。
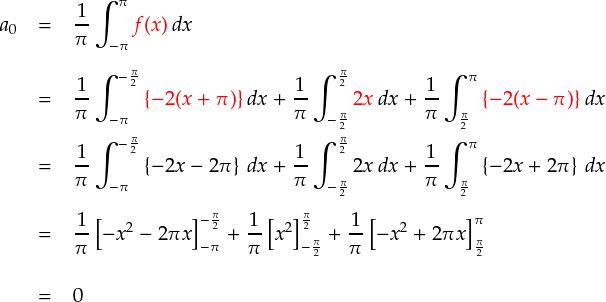
・・・ということで,a0 = 0 になりました。原点を通る波形はオフセットが無いという感じで, a0がゼロになります。
次はanです。一応公式を出しておきます。
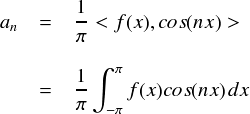
実際に計算していきます。
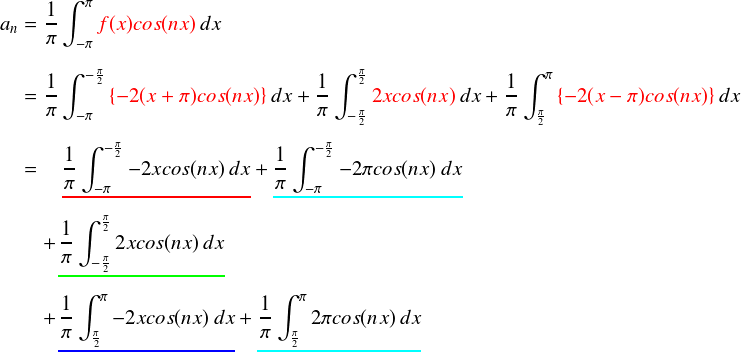
f(x)を代入してほぐすと,「xcos(x)」型の積分計算が出てきました。部分積分の典型です。 赤・緑・青のそれぞれを部分積分の公式を使ってほぐしていきます。
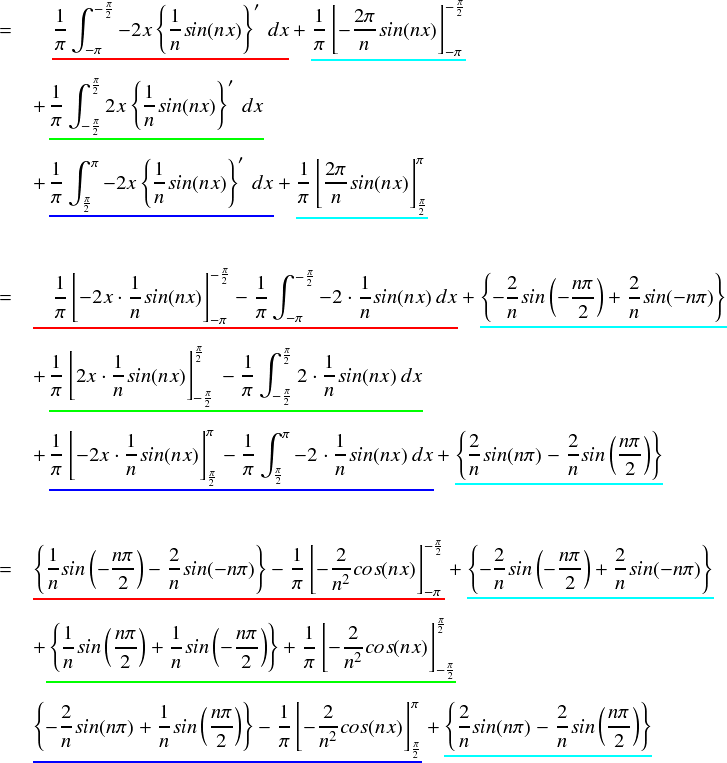
ここで,水色の部分は符号が逆同士なので消えます。また,赤・緑・青の最初の{ }の中もうまく符号が合わさってゼロになります。 なお,「sin(nπ) = 0 (nは任意の整数)」と, 「sin(-x) = -sin(x)」を利用しています。
よって,最後に残るのは赤・緑・青それぞれの[ ]の部分だけとなります。
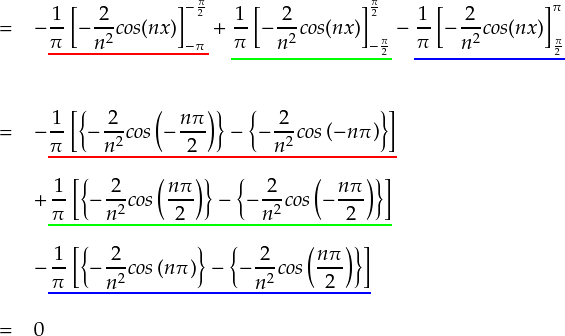
・・・ということで,うまい具合にゼロになりました。ここでは,「cos(-x) = cos(x)」という関係を利用しています。 こんなに計算したのに,結局ゼロなんですね。。。
後でもっと楽できる方法を考えます。
最後にbnを求めます。
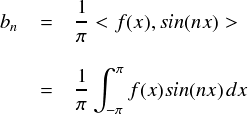
実際に計算します。f(x)を代入した後の流れはanの時と同じような感じです。
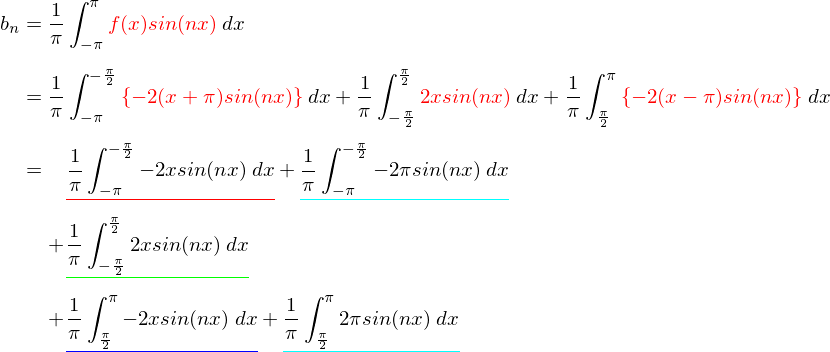
今度は「xsin(x)」型の積分が出てきました。これも前と同じように部分積分でほぐしていきます。
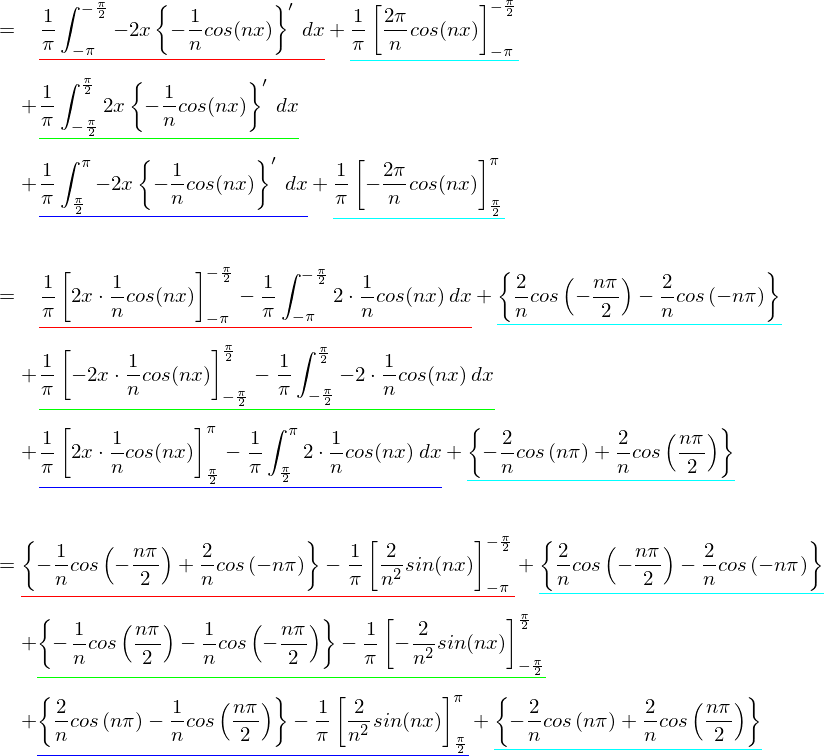
上式において,赤・緑・青・水色の部分に含まれる{ }の中は,トータルでゼロになります。 その結果,結局[ ]の項だけが残ります。 なお,ここでも「cos(-x) = cos(x)」の関係を使っています。
そんなわけで,最後に残った部分だけ計算していきます。
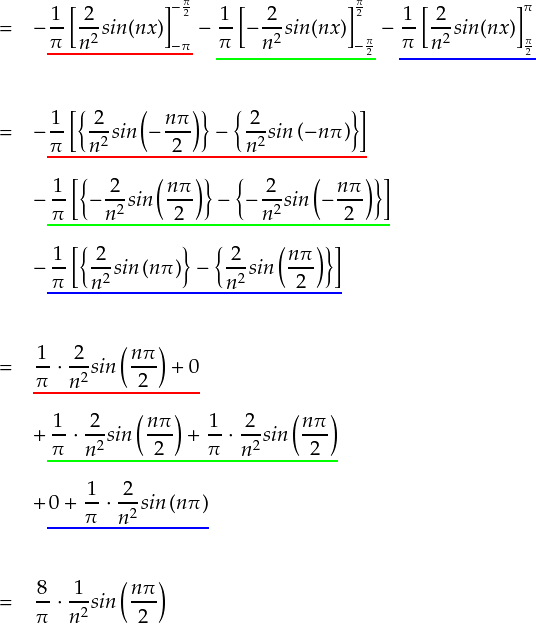
例によって,「sin(nπ) = 0 (nは整数)」,「sin(-x) = -sin(x)」の関係を使いました。 以上のことから,bnの値が求まりました。やれやれ。。。
ここまで求めたフーリエ係数を使って,三角波をフーリエ級数として表わすと次式のようになります。
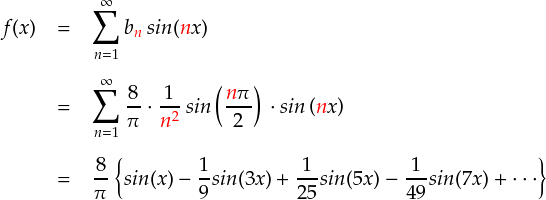
ちょっとN番目までの有限の級数について変化を見てみます。
| N=3 | N=5 | N=33 |
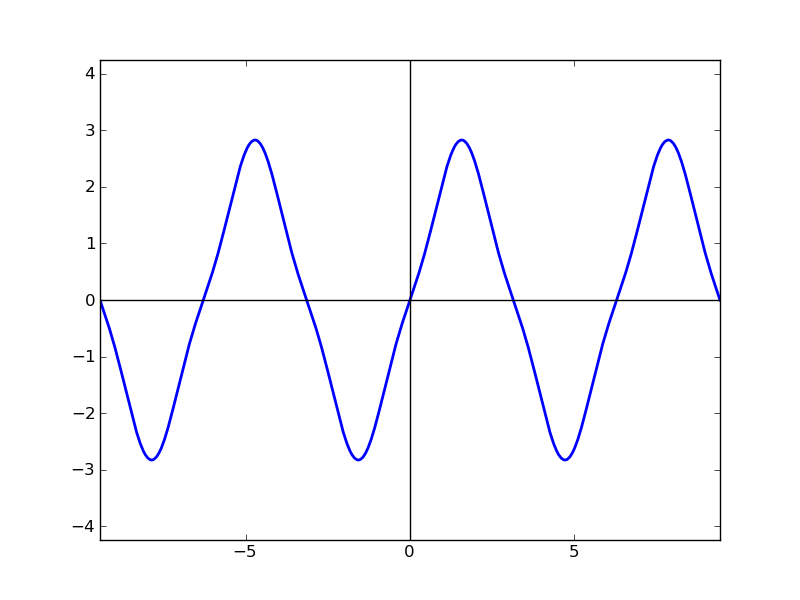
|
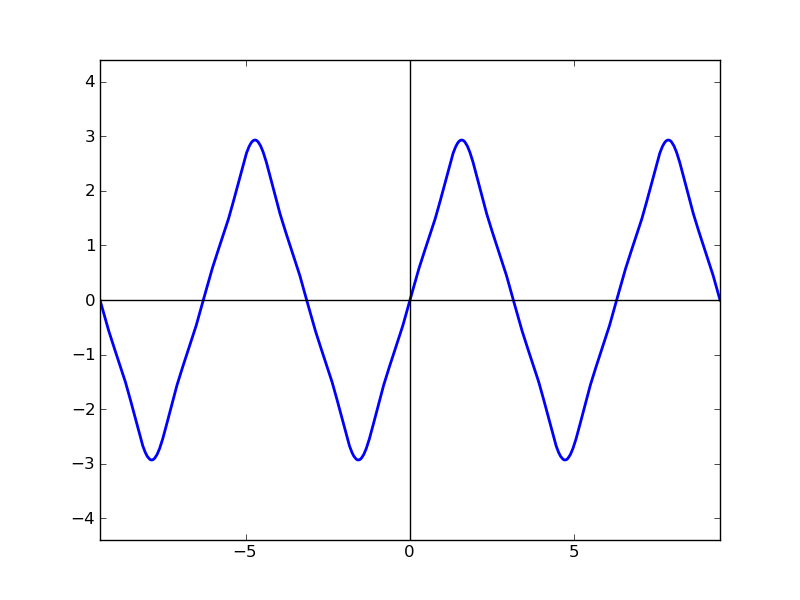
|
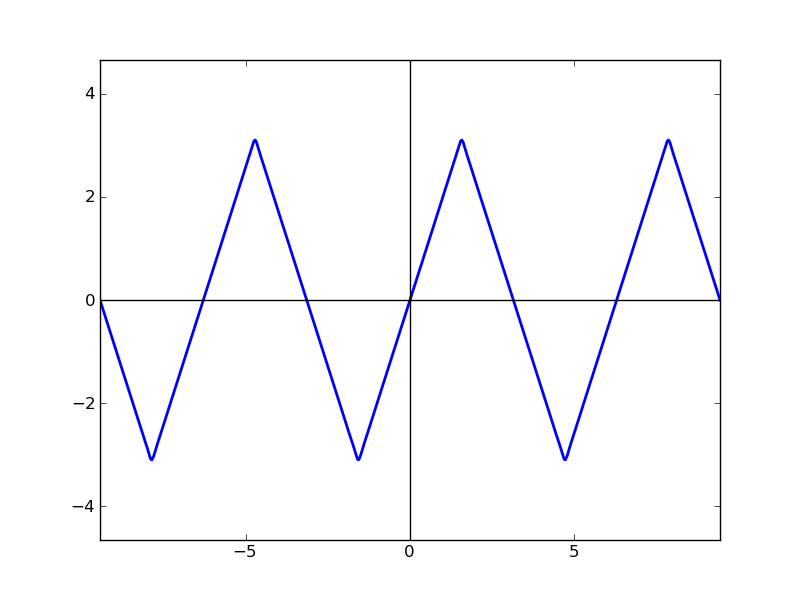
|
N=33でも,けっこうトゲトゲしてきます。
今回の計算はかなり面倒でした。もうやりたくないです。。。ということで,次ページでは計算量を減らす方法を考えます。