トップページ > フーリエ変換入門(FFT入門) > フーリエ級数(6)
前回の三角波のフーリエ係数を求める作業は,ちょっと面倒でした。 (あのくらいの手計算はスラスラできないとマズイのかもしれませんが・・・) それにしても,前ページでは頑張って計算した a0 や an がゼロという結果でした。 なんだか損した気分(?)になります。 フーリエ係数がゼロになるということは,その項はフーリエ級数になんの寄与もしません。最初から「いらない成分」なのだと分かっているならば,a0やanの計算を省いてしまいたいところです。
そんなわけで,最初に関数のグラフをパッと見ただけで,フーリエ級数展開するときに省ける計算をすぐに見分ける方法を考えていきます。
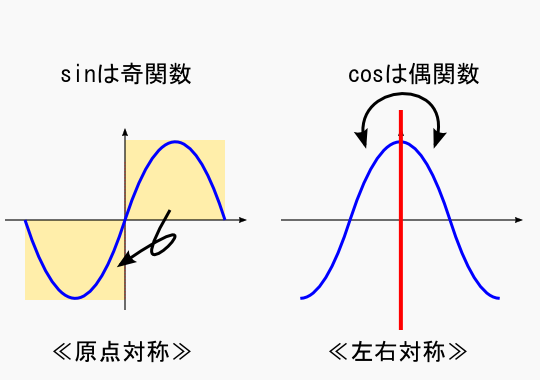
「偶関数」,「奇関数」という言葉がありました。おおざっぱに言えば,グラフの形の話だと思います。 グラフの形が,原点を基準に「点対称」になっている関数を奇関数と呼ぶそうです。数式で書けば「f(-x) = -f(x)」が成り立つのが奇関数です。
また,グラフの形がy軸に対して「線対称」になっている関数を偶関数と呼びます。数式で書けば, 「f(-x) = f(x)」が成り立つものが偶関数です。

そうすると,ちょうどsin関数は奇関数に,cos関数は偶関数になっていることが分かります。
さらに,sinとcosは直交しているので,互いには共通の成分を一切持ちません。 つまり,奇関数はsinだけで表現可能,偶関数ならcosだけで表現可能・・・ということになります。
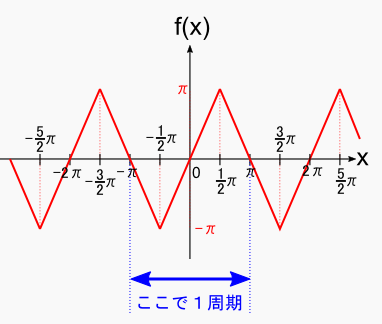
前ページでフーリエ級数展開した三角波をもう一度見てみます。この三角波は原点対称になっていました。 よって奇関数です。当然原点を通っているので,オフセット分のa0はゼロです。 また,偶関数としての成分も無いので,cos関数の係数であるanも全てゼロだった・・・と解釈できます。
そんなわけで,手計算でフーリエ級数展開を行う場合は,偶関数なのか,奇関数なのかを最初に確認しておくと, 計算量を大きく減らすことができます。
偶関数はcos関数だけで展開できるので,偶関数のフーリエ級数展開のことを「フーリエ・コサイン展開」とか呼ぶそうです。また,奇関数のフーリエ級数展開はsin関数のみで可能なので,「フーリエ・サイン展開」と呼びます。