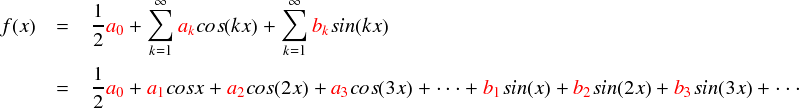
トップページ > フーリエ変換入門(FFT入門) > フーリエ級数(2)
フーリエ級数の中で,自由に設定できるのは a や b といった「係数」です。フーリエ級数の各項の係数は 「フーリエ係数」と呼ばれています。そのまんま・・・
フーリエ係数の添え字は,各項ごとに周波数が異なるcos関数(もしくはsin関数) の周波数と同じ数字を使っています。要は,フーリエ係数はそれぞれの関数ごとの「振幅」なので,各フーリエ係数を見れば「関数f(x)の中に,その周波数が成分としてどのくらい含まれているか」 が分かります。
実際にフーリエ級数を様々な関数に“似せる”ためには,フーリエ係数を調節することになります。 しかし,フーリエ級数の中には項が無限にあります。少なくとも“あてずっぽう”とかで全ての係数を決めていくのは不可能です。よって,目的とする関数からフーリエ級数を抽出する計算方法が欲しくなります。
またもや,おなじみ3次元ベクトルに戻って考えます。
3次元の場合は ex, ey, ez の3つの基底ベクトルがありました。これらの基底ベクトルどうしで内積をとると,互いに異なるベクトルどうしでは内積ゼロ(直交だから)となり,同じベクトルどうしの内積は1(長さが1だから)となるのでした。 ベクトルの内積のところでやった話と重複していますが, 今回の話題と強い結び付きがあるのでもう一度・・・。 何か適当な3次元ベクトルAに関して,各基底ベクトルとの内積を計算すると,
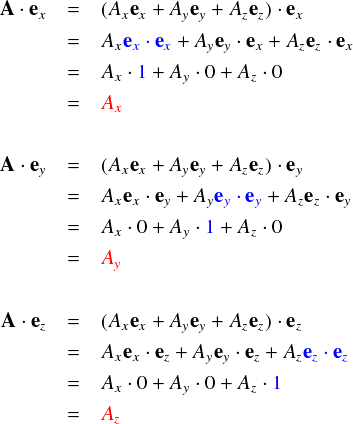
・・・という具合で,Ax,Ay,Azという各基底ごとの係数を取り出すことができるのでした。成分表示で書けば,もっと直観的です。
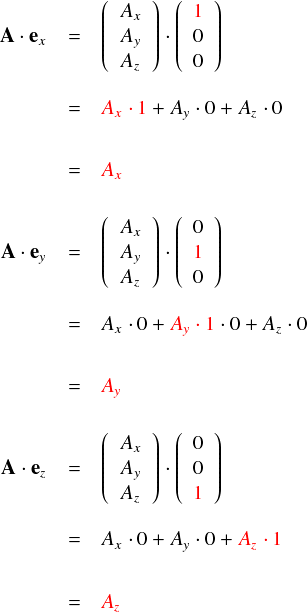
「基底ベクトル」は1つの成分のみが「1」で,他はゼロです。これと内積をとれば,欲しい基底の係数だけが取り出せる・・・という感じになってます。
今やりたいことは,「フーリエ係数を取り出す」ということでした。なんだか同じノリでやればできそうな気がします。
上で出てきた,おなじみの基底ベクトル ex, ey, ezは次のように書いています。
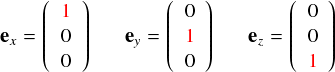
ではここで,「関数の基底」の候補としては定数,cos関数,sin関数があったことを思い出します。これらは直交していることを確認済みでした。3次元ベクトルの基底と同じ雰囲気を持っているわけです。よって,3次元ベクトルと同じノリで「関数の基底ベクトル」の成分を書きだすと次のような感じになります。 (「定数」の基底は 1 としてあります。何でも良いのですが,やっぱり1が分かりやすいので)
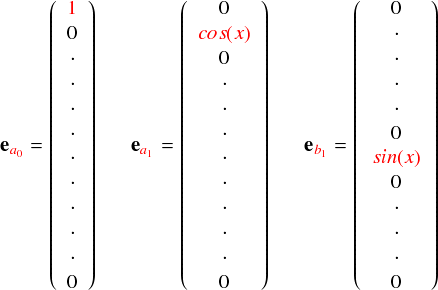
ただタテに並べてみただけです。。。ベクトルの名前は基底っぽく“e”としました。 添え字は,それぞれの基底に対応するフーリエ係数を使っています。添え字がa0の基底は定数項なので 1 ,添え字がa1だったら周波数1のcos,b1は周波数1のsin・・・という感じです。
ここまでで準備が整いました。3次元ベクトルと同じ方法を試してみます。すなわち,f(x)というフーリエ級数 (「フーリエ係数×基底関数の無限和」で表わされる関数) から,各基底の係数( = フーリエ係数)を取り出すために,「基底関数と内積をとる」ことをやってみます。
例として,cos(x)の項のフーリエ係数a1を取り出してみます。まずは普通に,関数どうしの内積をダラダラ書いてみます。
なお,前フリでやった通りcos(x)・cos(x)以外の内積はゼロなので,次式で出てくるほとんどの項はゼロになります。
cosx.png)
「cos関数の直交性」をたくさん使いました。そんなわけで,最後に残るのは a1 < cos(x), cos(x) > のみとなっています。
やはり,関数の内積は次式のようにベクトル風に書くと直観的だと思います。最初から直交性を意識して,cos(x)以外の基底要素をゼロにしてしまいます。次式でやっているのは,上と全く同じ計算です。
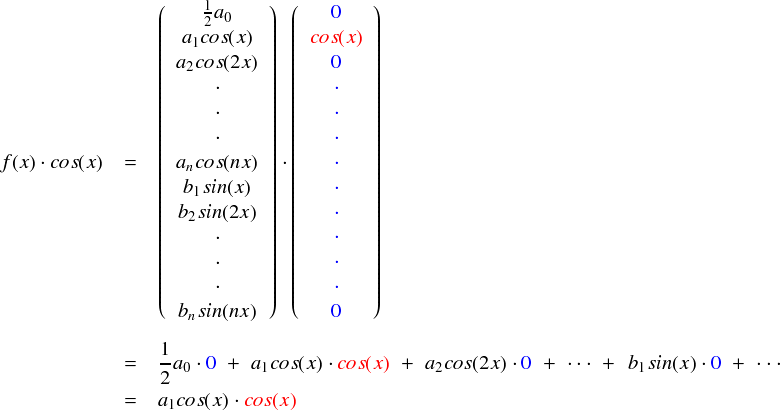
ここで,a1cos(x)・cos(x)というのは単なる積ではなくて「関数の内積」です。 関数の内積は,< a1cos(x), cos(x) > のようにも表記しました。そして,実際の計算は-π〜πで2つの関数の積を積分をするのでした (関数の基底,関数の内積で公式を作り,cos関数どうしの内積で計算方法を確認したやつです)。
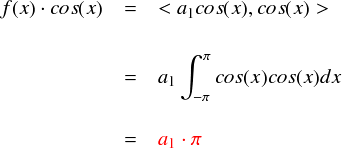
前に確認した通り,同じ周波数の三角関数どうしの内積は,「π」という値になります (ノルムの2乗ってやつです) 。 なので,今回のf(x)・cos(x)の結果は「a1π」となります。別にπはただの定数なので,割り算してしまえばスッキリします。
よって最終的に,フーリエ係数a1を取りだす計算は,
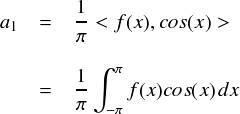
という感じになることが分かりました。結局,ある周波数成分のフーリエ係数を算出したい時は,「その関数と内積をとり,πで割り算すれば良い」ことが分かりました。しかし,3次元のベクトルの時は,「πで割る」なんてことは必要ありませんでした。 これは3次元ベクトルの基底は長さが1だったからです。三角関数はノルムの2乗がπとなってしまうため,このような操作が必要になっています。
次はa0,an,bnなど全てのフーリエ係数を揃てしまいます。