トップページ > フーリエ変換入門(FFT入門) > 前フリ(3)
【遊び方】
説明するほどたいそうな物では全くありません...
マウスを動かすと,そこにベクトルの終点が移ります。その動きに合わせてx軸上では赤いベクトル,y軸上では青いベクトルが動きます。それだけです。。。
いきなりベクトルの話です。しょっぱなから話が逸れてる感じですが,これが最終的に「sin関数とcos関数で全ての関数を表せる」という話につながったりします。 さらに,今後フーリエ解析について色々話を進める中で,難しそうな所ではイメージを固めるためにベクトルを考えます。フーリエ解析とベクトルはかなり強い結び付きがあったりします。
上のアプレットでは, 赤いベクトルはx方向という意味で ex , 青いベクトルはy方向という意味で ey と書いてます。 (以下,ベクトルはaのように太字で書きます。) これは普通のx軸とy軸をイメージしているので,言うまでもなく ex と ey は直角に交わっています。 あと, ex と ey の頭には ^ (ハット)がついていますが,これは「ベクトルの長さは1」という意味です。
ここで重要なのは, 平面上の全ての点を表現するには,長さ1で互いに直角なベクトルの ex と ey をそれぞれ適当に“伸び縮み”させて足し合わせればよいということです。 これを数式で書き表したものが,アプレット右下の表示となっています。
当たり前のことを何度も言いますが,2次元平面上ではどのような場所でも ex と ey を組み合わせれば指定できます。 さらに,ある点を指す場合に,その時の ex と ey の係数の組み合わせは「1通りだけ」に定まります。 2次元平面上の点なんて無限にあるのに,たった2個のベクトルだけで表せるなんて,当然のこととはいえ, ちょっとすごいです。。。z軸方向に ez を導入すれば,今度は3次元空間のすべての点を指定することができるようになります。
ex と ey のように,「そのベクトルを組み合わせれば,平面上の全ての点を指定できる」ものを 「基底ベクトル」 と呼ぶそうです。基底・・・いろんな物の「もと」という感じでしょうか。英語では“element”とか呼ぶのだと思います。 そんなわけで基底ベクトルは普通の教科書で「e」と書かれます。
もうちょっと2次元ベクトルの話を続けさせてください。。。 次はベクトルの内積の話です。
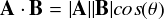
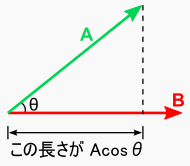
一応,内積の計算とはどんなものだったか書いておきます。 ベクトルAのうち,ベクトルB方向の「成分」が |A|cosθという「長さ」です。そこにベクトルBの長さ|B|をかけた値が A・Bなんです・・・。そんなことを言っているのが「内積」です。 正直なところ,使いどころがイマイチよく分かりません。
しかしここで,ベクトルBを「基底ベクトル」(たとえばex)にしてみると,「内積」の言いたいことがちょっと分かりやすくなります。
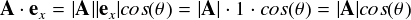
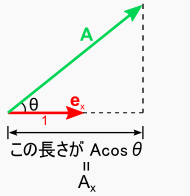
この場合,exの長さは「1」なので,内積を計算すると 単純に「ベクトルAのex方向の成分」が出てきます。 この数字を「Ax」と書くことにします。 同様に,ベクトルAとベクトルeyで内積をとれば, 「ベクトルAのey方向の成分」を取り出すことができます。 これを 「Ay」と書けば,
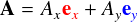
と,適当なベクトルAを exと eyで表す形式になりました。アプレットで表示している数式はこれです。 ここまで,それほど派手な計算はやっていませんが 「基底ベクトルと内積をとると,その方向の成分を取り出せる」 というのは非常に重要です。フーリエ変換をやる上で常に意識する事柄だったりします。
もしかしたら前ページの文脈から気付かれているかもしれませんが,この「基底ベクトル」と同じノリの「基底関数」みたいなものがある・・・かも? → それを使えば全ての関数を表せるかも? → 「基底関数」ってもしかして三角関数のこと? とか,そんな想像をするのは自然な流れだと思います。
結論を出す前に,あと少しだけベクトルの内積の話を続けます。。。
さっき使ったベクトルの内積というのは,|A|とか|B|とか,「長さ」という図形的なパラメータを使っていました。しかし,ベクトルには「成分」というものもあります。座標みたいなイメージのアレですね。
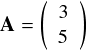
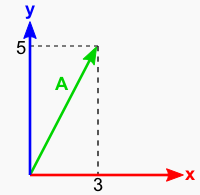
上のように書いた場合,ベクトルAのx成分は3, y成分は5・・・という意味でした。これは A=(3, 5) みたいに横に書いても同じ意味ですが,横書きだと後々面倒なことになるので縦書きに統一しておきます。 なんというか,この書き方は「基底」をすごく意識している気がします。全てのベクトルは ex と ey と表わせるので,それぞれの係数だけを書いてしまおう・・・という感じに見えます。
では,この成分形式の場合の内積はどうやって計算するかというと,
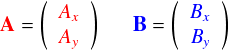
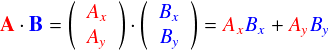
という感じで,x同士,y同士で成分をかけ合わせて,足し算するという形になります。 この内積計算のやり方はすごく重要です。今後ずっと使います。。。 では,さっきやったのと同様に,ベクトルAの相手が基底ベクトルex の場合を考えます。 ex を成分表示すると次のようになるのでした。
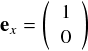
exは,単純にx成分に1を持ち,y成分はゼロ・・・という基底そのまんまな感じです。 これと内積を取ってやると,
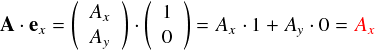
ということで,やっぱりAxがでてきます。 ex の x成分は1,y成分はゼロなので,ベクトルAの x だけが生き残る感じになっています。
ついでに, 3次元の基底 ex, ey, ez も書いておきます。 3次元になってもイメージは全く同じです。
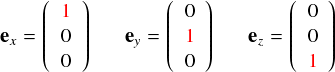
最後に,ベクトルAが3次元の場合の各成分の出し方を見てみます。 これも全く同じ感じで・・・
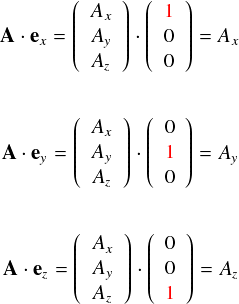
ベクトルAが2次元だろうと3次元だろうと,「基底ベクトルと内積をとれば,その成分が取り出せる」ことには変わりありません。極端な話,ベクトルの次元が「無限次元」だったとしても通用する気がします。イメージ的に。
そんなわけで,ここまで重要なベクトルの性質を確認しました。「基底ベクトル」とか,「成分を使う内積の計算」とかは後々まで使います。
とりあえず,次ページでは三角関数に話を戻します。 今回確認したベクトルの内積の拡張として,「関数どうしの内積」の話になります。