トップページ > フーリエ変換入門（FFT入門） > 収束定理（２）

証明の方針

「収束定理」から手を付けます

最初に，何から片付けていくかを整理します。

前ページでは「三角関数で全ての基底が揃ったのか」と，「フーリエ級数は様々な関数と一致できるのか」 という，2つの関心事が出てきました。 2つの事柄は別々のように見えますが，証明をやってみると途中までは両方とも似たような流れになります。 そんなわけで，最初は「フーリエ級数は様々な関数に一致（収束）する」という，いわゆる「収束定理」の証明からやっていきます。そのほうが式変形のモチベーションがはっきりしているので・・・

有限項のフーリエ級数

まずは，おなじみフーリエ級数を出しておきます。これをどんどんいじっていくことになります。。。

ここまで出てきた「フーリエ級数」は無限項までの和でした。 それとは別に，今回はこれを途中で止めてしまい，「第N項までの和」を考えておきます。 このN個の項の和を「S_N」と書くそうです。コンピュータ上で計算するときは無限なんて不可能なので， 結局この「フーリエ有限和」を扱っている感じです。　フーリエ級数は英語だと“Fourier Series”とか言うらしいので，その頭文字をとって“S”なんだと思います。それで，N番目までのフーリエ級数だから「 S_N(x)」です。そのまんまです。

そもそもフーリエ級数は，「ある関数f(x)に似せたもの」というイメージでした。 フーリエ有限和の場合は，項の数が限られているので「本物」のf(x)から多少ズレがあります。 前に出てきた三角波で，ちょっとイメージしてみます。

N の値をいろいろ変えてグラフを書いてみます。

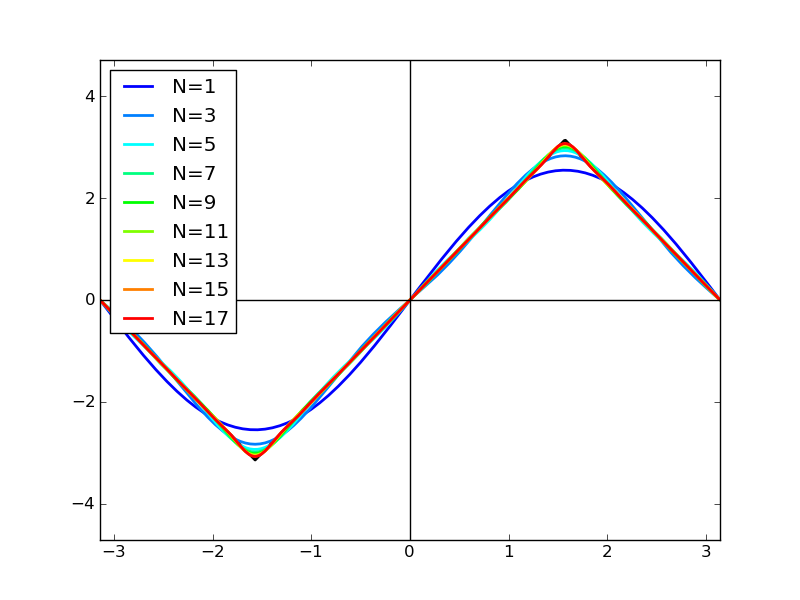
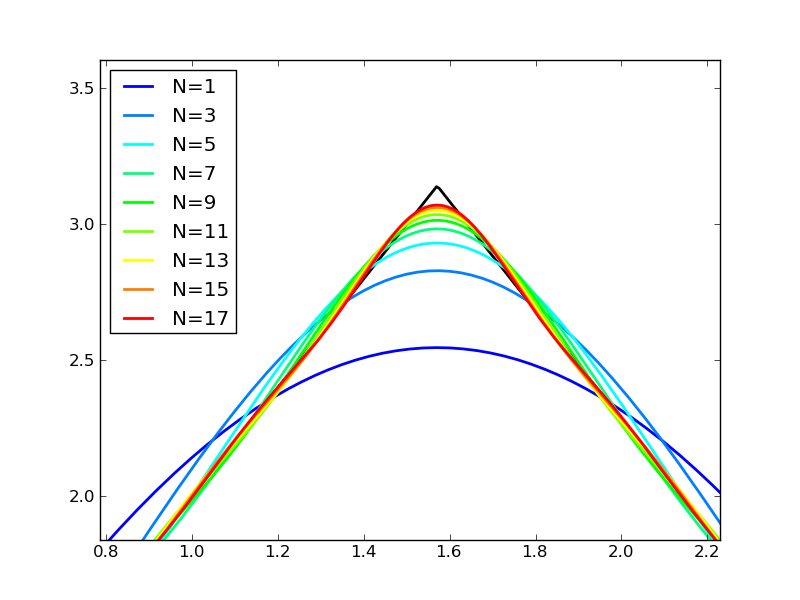
ちょっと見づらいので，トンガリの先端を拡大。 たしかに，N の値が大きいほど「本物の三角波」に近づいていることが確認できます。

上のグラフの様子だと，「フーリエ有限和」のS_N(x) は，だいたい本物のf(x)に近いということが確認できます。あえて数式で書けば次式のような感じです。

「だいたい近い」とは言っても，近似の程度はNの値によってだいぶ変わる気がします。 Nが小さいときはズレが大きく，Nを大きくするにつれて精度が良くなっていきます。 だったら，Nの値を無限大まで飛ばせば，「完全にf(x)に等しくなる」のでは・・・？　 という雰囲気になってきます。

これは「引き算すればゼロ」になる，と書きなおしたほうがすっきりします。 最終的にこれを証明することになります。

どんどん代入して考えやすく

これから証明したい式は，次式となっています。

これでは手のつけようがありません・・・。まずS_N(x)がブラックボックスなので， とりあえずフーリエ有限和のS_N(x)

を代入して，中身をちゃんと書いておきます。

・・・まだフーリエ有限和とf(x)の関係が見えません。 ここで，フーリエ係数 a₀，a_n，b_n は次式のように，f(x)を元にして計算しているのでした。

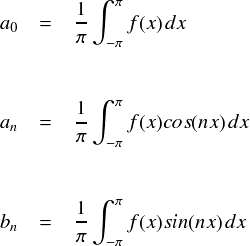
とりあえずこれも代入します。

何も考えずにa₀，a_n，b_nを代入してしまいましたが， これだと関数の変数である「x」と，各フーリエ係数の積分変数である「dx」 が，同じ「x」と書かれていて非常に見づらいです。積分変数の場合，定積分の計算に使う変数というだけなので， 外部から影響は受けません。なんというか，「積分計算の中で閉じている変数」という感じです。

そんなわけでフーリエ係数を計算するときの積分変数は「y」として，別の文字を使うようにしておきます。

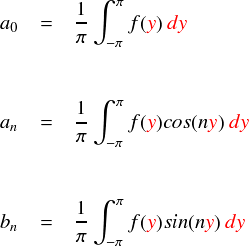
それでは改めて代入・・・

なんだかごっつい感じになってしまいました。。。 （画面からはみ出てしまったらごめんなさい・・・）

一見するとかえってゴチャゴチャしてしまった感じですが，上の式中では各項にf(x)が含まれているので，f(x)でくくってみたり，いろいろできそうです。 とりあえず手をつけやすい形まで持ってこれた，ということで。

次ページではもっとスッキリまとめるために，もう少しだけ変形していきます。

前へ　 次へ