トップページ > フーリエ変換入門(FFT入門) > 収束定理(1)
一番最初は,「三角関数を重ね合わせれば様々な関数を表現できるらしい」というところから始まりました。 その後,三角関数の直交性,フーリエ級数,フーリエ係数と進んできて,あの角ばっている矩形波をsin関数で表わす方法も分かりました。今のところ,確かにそれっぽい雰囲気になりつつあります。
しかし,「様々な関数」を表すのに,三角関数だけで十分だという保障はありません。例に挙げた矩形波は,「たまたまsin関数を使って表わせただけ」なのかもしれません。 これを確認する方法を考えたいところです。
さらに,たとえ三角関数と定数だけで事足りるとしても,フーリエ級数が様々な関数とぴったり「等しく」なるのか分かりません。 もしかしたら「近似」というだけかもしれません。実際にコンピュータ上で計算するときは無限の計算なんて不可能なので,実用上は「近似」で十分な場合も多いです。それでも,数学的に「イコール」と「近似値」は,だいぶ違います。これも確認できればスッキリできそうです。
そんなわけで,ここからの流れは以下の2点を確認する話になります。
前フリの内容で,「三角関数の直交性」は確認済みです。そのことから,「sin関数,cos関数,定数」は基底のように見えるという話もありました。さらに,それらの「基底関数」をフルに使った「フーリエ級数」を作って,矩形波を再現したりもしました。 しかし,本当に三角関数と定数で全ての基底となっているのでしょうか。。。
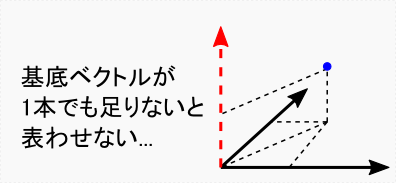
例のごとく,3次元ベクトルの場合をイメージします。

もし1本でも基底ベクトルが欠けてしまえば,当然の事ながら,空間内の点を全て表すことは不可能になってしまいます。これと同様に,もし「関数の基底」が足りていなければ,やはり「様々な関数を表現できる」と言いきることはできません。フーリエ級数が万能の雛型ではなくなってしまいます。 3次元ベクトルのイメージは簡単ですが,関数の基底の話になるともはやイメージで片付けることはできません。 イラストによる直観的イメージが難しい以上,これは数式で処理する他ないように思います。
たとえば,おなじみ(?)の背理法を使う証明なんかが考えられます。「三角関数以外にも,もう一本だけ直交する基底関数がある」と仮定して,いろいろ式変形をします。すると,最終的に出てきた式は最初の仮定に矛盾する・・・ とか。とりあえず今は,そんな感じになることを期待しておきます。
次ページ以降で詳しく扱います。
もうひとつの大きな問題は,本当にフーリエ級数が様々な関数と一致する可能性を持っているのか,ということです。 前フリで矩形波を作った時は,確かに周波数が奇数倍のsin関数を重ね合わせていけば,矩形波っぽくなっていく様子が確認できました。しかし,それが「様々な関数」になった場合,どこまで対応できるかはわかりません。
そうは言っても,関数の形(波形)なんて無限にあります。1つ1つ確かめるのは大変なので,一括して調べられる方法を考えます。たとえば,単純に適当な関数f(x)とフーリエ級数を引き算して,その結果がゼロになれば・・・ などと考えてみます。
これからの内容は,別にフーリエ解析処理を行う上で必須の知識なのか微妙です。 いくつかの重要な証明の結果だけを覚えておけば良いのかもしれません。。。 ただ,根っこの部分の理解があれば,いざという時に解決策に辿り着く可能性が増えます。 一応確認ということでやっていきます。