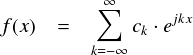
トップページ > フーリエ変換入門(FFT入門) > 複素フーリエ級数(2)
大学の研究室が忙しすぎて,半年以上非常に中途半端なところで止まってしまいました。。。ちょっとこれまでの文脈を忘れているので,話が飛ばないように丁寧に進めます。以前の内容と重複していたらごめんなさい。
たしか,前ページでは「複素フーリエ級数」を作ったのでした。非常にコンパクトな形にまとまっているのが魅力です。
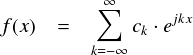
このフーリエ級数を使いこなすために,各項の係数ckを求める方法を調べます。 いまのところ知っているのは,下の3式のような関係だけです。 これまで使ってきたakやbkといった 三角関数表現のフーリエ係数と,今相手にしているck(複素表現形式のフーリエ係数)の関係です。
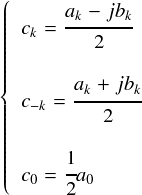
一応,上の式を使えば,既に知っている方法 (実数のフーリエ係数を求める方法です) でaとbを求めて,そこからcを導出・・・ということが可能です。 しかし,せっかくejkxを使ってフーリエ級数をコンパクトにしたのに,わざわざ面倒な三角関数表現に戻るのは損な気がします。 ここは,フーリエ係数もejkxを使って求められると嬉しいところです。
まず最初に,適当な周期関数f(x)をイメージしておきます。波動関数ejkxを使った,複素表現をすると以下のような感じになります。 今後は「フーリエ級数」と言えば常にこの複素形式のフーリエ級数を指すと思ってください。
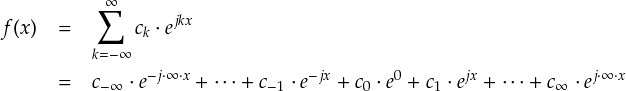
ここで,f(x)の各項の係数を取り出すことを考えます。 とりあえず, フーリエ係数(1) のところでやったのと同じ方法をとることにします。 すなわち,f(x)と,欲しい周波数kをもったejkxとで内積をとる計算をします。
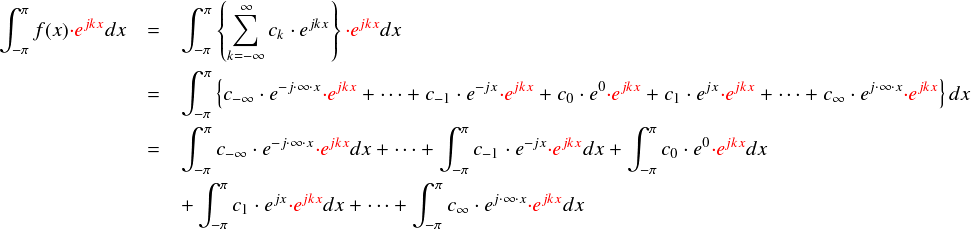
ゴチャゴチャしているように見えますが,単純にejkxを各項にかけて積分しただけです。各項は1周期π〜-πでの積分なので,普通に手計算することができます。 以前のフーリエ係数(1)と同じ結果を期待するので, 係数がck以外の項は消えることを期待しているわけです。
1つ1つの項をチェックするのは面倒なので,例のごとく適当な整数のmとnの場合で一気に片付けます。
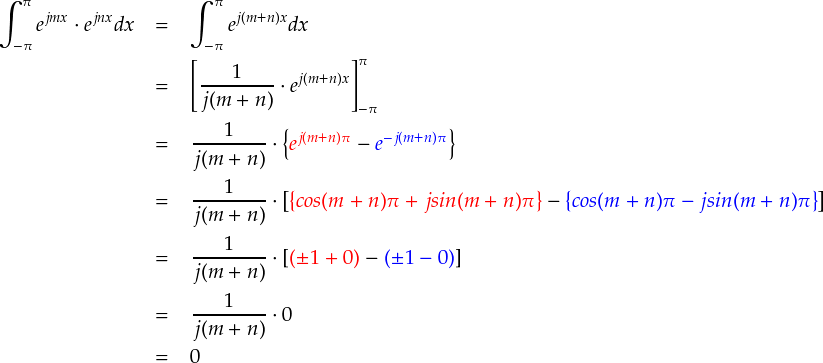
・・・というわけでmとnがどんな整数であっても,ejmxとejnxの内積はゼロになることがわかりました。 これは望んだ結果のように思えますが,ちょっとマズイです。取り出したかったejmxを係数に持つ項も消えてしまったからです。。。
くどいですが,ejkxどうしの内積をとってみます。
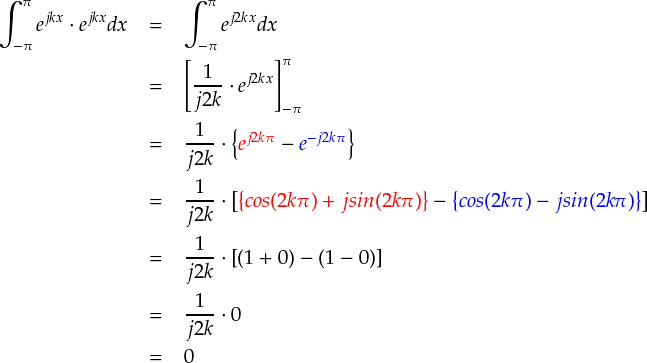
やっぱりゼロになってしまいます・・・。前にやったsinやcosでは,自分自身(同じ周波数どうし)との内積だけはゼロにならなかったので (三角関数の直交性の話です), それと同じノリでなんとかなると思ったのですが,アテがはずれてしまいました。
ここまで,ある周波数kの項であるck・ejkxの係数,ckを取り出そうとしてきましたが, なかなかうまくいきません。なんとか内積をとってゼロにならない方法が欲しいところです。
そもそも,ejkxという関数はどう頑張ったところで,1周期で積分すれば必ずゼロになってしまいます。 よって,積分してゼロにならないようにするためには,係数が欲しい項のejkx自体を消す必要があります。 全体にゼロをかけても意味がないので,それ以外でejkxを消す方法としては,次のようなものが考えられます。
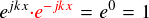
e-jkxをかけてk番目の項を“1”にしてしまうという手が使えることが分かります。 1にしてしまえば1周期で積分してもゼロになりません。これに対して,k番目以外の項は必ず波動関数が残るので積分すればゼロになります。 これでなんとか欲しい項だけを取り出すことができそうです。試しにf(x)とe-jkxとの内積をとってみます。
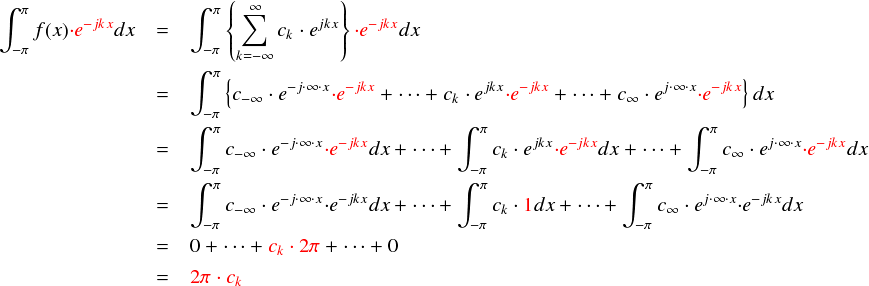
たしかに,欲しい周波数の項だけ残りました。ただし,1周期で積分する時に2πという余計な係数もついてきてしまいます。 これは単に割り算して解決してしまいます。以上から,周波数がkである項のフーリエ係数は,次の式で求めることができます。
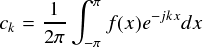
とりあえずckを求める方法は分かりました。基本的にこれはどんなkであっても通用します。 しかし,ckを求めた時に,ckの分母にkが入るような場合はc0を求める場合に極限計算が 面倒だったりします(次ページの矩形波のフーリエc0のような場合)。 c0は周波数がゼロの成分,すなわちもとのf(x)という波形を全体的に上下させるオフセット成分のような役割をします。 これを求める際は,ejkxと内積をとって後からk = 0を代入するのではなく, はじめからe0 = 1と内積をとる方法が手軽です。敢えて式で書けば,
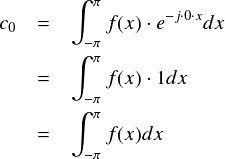
となります。単にf(x)を1周期(-π〜π)で積分するだけになっています。
ここまでで,「複素フーリエ級数」のあらわす意味,また,その関数の形を決めるパラメータである「複素フーリエ係数」の求め方が分かりました。 ところで,このFFT入門の冒頭の式(フーリエ変換の式) は下式のようになっています。
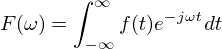
このフーリエ変換の式は,今回導出した複素フーリエ係数ckを求める式と非常によく似ています。というか,「フーリエ変換」というものの直観的イメージは 「複素フーリエ係数を求めている」と考えてもかまいません。本質的には同様のことをしています。
ここで一気にフーリエ変換まで行きたいところですが,ちょっとその前に確認をしておきます。 突然出てきた「複素フーリエ級数」,そしてその「複素フーリエ係数」を求める方法ですが,これは本当に従来のsinやcosを用いた実フーリエ級数と同じことを言っている のでしょうか・・・?いわゆる,両者の整合性はきちんとあるのか,ちょっと気になるところです。 次ページでは,実フーリエ級数であらわしていた矩形波と三角波を,複素フーリエ級数でも表すことを試します。