トップページ > フーリエ変換入門（FFT入門） > 複素フーリエ級数（１）

複素フーリエ級数

フーリエ級数をコンパクトにする

１つ前の節では，フーリエ解析から脱線して，e^jθ が「波動」を表しているという内容の「オイラーの公式」について確認しました。これからは，この e^jθ を使って フーリエ級数をよりコンパクトに表す方法を考えていきます。

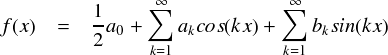
上式にはsinの項とcosの項が含まれていますが，それらを e^jθ だけを使って表わしてしまおう・・・ということをやります。まず，オイラーの公式は次のようなものでした。（プラス，マイナス両方書いておきいます。）

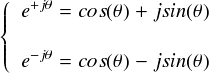
これを使うと，cos(θ)とsin(θ)は次のようにして作ることができます。

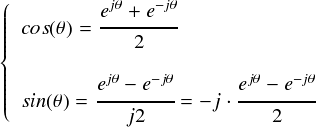
以上のsin, cos をもとのフーリエ級数の式に代入してみます。

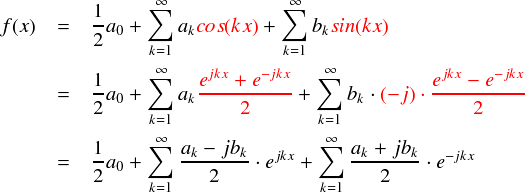
ここで，e^jθ と e^-jθ の係数は， jb_k　の符号だけが違います。虚部のプラス・マイナスが異なる複素数というのは「複素共役」と呼ぶのでした。なにか関係がありそうです。。

上式をもっときれいにまとめるために，a_k と b_k を次のようにまとめます。

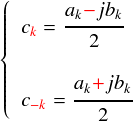
“c”というのが新しいフーリエ係数という感じです。いままで使っていた係数は a と b だったから順番的に“c”なのか，この係数が複素数(Complex number)だから頭文字をとって“c”なのか分かりませんが，とりあえずどの教科書でも c を使っているようなので慣例に従います。添え字はプラスとマイナスの両方を取ります。元々，フーリエ係数の添え字の意味は「k番目の周波数の係数」という感じでしたが，もはや数学的な処理を優先してるので意味は深く追わないことにしておきます。。

さてさて，上で定義した c_k を使ってフーリエ級数をきれいにまとめていきます。

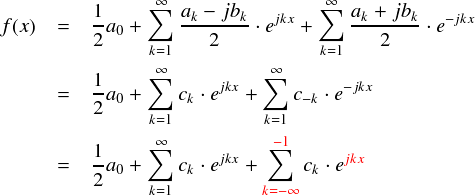
最後の行では，シグマの中を“c_k・e^jkθ”に統一するために k の扱いを工夫しています。 これで，上式の第２項と第３項では k が「-∞〜-１」と，「１〜∞」という範囲で値を取ることになっています。すると，kは整数だということを考えると，-∞〜∞のなかで唯一「 k = 0 」の条件のみ存在していないことに気づきます・・・。

さらに，今の流れは「 a とか b という係数を全部 c に置き換えてしまう」という感じですが，唯一 a₀ のみが残っています。 k=0 の時の c，すなわち　“c₀”を次のように定義すれば，フーリエ級数の式を非常にすっきりとまとめることができます。

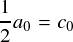
“c₀”というのは，e^0・jθ の係数ということになります。ここで， e^0・jθ = 1 なので，そのままシグマの中に組み込んで，次の式のようにまとめることができます。

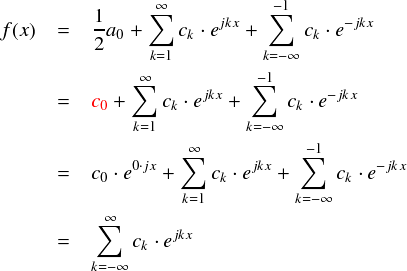
そんなわけで，フーリエ級数の式を非常に簡単に表すことができました。わざわざオイラーの公式を持ちだして，「波動」を e^jkθ と表わすことにしたモチベーションはここに由来しています。 一応，新しく出てきた係数“c_k”についてまとめておきます。

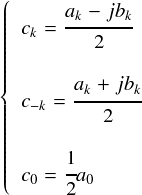
新しく定義した c_k という係数は，フーリエ係数（２）のところで導出した，a_k や b_k といった係数からできていました。復習ということで，もう一度出しておきます。

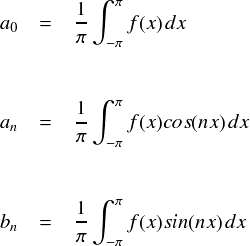
上式は，まだ e^jkθ を使わずに，sin や cos だけでフーリエ級数を作っていた頃に導出した公式でした。今や e^jkθ を使えば簡単だと分かっているのに，a_k や b_k を求めるために sin や cos に戻って計算をするのは面倒すぎます。。

次ページでは e^jkθ を使い，直接 c_k を求める方法を探すことにします。

戻る　 次へ