トップページ > フーリエ変換入門(FFT入門) > 複素フーリエ級数(3)

前に一度,矩形波のフーリエ級数展開でやった内容です。 今回は複素フーリエ級数であらわしてみます。 複素フーリエ係数を求めるには,次の式を使うのでした。
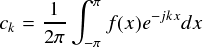
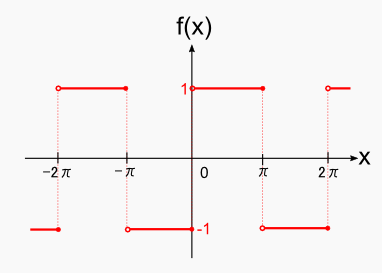
今回のf(x)は矩形波で,数式で表すと以下の通りになります。(実数でやった時と同じ関数を相手にします。)
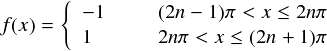
上の式は,いちおう「周期関数だ」ということを強調しています。 実際の計算では1周期だけを抜き出してejkxと内積をとるので, 相手にするのは以下の関数だと思って問題ありません。
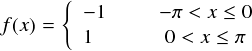
では,計算してみます。
深く考えずに,ただ計算します。 実数の時はak, bk ,a0と3種類計算する必要があったのですが, 今回はc0とckだけで済みます。計算量が少ないだけではなく,三角関数と比べて指数関数の積分は簡単なので楽に計算することができます。
まずはc0を計算します。
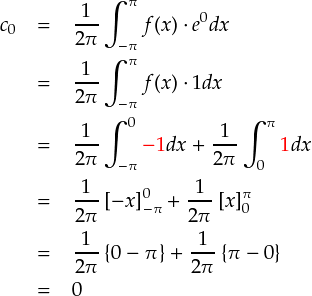
次に,ckを計算します。
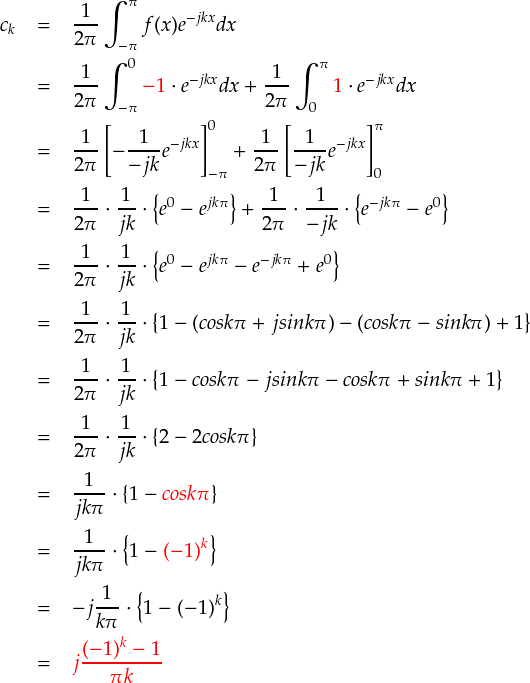
一応計算できました。しかし,これは実フーリエ級数展開した時の係数とはちょっと違う気がします。。。 参考までに,矩形波を実数のフーリエ級数で表した場合のフーリエ係数を再度書いておきます。 (ここで導出したものです。)
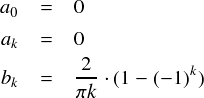
実数のフーリエ級数では,a0が定数項の係数,akがcos関数の係数,bkがsin関数の係数でした。 今回の複素フーリエ級数では,ejkx = coskx + jsinkx というsinとcosが合わさった波動関数に対して,ckという 「複素フーリエ係数」を定めています。なので,係数が完全に同じということは無いと分かります。
ここで,なんとなく共通点のようなものは見えています。 矩形波を実フーリエ級数展開した時は,ak = 0より,cosの項がなくなっていました。 今回の複素フーリエ級数展開ではckの値はjの付く項のみ,すなわち純虚数となっています。 すなわち,フーリエ係数の中で実数の項はゼロになっているということになります。 これは,ejkx = coskx + jsinkxに対して実部のcosが無いという意味です。 一応「矩形波はsinだけで表せる」という部分だけは共通しています。
先ほど求めたckを複素フーリエ級数に代入してみます。 実フーリエ係数と複素フーリエ係数がきちんと整合性を持っているなら,最終的には同じフーリエ級数が出てくるはずです。
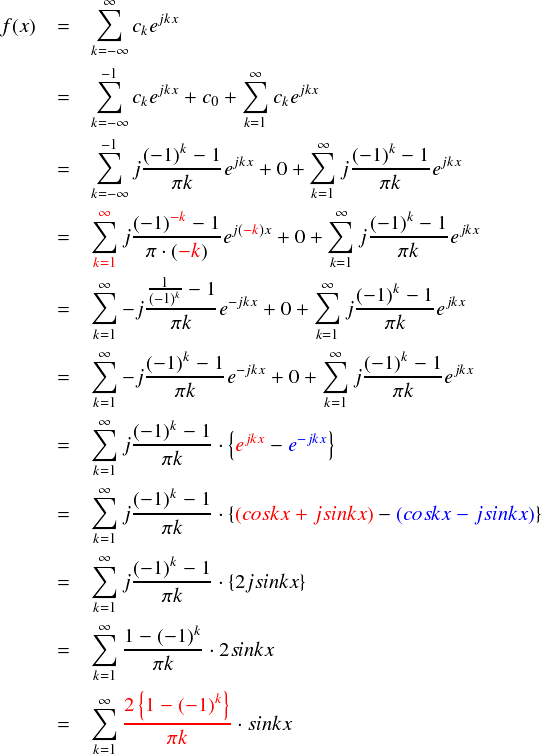
・・・ということで,確かに実フーリエ級数展開を行ったときと同じ数列であることが示されました。 たしか,実フーリエ級数展開をやった時は,ここから更にkが偶数・奇数のときの場合分けをやっていた気がしますが, 結局出てくるものは同じなので今回はここで式変形を止めました。
次は,三角波でも同じように複素フーリエ級数展開を試してみます。