�g�b�v�y�[�W > �g�����W�X�^���� > ���̉^���ʁi�Q�j
�u�}�N�X�E�F���������v�Ƃ������ƂŁC�d���C�w�̓��e����ʂ�m�F���܂��D
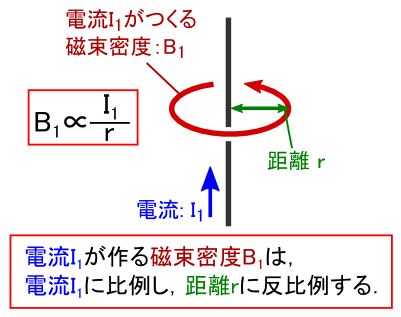
�O�y�[�W�ł́C���̉^���ʂ� �gp = E/c�h���ƕ�����C�ʎq�͊w�ł悭�o�Ă���gp = h/�Ɂh����Ƃ����b�ɂȂ�܂����D ���� p = E/c �Ƃ����W�́C�d���g�i���j�̕�������F�X�Ƃ�����Əo�Ă��܂��D ���̊W�������C�Ƃ����̂�����̃��`�x�[�V�����ɂȂ�܂��D
�Ƃ肠�����u�d���g�v�Ɋւ�鎮������Ȃ̂ŁC�܂��͓d���g�𐔎��ŕ\����Ƃ���n�߂�K�v�����肻���ł��D ���̂��߂ɂ́C�d���C�w�̊�b�������ł����u�}�N�X�E�F���������v�Ƃ�������g�����ƂɂȂ�܂��D �܂��͂�������ƃ}�N�X�E�F���������߂邱�Ƃɂ��܂��D�D�D
�i���d���C�w�͑�w�Ŕ��N�`�P�N�Ԃ��炢�̊��Ԃŋ������̂��Ǝv���܂��D �}�N�X�E�F���������Ƃ�����́C�d���C�w�̎��Ƃ̍Ō゠����Ɂu�܂Ƃ߁v�Ƃ��ďo�Ă����肵�܂��D �y�[�W���������ɂ��Ē��J�ɐ������悤�Ƃ��l�����̂ł����C �Ƃ肠�������̂P�y�[�W�����ň�C�ɂ��܂��D�K���ȁu���K�v�Ƃ������ƂŁD�j
������ƒ����Ȃ肻���Ȃ̂ŁC�C���f�b�N�X��t���Ă����܂��D
�Ƃ肠�����C�ȉ��̂S���͂܂Ƃ߂� �u�}�N�X�E�F���������v�iMaxwell's equations�j�ƌĂ����̂ł��D �}�N�X�E�F������Ƃ����l�iJames Clerk Maxwell�C1831�`1879�j�́C ����ȑO�ɔ�������Ă����d��⎥��ɂ��Ă̐�����F�X�Ƃ܂Ƃ߂������ł��D �d��⎥��̐����́C���̂S�̎��őS�ĕ\����炵���ł��D�������ł��ˁD
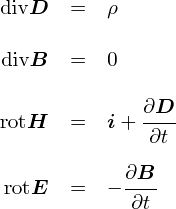
��̎��́u�����`�̃}�N�X�E�F���������v�ƌĂ����̂ł��D
�������gdiv�h�Ƃ��grot�h�Ƃ����L���́C �����̌v�Z�ɑ������܂��D ���̏��������ƌv�Z�̒��g��������Ȃ��̂ŁC ���̎��̂悤�ɁC�ށi�i�u���j�Ƃ�������g���ċL�q����邱�Ƃ�����܂��D
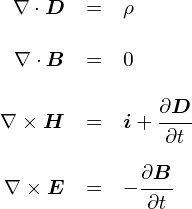
��̎��Ŏg���Ă���ށi�i�u���j�́C���̂悤�ȉ��Z�q�Ƃ������ƂɂȂ��Ă��܂��D
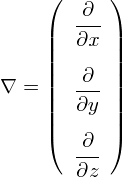
�����ł́C���̂��߂ɃR��������̂��悭������܂���D�D�D �Ƃ肠�����C���͌��邾���ŗ����܂��D
�����`�ɑ��āC�u�ϕ��`�̃}�N�X�E�F���������v�Ƃ����̂�����܂��D �����`�ł��ϕ��`�ł��C�����Ă��錻�ێ��͓̂������Ƃł��D ���Z�����ŏK���悤�ȓd���C�̘b�́C�������̐ϕ��`�̃C���[�W�ɋ߂������ł��D
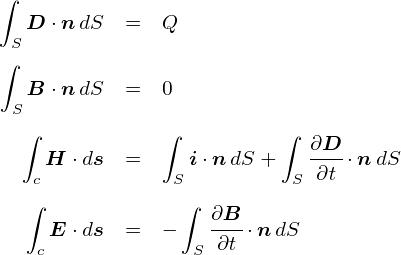
�����`�Ɛϕ��`����ׂď����Ă݂�ƁC�������������悤�ȕ��͋C�ɂȂ��Ă��܂��D

�ϕ��`�͂�����x�̑傫���������u�͈́v��ɂ��Ă���̂ɑ��āC �����`�͋�ԏ�̂����u��_�v�Ɋւ����̂ɂȂ��Ă��邻���ł����C ����͌�X�̐����ŁD�D�D �����`�͊���Ȃ��ƃs���Ƃ��Ȃ��\����������܂���D �������C�d���g�̕���������鎞�͔����`�̎�����������g���̂ŁC���߂Ɋ���Ă��܂������Ƃ���ł��D
��������́C�P�P�̎��Ɋւ��Čy�����e���m�F���Ă����܂��D ��ɍ��Z�����ŏK���b���ȒP�ɕ��K���Đϕ��`�̃C���[�W�����C ���ɔ����`�̎��ɃC���[�W�����т��Ă����E�E�E�Ƃ�������ł����܂��D �₽��Ɛ������o�Ă��܂����C�P�P�̘b�̓V���v���ł��D
�}�N�X�E�F���������̂P�߂́C�u�d��̐����v�ɂ��Ă̓��e�ł��D
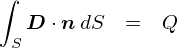
���ʁC�F�X�Ȑl�����������Ώۂ́u�����Ă���d�ׁv�C�܂�d���ł��D �~�܂��Ă���d�ׂɋ��������l�͂��܂肢�Ȃ��C�����܂��D �ł́C�Ȃ��d�ׂ������̂��H�ƍl����ƁC�u�d�ꂩ��͂��Ă��邩��v�Ɛ������邱�Ƃ������ł��D ����Ȃ킯�ŁC�u�d��v�ɂ��ďڂ����m�邱�Ƃ́C�d���C�w�̊�{���̊�{�������肵�܂��D
�u�d��v�̓g�����W�X�^�̓d���ɂ��čl�����ł��C�����Ēʂ�Ȃ����e�ł��D �u��v�̃C���[�W�ɂ��G��C������ƒ��J�ɐi�߂Ă����܂��D
�܂��́C���Ȃ��� �u�N�[�����̖@���v�iCoulomb's law�j ����n�߂܂��D
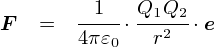
��̃N�[�����̖@���̎��́C���}�̂悤�ȃC���[�W�ł����D�iQ2���͂��ē������̓d�ׂ��Ƃ��܂��D�j
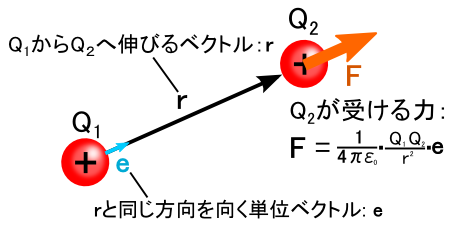
�u�d�ׂ���͂̑傫���v�́C �u�����̂Q��ɔ����i1/r2�j���āC�d�ד��m�̐ρiQ1Q2�j�ɔ�Ⴗ��v �Ƃ����@���ł��D �g1/4��0�h�̕����͎������킹�̌W���ł��D����ɂ��Ă͌�Ō@�艺���܂��D �͂���u�����v�̈Ӗ���t�������邽�߂ɁC�ge�h�Ƃ����P�ʃx�N�g�������Ă��銴���ɂȂ��Ă��܂��D
�P�ʃx�N�g�� e �� ���� r �̌����̒P�ʃx�N�g���Ȃ̂ŁC���̂悤�ɕ\������邱�Ƃ�����܂��D
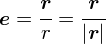
�ˑR �g e �h�ƌ����Ă�������Â炢�̂ŁC��̎��͐e�ȕ\���Ƃ��������ɂȂ�܂��D
���ɁC�u�d��v�iElectric Field�j�̃C���[�W�̘b�ł��D �d��̃C���[�W�́C�N�[�����̖@���Ƃ͎����Ă���̂ł����D �u������ Q1 ����͂���i���u��p�j�v�Ƃ��������ł͂Ȃ��C �u���̒n�_�ɂ�����d�� E ����͂���i�ߐڍ�p�j�v�ƍl����̂� �g�d��h�̃C���[�W�ɂȂ�܂��D �E�E�E�Ƃ͂����C Q1 �����d�� E �́C�����̂悤�Ɂu�N�[�����̖@������Q2�������������̎��v�ɂȂ�܂��D
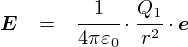
��̓d��̎��ł́C�uQ2�v�Ƃ������肪���Ȃ��Ȃ����̂ŁC �P�Ɂu�ʒu�x�N�g��r�Ŏw�肳���ꏊ�̓d��v��\�����Ƃ������ƂɂȂ�܂��D �������C�܂��܂��u���� r �v�������Ă��ĉ��u��p���ۂ������Ȃ̂ŁC��̎��͂��܂����������܂���D �u���̒n�_�ɂ�����g��h����͂��Ă���v�Ƃ������͋C������������Əo�������Ȃ�܂��D ���ǁC���ꂪ�g��h�Ƃ�����̃C���[�W�Ȃ̂ŁD
����Ȃ킯�ŁC����������u�d��̗l�q��\���g�d�C�͐��h�ɒ��ڂ��Ă݂悤�v�Ƃ�������ɂȂ�܂��D
�d�C�͐����u�����v�́C���̏ꏊ�Ńv���X�d�ׂ���u�͂̌����v��\���Ă��܂��D �܂��C�u�{���v�́C ���Ƃ����u�P�ʖʐς�����̖{���i�ʖ��x�j���d��̋�����\���v�Ƃ������܂�ɂȂ��Ă��܂��D ���Ȃ킿�C�d�� E ��ʂ̌������ŕ\��������u�d�C�͐����x�v�Ƃ������ƂɂȂ�܂��D �Ȃ��C�����Ō����u�P�ʖʐρv�́C�d�C�͐����ђʂ���ʂɂ�����P�ʖʐς��w���܂��D
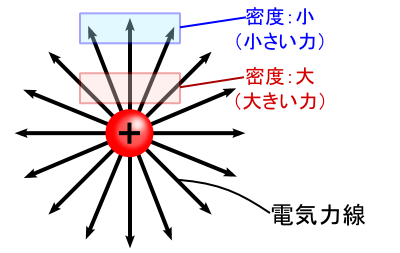
�d��̋����͓d�ׂɋ߂��قNj����Ȃ�C�Ƃ����̂͒����I�ɕ�����܂��i�N�[�����̖@�����j�D ��̐}�͓��ɉ����l�����C�d�ׂ���d�C�͐����S�����ɏo�Ă��銴���ŏ����Ă��܂����C �d�C�͐��̖��x�ɒ��ڂ���ƁC�m���ɓd�ׂ̋߂��ł͓d�C�͐��̖��x���傫���C�t�ɓd�ׂ��痣�ꂽ���ł͖��x���������Ȃ��Ă��܂��D �������ɁC �u�d�C�͐��̖��x�͓d��̑傫���ɑΉ����Ă���v�Ƃ������Ƃ������ł��܂��D
�u�d�� E �v�������錴���́u�d�� Q �v�ł��D �ł́C�ǂ�������猴���ł���u�d�ׁv�ƁC���ʂł���u�d��v�����ѕt������̂��l���Ă݂܂��D
���ǂ��ł����C�u�d�� E �v�Ƃ����̂́u�d�C�͐��̖��x�v�̎��Ȃ̂ł����D ���̂��Ƃ���C�u�����Ɠd�� Q ���傫���قǁC�d�C�͐��̖{���������Ȃ邾�낤�v �ƍl����̂͑f���ȗ��ꂾ�Ǝv���܂��D ����Ȃ킯�ŁC�Ƃ肠�����u�d�� Q ����o��d�C�͐��͉��{�Ȃ̂��H�v�Ƃ������Ƃ��l���Ă݂܂��D �����d�C�͐��̑��{�������܂�C�����K���ȖʐςŊ���Z���邱�ƂŁC ���̋�Ԃɂ�����u�d�C�͐��̖ʖ��x�v�����߂邱�Ƃ��ł��܂��D �܂�C�d�� E �̑傫����������̂ł��D
�u�d�C�͐��̑��{���v�����߂邽�߂ɁC���̐}�̂悤�ɁC �d�ׂ̊O�����{�[���̂悤�ȗe��ł�����ƈ͂ނ��Ƃ��C���[�W���܂��D ������C�u�Ȗʂň͂ށv�Ƃ�����ł��D�R�����̗��̂̃C���[�W�Ȃ̂ŁC�~�ł͂Ȃ����ł��D
�d�C�͐��̑��{���𐔂��������́C�u�Ȗʂ�˂�������{���𐔂���v�Ƃ����̂���Ԃł��D �d�ׂ�������ƈ͂�ł��܂��C���ɂ͂ǂ��ɂ������ꂪ����܂���D �������C�����Ō����Ă���u�˂�������v�Ƃ����\���ɂ́C������ƌ��܂莖������̂Œ��ӂ��K�v�ł��D
���̐}�́C�d�C�͐��̂P�{���Ȗʂ��ђʂ��镔�����g�債�����̂ł��D �g���h�ʂƌ����Ă��C �u���ɏ������������g�債�Č�������������ʂ��ۂ��Ȃ�v�ƍl����̂ł����D ����͔����̘b�ł����Ȃ��ݍl�����ł��D ���́u�����ȕ��ʁv�ɑ��ēd�C�͐������ʂ���ł͂Ȃ��C�i�i���ɓ����Ă����ꍇ���l���܂��D
���̏ꍇ�C�u�ʂ��т��d�C�͐��v�Ƃ��ăJ�E���g�ł���̂� �u�ʂɑ��Đ����Ȑ����̂݁v �Ƃ������܂�ɂȂ��Ă��܂��D �i�i�����ē����Ă�����̂ɑ��āC �u���ۂɌ����Ă��鐬���v�͐��ʂ�������Ă��鐬���̂݁E�E�E �Ƃ����l�����́C�f���Ȃ��̂��Ǝv���܂��D
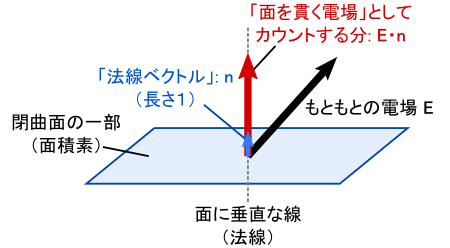
����𐔎��ŕ\���Ȃ��Ƙb���i�܂Ȃ��킯�ł����C�����ŏo�Ă���̂��u�@���x�N�g���g n �h�v�Ƃ�����ł��D �@���x�N�g�� n �́C���̖ʂɑ��Đ����ŁC�����P�̒P�ʃx�N�g���ł��D �����p�ӂ���C�gE�En�h�Ə������Ƃ� �u�d��̂����C�ʂɐ����Ȑ����v��\�����邱�Ƃ��ł��܂��D �x�N�g���̓��ς̒�`���̂܂�܂ł��D ���́u�@���x�N�g���gn�h�v�Ƃ�����́C�d���C�w�ł₽��Əo�Ă��܂��D �x�N�g�����ʂ��ђʂ���Ƃ����V�`���G�[�V�������p�o���邩�炾�Ǝv���܂��D�D�D
�ł́C�d�C�͐��̑��{���𐔂��܂��D �u�Ȗʁv�͂ǂ�Ȍ`�ł������̂ł����C�����ł͊ȒP�̂��߂Ɂu���v�œd�ׂ��݂͂܂��D �d������v���X�d�ׂ́C�s���悭�i�H�j���̒��S�ɒu���Ă��܂��܂��D
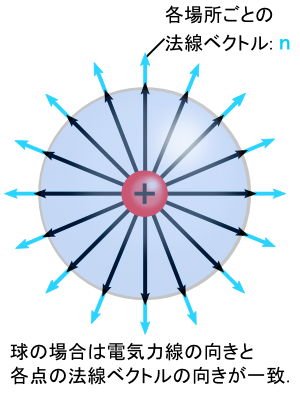
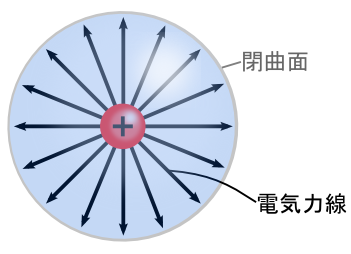
���̏ꍇ�C�d�ׂ���o��d�C�͐��͋��̕\�ʏ�̂ǂ��ł��u�ʂɑ��Đ����Ɋђʂ���v���ƂɂȂ�܂��D �i�~�Ƃ����̔��a�͉~����̐ڐ��ƕK�������ɂȂ��Ă���̂ŁD�j
�����ŁC���������Ǔd��̎����v���o���܂��D
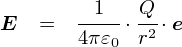
�ȖʂƂ��āu���v��I�ꍇ�C��̎��ł����ge�h�ƁC�@���x�N�g���gn�h�̌����͓����ɂȂ�܂��D �傫���͗����Ƃ��P�i�P�ʃx�N�g���j�Ȃ̂ŁC���ǁge�h�Ɓgn�h�͓����x�N�g�����Ƃ������ƂɂȂ�܂��D ���ʂ͂�����Y��ɂ͍s���Ȃ��̂ł����C����͋��ň͂�ł���̂ŐF�X�s�����悭�Ȃ�܂��D�D�D
��́C�u�d��E�́i�P�ʖʐς�����́j�d�C�͐����x��\���v�̂ŁC �d��̑傫���ɕȖʂ̕\�ʐς������Z�i���ρj���Ă��Γd�C�͐��̑��{�������܂�܂��D �܂��C�v�Z�ł� �u���̕\�ʐς� 4��r2 �v�Ƃ�������g���܂��D
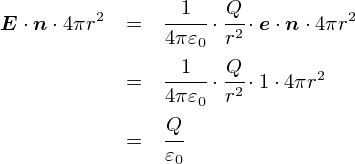
�E�E�E�Ƃ������ƂŁC�d��ɂ��ċL�q���Ă��鎮����u���� r �v�����Ȃ��Ȃ�܂����D ���̎��������Ă�����e�́C �uQ�N�[�����̓d�ׂ���o��d�C�͐��̑��{���́gQ/��0�{�h���v�Ƃ��������ɂȂ��Ă��܂��D ����ŁC�u�d��Ɋւ���K�E�X�̖@���i�ϕ��`�j�v�̏d�v�ȕ����͂��������I���ł��D ��������͂�����ƍׂ����b���l�߂Ă����܂��D
���ǁC�u�d�C�͐��̑��{���v�̎��͈ȉ��̂悤�ɂȂ����̂ł����C �₽����Y�킷���Ă�����ƕs�C���ł��D
�ǂ����Ă���Ȏ��ɂȂ����̂��C�l���Ă݂܂��D
���������C�N�[�����̖@���ɏo�Ă���gk = 1/4��0�h�Ƃ����W���́C ���̓d�C�͐��̑��{���̎����Y��ɂȂ�悤�Ɍ�t���i�H�j�ōl����ꂽ���̂Ȃ̂ŁC���R�Ƃ����Γ��R�ł��D ���̌W���́u�d�חʁi�P�ʂ̓N�[�����j�v�Ɓu�d�ׂɓ����́i�P�ʂ̓j���[�g���j�v�����ѕt����W���Ȃ̂ł����D ����͎��ۂɗ͂𑪒肵�Ď����ɂ���Č��߂邱�ƂɂȂ�܂��D�i�ʂ̕��@���������肵�܂��C��q�D�j �܂��C���Ƃ��Ɓu�P�N�[�����v�Ƃ����d�C�ʂ́C�ʂ́u�d�����m�ɓ����͂̎����v����ɂ��Č��߂��Ă��܂��D

�ł́C�ǂ����ČW��k�̒��g�� �gk = 1/4��0�g�ȂǂƁC �킴�킴�\���������̂ł��傤���D �܂��P�ڂ̗��R�́C���ǂ��ł����C�u�d�C�͐��̑��{���̎����Y��ɂȂ�Ɗ���������v�ł��D �����ɁC�W����P���Ɂgk�h�Ƃ����ꍇ�̓d�C�͐��̑��{���̎������Ă݂܂��D
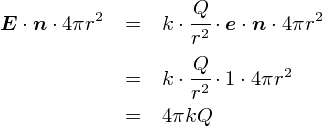
�ȂS�`�����Ƃ��������ɂȂ�܂����D�����ŒP���Ɏv���̂́C�u���萔k���g���~1/4�h�̌`�ŕ\���Ώ�̎��͖ł��ď����Y��ɂȂ邾�낤�v�Ƃ������ł��D �g4�h�Ƃ����̂͂����̐��i�������ʁj�Ȃ̂ŁC�g���h�̕����Ɏ�����w���킹��Ă��܂����Ƃ����l���ł��D ���������gk�h�̒l�͎����l�Ȃ̂ŁC�g���h�̕����́gk�h��1/4�Δ{�����K���Ȓ萔�Ƃ��āi����Ɂj���߂Ă��܂��܂��D
�����Y��ɖł��鎖���������߂ČW��k������������Ȃ�C�gk = A�~1/4�h�̂悤�Ȍ`�Ƃ��āC �V�����萔�gA�h��K���ɓ������Ă��̂��f�����Ɗ����܂��D �������C���ۂ͂����Ȃ��Ă��Ȃ��āC�gk = 1/A�~1/4�h�Ƃ����`�ŁC����ɒ萔�����Ă��܂� �i���ꂪ�g��0�h�ł��j�D �킴�킴�gk = 1/A�~1/4�h�̂悤�Ȍ`�ɂ���Ӑ}���C�ɂȂ�Ƃ���ł��D�D�D �����ɁC�����̌`�Ŏ������������Ă݂܂��D
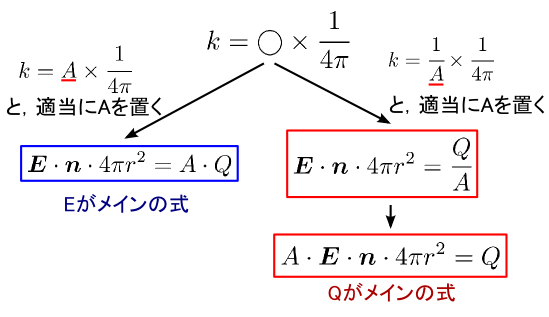
��̐}�ŁC�gk = A�~1/4�h�Ƃ����ꍇ�i�����j�ł́C�d�C�͐��̑��{���̎��� �u�d��E�ɋ��̕\�ʐς������Z���ēd�C�͐��̖{�������߂�ƁC�d��̌��̓d��Q��A�{�ɂȂ�v�Ƃ��������ɂȂ�܂��D �d��E�����̂܂ܖʐϕ������C���[�W�ł��D ����ɑ��āC�gk = 1/A�~1/4�h�Ƃ����ꍇ�i�E���j�ł́C���̕��͋C�� �u�d��Q���o���d�C�͐��̐��́C���������d��E�ɋ��̕\�ʐς������Z�����l��A�{�ɂȂ�v�ƂȂ�܂��D �������͓d��Q�̕��������炸�ɁC�d��E�̍��̕��Ɏ��������`�ɂȂ�܂��D
���ǁC�d��E����̂Ƃ��邩�C�d��Q����̂Ƃ��邩�̈Ⴂ������܂��D ���R�ł����C�u�֗��ȕ���I�т����v�Ǝv���Ƃ���ł��D
�����������l���Ă���̂́u�d�C�͐��̑��{���̌����v�݂����Ȃ�Ȃ̂ŁC �g�����h�Ƃ�������ɂ͗l�X�ȃV�`���G�[�V�����ɑΉ��ł���悤�ɂ������Ƃ���ł��D ���R�ł����C�g�d��Q�h�͂ǂ��ɂ����Ă��g�d��Q�h�̂܂܂ł��D��������������܂���D �������C�d��E�͎���̏ɂ���ĕω����Ă��܂��܂��D
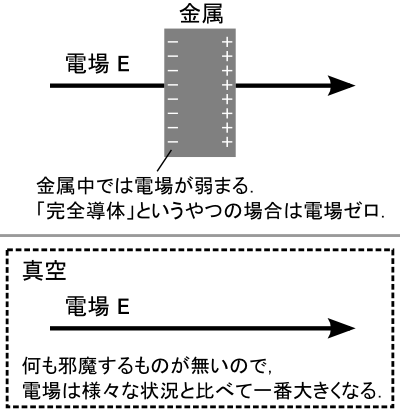
���ɒ[�ȏ�������ƁC �����i���S���́j���ł͓d�ꂪ�[���ɂȂ�܂��D �t�ɁC�^��̏ꍇ�͉��������������Ƃ������ƂŁC�d��Q�����d��͈�Ԍ����悭�i�H�j���݂ł��܂��D �ǂ���̃P�[�X�ł��C�g�d��Q�h�͓����傫���ł��D ����Ȃ�C�g��h�Ƃ���͓̂d��Q�̕����ǂ��̂ł́E�E�E�H�Ƃ����C���ɂȂ�܂��D ����Ȃ킯�ŁC�u�d�C�͐��̑��{���̎��v���g�d��Q�h�ɂ����Y��ɐ����ł���悤�ɌW��k�������邱�ƂɂȂ�܂����D ���̌��ʂ��C�gk = 1/4��0�h�Ƃ����`�ł��D Q�ɂ��Đ�������ƁC���ׂĕ����͏������Y��Ȍ`�ɂȂ�܂��D
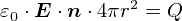
�����܂ł̘b���܂Ƃ߂܂��D�Ȃ��gk = 1/4��0�h�Ƃ���̂��C�����
�E�E�E�Ƃ��������ł��D
�Ƃ肠�����C�u�d��Ɋւ���K�E�X�̖@���i�ϕ��`�j�v�����������闬��ɍs���܂��D
�����܂ł̘b�ŁC�܂��́u�d��Q�����Q/��0�{�̓d�C�͐����o�Ă���v���Ƃ�������܂����D
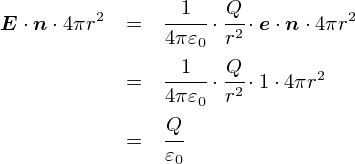
����ɁC������u�d��Q������v�Ƃ��������ɏ��������Ǝ��̎��ɂȂ�܂��D �i������0���ڍ����邾���ł����C������ƋC�����ς��܂��D�j
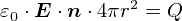
���ǂ��ł����C��̎��̍��ӂɂ́u�d�ׂ��͂ޕȁg�ʁh�ɂԂ���d�C�͐���S�đ������킹��v�Ƃ����C���[�W��̑��삪�܂܂�Ă��܂��iE�E4��r2�̕����j�D ���̑���͕��ʁC�u�ʐϕ��v�Ƃ������O�ŌĂ�܂��D �����ŕ\���ƁC���̂悤�ɂȂ�܂��D
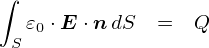
���ꂪ�u�d��Ɋւ���K�E�X�̖@���v�iGauss's flux theorem�j�̐ϕ��`�Ƃ�����ł��D ���̖��̂́C���̌�����������K�E�X����iCarl Friedrich Gauss, 1777�`1855�j�Ƃ����l�ɂ��Ȃ�Ŗ��t����ꂽ���̂ł��D �ϕ��ϐ���dS�̕���������ƁgS�h�ł��邱�Ƃ�������܂����C����͖ʐ�S��S�iSurface�j�ł��D �v�́C�K���ȕȖʂ̑S�ʐςɓn���āC�i�C���[�W��j�����ʐς��Ƃɕ������āC�d��Ɩ@���x�N�g��n�Ƃ̓��ς����S�������Z���Ă��������Ƃ����Ӗ��ł��D �i���̏ꍇ�͒P���ɕ\�ʐ�4��r2�������Z���邾���������̂œ��ɐϕ����Z���ۂ����Ƃ͂��܂���ł������D�j
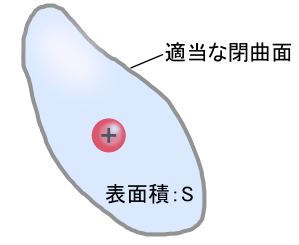
���ۂ̂Ƃ���C�d�ׂ��͂ޕȖʂ́i���Ă���j�ǂ�ȗ��̂ł��\���܂���D �~���ł��C�����̂ł�OK�ł��D ����̘b�ł͌v�Z���P���ŕ�����₷���u���v�ł��܂������C ��̐}�̂悤�ɓK���ȕȖʂ̏ꍇ�ł��C���{���̎����ʗp���邱�Ƃ𐔊w�I�ɏؖ����邱�Ƃ��ł��܂��D ���̏ꍇ���u���̊p�v�Ƃ��������������ōl����킯�ł����C�����ł͏ȗ����܂��D
���炽�߂āC�K�E�X�̖@���i�ϕ��`�j�̎������Ă݂܂��D
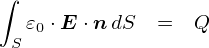
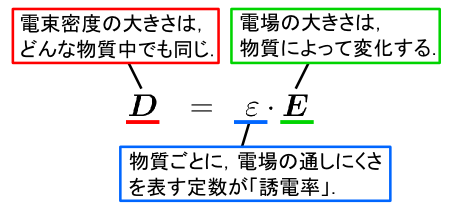
��̎��́C�u�d��E�͓d�C�͐��̖��x���v�Ƃ����C���[�W�Ɋ�Â��č�����̂ł����D �������C���ۂɖʐϕ�����Ă���̂��g��0E�h�ł����āC�g�d��E�h�ł͂���܂���D ���́g��0E�h�Ƃ��������܂�́C�u�d�����x�v�iElectric Flux Density�j�ƌĂ�Ă��܂��D �d�����x���g D �h�Ƃ����L���ŏ�����܂��D
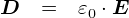
�d��E�́u�d�C�͐����x�v���������Ƃ��v���o���ƁC �d�����x�Ƃ������O���u�d���v�iElectric Flux�j�Ƃ������i�̑��j�����肻���ȕ��͋C���o���Ă��܂��D ���ہC�d�����xD�͓d��E�ɒ萔�������������Ȃ̂ŁC�d���̌`�Ƃ������C�����͓d�C�͐��Ɠ��������ɂȂ��Ă��܂��D �������C�傫���i�{���j�͈Ⴂ�܂����C�������Ⴂ�܂��D�D�D
�����d�����x D���g���ăK�E�X�̖@����\���ƁC���̂悤�ɂȂ�܂��D
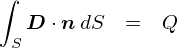
�����ς肵�����ɂ܂Ƃ܂�܂����D ���ꂪ�}�N�X�E�F���������̑�P���Ƃ������ɂȂ��Ă��܂��D
���̎��͂��Ƃ��Ɓu�d�C�͐��̑��{���v�����߂邽�߂ɍ���Ă������̂ł����D �������C��̎��Ŗʐϕ�����Ă���͓̂d�����xD�ł��D ����ƁC�������u�d���v�Ƃ��������d�ׂ���o�Ă��鎖���C���[�W����ƁC ���̎����u�d���̑��{���v��\�����Ƃ������ɂȂ�C ���̖{���́gQ�{�h���ƌ����Ă���킯�ł��D Q�N�[��������Q�{�̓d�����o�Ă���̂ŁC�P�N�[������������d�ׂ���P�{�̓d�����o�܂��D �d�����x�̎����́C��̎��œd�����x�ɖʐρim2�j��������i�ʐϕ��j����ƃN�[�����iC�j�ɂȂ��Ă��邱�Ƃ���C [C/m2]�ƂȂ�܂��D

�ł́C�ˑR�o�Ă������̓d�����x�Ƃ�����͉��H�Ƃ����b���Ō�ɏ��X�D�D�D
�d�����x�̘b�́C�≏�́i�U�d�́j�̒��̓d��̘b�����鎞�ɏo�Ă��܂��D �u���Ɂv�Ƃ�����ƊW������̂ł����C���̂Ƃ���ʂɐ≏�̂ɋ����͖����̂Ōy�������܂��D �i��X�CMOS�g�����W�X�^�̃Q�[�g�≏���̘b�ŏo�Ă���E�E�E��������܂���D�j �Ƃ肠�����C���ʂ̈�ʉ������b�ł́C�d�����xD�͕������Ƃ́g�U�d���Áh���g���Ď��̂悤�ɒ�`����܂��D
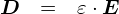
�����܂ł͈�ԒP���ȁg�^�h�̓d����l���Ă��܂������C �u�����d��Q�����d��ł����Ă��ǂ�ȕ����̒��ɂ��邩�œd��E�̑傫���͕ς���Ă��܂��v�Ƃ����b������܂����D �u�U�d���v�Ƃ�����́C����Ȏ��́u�d��̕ω���v��\�����肵�܂��D
�������ƂɗU�d���̒l�͌��܂��Ă���̂ł����C���̕������d���ʂ��ɂ����قǗU�d���͑傫���Ȃ�܂��D ����ƁC�d��̑傫���ƗU�d���̑傫���͑��E���邱�ƂɂȂ�̂ŁC�g�U�d���~�d��h�̐ς͌��Lj��̒l�ƂȂ�܂��D���ꂪ�d�����x�ł��D �ʂɓd�����x���͓̂d�ׂ���͂̑傫���Ƃ͊W����܂���D �������C�u�d��Q�����Ȃ�d�����x�����ŁC�d��̂悤�ɑ傫�����ς��Ȃ��v �Ƃ��������C�g�����h������Ŋ������̂ł��D�����Y��ɂȂ�̂ŁD�D�D
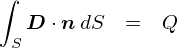
���ǁC�}�N�X�E�F���������̑�P���́u�d��Q�����d�C�͐��̑��{���v��\�����ł��D �d��E�́u�d�ׂ���́v�Ƃ��u�d�C�͐����x�v�Ƃ��C�C���[�W���₷���ʂȂ̂ł����C �}���ɂ���Ēl���ω����Ă��܂��̂Łg�����h�Ƃ��Ă܂Ƃ߂�ɂ͕s�s���ł��D ����ɑ��āC�d�����xD�͂ǂ�Ȕ}�������낤�Ɠd��Q�̑傫���ƈ�Έ�őΉ����Ă���̂ŁC ��̂悤�Ɂu�d��Q���o���d���̖{����Q�{�v�Ƃ����C�P�������Ȏ��Ƃ��Ă܂Ƃ߂邱�Ƃ��ł����E�E�E�Ƃ��������ł��D
�}�N�X�E�F���������̂P�߁C�K�E�X�̖@���́u�����`�v�ł��D
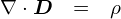
�����܂ł̓K�E�X�̖@���̐ϕ��`������Ă��܂����D �ϕ��`�́u�Ȗʂň͂ށv�Ƃ����͈̂ӊO�Ɓi�H�j���p�I�ŁC �R���f���T�Ȃ璼���́C�����P�[�u���Ȃ�~���Ƃ��������ŁC�u��Ԃ̕Ȗʁv�݂����Ȃ�����܂��Ă��܂��D �������C���́u�ϕ��`�v�Ƃ�����́C�u������x�L�������͈͂̓d����܂Ƃ߂Ĉ����v �Ƃ����ꍇ�����g���܂���D
�u�����`�v����郂�`�x�[�V�����́C�L�������͈͂̓d��ł͂Ȃ��C�u��ԏ�̂����_�v�̓d����s���|�C���g�ň��������E�E�E �Ƃ��������ł��D
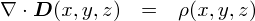
�u��ԏ�̈�_�v�́C���C���C���̍��W�Ŏw�肵�܂��D ��̎��̂悤��D��ς͏ꏊ���Ƃɒl���ς����̂��Ƃ������ƁC�܂��u�ʒu�̊��v�ɂȂ��Ă��邱�Ƃ�����ƁC �Ȃ�ƂȂ��P�_���w�肵�Ă��銴�����o�܂��D
�i�������C�����܂ŏo�Ă���E��D���S�Ĉʒu�̊��ł����C�����S�`���S�`������̂Ŗ������Ă��܂���ł����D ���ꂩ����ȗ����܂����C������Ə����Ώ�̎��̂悤�ɂȂ�Ƃ������ƂŁD�D�D�j
�܂��́C�C���[�W���₷���d�ׂ̍��i�E�Ӂj������t���܂��D�g�ρh�Ƃ�����ł��D
�u�����`�v�͋�ԏ�̂P�_�Ɋւ��b�Ȃ̂ŁC�d�ׂ̂ق�����ԓI�ɍׂ����o�����āg�_�h�ƌ�������x�̑傫���ɂ��Ă����܂��D �N�[�����̖@���Ȃł́u�_�d�ׁv�Ƃ������ƂŁC�T�C�Y���[���i�_�j�̓d�ׂ�z�肵�Ă��܂������C �����̓d�ׂ͕��ʂ́u�����v�Ȃ̂ŁC�K��������x�̑傫��������܂��D
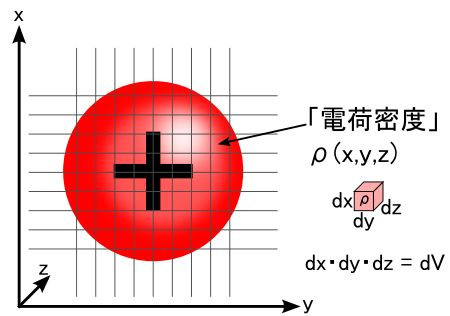
��̐}�̂悤�ɁC�d�ׂ��ׂ����}�X�ڂŐ蕪���܂��D ���̐蕪�����P���̃u���b�N�Ɋ܂܂�Ă���d�ׂ̗ʂ��C�P�ʑ̐ς�����̓d�חʂƂ������Ƃ��d�ז��x�ƌĂт܂��D�L���̓ρi���[�j�ł��D �������ۂ��l����������ƁC���̐蕪����}�X�ڂ̑傫�����Ɍ��܂ŏ���������C �u����P�_�ɂ�����d�ז��x�ρv�ɂȂ�܂��D �d�ז��x�̎�����[C/m3]�ł��D
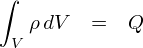
���̓d�ז��x�ς��C�d�ו��z�����݂���S�̈�Őϕ�����C���R�ł����蕪����O�́g�S�̂̓d�ח�Q�h�ɂȂ�܂��D ���̐ϕ��́C�u�P�ʑ̐ς�����̓d�ז��x�ρv�Ɂu�P�ʑ̐�dV�v�������āC�S�̈�Ɋւ��Ăǂ�ǂ��Z���Ă����C���[�W�ł��D ���̑���͂��̂܂���u�̐ϕ��v�ƌĂ�Ă��܂��D �ϕ��ϐ���dV�́gV�h�Ȃ킯�ł����C�����Ƒ̐�V�iVolume�j��V���Ǝv���܂��D
��̎����C�O�ɍ�����u�K�E�X�̖@���i�ϕ��`�j�v�ɑ�����Ă݂܂��D
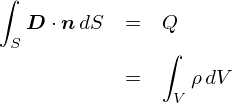
�gQ�h�̕�����d�ז��x�̑̐ϕ��ɏ��������܂����D �Ƃ肠�������ɏo�Ă���̂��d�����xD�Ɠd�ז��x�ς����ɂȂ��āC ������ۂ��i�H�j�����ł��D ���ǂ��ł����C���ӂ̓d�ז��xD�́u�ʖ��x�v�Ȃ̂ɑ��āC�E�ӂ̓d�ז��x�́u�̐ϖ��x�v�ł��D ����Ȃ킯�ł��ꂼ��ʐϕ��Ƒ̐ϕ��Ƃ������ƂɂȂ��Ă܂��D
���ɁC�d��i�d�����x�j�̕��Ɏ��t���܂��D���ӂ́g�ށED�h�Ƃ�����ł��D
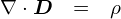
�u�ϕ��`�v�̘b�̎��́C�g�ȖʑS�̂ɂԂ���d�C�͐��̑��{���h���C���[�W���邱�ƂŘb��i�߂Ă��܂����D ����́u�����`�v�Ȃ̂ŁC�g�����_����o��d�C�͐��̖{���h���l���邱�ƂɂȂ�܂��D
�g��_�h�ƌ����Ă��C�����̓_��d�C�͐����ʉ߂���C���[�W�͓���i�d�C�͐��́g�ʁh���ђʂ���C���[�W�j�̂ŁC �ŏ��͓_�ł͂Ȃ��u�����̐ρv���l���闬��ɂ��܂��D �����������o���Ƃ��̏퓅��i�ł��D�D�D
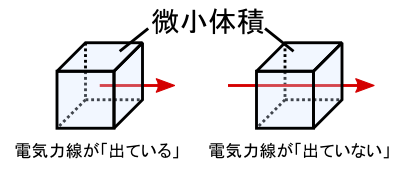
��̐}�ł́C�����̐ς���d�C�͐����u�o��v���̃C���[�W�ƁC �����̐ς���d�C�͐����u�o�Ȃ��v���̃C���[�W���r���Ă��܂��D �u�o�Ȃ��v���́C�d�C�͐��������̐ς��ђʂ��Ă��邾���ł��D �����̐ς̑O��œd�C�͐��̗ʂ͕ω����܂���D ����ɑ��āC�u�o��v���͔����̐ς̑O��œd�C�͐��̗ʂ������Ă��܂��D ����ƁC �u�����̐ς̑O�����ׂ�Δ����̐ς���o��d�C�͐��̗ʂ�\����̂ł́H�v�Ƃ����C�����Ă��܂��D ���������̐ς���d�C�͐����o�Ă���Ȃ�C�����̐ς�ʉ߂���O��œd�C�͐��̖{���������Ă���͂��ł��D
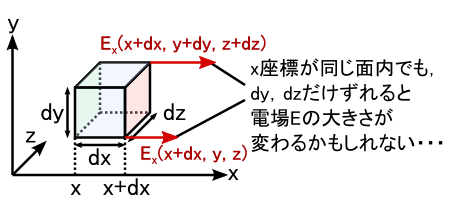
�����ŕ\�����߂ɁC�����̐ς����W�ɏ悹�܂��D ��������́C�ȒP�̂��߂ɂ������̓d��gEx�h�������l���܂��D �i�d��̓x�N�g���Ȃ̂�E�iEx, Ey, Ez�j�Ƃ��������łR�����������Ă��܂��D�j
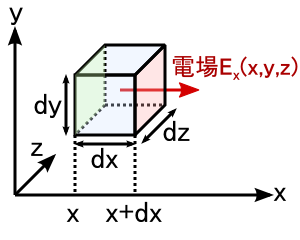
�����̐ς̊e�ӂ̒����́Cdx�Cdy�Cdz�Ƃ��܂��D ��̐}�̒ʂ�C�d�C�͐����ʉ߂���u�O�v�̖ʂ̖͗ʁi���W�͂��j�ŁC �d�C�͐����ʉ߂����u��v�̖ʂ͐Ԃ��ʁi���W�͂��{�����j�Ƃ������ƂɂȂ�܂��D �̖ʁC�Ԃ��ʁC�Ƃ��ɖʐς�dy�Edz�ł��D
�����ŁC�d��E�́u�d�C�͐��̖��x�v�Ȃ̂ŁC�g�d��~�ʐρh�ł��̖ʂ�ʉ߂���d�C�͐��̖{�������܂�܂��D ����āC�̖ʂ�ʉ߂���d�C�͐��̖{���́gEx�i���C���C���j�Edydz�h�ŁC �Ԃ̖ʂ�ʉ߂���d�C�͐��̖{���́gEx�i���{�����C���C���j�Edydz�h�ƕ\���܂��D
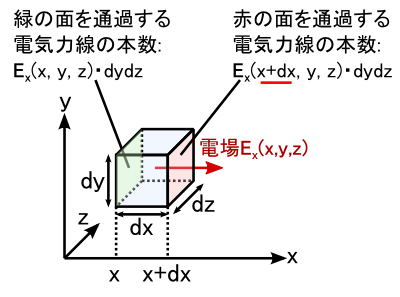
����ƁC�����̐ς̑O��ł��d�C�͐��̑������C �܂�C���߂��������u�����̐ς���o��d�C�͐��̖{���v�́C �P���ɐԂ̖ʂ���̖ʂ������Z������܂�܂��D
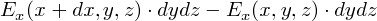
��̎��ŕ\�����ʂ����ɂȂ鎖�����邩������܂��C���̏ꍇ�́u�d�C�͐����z������ł�v�Ƃ������ƂɂȂ�܂��D ����͒P���Ɍ����̖��ŁC���̓d�ׂ̏ꍇ������ɂ�����܂��D
�����܂ł́g�ʁh���ӎ����₷���悤�ɁC�����̂̌`�������u�����̐ρv���g���čl���Ă��܂����D ���ǂ��ł����C���̔����̐ς͂����܂Łg�_�h�̃C���[�W�̑���ł��D ��́u�����̐ς���o��d�C�͐��̖{���v�̎��ł͔����̐ρidV=dxdydz�j�̌`�������Â炭�Ȃ��Ă���̂ŁC �gdxdydz�h�̐ς̂����܂��������o���Ă����܂��D
�����Z�̕����̕���Ɂg�����h�����āC�������gdxdydz�h�̂����܂�����܂����D �gdxdydz�h�𗧕��̂̔����̐ρgdV�h�ɏ����ς��Ă����܂��D
�����ŁC��̎��ŐԂ��A���_�[���C���������������́C �u�d��E�i���C���C���j�Ƃ����R�����������ɂ��āC�Ƃ肠�����������������l���ĕω������v�Z���Ă��������v�Ƃ����`�C �܂肘�������u�Δ����v�̒�`���̂܂�܂ɂȂ��Ă��܂��D
�d��͂��Ƃ���E�i���C���C���j�Ƃ����R�ϐ����Ȃ̂ŁC���������W�������Ƃ��Ă��C �����ʐρgdydz�h�̒��ł����W�ₚ���W���Y����Ɠd��E�̑傫�����ς���Ă��܂���������܂���D ����Ȃ�C�Ƃ肠�����d��E�̂����������C�ɂ��Čv�Z���Ă����Ηǂ����낤�E�E�E�Ƃ����C�����ŕΔ������o�Ă��܂��D
����Ȃ킯�ŁC�Δ����̌`���g���C�������́u�����̐ς���o�Ă���d�C�͐��̖{���v��\���ƁC�ȉ��̂悤�ɂȂ�܂��D
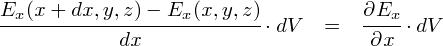
���������܂Ƃ܂����`�ɂȂ��Ă��܂����D
�����܂ō���������{�����u�������֏o�Ă����d�C�͐��̖{���v�ɂȂ��Ă���Ȃ�C �t�����i�����̃}�C�i�X�����j�֏o�Ă����d�C�͐��ɂ��Ή����Ă���͂��ł��D ������Ɗm�F���Ă����܂��D
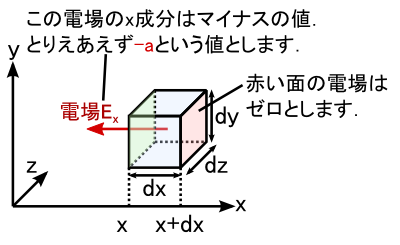
�܂��C�u�����̃}�C�i�X�����֓d�C�͐����o�Ă����v�Ƃ����Ȃ̂ŁC ���̓d��E�̂������͓��R�}�C�i�X�̒l�ɂȂ�܂��D �v�Z�Ɏg���d��̋����́C�K���Ȓl�Ƃ������ƂŁC�Ƃ肠�����̖ʂł́g-a�h�Ƃ��܂��D �܂��C�v�Z���ȒP�ɂ��邽�߂ɁC�Ԃ��ʂł͓d��̑傫�����[�����Ƃ��܂��D ���̏Łu�����̐ς���o�Ă����d�C�͐��̖{���v���v�Z���Ă݂�ƁC���̂悤�ɂȂ�܂��D
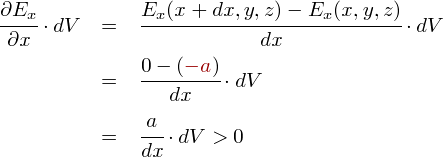
�v�Z�̌��ʁC�v���X�̒l���o�Ă��܂����D����Ȃ킯�ŁC�v���X�̌������낤�ƃ}�C�i�X�̌������낤�ƁC �����̐ς����u�o�Ă����v�d�C�͐��̖{����������ƕ\���Ă��鎖���m�F�ł��܂����D
���ǁC�������ɂ��Ă��u�����̐ς���o�Ă����d�C�͐��̖{���v�����̎��ŕ\���܂��D
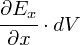
�����܂ł�������������ɂ��čl���Ă��������C���̂܂܂������C�������ɑ��Ă��K�p���܂��D �������Ƃ��J��Ԃ������Ȃ̂ŏȗ����܂����C���ǁg���h�Ə����Ă��镔�����g���h��g���h�ɏ��������邾���ɂȂ�܂��D ����Ȃ킯�ŁC�������C�������Ɍ������āu�����̐ς���o�Ă����d�C�͐��̖{���v�͈ȉ��̂悤�ɂȂ�܂��D
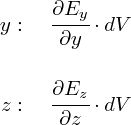
�ł́C�����̐ς���g�S�����֏o�Ă����h�d�C�͐��̖{�����v�Z���܂��D �b�͊ȒP�ŁC����܂ō���Ă����������C�������C�������̎���S�������Z���邾���ł��D
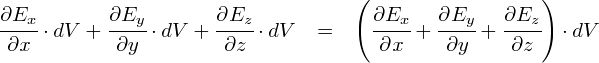
��̎����C�u�����̐ς���o�Ă����d�C�͐��̖{���v�̎��ƂȂ�܂��D
���Ƃ́C�����܂ŗp�ӂ��Ă����u�����̐ϓ��̓d�ׁi�d�ז��x�j�v�Ɓu�����̐ς���o�Ă����d�C�͐��v�����т����Ƃ���邾���ł��D
�����ŁC���ɍ���Ă������ϕ��`�̃C���[�W���g���āC���܂������`�̎����܂Ƃ߂��Ȃ����l���Ă݂܂��D
�d�ז��x�ς�d��Q�͈̔͑S�̂ő̐ϕ�����ƁC�S�̂̓d��Q��������̂ł����D ����Ɠ����悤�ɁC�u�d�C�͐��v�ɂ��Ă����ׂĂ͈̔͂Ŕ����̐ς��o�����̂𑫂��Ă����C��͂�d��Q�S�̂��o���d�C�͐��̖{���ƈ�v�������ȋC�����܂��D ���������Ȃ�u�d�ׁv�Ɓu�d�C�͐��v�̂��ꂼ��ɂ��āC�����`�Ɛϕ��`�̘b���Ȃ��邱�ƂɂȂ�܂��D
����Ȃ킯�ŁC�����̐ς��ǂ�ǂ��Ă����ƁC�O�֏o�Ă����d�C�͐��͂ǂ�Ȋ����ɂȂ邩���Ă݂܂��D
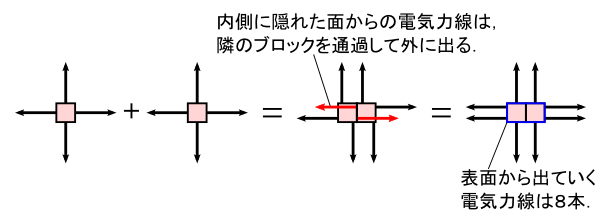
��̐}�ł́C�P�̔����̐ς���͂S�{�̓d�C�͐����o��Ƃ��Ă��܂��D ���̔����̐ς��Q�p�ӂ��Ă������܂��D �d�C�͐��̑��{���́C���R�ł����C �����̐ς̐������d�C�͐��𑫂��Z��������̂łW�{�ł��D �Q�̔����̐ς��ڂ���ʂ͓����ɉB��Ă��܂��܂����C ��������o�Ă����d�C�͐��ׂ͗̔����̐ς�ʉ߂��Č��NJO�֏o�Ă������ƂɂȂ�܂��D ����ƁC������������\������o�Ă����d�C�͐����C��͂�W�{�ƂȂ�܂��D
�����ŁC�u�\�ʂ���o�Ă����d�C�͐��̑��ʁv�Ƃ����̂́C �ϕ��`�̘b�ŏo�Ă����u�d��E�̖ʐϕ��v�̂��Ƃł��D ������u�����̐ς���o�Ă����d�C�͐��́g�̐ϕ��h�v����v���Ă���킯�ł��D �����ŕ\���Ǝ��̂悤�ɂȂ�܂��D
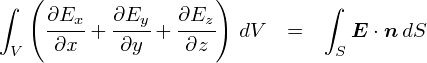
���ǂ��ł����C��̎��́u�����̐ς��Ƃ̓d�C�͐���̐ϕ��������́v���u�d�ׂ̊O�����͂ޕȖʂɂԂ���d�C�͐���ʐϕ��������́v�� ��v����Ƃ������ł��D ���ӂ͑̐ϕ��C�E�ӂ͖ʐϕ��Ƃ������ƂɂȂ��Ă���킯�ł����C ���̎��͓d��̘b�Ƃ͕ʂɁC�̐ϕ��Ɩʐϕ���ϊ���������Ƃ��ďd��炵���ł��D �u�K�E�X�́g�藝�h�v�ƌĂ�邻���ł��D�D�D
�ϕ��`�ō���Ă����������C�����܂Ŕ����`�̗���ō���Ă������ƂȂ���܂����D ����ŁC�u�����`�̃K�E�X�̖@���v�̏d�v�ȕ����͂��������I���ł��D
�����܂ł̘b�ŁC�u�d�ׁv�Ɓu�d�C�͐��̖{���v�̗����Ƃ��C�����`�Ɛϕ��`�̌`���Ȃ���܂����D
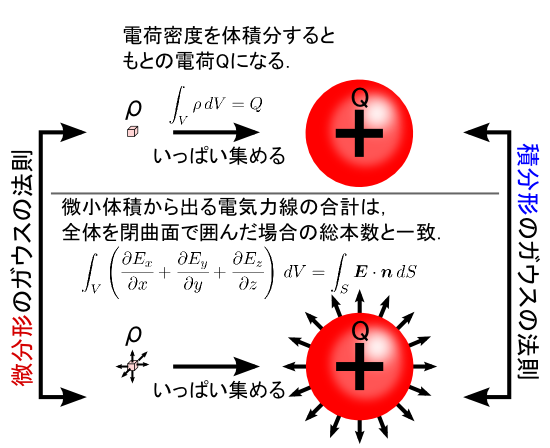
�����ŁC�O�ɍ���Ă������u�ϕ��`�̃K�E�X�̖@���v�͈ȉ��̎��ł����D �u�d��Q����o�Ă����d�C�͐��̖{����Q/��0�v�Ƃ�����ł��D
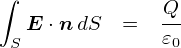
��̎��̍��ӂ��C��������`�̗���Ŏ����Ă����u�����̐ς���o��d�C�͐��̑̐ϕ��v�Œu�������܂��D
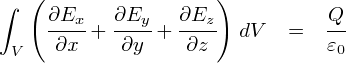
�����ŁC�d��Q�Ƃ����͓̂d�ז��x�ς̑̐ϕ��ł����D
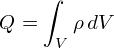
��̎����g���āCQ�̕������ς��g�������ɏ��������܂��D
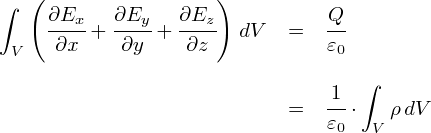
��0�𗼕ӂɂ����Z���āC�ȉ��̎����ł�������܂��D
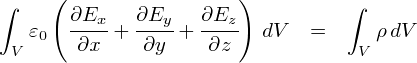
��̎��̗��ӂ�����ׂ�ƁC�ǂ�����̐ϕ��̌`�ɂȂ��Ă��܂��D �̐ϕ����ăC�R�[���ɂȂ�Ƃ������Ƃ́C �̐ϕ�����O�̒l�������ɂȂ��Ă���͂��ł��D �Ƃ����킯�ŁC�ϕ�������Ƃ��ς���Ē��g�����̎��ɂ��܂��D
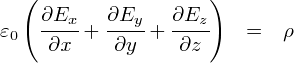
���ꂪ�C�u�d��Ɋւ���K�E�X�̖@���i�����`�j�v�Ƃ�����ł��D �C���[�W�Ƃ��ẮC�����ȋ�ԁi�قځg�_�h�ƌ����Ă��ǂ��j�ɂ���d�ז��x�ς���o�Ă����d�C�͐��̖{���́C �d��E�̂��C���C�������ւ̕ω�����S�đ��������̂��E�E�E�Ƃ��������ł��D
��̂��Ƃ��C�d��ƗU�d���̐ς̌`���o�Ă��Ă��܂��D �傫�ȓd�ׂ̂����܂肾�낤�ƁC�P�ʑ̐ϓ�����̓d�ז��x�ς��낤�ƁC �P�N�[����������P�{���u�d�����v���o�Ă���͓̂����ł��D �d�����̗ǂ����́C�u�d�ׂ̗ʂ����Ɉˑ����āC����̔}���ɉe�����Ȃ��v���Ƃł����D ���������̔}���ɍ��E����Ȃ��g�����h����肽���̂ŁC�d�����x�����邱�Ƃɂ��܂��D
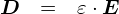
��̒�`���g���āC�����`�̃K�E�X�̎��������Ȃ����Ă����܂��D
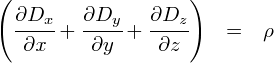
���ǂ��ł����C��̎��̈Ӗ��́u�d�ז��x������ƁC�d�����i�d�C�͐��j�̗ʂ���ԓI�i���C���C�������Łj�ɕω�����v�Ƃ������̂ł��D �v�́C�d�ׂ���d�C�͐����o�Ă�����C�ł��D
��������́C�ʂɖ{���I�ł͂Ȃ��̂ł����C���̌`���Y��ɂ��悤�Ƃ�������ł��D
�܂��C�u�x�N�g���̓��ρv�Ƃ�������m�F���Ă����܂��D �Ƃ肠�����K���ȂR�����x�N�g��A��B��p�ӂ��܂��D
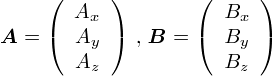
�����́u���ρvA�EB�́C�x�N�g���̐������g���Ď��̂悤�Ɍv�Z����̂ł����D
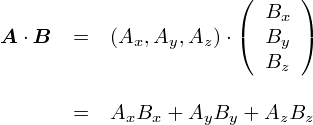
�܂������`�̃K�E�X�̖@���֘b��߂��܂��D �d�����x��Δ�������Ƃ���ł����C��������u�Δ������Z�q�̃x�N�g���v�Ɓu�d�����x�̃x�N�g���v�Ƃɕ������܂��D
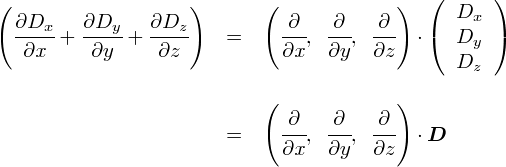
�����ŁC��̎��ł�����o�����u���C���C���������ꂼ��̕Δ������Z�q�̃x�N�g���v�� �i�u���ƌĂ��L���ނŕ\�������ł��D �ǂ����āC�킴�킴�i�u���Ȃ�Ă��̂�p�ӂ��邩�Ƃ����ƁC ���́u�Δ������Z�q�̃x�N�g���v�Ƃ����̂́C����̘b�̑��ɂ��l�X�ȃV�`���G�[�V�����ŏo�Ă��邩��ł��D �F�X�ƕ֗��Ȃ�ł��D
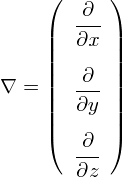
����ƁC���Ƃ��Ƃ̎��̓i�u���Ɠd�����x���g���Ĉȉ��̂悤�ɕ\���ł��܂��D
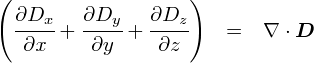
�ŁC�����`�̃K�E�X�̖@���͈ȉ��̂悤�Ȏ��ł����D
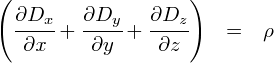
��̎����C�i�u�����g���ĕ\���ƁC���̎��ɂȂ�܂��D
���Ȃ�X�b�L���܂Ƃ܂�܂����D �������肵�����Ȃ̂ŁC�����`�̃}�N�X�E�F���������̑�P���Ƃ��Ă悭�Љ��܂��D �����₷���ł����D�o���₷���̂ŁD
�����ŁC�g�ށED�h�̕����̂��Ƃ��Ƃ̈Ӗ����v���o���ƁC ����́u�d�����������̐ς���o�Ă����ʁv�Ƃ��������ł����D ���̃C���[�W����C�i�u���Ɠ��ς���邱�Ƃ��u���U���v�Z����v�ƌ������肵�܂��D �d�C�͐��i�d�����j�́u���U�v�Ƃ����̂́C�N���o���Ƃ������C��яo���Ƃ������C�Ȃ���Ȋ����ł��D �u���U�v�͉p��Łgdivergence�h�i�_�C�o�[�W�F���X�j�ƌ����킯�ł����C ����𗪂��āgdiv�h�Ə������肵�܂��D

��̎��́C���ǁu�i�u����D�Ƃ̓��ς��v�Z����v�Ƃ����Ӗ��Ȃ̂ł����C ���Ɂu���U�v�̌v�Z�̃C���[�W���ł��Ă���l�ɂƂ��Ắgdiv D�h�Ə������ق����C �����I�ɉ����Ӗ����Ă���̂������ɕ�����̂Ŋ������E�E�E�炵���ł��D
�����܂Œ��X�ƍ���Ă��������`�̎��ł����C���ۂɓd����������͂��܂�g���܂���D �����C���̎����������ƕό`�����u�|�A�\���������v�Ƃ����͓̂d��̉�͂ł₽��Ƒ��p���܂��D �������̕����֗�������ł��D �i�|�A�\���������́C�����̂̒��̓d�ʕ��z���l���鎞�ɏo�Ă��邩������܂���D�Ƃ肠�������̓X���[���܂��D�j
�ȏ�Ń}�N�X�E�F���������̑�P���̘b�͏I���ł��D
�}�N�X�E�F���������̂Q�߂́C�u����̌`�v�̘b�ɂȂ�܂��D
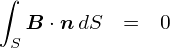
���ӂ̖ʐϕ��́C��P���̓d��Ɋւ���K�E�X�̖@���Ɠ����C���[�W�ł��D ���̎��ł́C���̖ʐϕ��̒l����Ƀ[���ɂȂ��D�D�D�ƌ����Ă��܂��D ����͂ǂ��������Ӗ��Ȃ̂��C�l���Ă݂܂��D
����͐���������e�����܂肠��܂���D�D�D�������鍀�ڂ͂P�_�����ł��D
�Ȗʂ��C���[�W���Ėʐϕ�����b�́C�u�d��Ɋւ���K�E�X�̖@���v�ŎU�X�o�Ă�����ł��D ������ƕ��K���C�ǂ�ȏȂ�Ȗʂł̖ʐϕ����[���ɂȂ肻�����l���Ă݂܂��D
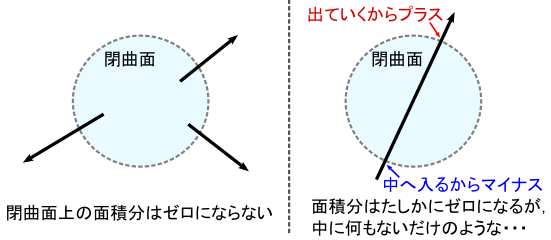
�܂��C���ʂɕȖʂ̒�����O�փx�N�g�����o�Ă���悤�ȏ�ł́C �ǂ�ȂɃx�N�g���������������Ƃ���Ŗʐϕ��̒l�̓[���ɂȂ�܂���i���}�j�D �ł́C�E�}�̂悤�ɕȖʂ��P�{�̃x�N�g�����ђʂ���悤�ȃC���[�W�����Ă݂܂��D ���̏ꍇ�͕Ȗʂɑ��āu����ʁi�}�C�i�X�Ƃ��ăJ�E���g�j�v �Ɓu�o��ʁi�v���X�Ƃ��ăJ�E���g�j�v�������Ȃ̂ŁC �ʐϕ��̌��ʂ̓[���ɂȂ�܂��D ���������ꂾ�ƁC���������u����������ꏊ�v��Ȗʂň͂����Ƃ��Ă��Ȃ������̂悤�ȋC�����܂��D�D�D
�����Ɓu���ɉ���������v�ꏊ�Ȃ̂ɁC�Ȗʂň͂�Ŗʐϕ�����ƃ[���ɂȂ���l���Ă݂܂��D
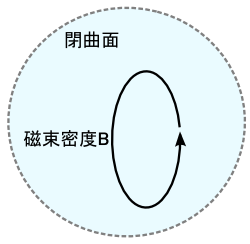
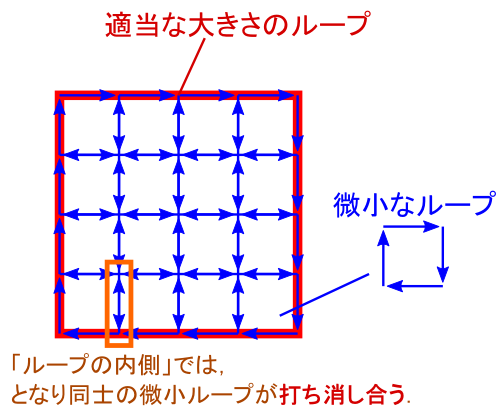
��̐}�̂悤�ɁC�x�N�g���������Ă��C���̃x�N�g�����ǂ�ǂ�Ȃ����Ă����Ď����̍��{�ɓ����Ă����悤�Ȍ`�ł���C �u�Ȗʂň͂������̖ʐϕ����[���v�Ƃ������ʂɂȂ�܂��D �܂�C�x�N�g���ꂪ�P�̃��[�v������Ă���ꍇ������̘b�ɓ��Ă͂܂�܂��D
����́C���w�Z�⍂�Z�ŏK���u�E�˂��̖@���v�̌`�Ɠ����ł��D ���̂悤�Ȍ`�́C���[�v����悤�Ȋ����̏���u�Q��i�����j�v�ƌĂԂ炵���ł��D
�u�Q��v�ɑ��āC�d�ׂ���d�C�͐����o��C���[�W�̓d��̂悤�Ȍ`���u���U��v �ƌĂԂ����ł��D���̃}�N�X�E�F���������̑�Q���������Ă���̂́C �u����͕K���Q��ɂȂ��Ă���v�Ƃ��������ɂȂ�܂��D
�d�C�Ɋւ���u�d�ׁv�̎��C�o�[�W�����Ƃ��āC�������u���ׁv�̂悤�Ȃ��̂�����C �d��Ɠ����m���Łg���ׁh����g���͐��h���o�Ă����悤�Ȏ��ꂪ�ł���͂��ł��D �������C���̑�Q���́u����Ȃ��Ƃ͂��蓾�Ȃ��v�ƌ����Ă��܂��D ����́C�u�P���ׁiN�ɂ̂݁CS�ɂ݂̂̎��݂����Ȃ��́j�͑��݂��Ȃ��v�Ƃ������ƂɂȂ�܂��D ����܂ł����Ȑl���T�����炵���̂ł����C������������Ȃ����������ł��D
����ƁC�u���ׂ������Ȃ�C������������́H�v�Ƃ����^�₪���R�ƗN���܂��D ����ɓ�����̂��C��ŏo�Ă����}�N�X�E�F���������̑�R���ł��D
�}�N�X�E�F���������̂Q�߁C����Ɋւ���@���́u�����`�v�ł��D
�����ϕ��`�̂Ƃ���ŏd�v�ȓ��e�͂قƂ�Ǐ����Ă��܂��܂����D ���ɏ������Ƃ�����܂���D�����`�ł��D

�Ƃ肠�����C�u�Q�������̐ςɕ�������v�C���[�W�����܂��D ����ƁC�ǂ̔����̐ς��u���͐����ђʂ��邾���ő�������������Ȃ��v�̂ŁC �P�P�̔����̐ς���V�������͐����o�邱�Ƃ͂Ȃ��E�E�E�܂莥��́u���U�v�̓[���C�Ƃ����C���[�W�ł��D �����D
���́ށEB�Ƃ����͕̂K���[���ɂȂ�̂ŁC ��X�d���g�̎��������鎞�Ɂu�ށEB�̓[���Ȃ��瑫���Ă������Ă������ł���H�v �Ƃ��������œˑR���̒��ɕt���������肷�邱�Ƃ�����܂��D ���ό`�ł悭�g����e�N�j�b�N�������肵�܂��D
�ȏ�Ń}�N�X�E�F���������̑�Q���̘b�͏I���ł��D�D�D
�}�N�X�E�F���������̑�R���ł��D �Ƃ肠�����C�u�d���i�Ƃ��j������������v�Ƃ������ł��D
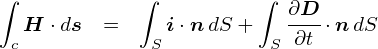
���ԂŕΔ������鍀�������Ă���̂ŁC �����������g���ԁh���ӎ����Ȃ�������Ȃ��悤�ł��D ���Ԃ̗��ꂪ�W����Ƃ������Ƃ́C��ɃV�[���Ƃ��Ă����ł͂Ȃ��āC�E�l�E�l�Ɓi�H�j�ω��������C���[�W���銴���ɂȂ�܂��D ����Ȃ킯�ŁC���ɏo�Ă���̂́u���(x, y, z)�v�Ɓu����(t)�v�̊��ł��D���������ƁC���̂悤�Ȋ����ɂȂ�܂��D
�����Ə����Ώ�̂悤�ȃC���[�W�ɂȂ�킯�ł����C �����S�`���S�`�����Č��Â炢�����ł��D ��̂��Ƃ��C����͏ȗ������`�ŏ����܂��D�D�D
���āC����́u��R���v�͐����̓��e��������Ƒ����Ȃ��Ă��܂��D�D�D �S�̂̃{�����[�����ӎ����C�u���͉������C���ɍl����́H�v�Ƃ����g���ݒn�h��c�����Ă����Ȃ��ƁC ���q�ɂȂ��Ă��܂���������܂���D �������ɂ��čl���Ă����܂��D
����̎�����u����v�ł��D���������R���͉��Ȃ̂��H�Ƃ����b����n�߂܂��D
���������g��h�Ƃ����̂́C�u���̂ɗ͂��͂��炭��ԁv�݂����Ȃ�ł����D �͂��͂��炭�̂ŁC��̒��ɂ��镨�̂́i����Ɂj������邱�ƂɂȂ�܂��D �u�d��v�̘b�ł́C������ӎ����āu�́v�̘b����o�����܂����D �u�d�ׂɂ͂��炭�́v�� �u�N�[�����̖@���v�� �u�d��v�� �u�K�E�X�̖@���v...�Ƃ�������ł��D �Ώۂɂ͂��炭�u�́v���S�Ă̏o���_�ł��D
����́u�����v�ł����̗����^�����āC�����p�^�[���Ɏ������߂�Ɗy�ł��D ���Ȃ킿�C�g�d�ׁh�ɑ��āg�����h�Ȃ�Ă̂�z�����āC �u�܂��́g���ׁh�ɂ͂��炭�͂ɂ��āD�D�D�v�Ȃǂƍl����̂��f���ȂƂ���ł��D �������Ȃ���C��Q���̂Ƃ���ŏo�Ă����悤�ɁC ���ۂɂ��u�P���ׂ͖����v�Ƃ������ƂɂȂ��Ă��܂��D �d��̏ꍇ�Ɠ�������Řb��i�߂�͓̂�����ł��D�D�D
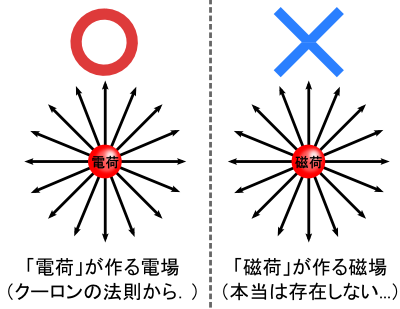
�����ł͓d��̘b�͈�x�Y��邱�Ƃɂ��āC �C�`���玥��̘b��g�ݗ��Ă܂��D
���āC���ׂ͖����炵���̂ŁC�l����g���m�h�Ƃ��Ďv�����̂́u�d�ׁv��������܂���D ���́u�d�ׂɂ͂��炭�́v�Ƃ����̂́C������P���̓d��̘b�ŕЕt���Ă��܂�����������܂��D�D�D �Ƃ��낪�C���̓d�ׂ��u�����v�ƁC�d�ꂾ���ł͈����Ȃ��b���o�Ă����肵�܂��D �d�ׂ���������C���Ȃ킿�u�d���v�ɂ͂��炭�͂ɂ��čl���Ă݂܂��D
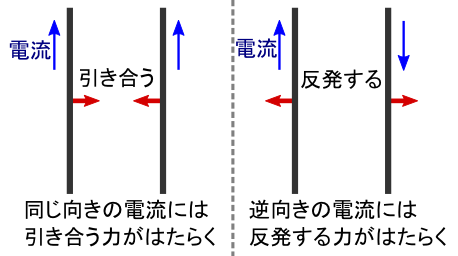
��̐}�̂悤�Ɂu�d���v�i���ۂ́u�d���v�ł����D�D�D�j���Q�{���ׂ����̂��C���[�W���܂��D ���̎��C�Q�{�̓d���̊Ԃɂ͗͂��͂��炫�܂��D �i�ǂ�ȋ��ȏ��ɂ������Ă��邨�Ȃ��݂̎������Ǝv���܂��D�j
�Q�{�̓d�������������̎��͓d�����m�����������͂��͂��炫�C �d�����t�����ɗ����Ɣ������܂��D �����ŁC�u�ǂ����Ă����Ȃ�́H�v�Ƃ������Ƃ��l���Ă݂܂��D �d�����u�v���X�̓d�ׂ��������́v�ƍl����ƁC�v���X�̓d�ד��m�͔�������͂��ł��D �������C��̎����ł́g���������h�̓d�������������Ă��܂��D �d��̃C���[�W�ő����悤�Ƃ���ƁC�Ȃ��悭������܂���D�D�D ���̎������ʂ̏d�v�ȂƂ���́C�u�N�[�����̖@���ł͐����s�\�v���Ƃ����Ƃ���ł��D ����Ȃ킯�ŁC�̂̃G���C�l�B���u�d���̎���ɂ́C�d��Ƃ͈Ⴄ�g�����h������v �ƍl����悤�ɂȂ��������ł��D
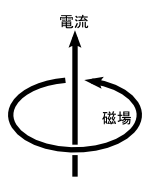
�����ŁC ���w�Z�⍂�Z�ł��Ȃ��݂́C�u�d���Ǝ����g���������v���C���[�W���܂��D ���̋߂��œd���𗬂��ƁC�d���ɑ��Ď������܂��������֓����i���H�j���Ƃ��m�F�ł��܂��D
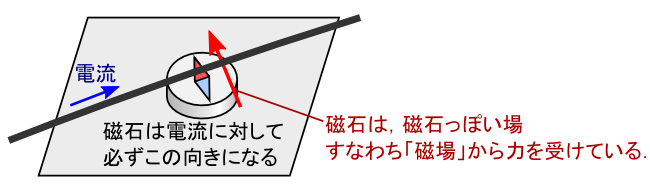
����������̂̐l�́C�d���̎���ɂł����͎��̗͂Ɠ�����ނ̕��Ȃ̂ł́H�ƍl�����炵���ł��D ����Ȃ킯�ŁC�����ۂ���C�u����v�iMagnetic Field�j�Ɩ��O��t���悤�D�D�D�Ƃ��������ɂȂ�܂����D
������Ƃ����ŁC�ƂĂ��d�v�Șb�������Ă����܂��D
�����܂ł̘b�ŁC����͊��S���u����v���Ƃ������͋C�ɂȂ��Ă��܂��D�D�D �������C���͂����ł͂���܂���D ���ׂĂ̍������C����̃��`�x�[�V�����́C �u���s�d���ɂ͂��炭�͂�����������v�Ƃ������Ƃł��D ���̃q���g��T�邽�߂Ɏ��������o���Ď����������̂ł����D �������u���v���̂��̂́C����͂����̘e���ł��D �u���������̂͂ǂ����āH�v�Ƃ��C�u�����������͂ǂ����Ď��Ȃ́H�v�Ƃ��C ���������b�͂܂��ʂ̓��e�ł��D �i�d�q�̃X�s���Ƃ��C�����_�̘b�Ɏ��˂����ނ��ƂɂȂ�܂��D ������ӂ̘b�́C�����ƌ�ŏ����܂��D�D�D�j
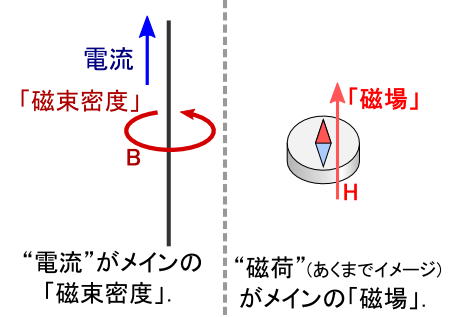
����̎���͂����܂Łu�d���v�C���̂Ƃ��Ă͓����Ă���d�ׂł��D �����āu�d���ɗ͂��͂��炭��v�͎�ɁC �u�������x�v (magnetic flux density)�Ƃ�������g���čl����̂ł����D �������x�̒P�ʂ��e�X���iT�j�ł��D ���̎������x�Ƃ�����́C�u�U���E�v(magnetic induction field) �Ƃ��Ăꂽ�肵�܂��D �i�{���I�ȃC���[�W���l����ƁC�u�U���E�v�̂ق���������₷�����t���Ǝv���܂��D�D�D���C ���{�̋��ȏ��̂قƂ�ǂɂ́u�������x�v�Ə����Ă���܂��D�j
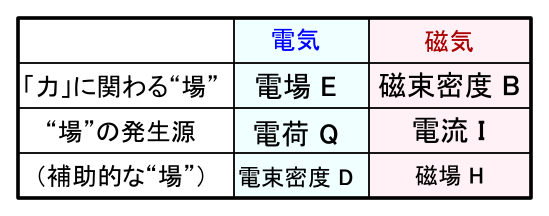
�Ƃ肠������̕\�̒ʂ�C�u�d��E�v�ɑΉ�����̂��u�������x B�v�Ƃ��������ɂȂ��Ă��܂��D �u���Ⴀ�C���̃��C���̏�i�������x�j�̂ق����g���� H�h�Ɩ��t����悩��������Ȃ����E�E�E�v �Ǝv���邩������܂���D �ǂ����Ă��Ȃ����̂��́C���j�̗��ꂪ���ޘb�ɂȂ�܂��D �̂̐l�́u���ׁv���{���ɂ���Ƃ����O��ŁC���C�̗��_��g�ݗ��ĂĐF�X�Ɩ��O��t���܂����D �������C���ۂɂ͒P���ׂ͑��݂��Ȃ����߁C ���݂̂悤�ȃ��C���̏�̕��Ɏ����g���x�h�Ȃ�Ė��O���t���悤�Ȋ����ɂȂ��Ă��܂��D�D�D
�Ƃ肠�����C�u�͂Ɋւ�郁�C���́g��h�́C�������x�Ȃv�Ƃ����������������Ă����Ă��������D ���� H�͉��̖��ɗ��́H�Ƃ����b�́C ��̕����o�Ă��܂��D
��̘b�ł́u����͓d���Ȃv�Ƃ������Ƃ��������܂������C ����ł́C�u���v�Ƃ����͉̂��҂Ȃ̂ł��傤���E�E�E�D
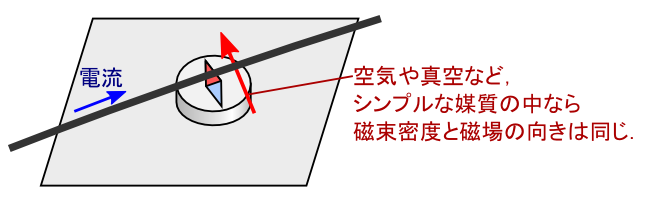
��₱�����Ƃ���ł����C���Ƃ�����͎��͂́u���� H�v����͂��܂��D�D�D �d��������́u�������x B�v�ł����C����Ɓu���� H�v�Ƃ͂ǂ������W�Ȃ́H�Ǝv���Ƃ���ł��D �����œd��̎��́C�u�d�� E�v�Ɓu�d�����x D�v�̊W���v���o���Ă��������D ����Ɠ����ŁC�Ƃ肠�������u�������x B �Ǝ��� H �͓����g��h������������Ō������̂��v �Ƃ��������łƂ炦�Ă����܂��D ����Ȃ킯�ŁC���͓d�������鎥�����x�ɂ�����Ɣ������Ă���܂��D ���ɁC��C���Ȃǂ̏ꍇ�͎������x�Ǝ���̌����͓����Ȃ̂ŁC �d������鎥�����x�̌����ׂ鎞�͎����g���Ă����C�ł��D
�i ���u���v�Ƃ����C���[�W�́C���������������̉~�`�d���i�d�q�̃X�s���C�d�q�̋O���^���j���C �����I�ɏ����Ȏ��C�o�Ɏq�ƌ��Ȃ������̂ł��D �u���v�̐��̂��~�`�g�d���h�Ȃ�C���R�C�������x����͂��܂��D �����ŁC�͂���{�̂́u�~�`�d���v�́C��Ɏ��i��ɓS�łł��Ă���j�̒��ɂ���܂��D ����ƁC�~�`�d�������ڐG�鎥�����x B = ��H�́g�ʁh�́C��Ɂu�S�̓������v���g�����ƂɂȂ�C���̍X�ɊO���ɂ���}���Ƃ͖��W�ł��D ���̂��Ƃ���C�~�`�d������́i= ������́j�́C ������������̔}���ɍ��E���ꂸ�������� H �̒l�݂̂Ɉˑ�����悤�Ɍ�����E�E�E�Ƃ��������ɂȂ��Ă��܂��D ���̗l�q���w���āC�u���͎������x�ł͂Ȃ����ꂩ��͂���v�ƕ\������炵���ł��D �{�����u�d���͎������x����͂���v�Ƃ����C�������ꂾ���̘b�ł��D �j
���āC�d���̎���ɂ́u�������x�v�������Ă���炵���ł��D �Ƃ肠�����C���[�W��c��܂��邽�߂ɁC����́u�`�v�Ɓu�����v�ׂĂ݂܂��D ���Ȃ��݂́C�d���̎���Ɏ���u���������C���[�W���܂��D
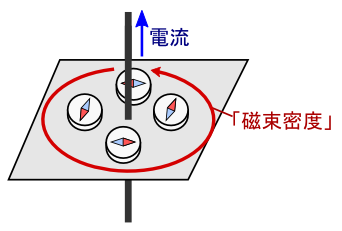
�d��������́C������ƃ��[�v����悤�Ȍ`�ƂȂ��Ă��܂��D ����́C�}�N�X�E�F������������Q���������Ă�����e�Ƃ��܂������܂��D
�d�������鎥�����x���u�`�v�͂�������������܂����D ���́C�u�����v�ׂ܂��D �P�ɁuN�ɂ��w���������������x�̌����ł������낤�v�Ǝv���Ƃ���ł����C ����������Əڂ������Ă݂܂��D �����ł́C�d�C�͐��Ǝ����������u���͐��v�Ƃ�������g���Ă݂܂��D ���Ȃ��݂̓d��ƁC�V�����o�Ă���������r���Ȃ���i�߂Ă����܂��D
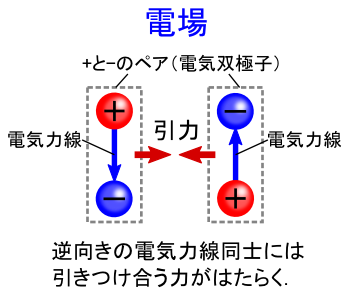
�܂��C���Ȃ��݂̓d��̕��ł����C �v���X�d�ׂƃ}�C�i�X�d�ׂ��y�A�ɂȂ��Ă�����̂��C���[�W���܂��D �g�d�C�o�Ɏq�h�Ƃ�����ł��D �i���ܓd�C�o�Ɏq�������o�����̂́C����̕��Łg���h�ƑΉ�������������ł� �D���ɂ́CN�ɒP�̂�S�ɒP�̂́u�P���ׁv�͑��݂��܂���D�K��N�ɂ�S�ɂ��y�A�ɂȂ��Ă��܂��D�j ���āC��̐}�̂悤�ɋt�����̓d�C�o�Ɏq����ׂ��l�q���C���[�W����ƁC �u�t�����̓d�C�͐��ǂ����͈��������v�Ƃ����������m�F�ł��܂��D
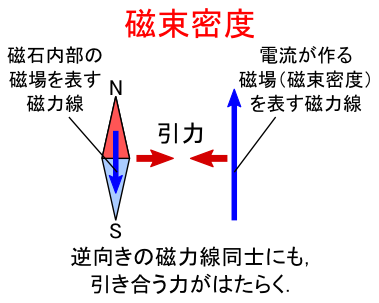
���Ɂu���͐��v�ł��D ���͐��͓d�C�͐��Ɠ����m���ŁC�u����N�ɂ���o��S�ɂɓ�����́v�ƌ��߂܂��D �����ŁC���͐����d�C�͐��Ɠ����悤���u�t�����̎��͐��ǂ����͈��������v �Ƃ�������������܂��D ����͎����đf���ȍl�������Ǝv���܂��D
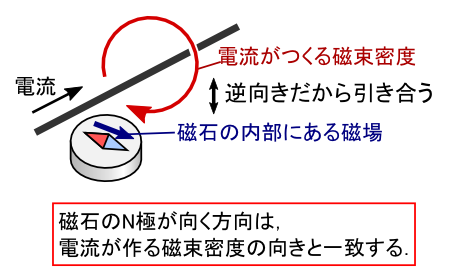
���ۂɓd���̋߂��Ɏ���u�������̗l�q�́C���̎��͐��̃C���[�W�Ő������������邱�Ƃ��ł��܂��D ���ǁC�u�d�������鎥�����x�̌����́C����N�ɂ��w������������Ε�����v�Ƃ������ƂɂȂ�܂����D ���X���ǂ������ł������C�ꉞ�O�̂��߂Ƃ������ƂŁD�D�D

���߂āC��̐}�����Ă݂܂��D �e�ꏊ�ɂ����鎥�����x�̌����́C�����ɂ��鎥��N�ɂ��w�������ł��D ����āC�d������鎥�����x�̌����́C���w�Z�ŏK���ʂ� �u�d�����i�ތ����ɑ��ĉE�l�W�������v�Ƃ������Ƃ��m�F�ł��܂��D �Ƃ肠�����C�d���̎���ɂ͂���Ȋ������u�Q��v���ł��Ă���Ƃ������ƂŁD
�ł́C�ŏ��ɏo�Ă����u���������ɗ����Q�{�̓d���v�̘b���m�F���Ă݂܂��D
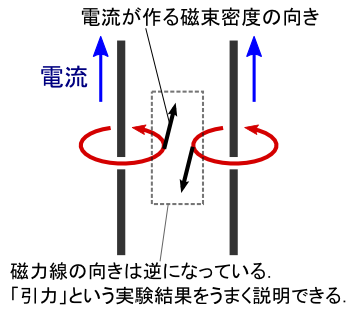
�u�d������鎥�����x�́C�d�����i�ތ����ɑ��ĉE�l�W�������v�Ƃ�������C ��̐}�œ��Ă͂߂Ă݂܂��D
����ƁC�Q�̓d���̓����ł͎��͐����t�����ɂȂ��Ă���̂ŁC �������u���������ɗ���镽�s�d���Ԃɂ́C���͂��͂��炭�v�Ƃ������ʂ����Ƃ��ł��܂����D �܂��C���炽�߂ēd������鎥�����x�́u�`�v�Ɓu�����v�͏�̃C���[�W�̒ʂ肾�ƍĊm�F�ł��܂��D
�����܂ł̘b�ň�ԑ�Ȃ��Ƃ́C �u�V���Ɂg�������x�h�����邱�ƂŁC�d�����m�ɂ͂��炭�͂�����ł����v �Ƃ������ł��D ���̎��������́C�d��Ɋւ���N�[�����̖@���ł͐�ɐ����ł��܂���D �g����h�������́g�������x�h�Ƃ�������l���āC���߂ċ̒ʂ����b���ł���悤�ɂȂ�܂����D
����ł́C��̓I���u�d�����������x�����́v ���l���邱�Ƃɂ��܂��D �g��̓I�Ɂh�Ƃ������Ƃ́C�����������āu���̂��炢�̑傫���v�Ƃ��\������K�v������܂��D �v�́C�����������o�����E�E�E�Ƃ������Ƃł��D
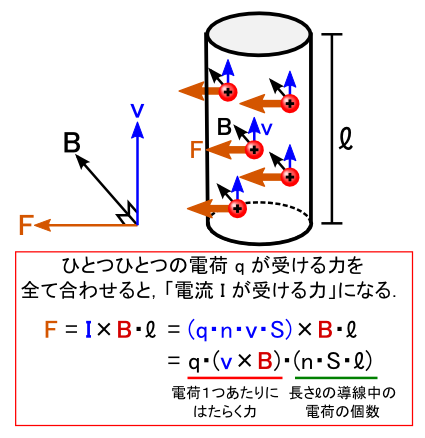
�܂��͗͂���Ώۂł����u�d���v�ɂ��āC�ڂ������Ă݂܂��D �d���Ƃ����͓̂d�ׂ̗���̎��Ȃ̂ŁC �{���Ƃ��Ă��u�����Ă���d�ׁv���C���[�W���邱�ƂɂȂ�܂��D ����Ȃ킯�ŁC�u�d�ׁv���ӎ����d�����~�N���Ȏ��_�Ō��Ă݂܂��D
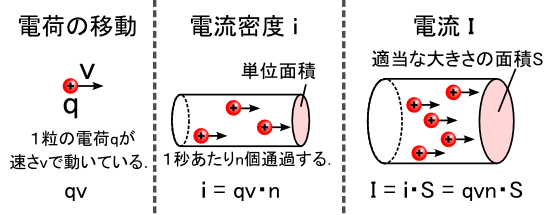
�܂��C�u�d��q�����xv�œ����Ă���v�Ƃ����C���[�W���������Ƃɂ���܂��i��}�C���j�D �����āC�d�C��ʂ������̒��ɂ͓d�ׂ������ς�����킯�ł����C ����ʂ��u�P�ʎ��ԁi= 1�b�j������ɒʉ߂���d�ׂ̐��v�̂��Ƃ��u�d���v �ƌĂԂ̂ł����i��}�C�E�j�D �L����I�C�P�ʂ�A�i�A���y�A�j�ł��D ���ɁC�d�ׂ��ʉ߂���ʂɂ��āC�u�P�ʖʐρv������ɒʉ߂���d�C�ʂ̂��Ƃ��u�d�����x�v �ƌĂ肵�܂��i��}�C���j�D �d�����x i �̒l�ɁC�K���Ȗʐ� S �������Z����ƁC�S�̂𗬂��d�� I �ɂȂ�܂��D
�d�����x�̕��z���ꏊ�ɂ���ĈقȂ�ꍇ�́C�u�ΏۂƂ���ʁv���l���Ėʐϕ����邱�ƂɂȂ�܂��D
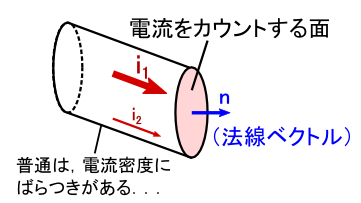
�d�����x i ��ʐϕ����đS�d�� I ���v�Z���鎞�́C�ʂɐ����Ȑ����������l���܂��D �ʂ�ʉ߂���u�����I�ȓd���v�Ƃ��������ł��D �����ŕ\���ƁC���̂悤�ɂȂ�܂� �i�������Ă��܂��C�d�����x i �͏ꏊ�ix, y, z�j�̊��ł��D �܂�C�d�����x i �͏ꏊ�ɂ���ĈႤ�l�ł�������E�E�E�Ƃ������Ƃł��j�D
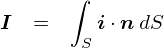
��̎��́C�u�P�P�̓d�ׂ̓����v�����v����Ɓu�d���v�ɂȂ��C �Ƃ����b�𐔎��ŕ\���������ł��D ���ǁC�������̘b���u�P�P�̓����Ă���d�ׂ͎��ꂩ��ǂ�ȗ͂���́H�v�Ƃ������ƂɂȂ�܂��D ���͂���ɂ��čl���܂��D
�ŏ��ɏo�Ă����u���s�d���ɂ͂��炭�́v���ނɂ��āC �d�ׂP�P�ɂ͂��炭�����ӎ����C������Ɛ��������Ă����܂��D
�Ƃ肠�������̐}�̂悤�ɁC�Q�{�̓������㉺�ɕ��ׂĂ����܂��D �܂��C���������₷���悤�ɁC���W(x, y, z)��~���Ă����܂��D ����́C��̓d�����u�������x�����鑤�v�C���̕����u�͂��鑤�v�Ƃ��܂� �i�㉺�����ւ��ē����b������C�݂��Ɉ����������Ƃ�����ł��܂��j�D
�������x�̒��ɂ���d���͗͂��܂��D ����́C�e�d������鎥�͐��̌������C���[�W���邱�Ƃʼn��߂��Ă��܂����D �u���͐��v�ǂ�������������E���������E�E�E�Ƃ����������ł��D ����ɑ��āC���x�̓��m�ɒ��ڂ��C�u�������x�̒��ł́C�����Ă���g�d�ׁh���͂���v �Ƃ����ϓ_�Řb��i�߂邱�Ƃɂ��܂��D
�����̓d���i�͂��鑤�̓d���j���~�N���ȃC���[�W�Ō���ƁC �P�P�̓d�ׂ��g���x v �h�œ����Ă��āC���ꂩ��g�� F �h���Ă��܂��D �͂��u�����v�́C�����̌��ʂ����̂܂��������ƁC ��̐}�̒ʂ�ɂȂ��Ă��邱�Ƃ��m�F�ł���Ǝv���܂��D �Ȃ��x�N�g���̌������o���o���ŁC���G�ł��D�D�D
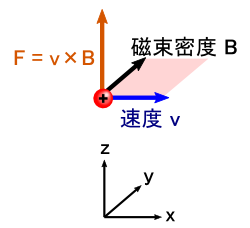
���̐}�́C�P�̓d�ׂ��u�d��v�Ɓu����v�̒��Ŏ��������ꂼ�ꎦ�������̂ł��D
�d��́C�d�ꎩ�̂̌����Ɨ͂��y�ڂ������������Ȃ̂ŁC�C���[�W���ȒP�������Ǝv���܂��D ����C�u����i�������x�j�v�̒��ł́C�g�d�ׂ����������h�Ɓg�������x�̌����h�Ɓg�͂̌����h�̂R���S�ĕʕ����Ńo���o���ł��D ���̂����ŏ��X��₱�����}�ɂȂ��Ă��܂��D

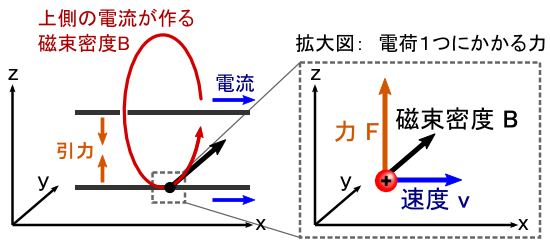
�������C�������x�̒��œ����d�ׂ���͂́C���ɃV���v���Ȏ��ŕ\���܂��D �Ƃ������C�P���ɂȂ�悤�Ɂu�������xB�v��s���悭���߂��Ƃ��������ł��D �̂̐l������Ɍ��߂܂����D ���̎�������C�u�d�� E �v�Ɓu�������x B �v���Ή��W�ɂ��邱�Ƃ�������܂��D
���āC��͂̑傫���͓d�� q �ɂ���Ⴗ��̂ŁC ���Ǘ� F �́C�gF = qvB�h�Ƃ������ŕ\����܂��D �����ʼn��߂ď�̎�������ƁC �������x B ���u��F�iN�j�v�Ɓu�d�C�ʂƑ��x�̐�qv�iC�Em/s�j�v�Ƃ��Ȃ����萔�Ƃ����������ł��܂��D �������x B �̒P�ʂ̓e�X���iT�j�ł������C���̒��g�� T =�iN�Es/(C�Em)�j���ƕ�����܂��D �iC/s�j= �A���y�A(A)�ł��邱�Ƃ��g���ĕό`����ƁC(T) =�i N/(A�Em) �j�ƂȂ�܂��D
�u�͂̑傫���v�̘b���ς̂ŁC���͗͂��u�����v�̘b�ɂ��ċl�߂Ă����܂��D ��������C�x�N�g���̊O�ς̘b���o�Ă��܂��D
���w�Z�⍂�Z�ł́u�t���~���O�̍���̖@���v�Ƃ������āC����̎w���g���Ċo�����肵�Ă��܂����D �������C���̂܂܂��Ɛ����̓y��ɏ悹�邱�Ƃ��ł��܂���D ������Ɓu�����d�ׂ����ꂩ���͂̌����v�Ƃ�������C ���w�I�Ɉ����i�܂�C�����ŕ\���j���������Ă��������Ƃ���ł��D
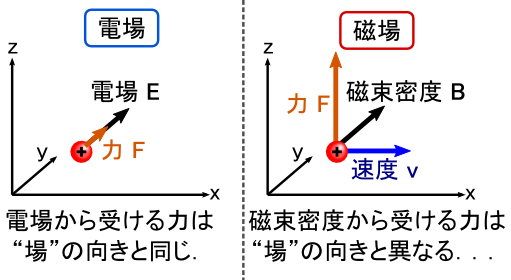
�d�ׂ���͂́C��̐}�̒ʂ�C�d�ׂ̑��x v �Ǝ������x B ��\���x�N�g��������ʂɑ��Đ����ł��D ��������W���ɏ悹��ƁC ���x v �������C�������xB�������̌����Ƃ���C��F�͂����̌����Ƃ��������ɂȂ��Ă܂��D ���̂��C���C���̈ʒu�W�i��}�F�E�j�͂R�������W�ň�ʓI�Ɏg���Ă�����̂ł����C������u�E��n�v�ƌĂԂ����ł��D �Ȃ��E��n�ƌĂ�邩�Ƃ����ƁC�E��̐e�w�C�l�����w�C���w�����ꂼ�ꂪ��������悤�ɊJ�����Ƃ��C �u�e�w�������C�l�����w�������C���w�������v�Ƃ������ԂɂȂ邩��ł��D ����ł͌����Ă����͂Ȃ�܂���D
����u�E��n�v���C���[�W���āC��F�́g�����h��\�����Ă݂܂��D
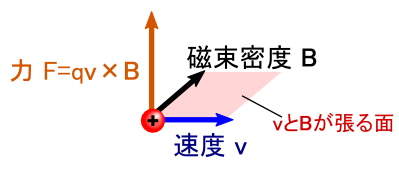
���́C�uv��B������ʂɐ����ȕ����Ƀx�N�g��F��L���v�Ƃ���������C �gF = v�~B�h�ƁC�����Z�̋L���g�~�h���g���ĕ\�����邻���ł��D �ꉞ�C���ꂪ���݂̃X�^���_�[�g�Ƃ������ƂŁC����������̊ԂŒ蒅���Ă���悤�ł��D
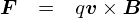
����͌��ǂ̂Ƃ���C���w�Z�ŏK���u���xv���玥�����xB�ɂނ����ĉE�l�W�����Ƃ��Ƀl�W���i�ތ����v�Ƃ������ɂȂ��Ă���킯�ł����D�D�D ���������C�u���̃C���[�W�𐔎��ŕ\�����Ƃ��ł����v�Ƃ����̂��d�v�ł��D �i�Ƃ͂����C�E�l�W�̃C���[�W�͒����I�ɂ킩��₷���̂ŁC��v�Z�����鎞�͂悭�g�����肵�܂��D�j
���́u�x�N�g���̊O�ρv�ɂ͌����Ƃ������C���Ԃ����܂��Ă��āC �gA�~B�h�ƁC�gB�~A�h�͕ʂ̃x�N�g���ɂȂ�܂��D �g�~�h�̋L���̑O�ɏ������x�N�g����x���C��ɏ������x�N�g������y���ɍ��킹�Ă�銴���Ȃ̂ŁC �O�ς̌��ʂł���x�N�g���iz���̌����j�͔��Ό����ɂȂ�܂��D �i�E�l�W�̃C���[�W�Ō����ƁC�l�W���������t�ɂȂ�܂��D�j
��̐}�̂悤�ɁC�gv�~B�h�ƁC�gB�~v�h�͕ʕ��ł��D �������x�����͂́C����gv�~B�h�̕��ł��Dv����ł��D �i����ς�C�uv����B�։E�l�W���v�Ɗo���Ă����̂�����ł͈�Ԗ𗧂��܂��D �Ƃ͂����C�����Łu�O�ρv�̕�����\���ł���悤�ɂȂ����̂͏d�v�ȓ_�ł��D�j
�������������C����̒��œ����d�ׂ���̘͂b�͑����܂��D�D�D
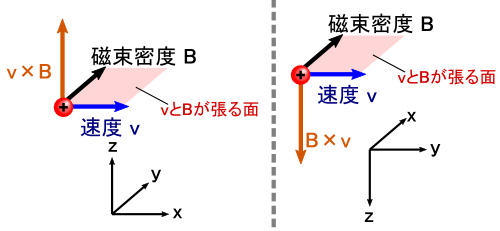
�����܂ł̘b�ł͏���ɁC��Ɂu�d�ׂ̑��xv�v�Ɓu�������xB�v�������ɂȂ��Ă��� �i�������Ă���j��Ԃ��l���Ă��܂����D ���̐}�̂悤�ɁCx,y,z�̍��W���̌����Ɗe�x�N�g���̌������Ή����Ă��鎖��������鎞�ɕ�����₷������ł��D
�������C���ۂɎ����Ȃ�����Ă��鎞�́C�u�d�ׂ̑��xv�v�Ɓu�������xB�v���������Ă���Ƃ͌���܂���D �i���ꂢ��90�x�̊p�x�ɂȂ��Ă���Ȃ�āC���������Ƃł��D ���͓d�ׂ����������ɑ債�āC����̌����̓e�L�g�[�Ȋp�x�ɂȂ��Ă��܂��D�D�D�j
�d�ׂ����ꂩ���͂̑傫���́C���xv�Ǝ������xB�̊Ԃ��p�x�ɂ���ĕω����܂��D
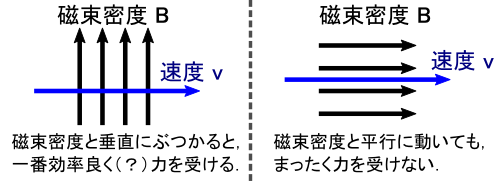
�d�ׂ̑��xv�Ǝ������x B ���g�����h�̎��́C ����܂ł̐����ʂ�C�d�ׂ͗��gF = v�~B�h���܂��D ����ɑ��āC�d�ׂ̑��x v �Ǝ������x B �����������C �܂��g���s�h�ɂȂ��Ă���ꍇ�́C �d�ׂ͑S���͂��܂���D �i�������x B ��\�����������C��ɐ����Ă���g�Łh�ɗႦ�āC �u�d�ׂ������Ď��������鎞�ɗ͂���v�Ɛ������ꂽ�肵�܂��D�j
�ł́C�u�d�ׂ̑��xv�v�Ɓu�������xB�v���g�i�i���h�ɂȂ��Ă���ꍇ���l���܂��D ���̏ꍇ�C �i�i�������̑��xv�̂����C���ۂɌ����Ă���̂��u�������xB�Ɛ����Ȑ��������v�ɂȂ�܂��D ����͒����I�ɂ�����₷���b���Ǝv���܂��D ����𐔎��ŕ\���ƁC���xv�Ǝ������xB�������p�x���g�Ɓh�Ƃ��āC���̐}�̒ʂ��uv�Esin�Ɓv�ƕ\���܂��D
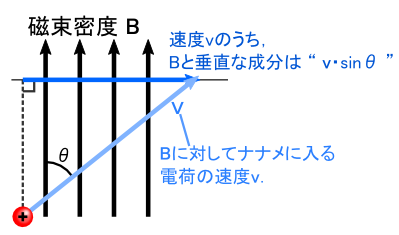
����ƁC�gv�~B�h�́u�傫���v���gv�EB�Esin�Ɓh�Ƃ����l�ɂȂ�܂� �i�u�����v�͂���B�ɉE�˂��������ɐi�ތ����ł��j�D
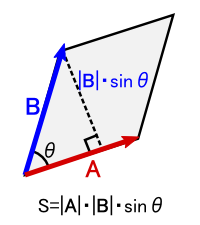
�����gvBsin�Ɓh�́C�}�`�I�ȃC���[�W�łƂ炦��ƕ�����₷���ł��D ���̐}�i���j�̂悤�ɁC�ӂ̒�����A�CB�ƂȂ��Ă��āC�Ԃ̊p�x���Ƃł��镽�s�l�ӌ`���v�������ׂ܂��D ����ƁC�gABsin�Ɓh�Ƃ����̂͂��傤�����̕��s�l�ӌ`�̖ʐ��ɂȂ��Ă��܂��D
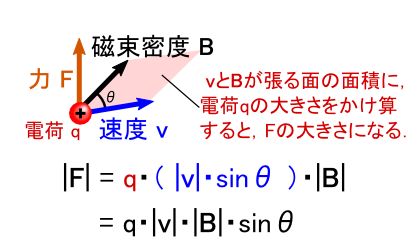
�����b���gv�h�ƁgB�h�ɂ��Ă���ƁC ��F�̑傫�����uv��B�����镽�s�l�ӌ`�̖ʐρv�ɁC�����Ă���d���̂̑傫��q�������Z�������́E�E�E �Ƃ������ƂɂȂ�܂��D �u�x�N�g���̊O�ρv�̓p�b�ƃC���[�W���ɂ�����������܂��C ���̒l�́u���s�l�ӌ`�̖ʐρv�Ƃ����}�`�I�ȃC���[�W�ő������܂��D ����ɁC�O�ς̌��ʐV�����o�Ă���x�N�g���̌����́C�u���s�l�ӌ`�ɐ����v�ł��D ����āC�Q�̃x�N�g���̊O�ς��l����Ƃ��́C ���̂Q�̃x�N�g���������u���s�l�ӌ`�v���̂��ƕ�����܂��D
�����ŁC����܂ł̘b�����܂Ƃ߂Ă����܂��D
�x�N�g���̊O�ς̘b�C�Ō�̂P�ł��D
�����܂ł́u�d�ׂ̑��xv�Ǝ������xB���Ȃ��p�x�Ɓv�Ƃ�������g���Đ}�`�I�ȃC���[�W�Řb��i�߂Ă��܂����D �������Cv �� B ���x�N�g���Ȃ̂ŁC�u�x�N�g���̐����v�����Ńx�N�g���O�ς̌v�Z��i�߂���͂��ł��D
���ہC�v�Ȃǂ�����ōs�����́C�R���s���[�^���g���Čv�Z�����܂��D ���̏ꍇ�C�}�`�I�ȃC���[�W��r�����ď����ɐ��l�����̉��Z�ŕ\�����Ȃ���Ȃ�܂���D �����������ꍇ�ɑΉ��������E�E�E�Ƃ����̂����`�x�[�V�����ɂȂ��Ă��܂��D �g�Ɓh�Ƃ����u�p�x�v�Ȃ�Ă��̂́C�u���s�l�ӌ`�v�Ƃ����}�`���C���[�W���ď��߂ďo�Ă�����̂Ȃ̂ŁC �}�`�̃C���[�W�����C�Ƃ��g�킸�Ƀx�N�g���̊O�ς�\���������킯�ł��D
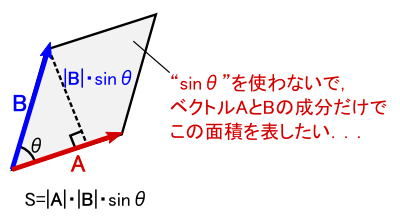
����Ȃ킯�ŁC���̐}�̂悤�� A (Ax�CAy) �� B (Bx�CBy,) �Ƃ����Q�̃x�N�g������镽�s�l�ӌ`�̖ʐς����߂邱�Ƃɂ��܂��D
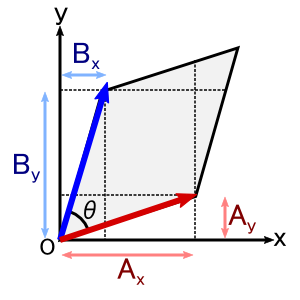
�ȒP�̂��߁C�x�N�g��A�CB����xy���ʏ�̃x�N�g���ɂ��Ă��܂��D ���̂Q�̃x�N�g���̊O�ς��Ƃ�ƁCz���i�}�ɂ͏����Ă��܂��j�Ɍ������āgA�~B�h�Ƃ����x�N�g���������銴���ɂȂ�܂��D
������ƃS�`���S�`�����Ă��܂��܂����C ���̐}�̂悤�ɂ����x�N�g��A��B�����镽�s�l�ӌ`�̕����̖ʐ����v�Z���Ă݂܂��D
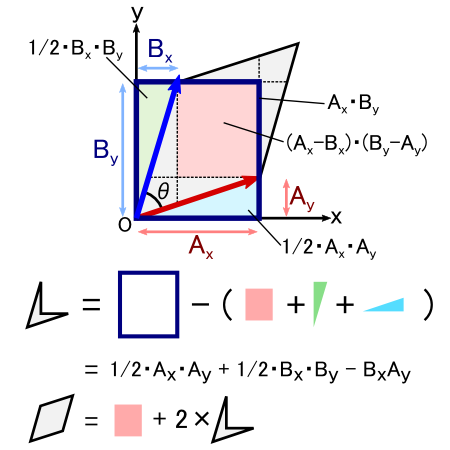
���ǁC���s�l�ӌ`�̖ʐς́u�g�s���N�̎l�p�h�{ 2�~�g�D�F�̕ςȌ`�h�v�ŁC���̎��ŋ��߂��邱�ƂɂȂ�܂��D
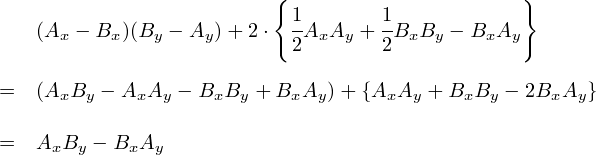
�ȏ�̌v�Z����C�gA�~B�h�̑傫���́C�gAxBy - AyBx�h�ŕ\����鎖��������܂����D ���ǂ��ł����C����́gA�~B�h�Ƃ����x�N�g�����uz�����v�ł� �iA��B��xy���ʏ�̃x�N�g���Ƃ����̂ŁC�O�ς�����z�����Ƀx�N�g�����L�тĂ����܂��j�D
���ŏ����ƁC�ȉ��̂悤�ɂȂ�܂��D
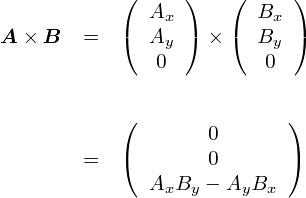
������Ƃ�₱���������ɂȂ��Ă��܂����C���̂悤�ȃC���[�W�Ŋo����Ɗy�i��������܂���j�D �uz�����v���l����ꍇ�́Cz�̎��ɂ���ux�v����Y�������X�^�[�g�����܂��D ����āC�P�ڂ̍��̓Y�����́gx��y�h�ŁC�gAxBy�h�ƂȂ�܂��D �Q�ڂ̍��̓Y�����́C�P�ڂ̍��̓Y�������t�ɂ��܂��D�܂�C�gy��x�h�ł��D ����āC�gAyBx�h�ł��D ���Ƃ́C�P�ڂ̍�����Q�ڂ̍��������Z���āC �gAxBy - AyBx�h �ƂȂ�܂��D �x�N�g���̊O�ς��v�Z���鎞�́C�����������D�D�D�Ə��Ԃɓ��̒��ł��邮������ɂȂ�܂��D
���C���C���̂R�������ׂĂ��v�Z����ƁC�ȉ��̂悤�ɂȂ�܂��D ���̎��̊e�������\���Ă���̂́C�u�P�Ȃ镽�s�l�ӌ`�̖ʐςȂv�ƍl����ƁC ������Ƃ͐e���݂₷���Ȃ邩���i�H�j����܂���D
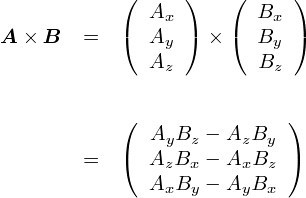
�ł́C���߂āC�d�ׂ̑��x���Ǝ������xB�̊O�ς��v�Z���Ă݂܂��D �P�ɁC�������ς���������ł��D
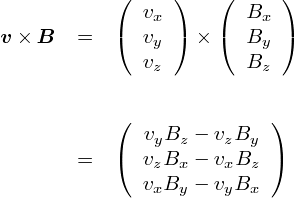
��̎�����C�d�ׂ����ꂩ�����gF = q�Ev�~B�h�͈ȉ��̂悤�ɂȂ�܂��D
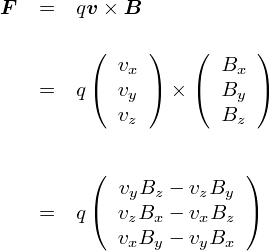
����ŁC�悤�₭�����Ă���d�ׂ����ꂩ�����𐔎��ŕ\�����邱�Ƃ��ł��܂����D ���Ƃ��Ă��gF = q�Ev�~B�h�Ƃ����Z�����̂ł����C ��������ς������̂ŁC�����܂ł���̂������Ȃ��Ă��܂��܂����E�E�E�D
�d�ׂɂ͂��炭�͂ɂ��Đ����ł����̂ŁC�悤�₭�C ��Ԏn�߂̎����ŏo�Ă����u�d���ɂ͂��炭�́v���l���܂��D
��̐}�̒ʂ�C�u�d���v�͂�������̓d�ׂ̏W�܂�Ȃ̂ŁC �P�����P�P�̓d�ׂ���͂����v�������ƂŁC �u�d���S�̂���́v�����߂邱�Ƃ��ł��܂��D ����ƁC�d��I���������xB�����͂́C�ȉ��̎��ƂȂ�܂��D
����ŁC�悤�₭�C�u�d�����������x�����́v�𐔎��ŕ\�����Ƃ��ł��܂����D �d���̒����il�j�������Ȃ�قǎ�͂��傫���Ȃ�Ƃ����̂́C ���ꂾ���d�ׂ̐��������邩��E�E�E�Ƃ������ƂŁC�����I�ɗ����ł��邩�Ǝv���܂��D�D�D
�����܂łŁC�d�����u��́v�̘b�͑S�ďI���ł��D
���́C�u�d�����������x B ������v�Ƃ����b�ł��D ���Ȃ��݁i�H�j�́C�u�r�I�E�T�o�[���̖@���v�Ƃ���������܂��D
�Ƃ肠�����C�����܂ł̓��e�ł́C�d�� I ���������x B ������ F �́C
�ŕ\����邱�Ƃ�������܂����D �����Œ��ӂ��Ăق����̂́C �u�������x B �v�Ƃ����̂́C�� F ��P���Ȏ��ŕ\����悤�Ɂi����Ɂj���߂��� ���Ƃ������Ƃł��D �P�̓d�ׂ��������x�����͂��u F = q�E�iv�~B�j �v�ƕ\�����ƂɌ��߂��̂��S�Ă̎n�܂�ł��D ����́C�d�ꂩ���͂��u F = q�EE�v�Ȃ̂ŁC ����Ǝ����`�ɂ���Ε�����₷�����낤�Ƃ��������Ō��߂��܂����D

�ł́C���́u�������x B �v�Ƃ�������C���������ǂ�����Ĕ�������̂��H�Ƃ��������C�ɂȂ�܂��D �O�ɂ����グ���C�u�d���̋߂��Ɏ���u���ƁC���܂����������w���v�Ƃ��������i��}�j����C �d�����������x������Ă���낤�Ɨ\�z�͂ł��܂��D �������C�u�ǂ̂��炢�̓d���𗬂��C�ǂ̂��炢�̑傫���i�����j�̎������xB���ł���́H�v �Ƃ������͑S���������Ă��܂���D���̕ӂ̓��e���C�����������o���Ă�����Ƌ��߂邱�Ƃɂ��܂��D
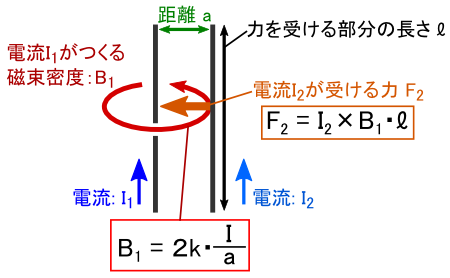
�O�� �u����v�Ƃ́H �̂Ƃ���Ŋm�F�����ʂ�C�Q�{�̕��s�d���̊Ԃɂ͗͂��͂��炫�܂��D �͂��͂��炭�����́C �u���ꂼ��̓d�����������x������C���̎������x�ɂ���Ă����Е��̓d�����͂��邩��v ���ƍl���Ă��܂����D

��͂�C�S�Ă̍��{�͏�}���u�d���ǂ����ɂ͂��炭�́v�Ȃ�ł��D ����āC�u����̑傫���v��l�Ƃ��Ă�����ƌ��肷��ɂ́C �d���ǂ����ɂ͂��炭�͂����Ƃɍl�����̂��ł��傤�D
����Ȃ킯�ŁC�̂̃G���C�Ȋw�҂̕��X�́C�Ƃɂ����u�d���ǂ����ɂ͂��炭�́v�̎������J��Ԃ��܂����D �ŏ��͂ƂĂ��P���Ȏ�������n�߂��悤�ł��D���̎菇�͈ȉ��̒ʂ�ł��D
��̎����̌��ʁC�d������͂́u�d���ʂ��傫���قNj����C���������傫���قǎア�v�Ƃ����������ʂ�����ꂽ�����ł��D �܂��C������O���낤�E�E�E�Ǝv���Ƃ���ł��D ������Ɛ��w���ۂ������C �u�d������͓͂d���ʂɔ�Ⴕ�C�����ɔ���Ⴗ��v �Ƃ��������ł��D
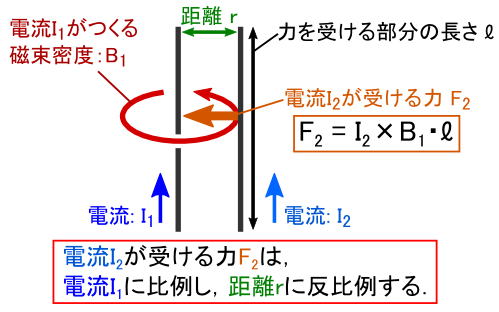
���ꂩ��C�u�d���P�v�͎������鑤�C�u�d���Q�v�͗͂��鑤�Ƃ��Č��Ă����܂��D �i������Ђ�����Ԃ��Ă��C�S�������c�_���ł��܂��D�j ���ǂ��ł����C�d���Q����� F2 ���u F2 = I2�~B1�El�v�Ƃ������ŕ\����̂ł����D �i�����ŁgB1�h�́u�d���P�ɂ���Đ������������x�v�ł��D�j
�d�� I2�̑傫����C�d�� I2�̒��� l ��ω������Ă��Ȃ��̂ɁC I2����� F2���ς��E�E�E �Ƃ������Ƃ́C�u�d���P����� �g�������x B1�h �̋������ς�邩�炾�v�ƍl����̂����R�ł��D ���Ȃ킿�C �d�� I1�����g�������x B1�h�́C �uI1�ɔ�Ⴕ�C���� r�ɔ���Ⴗ��v �Ƃ������ƂɂȂ�܂��D
���R�Ƃ����C���R�Ȍ��ʂł��D �u�d�����傫���قǔ������鎥��͋����āC�������痣���قǎ���͎�܂�v�Ȃ�āC ���������Ȃ��Ă������I�ɗ\�z�ł��錋�ʂ��Ǝv���܂��D�D�D ���������R���𐔎��ŕ\���ƁC�ȉ��̂悤�Ȋ����ɂȂ�܂��D
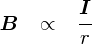
���āC���ܗ~�����̂́C�������xB���ǂ̂悤�ɂł���̂��H����������u�����v�ł��D �������C����o�Ă�����̎��́C���܂�ɂ��t���b�Ƃ��������ŁC �������x B �̒l��������ƒ�߂邱�Ƃ͂ł��܂���D
�{���ɗ~�����̂́C��̎��̂悤�ȁC�uB�̒l�����߂邱�Ƃ��ł�������v�ł��D ���Ȃ݂ɁC����̓d��o�[�W�������u�N�[�����̖@���v�ł��D �d��̕��͊��Ɂu�����v���������Ă��܂��D ����Ȃ�C�u�d��̃N�[�����̖@���Ǝ����悤�Ȋ����ŁC�������x�̖@�������Ȃ����ȁH�v �ƍl���Ă��܂��܂��D ����Ɠd��́C�Ȃ������đΏ̓I�ȃC���[�W������̂ŁC�����ƂȂ�Ƃ��Ȃ��Ȃ����Ǝv���Ƃ���ł��D
����Ȃ킯�ŁC�d��Ɋւ���u�N�[�����̖@���v���}�l���Ď������x B �Ɋւ���@�������炢���ȁE�E�E�Ƃ����C�����ŁC ���ꂩ��̘b��i�߂Ă����܂��D
���炽�߂āC �u�d������鎥��i�������xB�j�Ɋւ���@���v���l���邽�߂ɁC �����悤�ȏ�Ԃ́g�d��E�h���l���Ă݂܂��D �������x�����u�d���v�Ǝ����`�E�E�E�ƂȂ�ƁC �u�d�ׂ���ɔz�u�����_�v�Ȃ��`�Ƃ��Ă͎��Ă��܂��D �Ƃ肠�����C�u�Ȃג����������v���x�̍l���ł��D
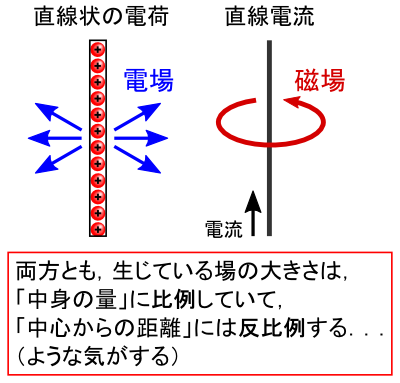
��}�̃C���[�W���ƁC�u������̓d�ׁv���C�u�����d���v���C�����Ă����̌`�͈Ⴂ�܂��D �������C�u��̋����i�傫���j�́C���g�̗ʂɔ�Ⴕ�ċ����ɔ���Ⴗ��v �Ƃ����_�͋��ʂ��Ă���C�����܂��D �������C�����I�Ɂu�Ȃ�ƂȂ��C�����v���v�����Ȃ̂ŁC�{���ɂ����Ȃ��Ă��邩�����������o���Ċm�F���Ă݂Ȃ��ƕ�����܂���D�D�D
����Ȃ킯�ŁC�u������̓d�ו��z�����g�d��E�h�v���ǂ̂悤�ɂȂ��Ă���̂��C �N�[�����̖@���������Ē��ׂĂ݂邱�Ƃɂ��܂��D
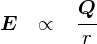
�㎮�̂悤�Ȍ��ʂɂȂ邱�Ƃ����҂���킯�ł��D ���Ȃ킿�C����u�d�חʂɔ�Ⴕ�C�����ɔ���Ⴗ��v�Ƃ�����ł��D
�ł́C�u�������̐��d�ׂ�����d��v���C�N�[�����̖@�����狁�߂邱�Ƃɂ��܂��D �ϕ��v�Z���o�Ă��܂����C�債�����Ƃ͂��܂���̂ŁD�D�D
�u�������v�Ƃ��Ă���̂́C�v�Z����Ε�����܂����C�Ώ̐��̂��邫�ꂢ�ȓd�ꂪ�ł��邩��ł��D �܂��C�u���d�ׁv�Ƃ������ƂŁC���Ȃ��݂��u�P�ʒ��������� �ρiC/m�j �̓d�ׂ�����v�Ƃ����ݒ�ɂ��܂��D �����������V�`���G�[�V�����œd������߂鎞�̏퓅��i�́C�����Ȓ��� dz ���Ƃ� �u�d�בf�ЁF�� �Edz�iC�j�v���������d���gdE�h������ƌ��邱�Ƃł��C ���� �gdE�h ��S�������Z�i�ϕ��j���Ă��C�_��d�בS�̂����̂P�_�ɂ���d������߂邱�Ƃ��ł��܂��D
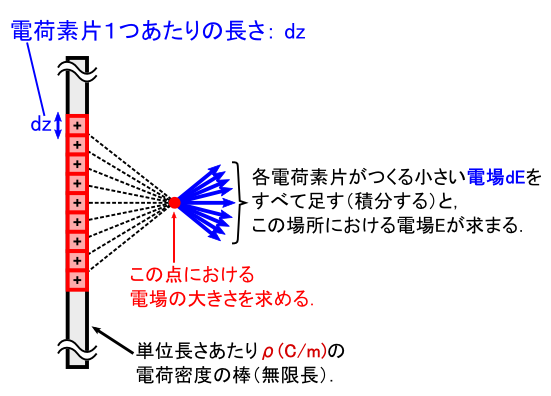
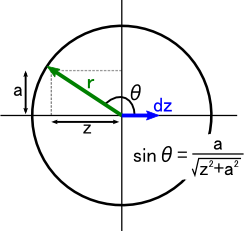
�ł́C�ȉ��̂悤�ɏc���i���������̃C���[�W�ŁCz���Ƃ��܂��j��p�ӂ��C ������W�gz�h�ɂ���d�ו��z���C���S���狗���gr�h�������ꂽ�ꏊ�ɂ���C �����ȓd��dE���N�[�����̖@�����狁�߂Ă݂܂��D
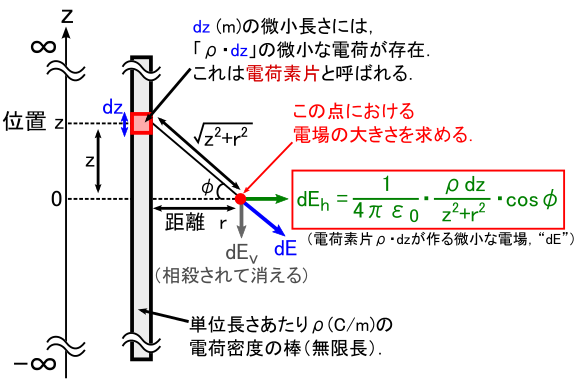
��̐}�̂悤�ɁC�ʒur�̏ꏊ�ɂł���d��� �u���������̓d��dEh (h��horizontal�̗�)�v�ƁC�u���������̓d��dEv (v��vertical�̗�)�v�ɕ����܂� �i�gd�h���t���Ă���̂́u�d�בf�Ђ���������ȓd��v�Ƃ����C���������߂Ă��܂��j�D ���̂����CdEv�͏�i�{���j���牺�i-���j�܂œd��𑫂����킹��ƁC���E���ă[���ɂȂ�܂��D ����Ȃ킯�ŁC�ʒur�ɂ�����d��E(r)�́C ����������dEh�݂̂�z=-������z=���܂ł̑S�͈͂ő������킹�����̂��E�E�E�Ƃ������ƂɂȂ�܂��D
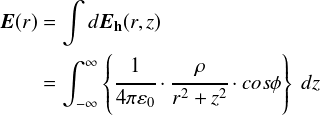
�����ŁC�usin�Ӂv�̓ӂƂ����ϐ����܂�ł��Ďז��Ȃ̂ŁC �ϕ��ϐ�z���܂`�ɕό`�������Ƃ���ł��D ��̐}����C
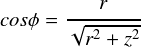
�E�E�E�ƂȂ�܂��D����������āC
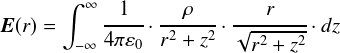
�����ŁC���Ȃ��݂̒u���ϕ��ł����C�uz = r�Etan�Ɓv�ƒu�������Ă��܂��D �i�����Ŏg�p����Ƃ́C����łĂ����p�x�́u�Ӂv�Ƃ͊W����܂���D�j
�܂��C�ψ�̊m�F�ł��D
| z | -�� �� �� |
| �� | -��/2 �� ��/2 |
���ɁC�u���ݕ��v��dz�̕�����u�������܂��Dz = r�Etan�Ƃƒu�����̂ŁCdz/d�Ƃ͎��̂悤�ɂȂ�܂��D
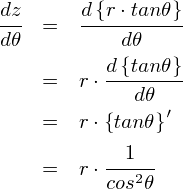
���Ƃ́CE(r)�Ɋւ���ϕ��v�Z����C�ɂ��܂��D
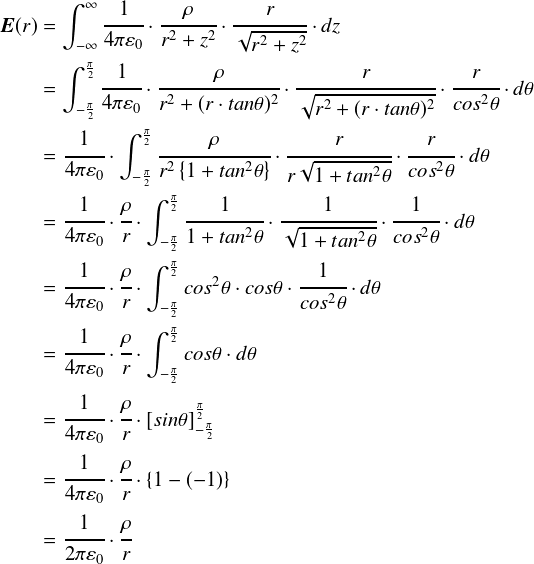
���ǁC�u�������̓d�ו��z������d��v�́C���̂悤�Ȏ��ɂȂ�܂����D
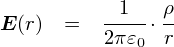
�u1/2��0�v�̕����͒萔�ł��D ��������u�d��̋����̓ςɔ�Ⴕ�Cr�ɔ���Ⴗ��v�Ƃ������ʂɂȂ��Ă��܂��D ����́C�~�����������_�ƈ�v���Ă��܂��D �Ƃ肠�����C�Ђƈ��S�ł��D
�����ŁC����̘b�ƂȂ��邽�߂ɁC�����܂ł̗�������Ă����܂��D
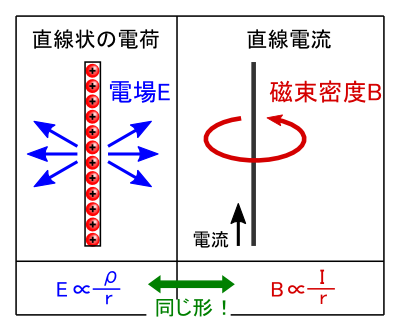
�S�`���S�`���Ɛϕ��v�Z�������������ŁC�u�������̓d�ו��z�����d��́gE ���/r�g �̌`�v�Ƃ������Ƃ�������܂����D ����ɑ��āC�������x�̕����u�������̒����d�������鎥�����x B �� �gB �� I/r�g �̌`�v�ƂȂ��Ă��܂��D
����̘b�͂����̎������ʂŁC�������́w�@���x�Ƃ����̂͂܂��������Ă��܂���D �Ƃ͂����C�d��Ǝ������x���ׂ�Ǝ��̌`���ƂĂ��悭���Ă���̂ŁC �u�����ƁC�������̖@���������悤�Ȏ��̌`�Ȃ�Ȃ����H�v�Ɗ��҂ł��܂��D
����ł́C���������q���g�������Ă����̂ŁC �{����u�d�����������x�����@���v��g�ݗ��Ă邱�Ƃɂ��܂��C �������C�d��Ɣ�r���Ȃ���C���Ă���_���z�����Ă��������Ői�߂܂��D �����ŁC���̕\���C�g�P�ʁh�ɒ��ڂ��Č��Ă��������D

�܂��͓d��ł��D�u�����d�ׂ����d��̎��v�ł��g�d�ז��x�ρiC/m�j�h�Ƃ����ʂ��o�ꂵ�Ă��܂����D ����ɑ��āC�d��̍������̖@���Ƃ�������u�N�[�����̖@���v�ł́C�g�d�C��Q�iC�j�h�����ɏo�Ă��܂��D ���̓d�C��Q�́C���R�Ȃ���C�u�d��������{�I�ȗʁv�ł��D �����āC���̓d�C��Q�Ɠd�ז��x�ς̊W�́C�u Q (C) = ��(C/m)�~l (m) �v�Ƃ�����ɁC �ς��u���� l (m) �v�������Z������ �ƂȂ��Ă��܂��D
���Ɏ������x�ł��D�������̓d�����������x����鎮�ɂ��g�d�� I (A)�h�Ƃ����ʂ��o�ꂵ�Ă��܂��D ��Ŋm�F�����d��̘b����ސ����āC�u���� l (m)�v�������Z����u�������{�I�ȗʁv������̂ł́H �Ɓi���̏�̐����Łj�l���Ă݂܂��D ����ƁC�gI�El (A�Em)�h�Ƃ������̂��o�Ă��܂��D ���́gI�El (A�Em)�h�̒P�ʂ�����������ƁCI�El (C�Em/s)�ƂȂ�܂��D �iA = C/s �Ȃ̂ŁD�j ���� C�Em/s �Ƃ����P�ʁi�����j�́C�u����v(m/s)�œ����d�C��(C)�v��\���Ă��邱�Ƃɑ��Ȃ�܂���D �������x�̕����ł��Ȃ��݂��gqv�h�Ƃ�����ł��D�ӊO�ƁC�Ӗ��̂���ʂ��o�Ă��܂����D
���āC���́u���� l�v�Ƃ��������ɒZ�����āC�g�����Ȓ��� dl �h�ɂ���ƁC ���̐}�̒ʂ�C�u����P�_�v�ɂ�����d�ׂ�d����\�������ɂȂ�܂��D ���́g�^���I�ȓ_�d�ׁh���u�d�בf�Ёv�ƌĂ�Ă��āC ���l�ɁC�g�^���I�ȓ_�d���h���u�d���f�Ёv�ƌĂ�Ă��܂��D �i�g�����Ȓ����h�Ƃ������o���Ă���̂ŁC�����E�ϕ��̃Z���X���܂܂�Ă��銴���ł��D�D�D�j
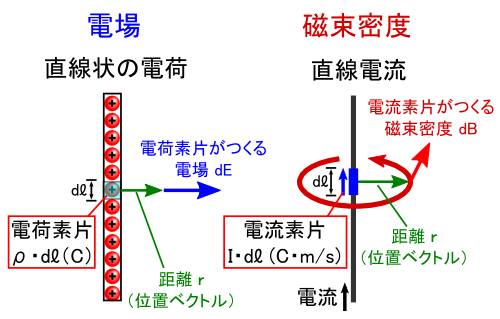
�d�� E �̏ꍇ�͓d�בf�Ёg�ρEdz�h�������ȓd��gdE�h������̂Ɠ����悤�ɁC �������x B �̏ꍇ���u�d���f�ЁgI�Edl�h�������Ȏ������x dB ������v�ƍl���邱�Ƃ��ł������ł��D ���̃C���[�W���ɂ��C �u�d���ɂ���Ĕ������鎥�����x�̎��v�����������Ă݂܂��D
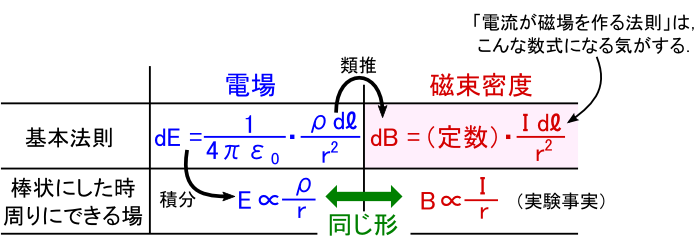
��̕\�ł́C�N�[�����̖@���ɂ����� �g�� dl�h �̕������C�P���� �gI dl�h �ɒu�������āu�������x�̊�{�@���v������Ă��܂��D �������Ăł������������̎����C �u�r�I�E�T�o�[���̖@���v (Biot-Savart law) �Ƃ�����ł��D
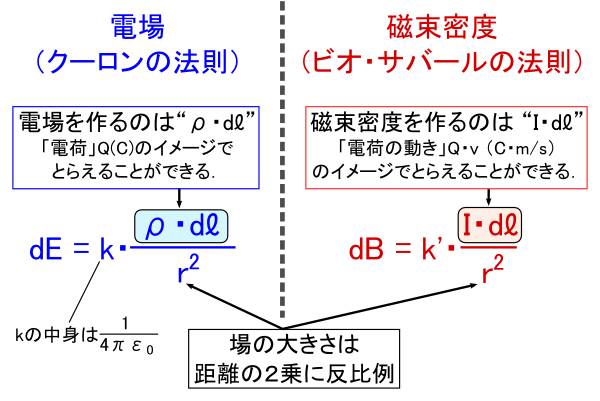
���ǁC�d��Ǝ������x�́C���ꂼ��u�d�ׁv�Ɓu�d�ׂ̓����v���g��h������Ă��邱�ƂɂȂ�܂��D �����āC�d�ׂ�����ʒu���痣���قǁC�����̂Q��ɔ�Ⴕ�ď�̑傫���͎�܂�܂��D �d�ׂ̑傫����d���̑傫���ƁC���ۂɂł���g��h�̑傫���Ƃ̒��K�����킹�邽�߂ɁC �uk�v��uk�f�v�Ƃ����萔���g���Ă���킯�ł��D
��̎��ł́C�萔���uk�v�C�uk�f�v�ƕʁX�ɐݒ肵�Ă��܂��D �d��Ǝ������x�̑傫���̓o���o���Ȃ̂ŁC���R�ł����E�E�E�D �����ŁC �u���Ⴀ��̓I��k'�̒l�͂����Ȃ́H�v�Ƃ������Ƃ��C�ɂȂ�܂����C����͌�X���߂邱�Ƃɂ��܂��D �Ƃ肠�������́C�u�d�����������x�����@���v�̎��̌`�����������Ƃ������ƂłЂƒi���ł��D
�u�r�I�E�T�o�[���̖@���v�̘b�ł́C�܂��u�������鎥��̌����v�ɂ��āC �����ŕ\����Ƃ��c���Ă��܂��D ���ꂩ��l�߂Ă����܂��D

��̐}���C�e�x�N�g�����u�����v�ɒ��ڂ��Č��Ă��������D�u�d���f�Ђ̌����i�x�N�g���gdl�h�j�v�C �u��������߂����ꏊ���w���ʒu�x�N�g���i�x�N�g���gr�h�j�v�C �u�d���f�Ђ���鎥�����x�i�x�N�g���gdB�h�j�v �́g�����h�̊W�́C���傤�Ɖ��̐}�̒ʂ�C�gdB = dl�~r�h�̊W�ɂȂ��Ă��܂��D �i dl ��x�������C r ��y�������C dB ��z�������E�E�E�Ƃ�����ł��D �����ƌ����C dl ���� r �։E�l�W���āC �l�W���i�ތ����� dB ���L�т܂��D �j
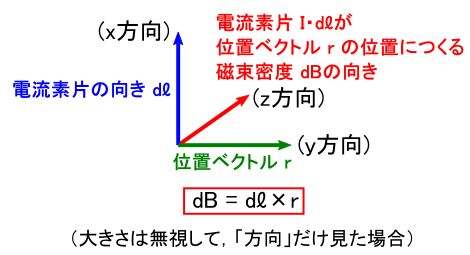
�������C�u�����v�̘b���������Ă���̂ŁC �x�N�g���̒����i��Βl�j�́udB = dl�~r�v�̒ʂ�ɂȂ��Ă͂��܂���D�D�D
�Ƃ肠�����C�������鎥�����xB�̌����́C�u�d���̌��� dl �� �ʒu�x�N�g�� r�̊O�ς��Ƃ��������v�ƂȂ��Ă��܂��D ���āC����̘b�̍ŏ��̕��ŁC �����d�������鎥��́u�d���𒆐S�Ƃ����Q�v�ɂȂ��Ă��邱�Ƃ��m�F���܂����D ���́u�O�ρF �gdl �~ r�h�v���g�����l�����ŁC������Ǝ�������������ł��邩�m�F���Ă݂܂��D

�^�̓d���i�������gdl�h�j����C����̊e�_�ֈʒu�x�N�g���gr�h��L���C �gdl�~r�h�̌������P�_�����߂Ă����܂��D �i���ǂ���������܂��C�������x�gdB�h�́C�ʒu�x�N�g���Ŏw�����ꏊ�ɂ�����l�Ȃ̂ŁC �x�N�g���gr�h�̐�[���n�_�ɂȂ�悤�ɊG��`���Ă����܂��D�j
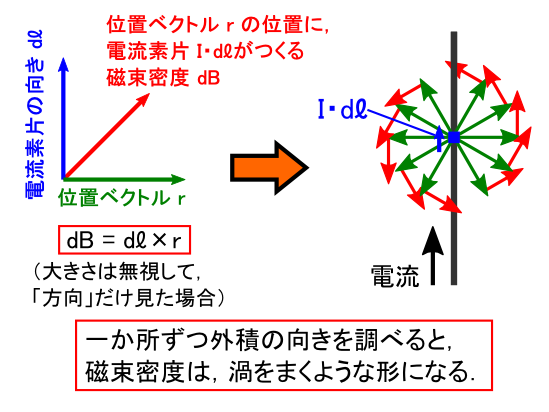
������ƁC�d���̎���ɂł��鎥�����x���l����ƁC������ƉQ��ɂȂ��Ă��邱�Ƃ��m�F�ł��܂����D �i���ۂɁu�E�l�W�v�̒��ʼnāC�m�F���Ă݂Ă��������D�j ���ɖ��Ȃ������Ȋ����ł��D �ȏ�̓��e���C�u�r�I�E�T�o�[���̖@���v�̎��ɐ��荞�ނƁC���̂悤�Ȋ����ɂȂ�܂��D
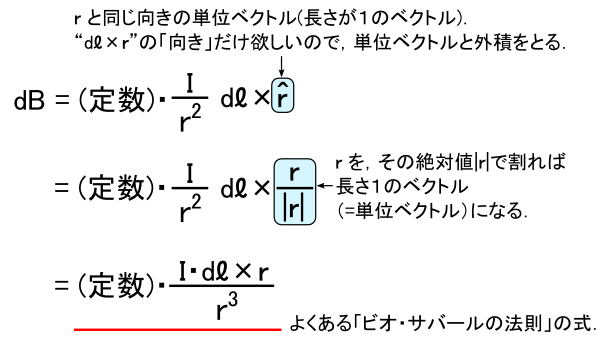
�����܂ł̘b�ŁC�udl�~r�v�̌����������~�����D�D�D�Ƃ����C�����ɂȂ��Ă��܂����D �������xdB�́u�l�i= �x�N�g���̐�Βl�j�v�Ɋւ��ẮC �������g�i�萔�j�EI�Edl/r2�h�̕����ŕ\���ł��Ă��܂��D �������u�����v�̏��������邽�߂ɁC�P�ʃx�N�g���ƊO�ς��Ƃ��Ă��܂��D �P�ʃx�N�g���ƊO�ς��Ƃ����ꍇ�C�����͕ς��܂����C��Βl���̂��͕̂ς��܂���D
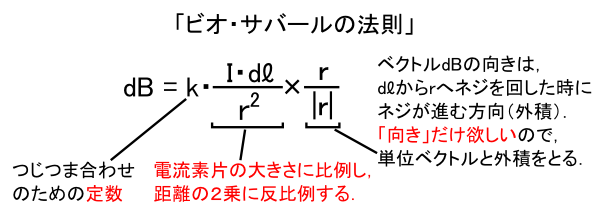
�ȏ�ŁC�u�r�I�E�T�o�[���̖@���v�̑�܂��ȕ����͌���ł��܂����D �r�I�E�T�o�[���̖@���̊e�p�[�c�i�H�j�́C��}�̂悤�ȃC���[�W�ő����邱�Ƃ��ł��܂��D �u�萔 k �̒l�v�̘b�́C���ɏd�v�ȓ��e�ł����C����������ŁD�D�D
�����܂ł̘b�ŁC�悤�₭�u�d������鎥��Ɋւ���@���v�C ���Ȃ킿�u�r�I�E�T�o�[���̖@���v�̌`���ł܂��Ă��܂����D �����{���ɂ��̎����������̂ł���C��ԍŏ��̘b��ł�����������C �u�����d������鎥��́C�d���ʂɔ�Ⴕ�C�����ɔ���Ⴗ��v �Ƃ������Ƃ������g���ē�����͂��ł��D������Ɗm�F���Ă݂܂��D �i�܂��ϕ��v�Z�����܂��D�j
��̂��Ƃ��C�u�������̓d���v��z�肵�C���̊e�_�ɂ�����u�d���f�Ёv�����鏬�����������x dB ��S���������킹��i�ϕ�����j�E�E�E �Ƃ�������ł����܂��D�i�������̓d�ו��z�̎��ƁC�b�̗��͑S�������ł��D�j
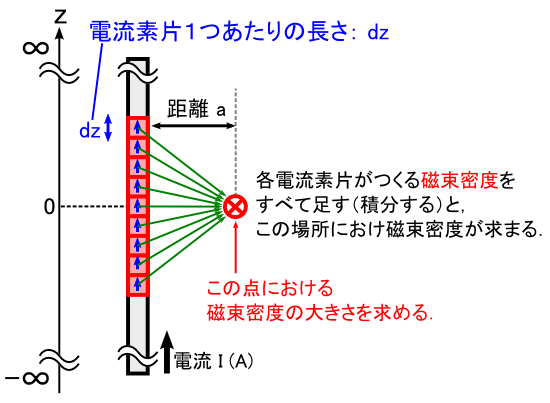
�d�������u���� a�v �������ꂽ�ꏊ�ɐ����鎥������߂�C�Ƃ����ݒ�ɂ��܂��D �i�d������鎥��́C�d�����g�𒆐S�Ƃ����~�i�Q�j�̌`�ɂȂ�܂��D ����̃P�[�X�ł́C�ga�h�́C���̔��a�Ƃ������ƂɂȂ�܂��D�{���́C�u���a�v���ۂ��gr�h���g�������Ƃ���ł����C �gr�h�͈ʒu�x�N�g���gr�h�Ƃ��Ă����g���Ă���̂ŁC�d���Ȃ��ga�h�Ƃ��܂����D�j
�K���ȏꏊ�ɂ���C�P�̓d���f�Ђ���鎥�����x�ɒ��ڂ���ƁC�ȉ��̂悤�Ȋ����ɂȂ��Ă��܂��D
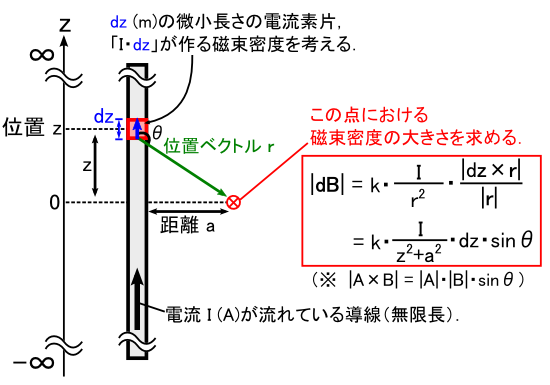
��̐}�̐Ԙg�̒��ł́C�r�I�E�T�o�[���̖@�����g���Ă��܂��D �O�ς̌v�Z�̕����ł����C���̕����͒P�Ɂu�d���f�Ђƈʒu�x�N�g���������p�Ɓv�����o�����߂ɂ���܂��D �i�P�Ɂu�����v��^���邾���̖ړI�ŁC�O�ς̕�����t���������̂ł����E�E�E�D�j
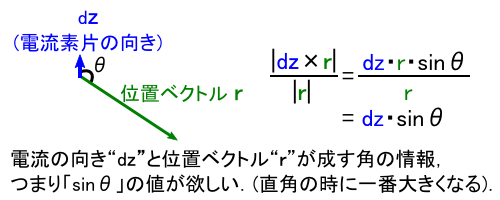
����킯�ŁC���ꂩ��u�������x�̑傫���v�����߂邽�߂̌v�Z���́C���̂悤�ɂȂ�܂��D
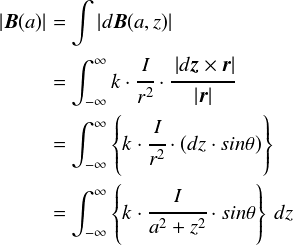
����̐ϕ��̐ϕ��ϐ��́C�gdz�h�ƂȂ��Ă��܂��D �����ŁC�p�g�Ɓh��z�ɂ���ĕω�����ʂł��D ����āC�ȉ��̐}�̂悤�ɍl���āC�Ƃ� z �̎��ŕ\���悤�ɂ��Ă����܂��D
����ŁC���ʂɁi�H�j z�Ɋւ��Đϕ����邾���̎����o���オ��܂����D
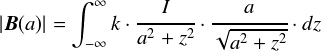
�����ŁC���Ȃ��݂̒u���ϕ��ł����C�uz = a�Etan�Ӂv�ƒu�������Ă��܂��D �i�����Ŏg�p����ӂ́C����łĂ����p�x�́u�Ɓv�Ƃ͊W����܂���D�j
�܂��C�ψ�̊m�F�ł��D
| z | -�� �� �� |
| �� | -��/2 �� ��/2 |
���ɁC�u���ݕ��v��dz�̕�����u�������܂��Dz = a�Etan�ӂƒu�����̂ŁCdz�́C
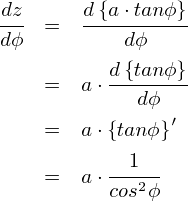
�E�E�E�ƂȂ�܂��D����ł́C z �Ɋւ���ϕ����ӂɊւ���ϕ��ɒu�������āC �Ō�܂Ōv�Z���Ă����܂��D
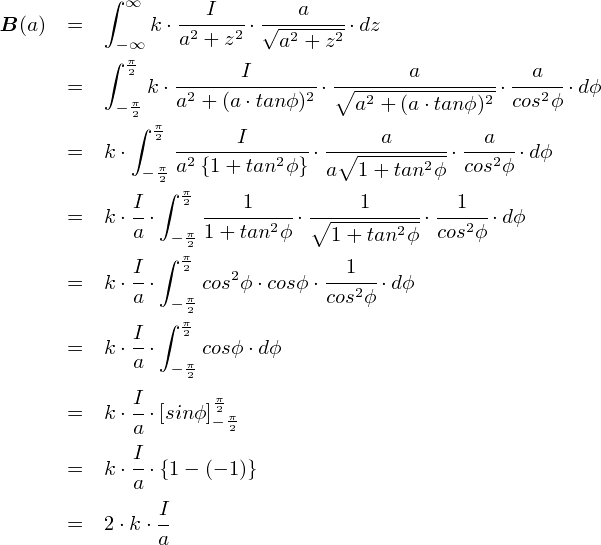
����Ȃ���ȂŁC�u�������̒����d�������鎥�����x�v �́C�ȉ��̂悤�Ȏ��ɂȂ�܂����D
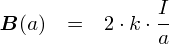
����́C�u�d�������鎥�����x�́C�d���ʂɔ�Ⴕ�āC�����ɔ���Ⴗ��v �Ƃ��������������̂��̂ł��D ����āC����܂ō���Ă����u�r�I�E�T�o�[���̖@���v�͑Ó����ƍl���ėǂ������ł��D
���Ă��āC���͂悤�₭�u�萔 k�v�̒��g�Ɋւ��b�ł��D
�����܂ł̘b�ŁC�u�d�����������x�����́v�̎��ƁC �u�d�������鎥�����x�v�̎��̗����������܂����D �����܂ŏo�Ă�����������ʂ肨���炢���Ă����܂��D
�܂��́C�u�����d�ׂ����ꂩ���́v�̎��ł��D
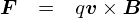
��̎����g���āC�u�d�����i�P�ʒ���������j��́v���ƁC�����̂悤�ɂȂ�܂��D
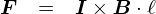
���x�͋t�ɁC�d�����������x�������Ƃ����b�ł��D ����́C�������u�r�I�E�T�o�[���̖@���v�ɂ܂Ƃ߂�ꂽ�̂ł����D
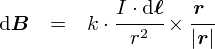
��́u�r�I�E�T�o�[���̖@���v���g���āC �u�������̓d�����狗�� a �̈ʒu�ɐ����鎥�����x�v ���v�Z����ƁC���̂悤�ɂȂ�܂��D
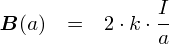
�ȏ�C�����܂Œ��X�ƍl���Ă������e�̌��_�������܂Ƃ߂܂����D �������炪�{��ł��D�D�D
��ԍŏ��ɘb��ɂ��Ă����C �u���s�d���̊Ԃɂ͂��炭�g�́h�Ƃ́C�ǂꂭ�炢�̑傫���Ȃ́H�v �Ƃ����b��ЂÂ��܂��D ���������̃��`�x�[�V�����́C�������痈���̂ł����D
���Ɋm�F�����ʂ�C�d������͂��uF = I�~B�El�v �ŋ��߂���̂ł����D���̎����g���ƁC��̐}�œd�� I2 ����͈͂ȉ��̎��ŕ\����܂��D
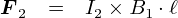
�������x B1 �̒l�ł����C�������̓d�� I1�����鎥�����x�̑傫���͈ȉ��̒ʂ�ƂȂ�܂��D ����́C�O�ɐϕ��v�Z�����ċ��߂Ă������̂ł��D
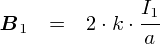
����āCB1 ��������ƁC�d�� I2����͂̑傫���͎��̂悤�Ȋ����ɂȂ�܂��D
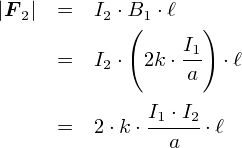
�����ŁC�b��P���ɂ��邽�߂ɁC�u�d���Ԃ̋��� a = 1m�v�C �u�͂���d���̒��� l = 1m�v�Ƃ��āC���ɑ�����Ă��܂��܂��D
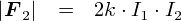
���āC�����ɂ����g�萔 k�h�̖������͂����蕪�����Ă��܂����D �萔 k �́C�u�d���ʂƗ͂̑傫���̋��n��������W���v���ƌ��邱�Ƃ��ł��܂��D �܂��C�萔 k �̒P�ʂ� �iN/A2�j ���ƕ�����܂��D
�����܂œ�����O�̂悤�ɁC�u�d���̒P�ʂ̓A���y�A (A) ���v�ƌ����Ă��܂������C ���́C�g1 �A���y�A�h�Ƃ����ʂ͂��̎������ɂȂ��Ă��܂��D
�������̎��ɁC I1 = I2 = 1 �������Ă݂�ƁD�D�D
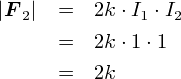
�㎮�̒ʂ�C�d�� I2 ����� F2 ���g2k�h (N) �ɂȂ�܂����D �Ȃ�C�P�����uk = 1 (N/A2)�v�Ɓi����Ɂj���߂Ă��܂����Ƃɂ��܂��D ����ƁC �u�P�A���y�A�̓d���Ƃ����̂́C���s�d���Ɍ݂��� 2 (N) �̗͂��͂��炭���̓d���ʂł��v �Ƃ����������Łu�P�A���y�A�v���`���邱�Ƃ��ł��܂��D
���ǂ��ł����C�����܂ł̘b�̗����}�ɂ܂Ƃ߂Ă݂܂��D

�萔 k �́C�d���̑傫���ƁC�����ɂ͂��炭�͂̑傫���̒��K�����킹�邽�߂̒l�ł��D ���Ȃ݂ɁC�����u�d���̑傫���Ɨ͂̑傫�������ԌW�� k �v�̂��Ƃ��C �u�������v (magnetic permeability)�ƌĂԂ����ł��D �������͕������ƂɈقȂ�܂����C�C���[�W�Ƃ��ẮC�u�ǂꂾ�����͂��͂��₷�����v�Ƃ������p�����[�^�ł��D �ǂ̒��x�g���ꂪ�����邩�H�h�Ƃ����������Łu�������v�Ƃ������{���ɂȂ����C�����܂��D�D�D
�����ŁC�u�P�A���y�A�v�Ƃ����ʂ��ǂ����߂邩�͐l�Ԃ̏���ł��D ����āC���̒萔 k �i�������j �Ƃ�����́C�A���y�A�̒�`�ɏ]���Ă���l�ɒ�܂邱�ƂɂȂ�܂��D ������ɂ��邩�H�Ƃ������Ǝ���ŁC�ǂ��Ƃł����߂邱�Ƃ��ł��܂��D
�����C���� k = 1 (N/A2) ���̗p�����C �O�ɏo�Ă����u�r�I�E�T�o�[���̖@���v�͌W���������Ȃ��āC�i������Ƃ����j�ȒP�Ȏ��ɂȂ�܂��D
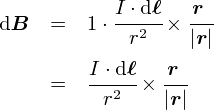
�������Ȃ���C���ۂ̂Ƃ���́Ck = 1 (N/A2) �ł͂���܂���D ����͗��j�I�ȗ��ꂪ���݂܂��D�D�D
�̂ނ����C�܂��g�d���ʂ̒P�ʁh�����܂��Ă��Ȃ��������C���Ɠ����b�������o���ꂽ�����ł��D �u�P�A���y�A�v�Ƃ����ʂ����܂��Ă��Ȃ������̂ŁC ���R�ł����C�d���ʂ����肷��ڈ����u���s�d���ɂ͂��炭�́v��������܂���D ���Ȃ�C
�E�E�E�Ƃ���C�萔 k�̒l��k = 1 (N/A2)�ƂȂ�C ���ɃX�b�L�����܂��D ���ǂ��ł����D���́g�萔 k�h�Ƃ����̂́u�r�I�E�T�o�[���̖@���v�̌W���ł����D ���̌W�����gk = 1�h�ł���Ȃ�C�r�I�E�T�o�[���̖@���̌W���͖����Ȃ�i1 �Ȃ̂Łj���ƂɂȂ�܂��D
�u�P�A���y�A�v�Ƃ����ʂ����肵�������C�G���C�Ȋw�҂����́C��͂蓯���悤�Ȏ����l���Ă��������ł��D �Ƃ��낪�C���ۂɌ���̓d���C�w�̋��ȏ������Ă݂�ƁC �r�I�E�T�o�[���̖@���̌W���ł��� k �̒l�́C �uk = 1�~10-7�iN/A2�j�v �Ə�����Ă��܂��D�P�^���S�R�Ⴂ�܂��D�D�D
���̌����́C���j�̗�������������Ă���Ƃ���ɂ���܂��D
���݁C��ʓI�ɗp������P�ʌn���uSI�P�ʌn�v�Ƃ�����ł��D ����ɑ��āC�͓̂d���C�w�̘b������ۂ� �uCGS�P�ʌn�v �Ƃ�������g���̂����s���Ă����i�H�j�炵���ł��D
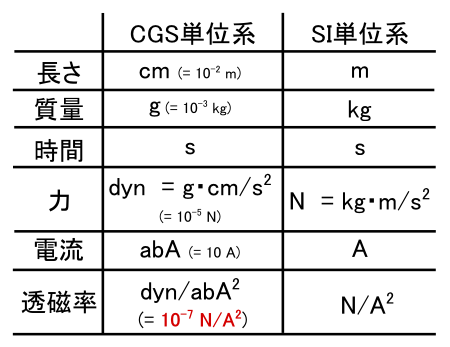
CGS�P�ʌn�ł́C�͂̒P�ʂƂ��āudyn �i�_�C���j�v�C �d���̒P�ʂƂ��āuabA �i�A�u�A���y�A�j�v ���g���Ă��������ł��D 1 dyn �� 1�~10-5 N �ɑ������܂��D �܂��C1 abA �� 10 A �ɑ������܂��D �����́C�u�͂Ƃ����C�P�ʂ� dyn �D�d���Ƃ����C�P�ʂ� abA ���D�v �Ƃ����̂��펯�ł�����C ����̎���ł���g�萔 k �h�̋c�_�ɂȂ������ɍl�������P�ʂ��gdyn�h�� abA �ł����D
����Ȃ킯�ŁC
�Ƃ�����ɁCCGS�P�ʌn�ɓs���̗ǂ��悤�ɓd���g�A�u�A���y�A�h�̒l���`���Ă��܂��������ł��D ���̏ꍇ�C�萔 k�̒l�́uk = 1 (dyn/abA2)�v�ƂȂ��āC�m����CGS�P�ʌn���g�����ꍇ�͎����������肵�܂��D
�������Ȃ���C���ݎ�Ɏg���Ă���P�ʌn�́uSI�P�ʌn�v�ł��D ����āC������ k = 1 (dyn/abA2) ���C���݂́u�A���y�A�v�Ɓu�j���[�g���v�ŕ\���ƁC k = 1�~10-7 (N/A) �Ƃ������ɂȂ����E�E�E�Ƃ����b�ł��D
�u�P�A���y�A�v�Ƃ����d���̒�`���C�����ɏ��������ƁC�ȉ��̂悤�ɂȂ�܂��D
�E�E�E����ł́C���炽�߂ăr�I�E�T�o�[���̖@���������Ă݂܂��D
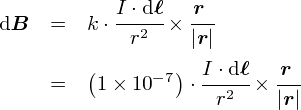
������ƒ萔 k �̒l���s���R�i�H�j��������܂��C �ȏ�ŁC�u�r�I�E�T�o�[���̖@���v���{���Ɋ����������ƂɂȂ�܂��D
���Ă��āC�悤�₭�g�܂Ƃ߁h�� �u�A���y�[���̖@���v �܂ŗ��܂����D
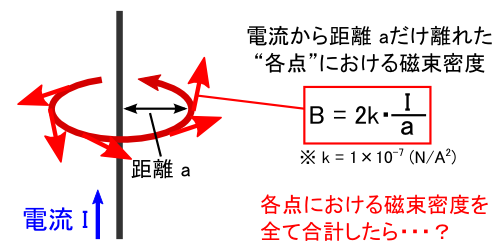
��̐}�̒ʂ�C�����d�������̎���ɔ��������鎥�����x�� B = 2k�EI/a �ƂȂ�܂��D ����̓r�I�E�T�o�[���̖@�����瓱�������̂ł����D �������Ȃ���C���̎��́u�����d���̎���́g�P�_�h�����v�̎������x�����\���Ă��܂���D �u�����d������鎥�����x�́C�g�[�^���łǂ̂��炢�Ȃ́H�v�Ƃ��������l���Ȃ��ƁC �{���̈Ӗ����u�d�� I �����������鎥�����x�͂��̂��炢���v�Ƃ������Ƃ�\�����C���ɂȂ�܂���D
����Ȃ킯�ŁC�����d�������������鎥�����x��S�������Z���č��v���邱�Ƃɂ��܂��D ���̎��́C�u�����d�����狗�� a �������ꂽ�ꏊ�ɐ����鎥�����x B�v��\���Ă��܂����C ���̎������x�͓d���𒆐S�Ƃ������a a �̉~��ŁC�ǂ��ł������l�Ƃ������ƂɂȂ�܂��D
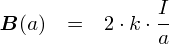
����Ȃ�C�u���a a �̉~�ɉ����Ď������x B �̒l�����v����v���ƂŁC �u�d�������� a �̏ꏊ�ɔ����������������x�v��S���\�����Ƃ��ł������ł��D �v�́C�~���̒��� 2��a �������Z���邾���ł��D�D�D
��̎��ł́C�u���ϕ��v�Ƃ�����ō���̌v�Z��\���Ă��܂��D �P���ɁC������[�v�ɉ����Ă�����Ɗe�ꏊ�̎������x�̒l�𑫂��Z���Ă��������ł��D ���Ȃ݂ɁC�e�ꏊ���Ƃ́u���[�v�ɉ����������v���l���Ă��ƁC ���̐}�̂悤�ɏꏊ�ɂ���ăo���o���ł��D ����Ȃ킯�ŁC�ϕ����鎞�͂��́g�����h�Ɠ��������̐��������o�����Ƃɂ��܂��D �u���[�v�Ɂg�����Ă���h�L�������v�E�E�E�Ƃ��������ł��D ����𐔎��ŕ\���ƁC���[�v��̔��������C�u���f�F ds �v�Ɠ��ς��Ƃ�`�ɂȂ�܂��D �i����́C���ꂢ�ȉ~�`�̎������x��ɂ��Ă���̂ŁC���ς��Ƃ�Ӗ��͓��ɂ���܂��E�E�E�j
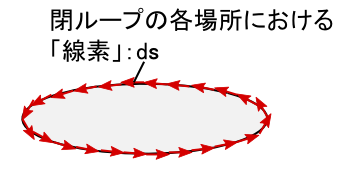
�܂��C�C���e�O�����̓Y������ �gc�h�́C�gcontour integral�h�i����ϕ��j�̓������ł��D ����̂悤�ȁC���[�v�ɉ��������ϕ��̂��Ƃ���Ɏ���ϕ��ƌĂ肵�܂��D �P�ɁC������[�v�ɉ����Ď������x�̒l�����v���Ă��邾���ł��D ���v�Z����u�~�`�̎���̐��ϕ��v�́C�P���� 2��a �������Z���邾���ł��D
���āC�����d�������鎥�����x B ����ϕ�������g4�Ek�EI�h�Ƃ����l�ɂȂ�܂����D �����ŁC�萔 k �i = 1 �~ 10-7 (N/A2) �j �̒��g���C ���̂悤�ɏ��������鎖���l���Ă݂܂��D
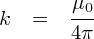
k �̒l�� 1 �~ 10-7 (N/A2) �������̂ŁC ��0�̒l���u4�~10-7 N/A2�v �Ƃ������ƂɂȂ�܂��D���̃�0�́C�u�^��̓������v�ƌĂ��l�ł��D ������Ղ镨����ؖ�����ԁi= �^��j�ɂ�����C�������x�̓͂��₷���E�E�E�Ƃ������j���A���X�ł��D ��0���g���Đ���̕H�ϕ���\���Ă݂܂��D
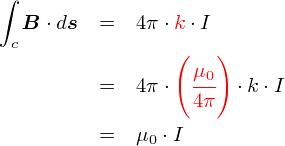
����ƁC�Y���4������܂��D���̂��߂ɂ킴�킴��0��������̂ł����E�E�E�D ����Ȃ킯�ŁC�u�d����������[�v��ɔ��������鎥�����x�̍��v�v�́C ���̎��ŕ\�����Ƃ��ł��܂��D
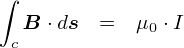
��̎����C�u�A���y�[���̖@���v�Ƃ�����ł��D �₽��ƃL���C�Ȏ��ɂȂ�܂������C���̗��ɂ́u�P�A���y�A���������ꂢ�ɂȂ�悤�Ɍ��߂��v�Ƃ��C �u4�������悤�Ƀ�0�������v�Ƃ��C���\�D������Ȃ��Ƃ�����Ă���킯�ł��D�D�D �Ƃ͂����C�S�̂Ƃ��Ă�����Ɛ�������ۂ��Ă���̂ŁC�S�����͂���܂���D
�r�I�E�T�o�[���̖@���̃A�t�^�[�P�A�Ƃ�����ł͂���܂��C �u�萔 k = ��0/4�v���C���Ƃ��Ƃ̃r�I�E�T�o�[���̖@���ɓ���Ă݂܂��D
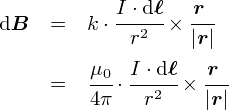
�͂��D��̎����C���ȏ��Ȃł悭�ڂɂ���`�̎��ł��D ���낢������]�Ȑ܂��o�āC�㎮�̂悤�Ȍ`�ɂ܂Ƃ܂����Ȃ��E�E�E�Ƃ����C�����Œ��߂Ă����܂��D
���āC����� ���s�d���ɂ͂��炭�͂Ɓu�A���y�A�v�̒�` �ł́C�u�P�A���y�A�v�Ƃ����d���ʂ��������ꂢ�ɂȂ邩���Ƃ��������`�x�[�V�����Ō��肵�܂����D �{���ɂ���ő��v�Ȃ́E�E�E�H �Ƃ����C���ɂȂ�܂��D
���ہC�u�P�A���y�A�v�����ꂢ�Ɍ��肵�����ƂŁC�^��̗U�d����0���u4�~10-7 (N/A2) �v �ƁC���ꂢ�Ȓl�ɂȂ��Ă��܂��D �������C�u����v�݂̂ł͂Ȃ��u�d��v�܂Ŏ�����L����ƁC ����̒P�ʂ̌�����@�ł͑S�Ă̕����ʂ����ꂢ�Ȑ����ɂȂ�킯�ł͂Ȃ��E�E�E�Ƃ�������������܂��D

�d�C�ʂ̒P�ʁu�N�[���� (C) �v�́C�u1 A �̓d���� 1 �b�ԗ������Ƃ��ɗ����d�C�ʁv �Ƃ������ɒ�`����Ă��܂��D ����ƁC�u�N�[�����̖@���v�́C�u�d�C�ʁv�Ɓu�́v�����т���萔 �i��0 �F �^��̗U�d���j�ł��܂���ɒ��K�����킹��K�v���o�Ă��܂��D ���ہC��0 = 8.854... �~ 10-12 (N-1�EC2�Em-2) �ƁC ���Ȃ�S�`���S�`�������l�ɂȂ��Ă��܂����C����͑S�Ă̂������0�ɗ������ʂł��D
���Ȃ݂ɁC������u�A���y�[���̖@���v�͎������x B ���g���ϕ��h����Ƃ������e�ł������C �g�ʐϕ��h����Ƃǂ��Ȃ�̂ł��傤���E�E�E�H ����́C�����y��Q���z����Ɋւ���@���i�ϕ��`�j�ň��������e�ł��D �������x��ʐϕ�����ƁC�[���ɂȂ�̂ł����D������m�F���Ă����܂��D
���[�v��̎������x B ���C�K���ɕȖʂň͂ރC���[�W���Ă݂܂��D�������x�S�̂��Ȗʂ̒��ɂ����ۂ�Ɠ����Ă���ꍇ�C ���������Ȗʂ��ђʂ��鎥�͐��͖����̂ŁC�ʐϕ��̒l�̓[���ɂȂ�܂��D
�t�ɁC�������x�̃��[�v���Ȗʂ��ђʂ���V�`���G�[�V������z������ƁC ���̎��̂悤�ɁC�u�o��v���͐��Ɓu����v���͐��̖{���͓����ɂȂ�܂��i�������x�̓��[�v���Ă���̂Łj�D ����āC��͂�ʐϕ��̒l�̓[���ɂȂ�܂��D
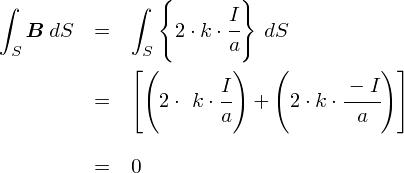
�ȏ�ŁC�������x�Ɋւ��@���͈�ʂ�m�F�ł��܂����D ���́C�����ƕۗ����Ă����u���� H�v���u�������x B�v�̈Ⴂ�ɂ��ĊȒP�ɐG��܂��D
���āC�u�A���y�[���̖@���i�ϕ��`�j�v�͈ȉ��̂悤�Ȏ��ł����D ���܂���Ƃ���������������܂��C���̎��ɏo�Ă����u�������x B �v�Ƃ����̂́C �u�d���ɗ͂��y�ڂ���v�ł��D
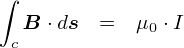
�d���C�w�̋��ȏ���ǂ�ł���ƁC�������x�Ǝ����悤���u���� H �v�Ƃ�����ɂ��ڂɂ����邱�Ƃ�����܂��D ���̎���Ƃ����͉̂��҂Ȃ́E�E�E�H�Ƃ����b��������Ƃ��Ă����܂��D
�܂��C���̐}�̂悤���u�R�C���v���C���[�W���܂��D �R�C������鎥��������Ɍv�Z����Ƃ���͏ȗ����܂����C�R�C���ɓd���𗬂��ƃR�C�����ђʂ���悤�Ȏ������x�������܂��D ����́C�啔���̐l���q���̂���Ɏ������Ă���Ǝv���܂��D�D�D
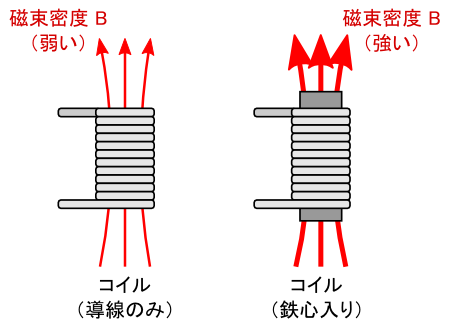
�����āC�R�C���̒��S���u�S�S�v������ƁC�R�C�������鎥�����x����������܂��D ������C���Ȃ��݂̎������Ǝv���܂��D �����ŁC�ǂ����Ă����Ȃ�́H�Ƃ������Ƃ��l���Ă݂܂��D
�u�S�S�v�͓S�łł��Ă���킯�ł����C�S�̒��ɂ͑�R�̓d�q�������Ă��܂��D ���̓d�q�̓����́u�d�ׂ̓����v�Ƃ������ƂŁC�u�d���v�Ɠ����Ȃ��̂ƍl�����܂��D �d��������Ƃ������Ƃ́C����ɂ���Đ������u�������x�v������͂��ł��D
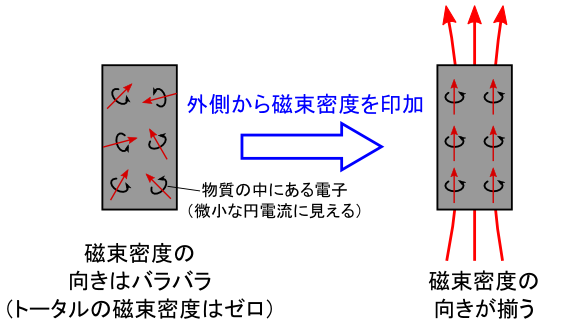
�������Ȃ��畨���̒��́u�d�q�̓����̌����v�́C���ʂ̓o���o���ł��D ��ʂ̓d�q���o���o���Ȍ����̎������x�������Ă���̂ŁC �g�[�^���Ō���ƁC�����̊O���ɏo�Ă����������x�̓[���ɂȂ�܂��D �������C�������O�����畨���Ɏ������x����������ƁC �������̓d�q�����̎������x�̗͂��C�Y��ɐ��邱�ƂɂȂ�܂��D
���́u����v�̂��₷���́C�����ɂ���ėl�X�ł��D �u�S�v�͓��ɐ��₷���̂ŁC��苭���������x�������邱�Ƃ��ł��邽�߁C�R�C���̐c�Ƃ��Ă悭�p�����܂��D
����Ȃ킯�ŁC�u�S�S����R�C���v�̎���̎������x�́C �u�d��������I���W�i���Ȏ������x�v�ƁC �u�S�S�����鎥�����x�v�����킹�����̂ɂȂ�܂��D ���̓S�S�����鎥�����x�Ƃ����̂́C���ǂ��ł����C�O���̎������x�i= �d�������������鎥�����x�j�ɉe������Đ��������̂ł��D
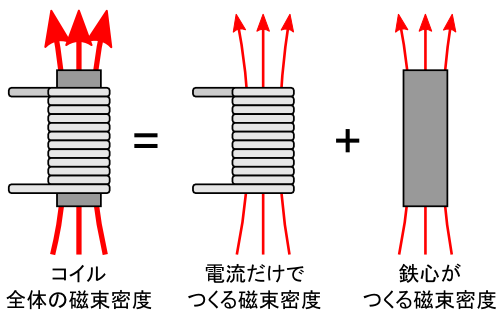
����𐔎��ŕ\���ƁC���̂悤�ɂȂ�܂��D
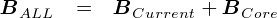
�gBALL�h�Ƃ����̂��S�̂̎������x�C �gBCurrent�h���d�������鎥�����x�ŁC �gBCore�h�͓S�S�ɂ�鎥�����x�ł��D �����ŁC���ʂ́u�������x�v�Ƃ������̂̓��[�v��̏�ł��D ����u�P�_�v�ɂ����鎥�����x���l������́C ���[�v�ɉ����Ă�����Ɛ��ϕ������ق����C �d��������u�g�[�^���̎������x�v�̃C���[�W�ɋ߂��Ȃ�܂��D ����Ȃ킯�ŁC��̎��𗼕ӂ��C�Ƃ肠�������ϕ������`�ɏ����Ă����܂��D
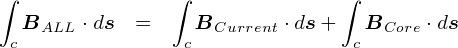
�����ŁC�O�ɂ������u�A���y�[���̖@���v���v���o���܂��D
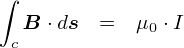
�u�d������鎥�����x�̐��ϕ��v�́C�g��0I�h�ɓ������̂ł����D �����������ƁC���̂悤�ɂȂ�܂��D
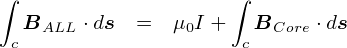
�����ŁC�gBCore�h�Ƃ�����́C ���Ƃ��Ɠd��������u�����O���̎������x�v�ɉe������Đ������̂ł����D ���̓_���ӎ�����ƁC�gBCore�h�̑傫���́C �O���̎������x�̑傫���ɂ���č��E��������ƂɂȂ�܂��D ������C�����ŕ\���Ă݂܂��D

��̎��́C�u�������琶���鎥�����x�́C���̎���ɂ���i�d��������j�������x���g���h����v �ƌ����Ă��܂��D ����͂��Ȃ�P��������b���Ɗ����邩������܂��C �F�X�ȕ����Ŏ������Ă݂�ƁC�ӊO�Ƃ��̋ߎ��͎��p�I�Ȃ悤�ł��D ���̔��萔�g��m�h�́C �u�������v�imagnetic susceptibility�j�ƌĂ�邻���ł��D�������̕����ʂł��D
���ǂ̂Ƃ���C���ׂĂ̍��������u�d�������鎥�����x�v�Ȃ�ł��D ����Ȃ킯�ŏ�̎����C����ł���u�d���v�����ɏo�Ă���悤�ɕό`���Ă݂܂��D �܂��́C���S�̂���ϕ����܂��D
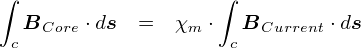
�����ʼnE�ӂɃA���y�[���̖@�����g���ƁC���̂悤�ɏ��������邱�Ƃ��ł��܂��D
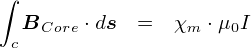
�u�������̎������x�́C�O���̓d�����e�������v�Ƃ������Ƃ�������₷�����ɂȂ��Ă��܂����D
������C�u�S�̂̎������x�̎��v�ɑ�����܂��D ���łɁC�A���y�[���̎���������Ă��܂��܂��D����ƁC
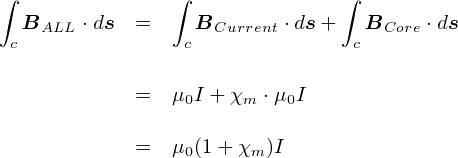
�E�E�E�Ƃ������ƂŁC�u�g�[�^���̎������x���C���ǂ͓d���������Ă���v�Ƃ����C���[�W��\���܂����D �����ŏo�Ă����C�d�� I �Ǝ������x B �����т�����萔 �g��0(1+��m)�h �̂��Ƃ��C�i����������ꍇ�́j�u�������v�imagnetic permeabiity�j �ƌĂт܂��D �g(1+��m)�h�̕����͖������ʂł����C ���̕������������o���āC�u�䓧�����v�ƌ������肷�邻���ł��D
�����܂ł̘b�ŁC�ȉ��̎��������܂����D
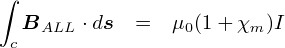
����͂���ŁC�u�d�����������x������v�Ƃ���������\���Ă��ėǂ��̂ł����C �g��m�h�̒l�́C�d���̎���ɂ��镨���ɂ���ăo���o���ł��D ����ƁC�d����������ɂ���āC���̎���ɐ����鎥�����x�̒l���o���o���ɂȂ��Ă��܂��܂��D �܂�C�u�����d���ʂ��Ƃ��Ă��C���̎���̏ɂ���Đ������i�������x�j�̑傫���͈قȂ�v �Ƃ����C���X��₱�������ƂɂȂ�܂��D
���l���Ă���u�}�N�X�E�F���������v�́C�d���C�̏����ۂ��܂Ƃ߂��g�ǂ��ł��ʗp��������h�݂����Ȃ��̂Ȃ̂ŁC ���́u���ɂ���Ēl���ς��v�Ƃ����͍̂D�܂�������܂���D�D�D �ǂ��������u�ǂ��ł��ʗp��������v�ɂȂ�̂��l���Ă݂܂��D
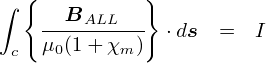
��̎��́C�P���ɁC�������̎��̗��ӂ��g��0(1+��m)�h�������������ł��D �Ƃ͂����C���̎��̉E�ӂ͂����́u�d�� I�v������Ă���̂ŁC ���ӂ̗ʂ��C�u�����ɂ���d���̒l�����Ō��܂�v�ƌ��������ł��D
����Ȃ킯�ŁC���́u�������x�����Ŋ������l�v�́C �u�d���̒l�݂̂ɂ���Č��܂�v�Ƃ����Ӗ��ŕ֗��Ȃ̂ŁC���O��t���邱�Ƃɂ��܂����D ���ꂪ�u���� H �v(magnetic field) �Ƃ�����ɂȂ�܂��D ����̒P�ʂ� (A/m) �ł��D

���� H �́C�d���̒l�݂̂ɂ���Č��܂�l�ŕ֗��ł����C ���������������̘b�ł����u�d������g�́h�v�Ƃ͊W������܂���D ����́C�d�� E ���g�́h�Ɋւ���ł������̂ɑ��āC �u�d�����̖{�����l���₷������v�Ƃ������R�œd�����x D ����������Ɏ��Ă��܂��D �d�� E �͎������x B �ƑΉ����Ă���C�d�����x D �͎��� H �ƑΉ����Ă��܂��D �g���x�h�Ƃ������O���H������Ă���悤�Ɍ����܂����C����͗�ɂ���ė��j�I�ȗ��ꂪ�W���Ă���̂ŁC �l�[�~���O�Ɋւ��Ă͂��傤���Ȃ��i�H�j����Ă����܂��D
���Ȃ݂ɁC�����܂łЂ�����߂��S�̂̓������g�ʁh���g���ƁC�������x�Ǝ���̊W�͎��̎��ŕ\���܂��D
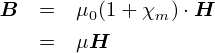
���ɁC�u�^�v�ł́C �]�v�ȕ����͉��������Ƃ������ƂȂ̂ŁC�g��m = 0�h�ɂȂ�܂��D ����ƁC�g��0(1+��m�j�h�̕����͂����́g��0�h �ƂȂ�܂��D ����Ȃ킯�ŁC �g��0�h�̂��Ƃ��u�^��̓������v�ƌĂԂ悤�ɂȂ��������ł��D �^�ł́C�������x B �Ǝ��� H �͈ȉ��̊W�ɂȂ�܂��D
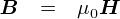
�O�ɂ����Ă����A���y�[���̎��ɁC��̊W�������Ă݂܂��D
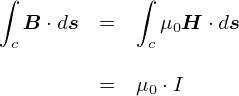
��0�ŗ��ӂ�����Z���邱�ƂŁC�ȉ��̎����������܂��D
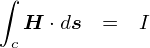
���ǂ��ł����C�u���� H �v�͓d������͂Ƃ͊W����܂���D �������C�㎮�̂悤�Ɏ������ꂢ�ɂȂ�̂œ�������܂����D ���̎��́C�d�� I �̎���ɂǂ�Ȕ}�������݂��Ă����藧���ƂɂȂ�܂��D ���̂��߁C���̂��ꂢ�Ȏ��̕����u�A���y�[���̖@���v�ƌĂԂ��Ƃ����X����܂��D
�Ƃ肠�����C����Ń}�N�X�E�F���������̑�R���̔������������܂����D �Ō�ɁC�c�����������������邱�Ƃɂ��܂��D
�����܂ł̘b�ŁC�u�d���̎���ɂ͎��ꂪ�ł���v�Ƃ������Ƃ��������Ă��܂��D
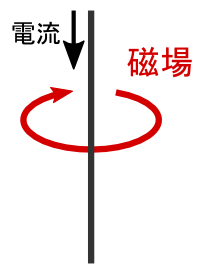
���̎���̗l�q��\�����������C�u�A���y�[���̖@���v�ł����D
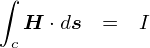
�ł͂����ŁC�[�d���́u�R���f���T�v��z�����Ă݂܂��D
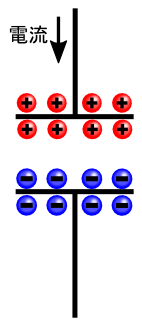
�R���f���T�͋ɔԂ��≏����Ă���̂ŁC�d���𗬂��n�߂Ă��玞�Ԃ��o�ƁC �d��������Ȃ��Ȃ�܂��D �������C�d�����~�܂�܂ł̏�ԁi�ߓn��ԁj�ł́C�������������ɔɓd�ׂ߂邽�߂ɓd������u����܂��D ���́u��u�v�ɒ��ڂ��܂��D
���ʂɓd��������Ă���d���̎���ɂ́C���R�ł����C�ǂ��̏ꏊ�ł����ꂪ�����Ă��܂��D ����ɑ��ăR���f���T�ł́C�ɔ̏㉺���u�d���v�ɂ͕��ʂɓd��������Ă�����̂́C �u�ɔ̊ԁv�ɂ͓d��������Ă��܂���D �d�ׂ̗����ɂ���ċɔɒ~������d�חʂ��ω�����킯�ł����C�g�ɔ̊Ԃ�d�ׂ��s��������h�Ƃ������Ƃ͖����킯�ł��D ����ƁC�u�ɔ̊Ԃɓd���������Ȃ�C����������Ȃ��́H�v�Ǝv���Ă��܂��܂��D �������C�����l���Ă��܂��ƁC�ɔԂ����A�������Ƃ���Ă��܂��āC�Ȃ��s���R�Ȋ��������܂��E�E�E�D
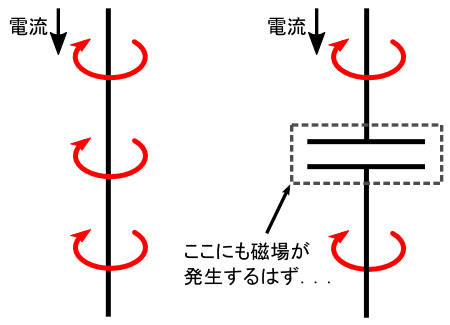
�ł́C�d���ȊO���u�ɔԂɑ��݂���g�����h�v��T���Ă݂邱�Ƃɂ��܂��D
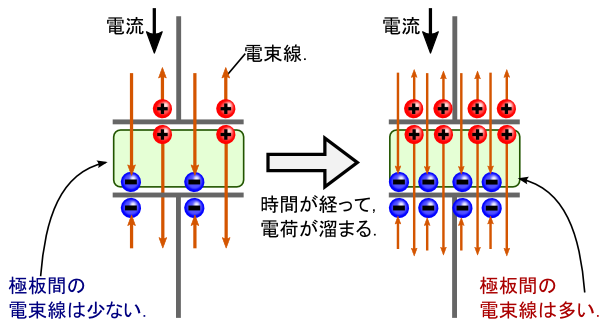
�R���f���T�ɓd�������ꍞ�ɔɓd�ׂ����܂�ƁC �ɔԂ̓d�����̖{�����ω����܂��D �����ŁC�u�d�����v�Ƃ����̂́C�P�N�[�����̓d�ׂ���P�{�ł�Ƃ�����ł����D �d�ׂ̐����ω�����C���R�ł����C�d�����̖{�����ω����܂��D �u�P�N�[�����̓d�ׂ���P�{�v�Ƃ����C���[�W��������₷���̂ŁC�����ł͓d�� E �ł͂Ȃ� �d�������g���ĒP���ɃC���[�W���܂����D
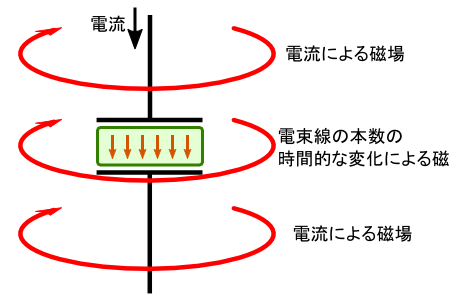
�����ŁC�u�d�����̎��ԓI�ȕω��ɂ���Ă�����͔�������v �E�E�E�ƍl����ƁC �d���̕����ł��R���f���T�̋ɔԂł��C���̎���Ɏ��ꂪ�������邱�ƂɂȂ�܂��D ����ƁC���ꂪ�r���Ŗ����Ȃ�E�E�E�Ƃ����C�����������Ƃɂ͂Ȃ炸�C ���ʂ��������ɂȂ�܂��D �Ƃ肠�����C���̍l�������̗p���Ęb��i�߂邱�Ƃɂ��܂��D
�ł́C�u�d�����̖{���̎��ԕω��v�Ƃ�����𐔎��ŕ\�����Ƃ��l���܂��D �܂��́C�u�d�����x D �v�̎��ԕω������ŕ\���Ă݂܂��D

�Δ����ɂȂ��Ă���̂́C��ʓI�ȓd�����x D �̒l���ꏊ(x, y, z)�Ǝ���(t)�C�S�̕ϐ�������������ł��D ��̃R���f���T�̐}�ł͓d�����x D �͋�ԓI�Ɉ�l�ł����C��ʓI�ɂ͊e�ꏊ(x, y, z)���ƂɈ�����l�ł��\���܂���D
���ɁC�u�ɔԂɂ���S�Ă̓d�����̖{���v�̎��ԕω����l���܂��D ����́C���̎��̂悤�ɖʐϕ����邾���ł��D �������C�����I�ɈӖ��̂���d�����͍l���Ă���ʂɑ��Đ����Ȑ��������Ȃ̂ŁC ���Ȃ��݁u�@���x�N�g�� n �v�Ɠ��ς��Ƃ��Ă��܂��D
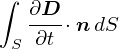
�ł́C�O�ɂ������u�A���y�[���̖@���v�ɁC �u�d�����̖{���̎��ԓI�ȕω�������������v�Ƃ����Ӗ����������Ă�邱�Ƃɂ��܂��D ����͒P���ɁC��̎����A���y�[���̖@���̉E�ӂɉ����邾���ł��D
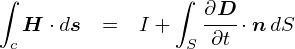
��̎��́C �u�A���y�[���E�}�N�X�E�F���̖@���v �ƌĂ����̂ŁC ���̎����g������̃R���f���T�̘b�̂悤�ɁC �d�����ǂ����œr��Ă��Ă��A���������ꂪ�����邱�Ƃ�����ł��܂��D �A���y�[���̖@���̉��ǔłƂ������Ƃ���ł��D
���炽�߂āC���������u�A���y�[���E�}�N�X�E�F���̖@���v�߂Ă݂�ƁC �g�d���h�Ɓg�d�����̎��ԕω��h�������Z����Ă��܂��D �u�����Z�v�Ƃ����̂́C�Q�̕����ʂ������ȏꍇ�����\�Ȃ��Ƃł��D �������C�u�g�d���h�Ɓg�d�����̎��ԕω��h�͓����悤�Ȋ����̂��̂Ȃv�ƌ����Ă��C�s���Ƃ��Ȃ��Ƃ���ł��D�D�D ���̕ӂ̘b���@�艺���Ă݂܂��D
�܂��C�u�P�N�[�����v�Ƃ����ʂ́C�ǂ�����Č��߂��Ă����̂����v���o���Ă݂܂��D
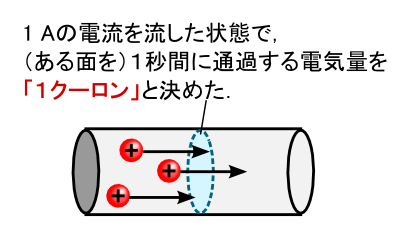
���������u�d�C�ʁv�i�P�ʂ̓N�[�����j�Ƃ������̂́C �d�������Ƃɂ��Ē�`���ꂽ�ʂł����D �P A�̓d�����P�b�ԗ��������ɒʉ߂���g�[�^���̓d�C�ʂ��C �u�P�N�[�����v�ł��D ���̂��߁C�P�ʂɖڂ�������ƁC�u (C) = (A�Es) �v�Ƃ������ƂɂȂ�܂��D
���̓d�C�ʂ̒�`����C�d�������ԂŐϕ�����u�d�C�ʁv�������邱�Ƃ�������܂� �����ŕ\���Ǝ��̂悤�ɂȂ�܂��D
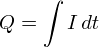
�����ŁC�u�K�E�X�̖@���i�ϕ��`�j�v�Ƃ�������v���o���܂��D ���̂悤�Ȏ��ł����D
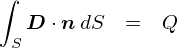
���̎��́C�u�d��Q����o��d�����̖{�������v����ƁCQ�{�ɂȂ��v�Ƃ����Ӗ��ł����D ���̎����C�������̓d���Ɠd�ׂ̊W�̎��ɑ�����Ă݂܂��D
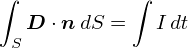
��̎��ŁC����Ɓu�d���v�Ɓu�d�����x�v�����т��܂����D ���Ƃ́C��̎��̗��ӂ����ԂŔ������Ă��܂��D
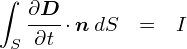
�E�E�E�Ƃ������ƂŁC�u�d���v�� �u�d�����̖{���̎��ԕω��v�͓����ł��邱�Ƃ�������܂����D ���ۂɓd�ׂ̈ړ��������Ă��C ���̏ꏊ�̓d�����x���ω�����i�܂�C�d�ꂪ�ω�����j���Ƃ�����C ����������I�ɓd��������Ă����ƌ��Ȃ���Ƃ������ƂɂȂ�܂��D ����Ȃ킯�ŁC�u�d�����ۂ��v�Ƃ����C���������߂āC ���̓d���̎��ԕω��̂��Ƃ��C�u�ψʓd���v�idisplacement current�j �ƌĂԂ����ł��D
�A���y�[���E�}�N�X�E�F���̖@���ł� �u�d���ƕψʓd���̗������C��������錴���ɂȂ��v�ƌ����Ă���킯�ł��D
���āC���X�Ǝ���̘b�𑱂��Ă��܂������C �悤�₭�����ł̎����ł��܂����D
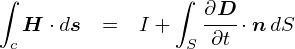
���ǂł����C��̎��̈Ӗ��́C�u��������̂́C�d���ƕψʓd���ł���v�Ƃ����Ӗ��ł��D �����ŁC�u�d���v�̕������C�d�����x�̖ʐϕ��Ƃ��ď��������Ă����܂��D ���̕������ϕ��̌`�Ȃ̂ŁC�d������ �gI�h �Ƃ����̂��ȂA���Ȃ̂ŁD�D�D
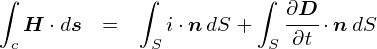
��ʓI�ɏ�̎��̂��Ƃ��C�u�}�N�X�E�F���������̑�R���i�ϕ��`�j�v�ƌĂт܂��D ���̎��̕ʖ��́C�u�A���y�[���E�}�N�X�E�F���̖@���i�ϕ��`�j�v�ł��D
�}�N�X�E�F���������̑�R���C �A���y�[���E�}�N�X�E�F���̖@���́u�����`�v�ł��D �u�d����ψʓd�����C����������v �Ƃ����b�ł��D
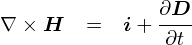
�u����v�ɂ��Ăׂ̍����b����R���F�A���y�[���E�}�N�X�E�F���̖@���i�ϕ��`�j�̂Ƃ���ň�ʂ�ς܂����̂ŁC ����͐ϕ��`�ō���������u�����`�v�ɍ��ς����Ƃ����ł��D
�O�ɏo�Ă����A���y�[���E�}�N�X�E�F���̖@���̐ϕ��`�Ɠ������C ����͎������x�i����j�ł��D �ϕ��`�̏ꍇ���u���[�v��̎���S�̂�������Ɛ��ϕ�����v�Ƃ����C �L���͈͂̎����ɂ��Ă��܂����D ����ɑ��č���̔����`�ł́C�u�����_�ɂ����鎥��̉Q�i���[�v�j�v���l���邱�ƂɂȂ�܂��D
���Ȃ��݂ł����C���� H ��d�� I �C�d�����x D �Ƃ������e�p�����[�^�͏ꏊ (x, y, z)�� ���� (t) �̊��ƂȂ��Ă��܂��D ���J�ɏ����Ə�̎��̂悤�ɂȂ�܂����C��̂��Ƃ��C����͏ȗ����܂��D
���ꂩ��̓��e����������Ƃ܂Ƃ߂܂��D
����́u�����`�v�Ȃ̂ŁC����P�_�ɂ����鎥�������Ă������ƂɂȂ�܂��D �O����R���i�ϕ��`�j�Ŋm�F�����ʂ�C���� H�⎥�����x B�Ƃ����̂� ���[�v�����Ăł����i�Q���j�Ȃ̂ł����D ����Ȃ킯�ŁC���ꂩ��l���鑊����u����P�_�ɂ�����Q�v�Ƃ������ƂɂȂ�܂��D
�����͌����Ă��C�u�_�ɂ�����Q�v�Ȃ�Ă��̂��C���[�W����͓̂���ł��D ���������u�Q�v�Ƃ����̂� �u������x�̑傫�����������ʂ̃t�`�ɉ����āC������Ɖ����́v �Ƃ����C���[�W�ɂȂ�킯�ł����C �u�����̓_�v�̂܂܂ł̓t�`���l���邱�Ƃ��ł��܂���D �����ŁC�u����_�ɂ�����Q�v�Ƃ�������C �u�����Ȗʂ̃t�`�ɉ��������[�v�v�ɒu�������Ă��܂��܂��D �����Ȗʐς��Ɍ��܂ŏ���������Γ_�ɂȂ邾�낤�E�E�E�Ƃ����C���Ȃ��ݔ��ϕ��̍l�������g�������ɂȂ�܂��D
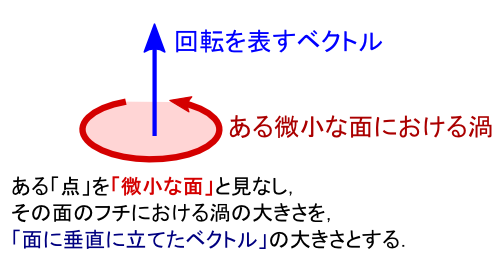
�u�Q�i��]�j�̌����v��\����i�ł����C ����͗�̂��Ƃ��E�l�W�������ƁC�E�l�W���i�ޕ����ɑΉ������Ă��܂��̂��֗��ł��D �u�Q�v�Ƃ����͕̂��ʏ�ɂ�����̂ł����C���̕��ʂɐ����ɗ��Ă��x�N�g�����u�Q��\���x�N�g���v�Ƃ��Ďg���܂��D ����̉Q�̌����ɉE�˂��������ɁC�E�˂����i�ތ����Ƀx�N�g����L���܂��D
�x�N�g���̌�����������C����ƂP�P�Ή��Łu�Q�̖ʁv�����܂�܂��D ����ɁC���̃x�N�g���̒������u�Q�i��]�j�̑傫���v��\���ƌ��߂Ă��܂��C �x�N�g���P�{�Łu�Q�̑傫���ƌ����v���ɕ\�����Ƃ��ł��Ċy�ł��D ����Ȃ킯�ŁC���̓x�N�g���P�{�Łu�Q�i��]�j�v��\���̂��퓅��i�ɂȂ��Ă���悤�ł��D ���́C�u�g��]�h���x�N�g���P�{�ŕ\���v�Ƃ����C���[�W�͔��ɏd�v�ŁC ��X��������o�Ă���l�����ł��D
���āC����ł͋�̓I���u��������Ȗʂ̃t�`�ɉ������Q�v�����ŕ\�����Ƃ��l���Ă݂܂��D �u�Q�v�̑傫���́C���̃t�`�ɉ��������ϕ����v�Z���邱�Ƃ��ł���̂ł����D �u�A���y�[���̖@���i�ϕ��`�j�v�ōl�����̂Ɠ����b�ł��D
�����ł͊�{�I�ȍ��W�Ƃ��ĉ��}�̂悤��x-y�̍��W��~���āC�l�p���t�`�Ōv�Z���邱�Ƃɂ��܂��D
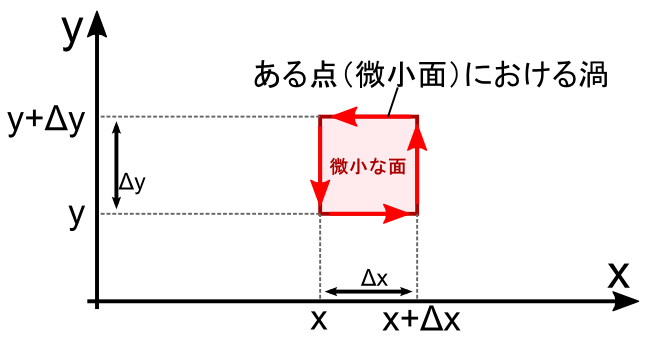
��̐}�̂悤�ɁC�u�Q��v�ł��鎥�����x B �́C�e�ꏊ�ɂ����ăo���o���Ȍ����C�o���o���傫���ƂȂ��Ă��܂��D ����������������璭�߂�Ɓu�S�̂Ƃ��ĉQ�������Ă���悤�Ɍ�����v�Ƃ��������ł��D
�Q�𐔎��ŕ\�����@�́C�u�ʂɐ����ȃx�N�g�����g���ĕ\���v�Ƃ������ƂɂȂ��Ă��܂����D �����xy���ʂɉQ������̂ŁC���̉Q��\���x�N�g����z�������ɐL�т邱�ƂɂȂ�܂��D
�ł́C��̓I���u�Q�̌`�������������x B �̐��ϕ��v���v�Z���܂��D
������₷�����邽�߂ɁC�u���ϕ��v�����ꂼ��̕ӂ��Ƃɕ����Čv�Z���邱�Ƃɂ��܂��D �Ō�ɑS���̕ӂɂ��č��v����C�Q�S�̂̐��ϕ������܂�E�E�E�Ƃ�������ł��D �P�̕ӂ̐��ϕ��́C�ȉ��̂悤�ɂ��Čv�Z���܂��D
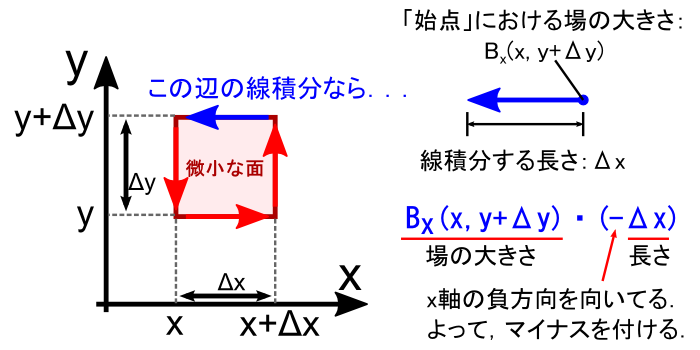
�e�ӂŐ��ϕ������鎞�C�ŏ��ɃX�^�[�g�n�_�i�n�_�j�����߂܂��D �n�_�̌��ߕ��͔C�ӂł��D �����āC���Ȃ����u�g���̏ꏊ�ɂ������̑傫���h�~�g�o�H�̒����h�v�Ő��ϕ��̒l�����߂܂��D �������C����́u�o�H�̒����͔��ɒZ���g��x�h�v�Ƃ������Ƃɂ��Ă���̂ŁC �u��x�̋�ԓ��ł͎������x B�̑傫���͕ς��Ȃ��v�ƍl���Ă��܂��܂��D ���ϕ��ł悭�o�Ă���l�����ł��D ����ɂ���āC���ϕ��͒P�����u�g�n�_�ɂ������̑傫���~�g�o�H�̒����h�v �Ōv�Z���邱�Ƃ��ł��܂��D
����Ȃ킯�ŁC�S�Ă̕ӂɂ��Đ��ϕ������߂�ƁC�ȉ��̂悤�Ȋ����ɂȂ�܂��D
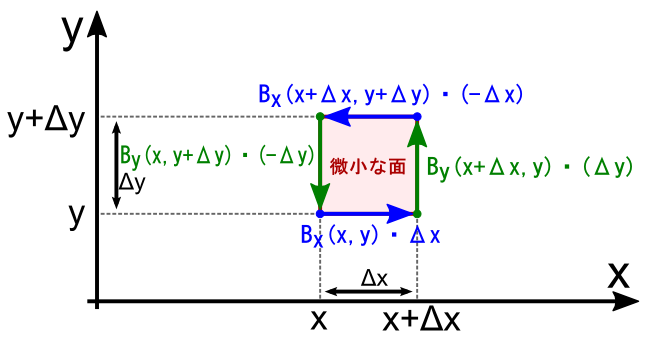
x�����̎������x���uBx�v�ŁC y�����̎������x���uBy�v�Ƃ��Ă��܂��D �����xy���ʏ�̎������x�̏���l���Ă���̂ŁC�Ƃ肠�������̂Q�ŕ\�����邱�Ƃ��ł��Ă��܂��D z�������̎������x���l����K�v������ꍇ�i���Ƃ���yz���ʓ��̉Q�j�́C �uBz�v���g���K�v������܂��D�D�D
��̐}����C������u�����ʂ̃t�`�ɉ��������ϕ��v�́C���̎��ŕ\���܂��D �P���ɁC�����Z���邾���ł��D
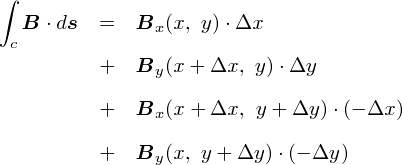
��̎��́C���h�Ɂu�����ʂ̃t�`�̉��������ϕ��v�ɂȂ��Ă��܂��D �����C���W���gx+��x�Cy+��y�h�ȂǂƂȂ��č��ݍ����Ă��āC�������X�S�`���S�`�����Ă��܂��܂����D Bx��By�̎n�_�̎��������������H�v���āC ���̃X�e�b�v�Ɍq���鏀�������Ă����܂��D �i��ŏo�Ă��܂����C�Δ��������₷�����邽�߂̍�Ƃł��D���w�I�ȏ����̃e�N�j�b�N�ł��D�D�D�j
�܂��́C�l�p�`�̏㑤�̕ӂɂ��Ăł��D �������͎n�_���E���̒��_�ɂƂ��Ă��܂������C����������̒��_�ɕύX���܂��D
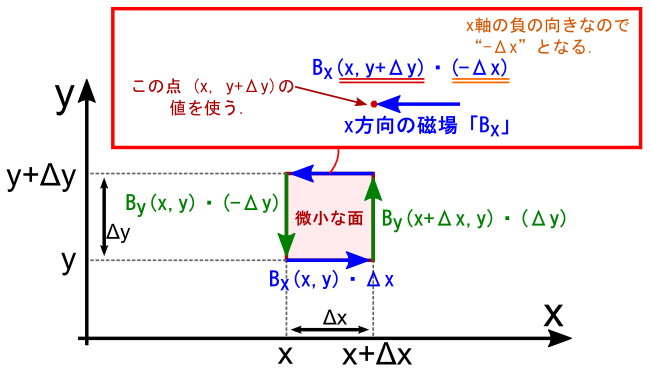
���̏ꍇ�Cx�����̎������x�̑傫�����uBx (x�Cy+��y)�v���g�����ƂɂȂ�܂��D ���ϕ��̕����C�����͓����Ȃ̂Łu-��x�v�̂܂܂ł��D �u����ӂ̒��ʼnE�[�̒l���̗p���悤�ƁC���[�̒l���̗p���悤�ƁC �قƂ�ǒl�͕ς��Ȃ����낤�v�Ƃ����C���������ςȁi�H�j���ϕ��̃Z���X�ł��D �Ƃ肠�����C����ŁuBx (x+��x�Cy+��y)�v���������̂��uBx (x�Cy+��y)�v�ɂȂ�܂����D �������������ȒP�ɂȂ�܂��D
����ɁC�����ЂƂD���x�͉E���̕ӂɂ��Ăł��D ������C�n�_�̈ʒu��ύX���Ă��܂��܂��D
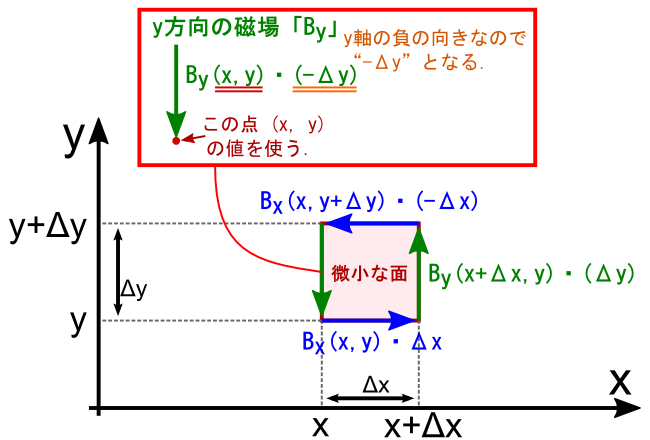
���Ƃ��Ƃ��̕ӂ̐��ϕ��́C�n�_���㑤�̒��_�ɂƂ��Ă��܂����D ����������̒��_�̒l�ɕύX���܂��D �������x�̒l���uBy (x�Cy)�v���g�����ƂɂȂ�܂��D ����ŁC�uBy (x�Cy+��y)�v���������̂��uBy (x�Cy)�v�ɂȂ�܂����D
���炽�߂āC�e�ӂ̐��ϕ��̒l���m�F���Ă����܂��D
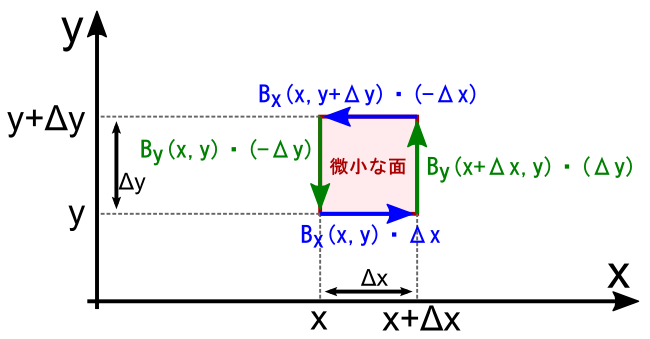
����Ȃ킯�ŁC���̃��[�v��������ƂP��������ϕ��̒l�́C���̎��ŕ\����܂��D
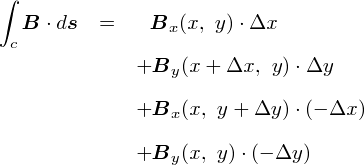
����ŁC�u�P�_�ɂ�����Q�̑傫���v�����߂����ƂɂȂ�܂��D ���ǂ��ł����C���̂Ƃ��Ắu�����ʐς̃t�`�ɉ������C�Q�̐��ϕ��v�ł��D �����C���́u�����ʐρv�i��̎��ł����Ɓg��x�E��y�h�ł��j�����ɏ������C���[�W�Ȃ̂ŁC ���������g�_�h���낤�E�E�E�Ƃ������Ƃł��D
����P�_�ɂ�����Q�̐��ϕ������܂����̂ŁC���́u�����`�̃A���y�[���̖@���v����邱�Ƃɂ��܂��D
���āC����܂ł̘b�Łu����P�_�ɂ�����Q����ϕ��������ʁv�Ƃ����̂́D ���̎��ŕ\���邱�Ƃ��������Ă��܂��D
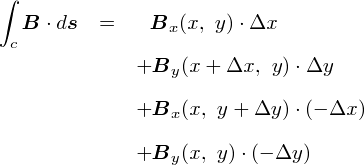
��̎��́u���ϕ��v�̎��Ƃ������������āC �܂��u�ϕ��`�v�̃C���[�W���甲���o���Ă��܂���D�D�D ���ꂩ��C���~�����u�����`�v�̃C���[�W�ɋ߂Â��邽�߂� ������ό`���Ă�����Ƃ����܂��D
�Ƃ肠�����C�g��x�h�Ɓg��y�h�ʼnE�ӂ��������Ă݂܂��D
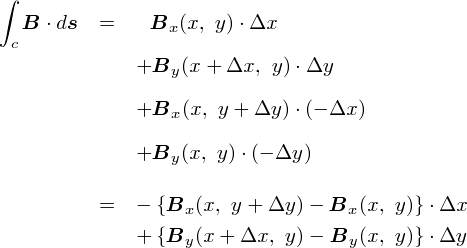
����ɁC���ӂ��g��x�E��y�h�Ŋ���Z���܂��D
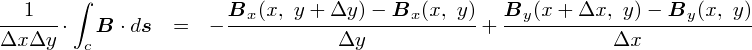
����ƁC�E�ӂɁu�����v�̌`�����̂܂�o�Ă��܂����D ����Ɓu�����`�v���ۂ����͋C�ɂȂ��Ă��܂����D
��̎��ł́CB(x�Cy)�Ƃ��� x �� y �̊����C x �������� y �����Ŕ������Ă���`�ɂȂ��Ă��܂��D ����́C�������u�Δ����v�Ƃ�����ł��D ����Ȃ킯�ŁC�Δ����̋L�����g���ď����Ă����܂��D �i��x��dx�C��y��dy�Ƃ����Ɍ�������Ƃ��Ă��܂��܂��D���ꂪ�C�u�����Ȗʁv���u�_�v�ɏk�����鑀��ł��D�j
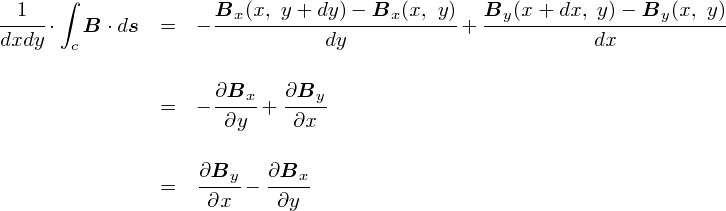
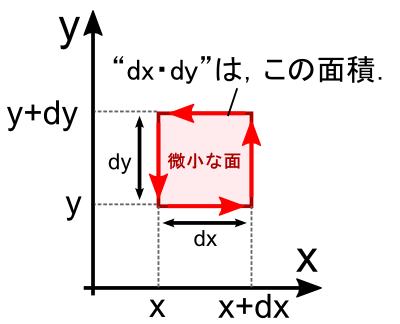
���炽�߂āC���܂ł̕ό`�ŏo�Ă����������Ă݂܂��D
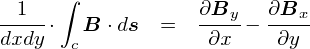
���ӂ́C�Q�ɉ��������ϕ����C�gdxdy�h�Ŋ���Z�����l�ƂȂ��Ă��܂��D ���́gdxdy�h�Ƃ����̂́C���[�v���l�����ʂ́u�ʐρv�������܂��D
���ϕ��̒l�Ƃ����̂́C�u�Q�̋����E�傫���v�Ƃ������Ӗ��������܂��D ��������[�v�̖ʐςŊ���Z���Ă���킯�ł��D �܂�C���ӑS�̂��Ӗ�������̂��u�P�ʖʐς�����̉�]�̗ʁi�Q�̑傫���j�v�Ƃ��������ɂȂ�܂��D �����āC�u�P�ʖʐς�����̉Q�̑傫���v�͉E�ӂ̕Δ����v�Z�ŋ��߂��܂���E�E�E�Ƃ����̂��C���̎��������Ă�����e�ł��D �Ȃ��s�v�c�Ȋ����ł��ˁD
�����܂ŋ��߂Ă����u�P�ʖʐς�����̉Q�̑傫���v�́C���̎��ŕ\����܂��D
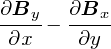
���̒l�ɁC�Q�̑傫�������߂������[�v�́u�ʐρv�������Z���Ă��C �S�̂Ƃ��Ẵ��[�v�̑傫�������߂邱�Ƃ��ł��܂��i�ꏊ�ɂ���ă��[�v�̑傫�����Ⴄ�ꍇ�́C�u�ʐϕ��v���邱�ƂɂȂ�܂��j�D
�����ŁC���́u���[�v�ɂ�����Q�v�̓x�N�g���ŕ\�����[�������������Ƃ��v���o���܂��D
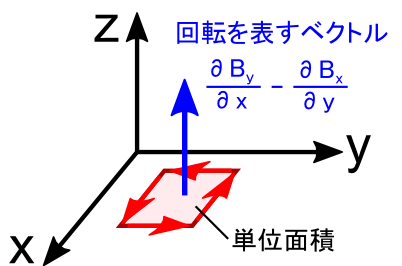
�����xy���ʏ�̃��[�v���l���Ă����̂ŁC�Q�̑傫����\���x�N�g����z�������ɐL�тĂ��܂��D �P�ʖʐς�����̉Q�̑傫�����C���[�W����ƁC���̃x�N�g���̑傫�������߂� �u��By / ��x - ��Bx / ��y�v�ɂȂ�킯�ł��D
����ł́C���́u�Q�̑傫����\���x�N�g���v���R�����Ɋg�����܂��D ���܂܂ł�xy���ʓ��̉Q�������l���Ă����̂ŁC��������L�т�x�N�g����z�����̂��̂����ł����D ����ɑ��āCyz���ʓ��̏ꍇ���ux�������ɐL�т�x�N�g���v�C zx���ʓ��̏ꍇ���uy�������ɐL�т�x�N�g���v�����ꂼ��u��]�ʁv��\�����ƂɂȂ�܂��D �i�Ⴆ�Cxy���ʓ��ɂ����܂�Ȃ��悤�ȁC������ƌX�����������ʂɂ�����Q��\���������ꍇ�C �R�����́u��]�x�N�g���v���K�v�ɂȂ�܂��D�j
x�Cy�Cz �̂R�����ɂ��āC��]�ʂ�\���x�N�g������ׂĂ݂܂��D �ׂ����v�Z�͏ȗ����܂����C��{�͍��܂ł́uxy���ʓ��̉Q�v�Ɠ����v�Z�ł��D
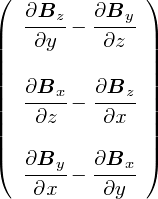
���̃x�N�g���́C�u�R������ԓ��̂ǂ�Ȍ����̉Q�ł��\�����Ƃ��ł���x�N�g���v �ł��D �u�Q��v�������ꍇ�C���̃x�N�g���͂ƂĂ��֗��ȓ���ɂȂ�܂��D �������C���̃x�N�g���������̂́C�Δ����̌v�Z�Ȃ������Ă���̂Ŗʓ|�ł��D ����āC���ʂɂ��̃x�N�g���ɖ��O��t���āC���N�ɕ\�L���悤�E�E�E�Ƃ��������l�����܂����D ���ꂪ�grot�h�Ƃ����L���ł��D
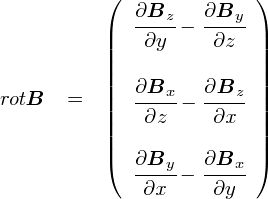
�grot�h�́grotation�h�i���[�e�[�V�����C�u��]�v�j�̗��ł��D �����i������g�������x B �h�ł��j�̑O�ɉ��Z�q�̂悤�Ȋ����ŏ������ƂŁC �u���̏�̒P�ʖʐς�����̉Q�̑傫���v��\�����ƂɂȂ�܂��D rotB�Ə����Ă��܂��ΊȒP�ł����C���̒��g�ł͏�̎��̒ʂ�S�`���S�`���ƕΔ����v�Z�����Ă���킯�ł��D
���āC�������u�x�N�g���̊O�ρv�Ƃ�������v���o���܂��D ����͂��Ƃ��ƁC�u�������x�̒��œd�ׂ���́v��\�����߂ɏo�Ă����b�ł����D �����ł͊ȒP�ɁC�u�~�v�Ƃ����L���̌v�Z�̃��[�������m�F���Ă����܂��D
�ȒP�̂��߁C���̎��ł�x������y�������������x�N�g�� A �ƃx�N�g�� B �ōl���܂��D
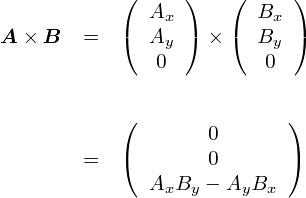
�uA�~B�v��z�������v�Z����ɂ́CA��B��x,y�������g���̂ł����D �i���̂ւ�Ă��Ȍv�Z���@�́C�d�ׂ���͂�\���₷������悤�ɓ����������ߐ��܂ꂽ�̂ł����D�j �|�C���g���ux��y��z��x��y��z... �Ƃ������ԁv�ł��D �O�ς́uz�����v�����߂������́C�uz��x��y�v�̏��Ԃɏ]���āC z�����̊O�ς̑�P�����uAx�EBy�v�ƂȂ�܂��D ��Q���́C�Y�������Ђ�����Ԃ����uAy�EBx�v �ƂȂ�܂��D���Ƃ́u�����Z������v�Ƃ������Ƃ����Y��Ȃ���C�O�ς̌v�Z���@������Ȃ�ËL�ł���Ǝv���܂��D
�ł́C�b��߂��܂��D rot B�̃x�N�g���̊e������ǂ�����ƁC������u�Δ����L���̃x�N�g���i�i�u���ށj�v�Ɓu�������x�̃x�N�g���v�̊O�ςɂȂ��Ă��� ���Ƃ�������܂��D
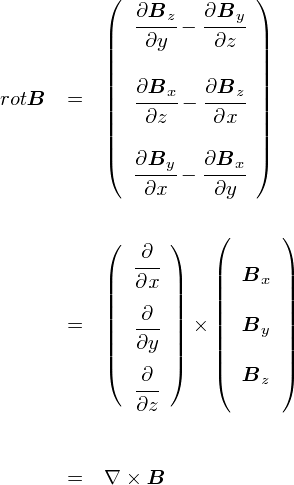
�Ȃ��C�s���悭�������̂��ȁE�E�E�Ǝv���Ƃ���ł��D �����܂Ōv�Z���ꂽ��Łu�ށi�i�u���j�v���l�Ă��ꂽ�̂��͕�����܂��C �i�u���Ƃ����x�N�g���͓d���C�w�Ŕ��ɖ𗧂c�[���ł��ˁD �����Ȃ�������Ȃ������̗ʂ���C�Ɍ���܂��D �i����ŁC���܂�Ɋȗ��������������߂ɁC�����ł͈Ӗ��s���Ȑ����Ɍ�����킯�ł����E�E�E�j
�grot B�h�ƕ\�L����̂��X�}�[�g�őf�G�Ȃ̂ł����C ������u��̓I�Ȍv�Z�̒��g��������v���Ƃ��d�v�����悤�Ǝv���̂ŁC �u�ށ~B�v�̕����g�����Ƃɂ��܂��D �ށ~B�Ƃ����`������������C���[�e�[�V�����̎����ȁE�E�E�Ǝv���Ă��������D
����ł́C�u�}�N�X�E�F����������R���i�����`�j�v�C���Ȃ킿�u�A���y�[���E�}�N�X�E�F���̖@���i�����`�j�v������Ă������Ƃɂ��܂��D �O�Ɍv�Z���Ă������C�u����_�ɂ����鎥�����x B�̐��ϕ��v���v���o���܂��D
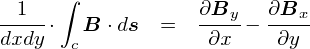
��̎��́C�uxy���ʓ��̉Q�v�Ƃ����ȒP�ȗႩ�瓱�������̂ł����D ���̎�����urot�v�̃C���[�W�����܂�Ă��܂��D �����ŁC���̎����ǂ�ȕ��ʓ��̉Q�ł��Ή��ł���悤�Ɋg�����Ă����܂��D �P�ɁCx,y,z�̂R�������l�����邾���ł��D
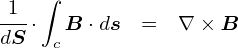
�܂��udxdy�v�̕����́C�����ȖʐςƂ����Ӗ����udS�v�Ə��������܂����D �ǂ�Ȗʂł��ǂ��̂ł����C���̖ʂ̃t�`�ɂ�������]���l���銴���ł��D �܂��C�Δ����̍��͂R�����̃x�N�g���Ƃ������ƂŁC�u�ށ~B�v�ɏ��������Ă���܂��D
���ɁC���ӂ�ʐϕ����܂��D�ϕ�����u�ʁv�́C���R�C�Q�ɉ��������[�v�����ʂł��D �i�P���ɁC���ӂɁudS�v�������Z����C�ƍl���Ă��܂��Ă����܂��܂���D�j
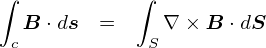
��̎��������Ă��邱�Ƃ́C�u����Q�� B �����[�v�ɉ����Đ��ϕ������l�v�� �urotB�i= �ށ~B�j�����̖ʓ��Ŗʐϕ������l�v�Ɠ������Ƃ������e�ł��D �d�v�Ȃ̂́C���̎��ɂ�����u���ϕ��Ɩʐϕ����ϊ��ł���v�Ƃ����_�ł��D ���̎��͍���̂悤�ɋ�̓I�Ȏ������x�̘b�Ƃ͕ʂɁC �u���ϕ��Ɩʐϕ���ϊ���������v�Ƃ����Ӗ��������Ă��邱�ƂɂȂ�܂��D ���̎����u�X�g�[�N�X�̒藝�v�ƌĂ�Ă����肵�܂��D
�i���u�K�E�X�̒藝�v���̐ϕ��Ɩʐϕ������ւ���̂Ɏg�������ł���̂ɑ��āC ���́u�X�g�[�N�X�̒藝�v�͖ʐϕ��Ɛ��ϕ������ւ�������ł��D ����ŁC�̐ρi�R�����j�C�ʐρi�Q�����j�C���i�P�����j���S�ĂȂ����������ɂȂ�܂����D�j
���̃X�g�[�N�X�̒藝���C���[�W����ۂɂ悭�o�Ă���̂��C���̐}�ł��D
�u�ށ~B�v�Ƃ������́C�u�����ʐς�����̉�]�v��\�����̂ł����D �܂�C�傫�ȃ��\�v�̒��ɂ͊e�n�_���ƂɈႤ�l�����u�ށ~B�v����ʂɂ��邱�ƂɂȂ�܂��D ���̏����ȃ��[�v�����v���Ă���̂��C�X�g�[�N�X�̒藝�̉E�ӂł��D �����ŁC�u���[�v�̓����v�ɒ��ڂ���ƁC�P�P�̔������[�v���d�Ȃ荇���ꏊ�ł� �������݂��ɋt�����ɂȂ��Ă��܂��D ����͎l�p�`�̃��[�v��~���l�߂��}�ɂȂ��Ă��܂����C�~�`�̔������[�v���낤�ƁC �ǂ�Ȍ`�̔������[�v�ł��u�������[�v���d�Ȃ�ꏊ�͉�]���ł��������v���ƂɂȂ�܂��D ����āC���[�v���̑S�ʐςɂ��Ĕ������[�v�����v�������ɁC�Ō�Ɏc��̂��u�t�`�̕��������v �Ƃ������ƂɂȂ�܂��D ���́C�u�t�`�̕����̐��ϕ��v�Ƃ����̂́C�X�g�[�N�X�̒藝�̍��ӂɈ�v���܂��D ���������C����Ȋ����ŃX�g�[�N�X�̒藝�̓C���[�W����Ă���悤�ł��D
�悤�₭�{��́C�u�}�N�X�E�F����������R���i�����`�j�v�ł��D
�������o�Ă����u�X�g�[�N�X�̒藝�v���C���� H �ɂ��ēK�p���܂��D �i�Ƃ͌����Ă��C�O�܂Ŏg���Ă����������x B�Ɋւ��鎮�̗��ӂ���0�Ŋ���Z���������ł��D�j
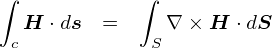
�����ŁC�u�A���y�[���E�}�N�X�E�F���̖@���i�ϕ��`�j�v���v���o���܂��D ���̂悤�Ȏ��ł����D
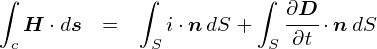
�����ŁC��̂Q���͗����Ƃ��u���� H �̐��ϕ��v�ɂ��Ă̎��ɂȂ��Ă��܂��D ����āC��̂Q���̉E�ӓ��m���Ȃ��Ă݂܂��D
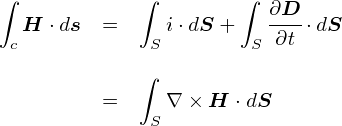
����ƁC���̂悤�ȊW��������܂��D
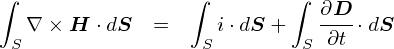
�����ŁC��̎��̂��ׂĂ̍��͖ʐ�dS�Ɋւ���ʐϕ��ƂȂ��Ă��܂��D ���̒��g�i��ϕ����j�̕����������o���āC�������肵�����ɂ��܂��D
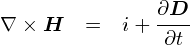
���ꂪ�C�u�}�N�X�E�F���E�A���y�[���̖@���v�̔����`�ł��D
�}�N�X�E�F���������̑�S���ł��D �u�������x�̕ω������[�v��̓d��������v�Ƃ������ł��D
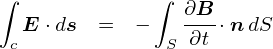
���̑�S���́C���Z�����̓d���C�w�ł����Ȃ��݂́u�t�@���f�[�̖@���v���̂܂�܂ł��D ����̕ω����C�d�������Ƃ����b�ł��D �d�ꂪ�����Ԃ̒��ɂ́C���R�C�d�ʍ����������܂��D�d�ʍ���������C�����ɓd��������܂��D ���ꂪ�������u�U���d���v�ƌĂ���ł��D �܂��C�g�d�ʍ��h���̂��̂ɒ��ڂ��āC�u�������x�̕ω��́g�U���N�d�́h��������v�Ƃ��������������邱�Ƃ�����܂��D
��ɂ���āC��̎��ɂ�����d�� E �⎥�����x B �́u��ԁix�Cy�Cz�j�v�Ɓu���ԁit�j�v�̊��ł��D ���������ƁC�ȉ��̎��ɂȂ�܂��D
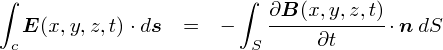
���x�̂��Ƃł����C����(x�Cy�Cz�Ct)�Ƃ�����J�ɏ����Ǝ����S�`���S�`�����Ă��܂��̂ŁC ����͏ȗ����邱�Ƃɂ��܂��D
��������̗���͈ȉ��̂悤�Ȋ����ɂȂ�܂��D������ƏI��点�܂��D
����̎�����u�d�� E�v�ł��D �������C��ԍŏ��ɏo�Ă����}�N�X�E�F���������̑�P���i�K�E�X�̖@���j�ŏo�Ă����d��Ƃ͂�����ƕʕ��ł��D�D�D
�}�N�X�E�F���������̑�P�����u�d�ׁv������d��̘b�ł��D ����ɑ��āC����̑�S���ł��u�������x�̎��ԕω��v������d���ɂ��܂��D ������ɂ��Ă��C�u�d��v�ɂ͕ς��Ȃ��̂ŁC�����ɓd�ׂ�u�����ꍇ�C ���̓d�ׂ͗͂��Ĉړ����܂��D�܂�C�d��������܂��D
�ˑR�C�u�������x�̎��ԕω����d������v�ƌ����Ă��C�s���Ƃ��Ȃ���������܂���D �ǂ����Ă��̑�S���C�u�t�@���f�[�̓d���U���̖@���v�����������Ɏ������̂��C������Ɨ��j�̎����l���Ă݂܂��D
���̖@�������������ȑO�C���Ɂu�d�������������v�Ƃ��������͒m���Ă��܂����D ��R���i�A���y�[���E�}�N�X�E�F���̖@���j�̂��Ƃł��D �Ƃ肠�����C��R���i�ϕ��`�j�̎����o���Ă����܂��D
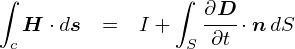
��̎��́C�u�d���C�������͕ψʓd���̎��ԕω������������v�Ƃ����Ӗ��ł����D �����ŁC�d�� I �͑��݂����C�d�����x D �̎��ԕω��݂̂����݂���ꍇ���l���܂��D ���Ƃ��Ắg�d�� I �h�����������ł��D ��̓I�ȃV�`���G�[�V�����Ƃ��ẮC�R���f���T�̋ɔԂȂǂ̃C���[�W�ł��D �g�d���͗���Ă��Ȃ����d��i�d�����x�j�̑傫���͕ω����Ă���h�Ƃ��������ł��D
���ǂ��ł����C��̎����u�d�����x�̎��ԕω��i�ψʓd���j���C����ݏo���v�Ƃ������������Ă��܂��D �����ŁC���̎����u�d��v�Ɓu����v���ɂȂ��Ă��邱�Ƃɒ��ڂ��܂��D �d��i�d�����x�j�̎��ԕω�������ݏo���Ȃ�C���̋t�������Ă͂����̂ł́H �܂�C �u����̎��ԕω��́C�d��ݏo���Ȃ��́H�v�Ǝv���̂́C�f���ȍl�������Ǝv���܂��D
����Ȃ킯�ŁC�u����̕ω����d������v�Ƃ������Ƃ��m���߂邽�߂Ɏ������s���܂����D ���̎����ɂ͎��ƃR�C�����g�����@�C�Q�̃R�C�����g�����@�E�E�E�ȂǂȂǁC �u���Ȃ��݂̃p�^�[���v�����낢��Ƃ���܂��D �Ƃ肠��������́C���̐}�̂悤�ɂQ�̃R�C�����g�����@�ł����܂��D
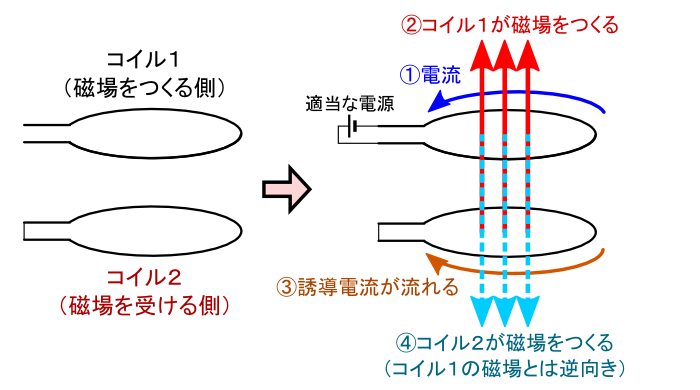
��̐}�̒ʂ�C�ŏ��ɂQ�̃R�C���i�����̉~�`�d���ł����j��p�ӂ��Ă����܂��D �㑤���R�C���P�́C�d���𗬂��Ď���������邽�߂̂��̂ł��D �������R�C���Q�́C�u����̕ω��v���ēd�ꂪ�����邩�ǂ������m�F���邽�߂̂��̂ł��D ������u�R�C���Q�v�̕��ł��D
���̎������ʂ́C���w�Z�⒆�w�Z�̗��Ȏ����ł��Ȃ��݂��Ǝv���܂��D �u�R�C���P�ɓd���𗬂����u�ԂɁC��u�����R�C���Q�ɓd���������v�Ƃ������ʂ������܂��D ���̌��ʂ̉��߂Ƃ��ẮC�ȉ��̗��ꂪ���R���Ǝv���܂��D
�R�C���Q�ɓd���������Ƃ������Ƃ́C���̌o�H�ɉ����ēd�ꂪ�����Ă���؋��ł��D ����āC�u����̕ω����d�������v�Ƃ������������̎����ɂ���Ċm�F�ł��܂��D ���̎��C�R�C���Q�ɐ����Ă���d�����u�U���d���v�iInduced current�j�ƌĂꂽ�肷����̂ł��D ���̗U���d���͊O������������鎥��̕ω��i�R�C���P�̎���̕ω��j���L�����Z����������ɁC��������낤�Ƃ��܂��D
�i���R�C���Q�ɂ́C������ԁi��̎����ł́u���ꂪ������ԁv�j���L�[�v����悤�ɗU���d��������܂��D ����̃P�[�X�Ƃ͋t�ɁC�ŏ��ɏ㑤�̃R�C���P�ɓd��������Ă��Ď���������Ă����Ԃ���C �ˑR�d������Ď�����g���Łh�������Ƃ��܂��D ����ƁC�����̃R�C���Q�ɂ́C����܂ł�����������g�����h����������ɓd��������܂��D ������ɂ��Ă��C�R�C���Ƃ�����ɂ��u����̕ω��������v����������킯�ł��D �d����ON�EOFF�̒���́u���ꂪ�ω�����v���߁C�U���d��������܂��D �������C���̌㎥�ꂪ���̏�Ԃɗ��������Ă��܂��Ɓu����̕ω��v�͖����Ȃ�܂��D ���̎��́C�����U���d���͗���܂���D �j
���́C�u�R�C���ɂ́C�������т������̕ω���W����悤�ɗU���d���������v �Ƃ����@�����u�����c�̖@���v�ƌĂԂ����ł��D �����҂̃����c����iHeinrich Friedrich Emil Lenz�C1804�`1865�j�ɂ��Ȃ��O�ł��D ���̃����c�̖@���́C�d���C�ɂ�����u�����̖@���v�Ƃ��������ł��D
����ł́C����́u�����c�̖@���v�𐔎��ŕ\�����Ƃ��l���Ă݂܂��D ��̓I�ɁC�u����̕ω��̑傫���ɑ��āC�ǂ̂��炢�̑傫���̓d�ꂪ�ł���́H�v �Ƃ������Ƃ�������Ȃ��ƁC���ǂ͎g�����ɂȂ�܂���D�D�D
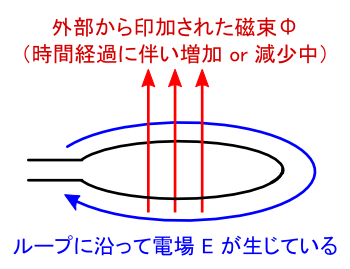
���ǂ��ł����C�g�����c�̖@���h�������Ă��邱�Ƃ́C �u���ԓI�ɕω����鎥���i=�������x B �~�ʐ� S �j��������ꂽ�R�C���ɂ́C ���̎����Ƃ��t�����̎����ݏo���d�� E ��������v�Ƃ������Ƃł��D �����ŁC�u�t�����v�Ƃ����j���A���X�𐔎��ŕ\�����@���l���܂��D
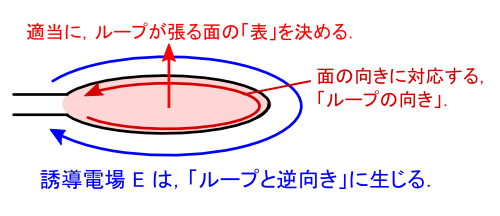
�Ƃ肠�����C�U���d�����l����R�C���ɂ��āC�u���������\���v�Ƃ������������߂Ă��܂��܂��D �����͓K���ō\��Ȃ��̂ł����C��̐}�ł́C�u���̃R�C�����ђʂ��鎥���̌����v�Ɠ����������g�\�h�Ƃ��Ă��܂��D ���̂ق���������₷���C�����܂��D
�����āC��̂��Ƃ��E�l�W�Łu�g�ʂ̕\���h�Ɓg���[�v�̌����h�v��Ή��Â��܂��i���m�ɂ̓x�N�g���̊O�ςł����j�D �E�l�W���āu�l�W���i�ތ����v���g�\�h�ɂ����ꍇ�ɁC���[�v�̐��̌����́u�l�W�������v�ƌ��߂܂��D ���̂悤�Ɍ��߂Ă����ƁC�R�C�����ђʂ��鎥���ɑ��āC�u�t�����̃��[�v�v�Ƃ����̂�������ƌ��߂邱�Ƃ��ł��܂��D
����ŁC�U���d���̌�����������ƒ�܂�܂��D �U���d���͈�����ꂽ������ł����������ɗ����̂ŁC �u�����̌����ɑΉ����郋�[�v�̌����Ƃ͋t�����v �Ƃ������ƂɂȂ�܂��D
����ł́C�K���Ɂu�����c�̖@���v�𐔎��ŕ\���Ă݂܂��D
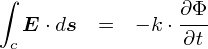
���ӂ��u���[�v�ɉ������d�� E �̑��ʁv��\���`�ƂȂ��Ă��܂��D �g�[�^���łǂ̒��x�̑傫���̓d�� E ��������̂���\�����߂ɁC���ϕ������Ă��܂��D �i���ϕ��̘b���A���y�[���̖@���̎��Ɠ����悤�Ȋ����ł��D�j ���̍��ӂ͈��ʊW�ł����Ƃ���́u���ʁv�ɑ������܂��D
�܂��C�E�ӂ��u���� �� �̎��ԕω��̑傫���v��\���Ă��܂��D �������̎��Ԕ����Ȃ̂ŁC���̂܂�܂ł��D�D�D �����ŁC�}�C�i�X���t���Ă���̂��|�C���g�ł��D ����͂܂��ɁC�u�O������������鎥�����ɑ��āCE ���l���郋�[�v�͋t�����ɐݒ肵�Ȃ����v�Ƃ����C �����c�̖@���̋C���������߂��\���ł��D ���̉E�ӂ͈��ʊW�ł����Ƃ���́u�����v�ɑ������܂��D
��̎��ł́C���������ςɓd�� E ���ł���l�q�����ɂ��������Ȃ̂ŁC ��̓I�Ȓl�̑傫�����u���萔 k �v�Œ������邱�ƂɂȂ�܂��D ���̒萔 k �̒l�������܂�C�u�����̎��ԕω��ƁC��������d��̑傫���v�̊W���������邱�ƂɂȂ�܂��D ����āC���� k �̑傫�������肷�邱�Ƃ͂ƂĂ��d�v�ȍ�ƂƂȂ�܂��D
�i�����Ȃ݂ɁC�萔 k �͖������ʁC�P�ʂ������Ȃ��g�����̐��h�ɂȂ�܂��D ����́C��̎��̗��ӂ̎�������m�F���邱�Ƃ��ł��܂��D ���ӂ͓d��̐��ϕ��ŁC�����Ƃ��Ă��iN/C�Em�j�ł��D ����ɑ��ĉE�ӂ̎����̎��Ԕ����́C�u������ = �������xB�~�ʐ�S�v�C �u�������xB = ��F / �i�d��q �~ ���xv�j�v �ł��邱�Ƃɒ��ӂ���ƁC �݃�/��t = �i�o(N/�iC�Em/s�j�Em2�p/s) = �iN/C�Em�j�ƂȂ�܂��D�萔 k �����������������Ŏ������҂����荇���Ă���̂ŁCk ���͖̂������ʂ��ƕ�����܂��D�j
����ł́C�u�萔 k �v�̒l�ׂ邱�Ƃɂ��܂��D
���̐}�̂悤�ɁC�l�p���R�C��������̒��œ������ꍇ���C���[�W���Ă݂܂��D ����̗�ł́C����̑傫���͏ꏊ���ƂɈقȂ���̂Ƃ��܂��D �E���ɍs���قǁC����͑傫���Ȃ�܂��D
�܂��́C�u�R�C���̕\�ʁv�����߂܂��D ����͎�����������Ȃ̂ŁC�f���ɏ�������u�\�v�Ƃ��܂��D �i�ʂɋt�����ɂ��Ă��C����̋c�_�͒ʗp���܂��D�j ����ɂ���āC���[�v�̐��̌��������܂�܂��D �i�E�l�W�������ł��D�j
����ł́C���̃R�C���������Ƃ����u�R�C���̖ʂ��ђʂ��鎥���v���ǂ��ω����邩���l���Ă����܂��D
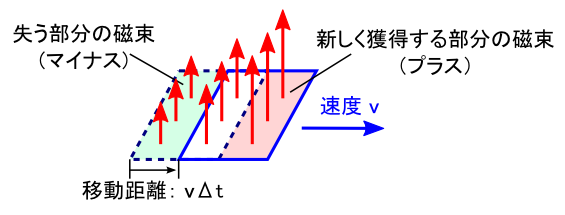
��̐}�ł́C�����O�̃R�C���̈ʒu��j���ŕ\���Ă��܂��D �������瑬�xv�œK���Ȏ��� ��t �����ړ�������̃R�C���������ŏ����Ă��܂��D �����ŁC�ړ��̑O��ŁC�u�R�C���̖ʂ��т������ω��i�����j�v�ɂ��čl���Ă݂܂��D �R�C���͉E���֓����Ă��܂��̂ŁC�R�C���͗ΐF�̕����̎����������Ă��܂��܂��D ���̈���ŁC�ԐF�̕����̎������V���ɓ����Ă���̂ŁC���̕����͑����邱�ƂɂȂ�܂��D ����āC�g�[�^���́g�����̕ω��h�́C
���� = �u�i�ԐF�̕����̎������x�~�ԐF�̖ʐρj - �i�ΐF�̕����̎������x�~�ΐF�̖ʐρj�v
�Ƃ������ƂɂȂ�܂��D ���̒l���S�̂Ƃ��ăv���X�ɂȂ邱�Ƃ�����C�}�C�i�X�ɂȂ邱�Ƃ�����܂��D �v���X�̏ꍇ�̓R�C�����т��������g�����h�������ƂɂȂ�C �}�C�i�X�̏ꍇ�̓R�C�����т��������g�����h�������ƂɂȂ�܂��D�ł́C�u�ΐF�̖ʁv�Ɓu�ԐF�̖ʁv�̋�̓I�Ȗʐς��l���邱�Ƃɂ��܂��D
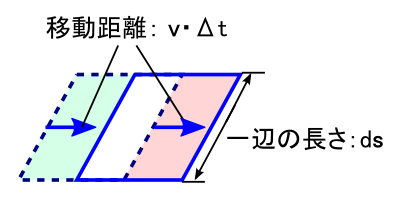
��̐}�̂悤�ɁC�R�C�������x v �Ŏ��� ��t ���������ƁC�����̕ӂƉE���̕ӂ����ꂼ�ꕝ�gv�E�����h �̖ʂ�|���܂��D����ƁC�����`�̃R�C���̂P�ӂ̒������gds�h�Ƃ����ꍇ�C �ԐF�ƗΐF�̖ʂ̖ʐς͋����g�iv�E��t�j�Eds�h�ƕ\�����Ƃ��ł��܂��D �i�ӂ̒������gds�h�Ƃ����L���ŏ����Ă���̂ŁC���Ȃ��݁u�����ȕӂ̒����v�Ƃ����C���[�W�ł��D ����́C��Őϕ��ɂȂ��邽�߂̏����ł��D �Ƃ肠���������ł́C�P�Ȃ鐳���`�̕ӂ̒����Ƃ������ƂŁD�j
�������C�u�ΐF�̖ʁv�Ɓu�ԐF�̖ʁv�ł́C�������J�E���g������@���Ⴄ�̂ł����D �R�C������������̏�Ԃł́C�ΐF�̖ʂ̕����̓R�C���̊O���ɂȂ��Ă��܂��̂ŁC�����������Ă��܂��܂��D ����ɑ��āC�ԐF�̖ʂ̕����̎����̓R�C�����V���Ɋl�����܂��D �܂�C�u�ΐF�̖ʂ̓}�C�i�X�Ƃ��Ď������J�E���g����v���ƂɂȂ�C �u�ԐF�̖ʂ̓v���X�Ƃ��Ď������J�E���g����v���ƂɂȂ�܂��D
�����ŁC�u�ʁv�ɂ��āC���̖ʐς�\���C�u�ʂ̌����v�̏���t��������@�����������Ƃ��v���o���܂��D �u�x�N�g���̊O�ρv�Ƃ�����ł��D �i�O�ς́C���Ƃ��������d�ׂ��������x��������\�����߂ɍ�������̂ł������C ����͂����P�Ȃ鐔�w�I�ȓ���Ƃ��ė��p���܂��D�֗��Ȃ̂ŁD�j
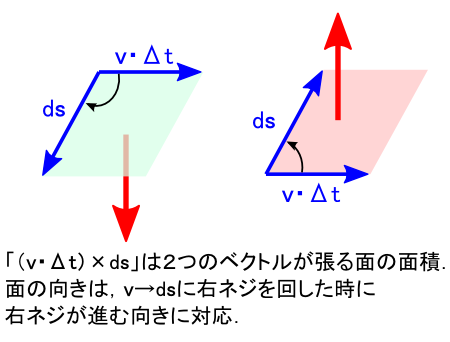
�Ƃ肠�����C�g�iv�E��t�j�~ds�h�Ƃ����O�ς��l���܂��D ���Ȃ��݂ł����C���̊O�ς̑傫���i��Βl�j�� �u�x�N�g�� �gv�E��t�h �ƃx�N�g�� �gds�h ������ʂ̖ʐρv��\���܂��D �܂��C�����Ƃ��Ă� �u�gv�E��t�h����gds�h�Ɍ������ĉE�l�W�������ɁC�E�l�W���i�ތ����v �ƂȂ�܂��D ����ƁC�����g�iv�E��t�j�~ds�h���g���C ����́u�̖ʂ̓}�C�i�X�i�������j�v�C�u�Ԃ̖ʂ̓v���X�i������j�v�Ƃ����b�����ꂢ�ɕ\���邱�Ƃ�������܂��D
���ǂ��ł����C�gds�h�̌����́C��ԍŏ��Ɍ��߂��u�R�C���̃��[�v�̐��̌����v�ɂƂ��Ă���܂��D �gds�h�̌����̓��[�v���̊e�ӂ��ƂɈقȂ�̂ŁC �g�iv�E��t�j�~ds�h�̌������ꏊ���Ƃɕς��E�E�E�Ƃ����̂��~�\�ł��D
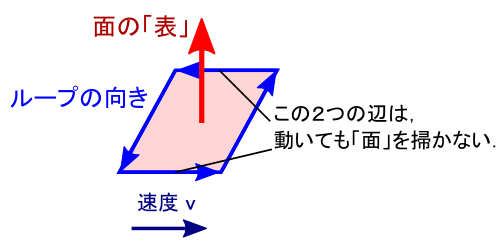
���Ȃ݂ɁC���[�v�̒��ŁC��̐}�̏㑤�̕ӂƉ����̕ӂ́gds�h�̌����� ���x v �ƕ��s�ɂȂ��Ă��܂��D ���̂��߁C�g�iv�E��t�j�~ds�h�̒l�̓[���ɂȂ�܂��i |A�~B| = A�EB�Esin�ƁC�Ƃ�A��B���Ȃ��p�j�D ���́u�O�ς̒l���[���v�Ƃ����v�Z���ʂ́C�R�C���������C���[�W������ƁC �u�㑤�Ɖ����̕ӂ͓����Ă��ʂ�|���Ȃ��v�Ƃ����C���[�W�ƈ�v���܂��D
�ȏ�̘b���܂Ƃ߂�ƁC�R�C�������������Ɋe�ӂ��|���ʐς́C�������܂߂� �g �iv�E��t�j �~ ds �h�ŕ\�����Ƃ��ł���E�E�E�Ƃ��������ɂȂ�܂��D
�����܂ł̘b����C �u�R�C�����ђʂ��鎥���̕ω��v�́C�v���X�E�}�C�i�X�S���܂߂āC���̎��ŕ\�����Ƃ��ł��܂��D
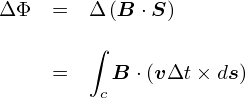
���ϕ��̌`�ɂȂ��Ă���̂́C��̂��Ƃ��C�ϕ��o�H�i���[�v�j��������ƈ�����Ă��������E�E�E�Ƃ����Ӗ��ɂȂ�܂��D ���̐ϕ��o�H�̓R�C���̊e�ӂƂ������ƂɂȂ�܂��D ��̕ӁC���̕ӁC���̕ӁC�E�̕ӁE�E�E�ƁC�e�ӂ��ƂɁg�iv�E��t�j �~ ds �h ���v�Z���āC�S���o���Z���܂��D ����Ŋe�ӂ��|���u�ʁv���C���������݂ōl���Ă��邱�ƂɂȂ�܂��D �܂��C�������x B �́C�e�n�_�ɂ����� B �̒l���g���܂��i�������x B �͏ꏊ�̊��Ȃ̂Łj�D
���āC���������g�萔 k �h�����肷�邽�߂Ɏ����������ƂɂȂ�܂��D
�܂��C��ϕ����ł��� �g B�E�iv��t �~ ds�j�h�̕������u���ρv��u�O�ρv�̎菇�ɏ]���ăo�����܂��D
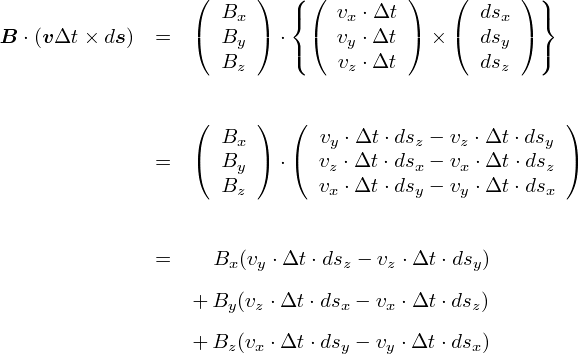
����ɁC�o�����I�������̐������č\�z���܂��D ���̎��C�ŏ��̎��Ƃ͈Ⴂ�C�g ds �h�ł�����`�ɂ����Ă����܂��D
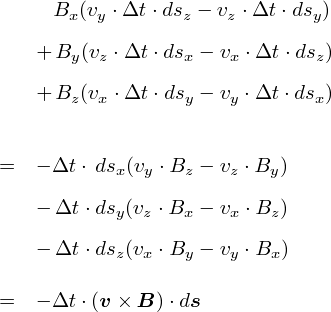
�gds�h������`�ɕό`����ƁC�����ꂽ�g�iv �~ B�j�h�Ƃ����`���o�Ă��܂����D �ł͉��߂āC���ό`�����������̎��ɖ߂��܂��D
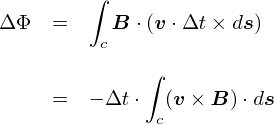
�S�`���S�`���ƕό`�����܂������C ���Ǐ�̎��������Ă���̂́u�R�C�������������̎����̕ω��v�Ƃ������Ƃł��D
����ł́C�����c�̖@���ɏo�Ă����u�������x�̎��ԕω��v�����ŕ\���܂��D �P�ɁC��̎������ԂŔ������邾���ł��D
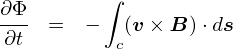
�ł́C���߂āg�萔 k �h���g���ēK���ɂ��܂����Ă����u�����c�̖@���v�̎����o���Ă����܂��D
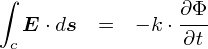
���ǂ��ł����C��̎��́u�����̎��ԕω����C���[�v��̓d������v�Ƃ����Ӗ��ł����D ���̉E�ӂ̕����ɁC���܂܂ō����d��/dt�̎��������Ă��܂��܂��D
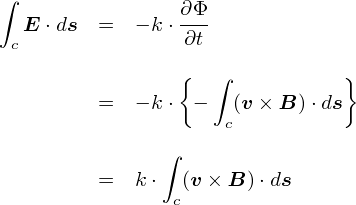
��̎��ł́C���ӂƂ��������[�v�i�R�C���̃��[�v�j�ɉ��������ϕ��ɂȂ��Ă��܂��D ���ꂪ���ӂň�v���Ă��邻���Ȃ̂ŁC �ϕ��̒��g�������Ђ��ς�o���Ă��܂��܂��D
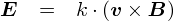
����ƁC���Ȃ��݁u�d�� E �v�ƁC�u���x v �~ �������x B �v�Ƃ̊W�����o�Ă��܂����D
���Ƃ��ƁC�d�� E �⎥�����x B �Ƃ�����́C�u�d�ׂ���� F �v��\�����߂ɍ��ꂽ�̂ł����D
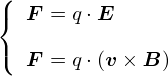
����́u�R�C�����������x�̒��œ������v�Ƃ��������ł́C �R�C���ɓd��������܂��D �d���������Ƃ������Ƃ́C�d�ׂ��͂��ē�������Ă���킯�ł��D ���̌����́C�u�d�ׂ��d�� E ����� F ���Ă��邩��v�ƃC���[�W���邱�Ƃ��ł���C �u�d�ׂ��������x B ����͂��Ă��邩��v�ƍl���邱�Ƃ��ł��܂��D �i�������́C���[�����c�̘͂b�ɂȂ�܂����D�j
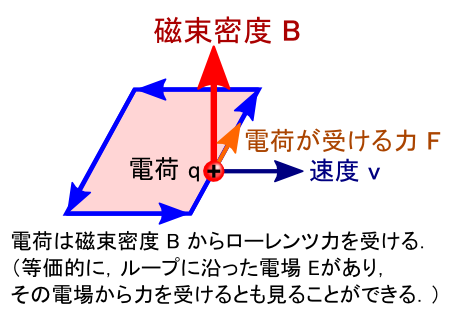
���Ȃ݂ɁC����̂悤�Ɂu�ꏊ�ɂ���Ď������x B ���Ⴄ�v�Ƃ����ꍇ�C �e�ӂɐ����郍�[�����c�͂̑傫�����o���o���ł��D ���̂��߁C���[�v�S�̂Ƃ��Ă݂�ƁC�d�ׂ̓����͈�����ɕ邱�ƂɂȂ�܂��D ���ꂪ�u���[�v�ɉ����ēd���������v�Ƃ������ʂɂȂ���܂��D
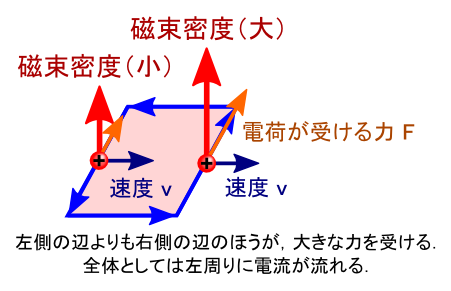
���āC�d�ׂ���� F �́u�d�� E ����̗͂��v�ƍl���悤�ƁC �u�������x B ����̗͂��v�ƍl���悤�ƁC �����P�̓d�ׂɒ��ڂ��Ă���b�Ȃ̂ŁC���R�CF �̒l������łȂ�������܂���D
����āC
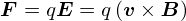
�ƂȂ�͂��ł��D ����ƁC�������o�Ă����g E = k�E�iv�~B�j�h�Ƃ������́C
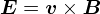
�ƁC�g k =1 �h�ƂȂ�K�v�����邱�Ƃ�������܂��D �悤�₭ k �̒l�����܂�܂����D�D�D
���߂āC�ŏ��̎��� k = 1 �������Ă݂܂��D
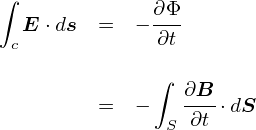
����Ȃ���ȂŁC�u���[�v���̎������ω������ꍇ�C�����ɐ�����d��v�̎����������܂����D ������u�t�@���f�[�̓d���U���̖@���v�iFaraday's law of induction�j�ƌĂ�Ă��܂��D �t�@���f�[����iMichael Faraday, 1791�`1867�j�Ƃ����l�����������̂ŁC ����ɂ��Ȃ��O�ł��D
�}�N�X�E�F���������̑�S���C �t�@���f�[�̖@���́u�����`�v�ł��D �u�������x�̕ω����Q��̓d�������v �Ƃ����b�ł��D
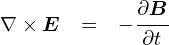
�u�t�@���f�[�̖@���v���̘̂b�́C���� ��S���F�t�@���f�[�̓d���U���̖@���i�ϕ��`�j�̂Ƃ���ōς܂��Ă���܂��D ����́C�ϕ��`�̂Ƃ���ō���������u�����`�v�ɕό`�����Ƃ����ł��D
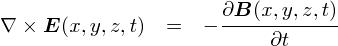
��ɂ���āC�d�� E �⎥�����x B �͎��� t �Əꏊ (x, y, z)�̊��ł��C ���J�ɏ����Ə�̂悤�ɂȂ�܂����C����͏ȗ����܂��D
����͂�������ł��D�grot�h�������o���āC�����`�̎����d�グ�܂��D
�����I�ȓ��e�ŁC�V�����l�����Ƃ͓��ɂ���܂���D�D�D �������S�`���S�`���Ƃ����邱�Ƃɂ��܂��D
�܂��C�ϕ��`�ŏo�Ă����u���[�v�ɉ����� �d�� E �̐��ϕ��v���C �X�g�[�N�X�̒藝���g���ĕό`���܂��D
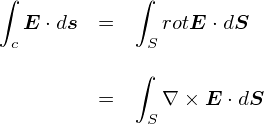
�܂��C�u���� �� �v�Ƃ�����́C�u�������x B �~ �ʐ� S�v�ŋ��߂�ʂł����D ��̂��Ƃ��C�ꏊ���ƂɎ������x B ���قȂ�ꍇ�ɑΉ����邽�߂� �ʐϕ��̌`�ŏ����Ă����܂��D
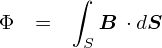
�����܂ł̘b���u�t�@���f�[�̖@���i�ϕ��`�j�v�ɑ������ƁC���̂悤�ɂȂ�܂��D
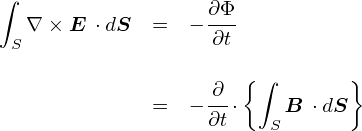
�����ŁC���[�v�ň͂�ꂽ�u�ʐρv�͎��Ԃɂ�炸���ƍl����̂ŁC ���Ԕ����̍��� dB/dt �����ɂȂ�܂��D
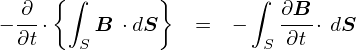
������C���Ƃ��Ƃ̎��ɑ������ƁC���̂悤�ɂȂ�܂��D
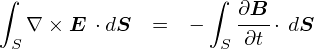
�����Ƃ������ʐ� S �Ɋւ���ϕ��Ȃ̂ŁC ��ϕ������������o���Ă��܂��܂��D
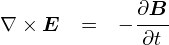
��̎����C�u�t�@���f�[�̖@���i�����`�j�v�ł��D
�ȏ�ŁC�S���I���ł��D �����l�ł����D�D�D