トップページ > フーリエ変換入門(FFT入門) > オイラーの定理(5)
【遊び方】
スライドバーを動かすと,水色の点が動きます。
黒い画面部分をドラッグすると視点が動きます。
※エラーになった場合,再読み込みすると表示されることが多いようです。
Java3Dをインストールしないと下のアプレットは表示されません。お手数ですが,
Java3Dインストール方法
の手順に従ってJava3Dをインストールしてください。不便なので,近々Flashに置き換えます。
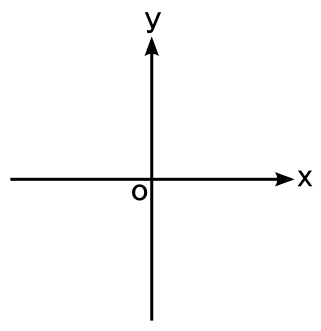
一般的に「座標」と言えば, x軸 と y軸があるアレをイメージすることが多いと思います。 そもそもこれは,「 x と y は完全に独立だから,それぞれの値のいろいろな組み合わせを平面に書けば分かりやすい」 からです。そんなわけで「グラフ」として x-y 間の関係を表現するのが多く用いられています。

これと同じノリで,「複素数」を2次元のグラフに表現することを考えてみます。 複素数は「 a + jb」のような感じで,ただの定数 a の「実部」と,jがついている jb の部分である「虚部」の 2つから成っています。実部と虚部は絶対に混じることはなく,「独立」となっています。 そんなわけで,座標の横軸を実数用の「実軸」,縦軸を虚数用の「虚軸」としてみます。
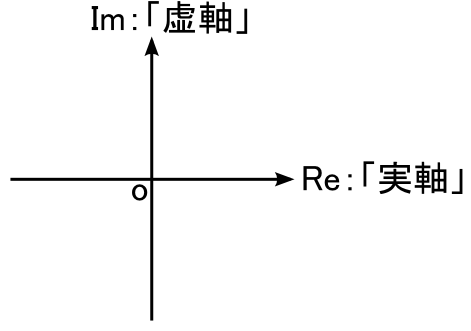
“Re”というのは Real Part (実部)の略,“Im”というのは Imaginary Part (虚部)の略です。 この「複素数平面」で,前ページで作ったオイラーの公式を表現することを考えます。 オイラーの公式は次のような感じでした。
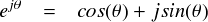
これを複素平面上でプロットしてみます。「 ejθ 」のままではどうしようもないので,早速オイラーの公式を使って,実部にcos(θ),虚部にsin(θ)としてプロットします。次のような感じになります。
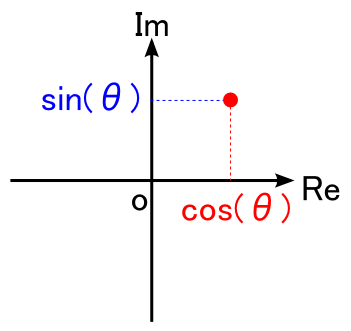
これは高校数学でおなじみの,「単位円」の図にそっくりです。。。
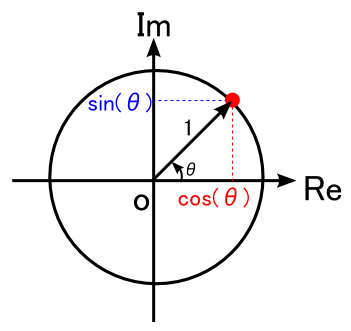
そんなわけで,オイラーの公式が言ってる事は,「 ejθ というのは 複素平面で単位円の上を移動する点を表している 」・・・ということになります。
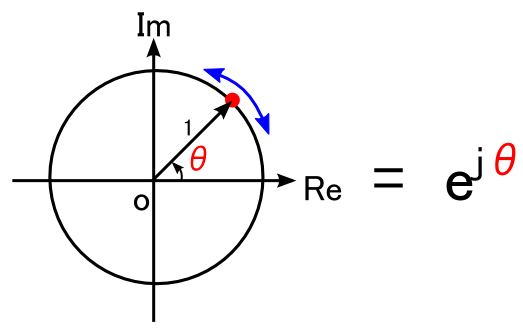
また,別の見方として「点」ではなく,「複素平面上で原点から単位円上の1点へ伸びているベクトル」として ejθを考えることもできます。 時計の針のようにグルグル回転するベクトルというイメージになります。 このイメージから, ejθ のことを「複素ベクトル」と呼ぶ場合もあります。
ここまでは, ejθのイメージを作るために,2次元平面上の円をイメージしました。 しかし,オイラーの公式「 ejθ = cos(θ) + jsin(θ) 」では, 実軸に「cos(θ)」,虚軸に「sin(θ)」,それら2つのパラメータである「θ」と,3つの変化する量が関わっています。 そんなわけで,本当の(?)イメージを得るには軸を3本用意する必要があります。すなわち,3次元のグラフを書くことになります。
・・・というわけで作ったのが冒頭のアプレットです。 θの値が増加すると,水色の点(これが ejθ の値に対応)がぐるぐると動きます。 ただし,θ軸上での移動もあるので結局「らせん」を描くことになります。
とりあえず,グルグル動かして遊んでいただければ良いのですが,確認しておきたいポイントを2つ紹介します。 まず,「 ejθ の実部が本当に cos関数 になっているのか」ということを見てみます。 これを確認するには,うまく視点を動かして「横軸がθ軸,縦軸がRe軸(実軸)」になるようにします。 3Dプロットなのでらせんっぽい感じが残っていますが,下図のように原点付近ではちゃんと cos関数 の形になっています。
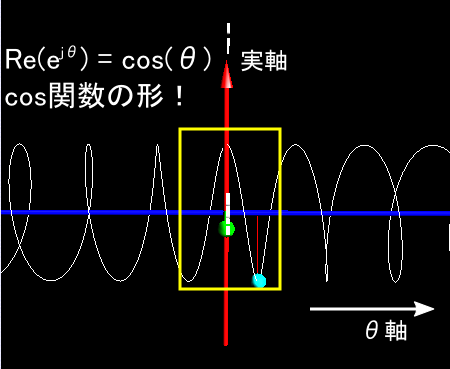
同様に,「 ejθ の虚部が sin関数 になっている」ことを確認します。 視点を動かして,「横軸がθ軸,縦軸がIm軸(虚軸)」になるようにします。 するとやはり,原点付近でしかきれいな形になりませんが,確かに sin関数 になっています。
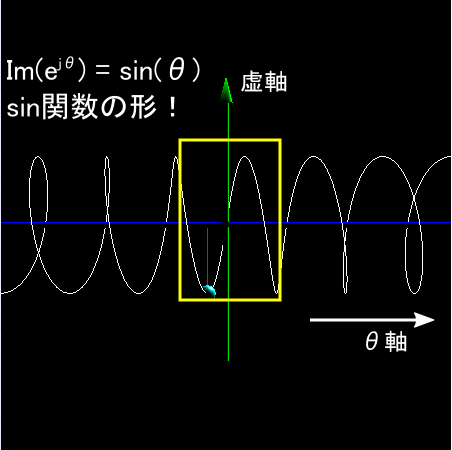
以上から, ejθは複素平面で表すと円上をグルグル回る点であること, 3次元のグラフを書けば,らせん状の動きをする点でcosとsinを同時に表していること・・・が確認できました。 しかし,「複素数だから,あまりしっくりこない・・・」と思われてしまうかもしれません。 とりあえず,フーリエ解析においては,簡単に「 ejθ はsin関数とcos関数を同時に表せる便利なもの」 程度のイメージで十分だと思います。
フーリエ級数のところでは,様々な波形をsinとcosを組み合わせて表現していました。 もし「 ejθ」を使えば,複素数とはいえ sin と cos が両方含まれているので, フーリエ級数をもっと簡潔に表すことができます。 また,「複素ベクトル」とはいえ, ejθは「指数関数」であることには違いありません。 フーリエ解析では微分や積分がやたら出てきますが,指数関数では微積分の操作が非常に簡単です。 これが ejθを導入する利益という感じになっています。