トップページ > フーリエ変換入門(FFT入門) > オイラーの公式(4)
前ページでは,sin関数とcos関数のテイラー級数展開を確認しました。 前回に引き続き,もう1つだけテイラー展開をやっておきます。 指数関数:ex のテイラー展開です。
まず,テイラー展開可能かの判定をします。くどいですが,剰余項は次式で表わされるのでした。
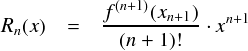
今回の相手は指数関数なので,上式の f(x) は ex ということになります。 当然,何階微分しても形はかわりません。なので,剰余項に代入すると次のようになります。
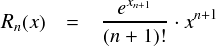
ここで,e の指数となっている xn+1 は適当な定数です。コーシーの平均値の定理で出てきた条件を満たしている感じです。 この Rn(x) の収束判定ですが,前ページでsin・cos関数でやったのと同様に ,数列と見て比をとる方法でやってみます。
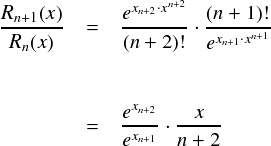
上式の中では,n以外は全て定数と見れるので,結局 n → ∞ の極限はゼロになります。
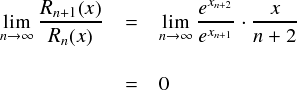
以上から,「指数関数 ex はテイラー展開可能」 だと確認できました。
そんなわけで,指数関数をテイラー展開していきます。指数関数は何階微分しても同じ形なので, 係数を求める作業も簡単に済みます。。。
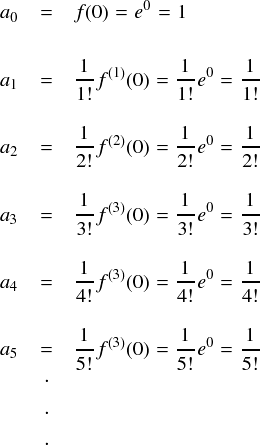
係数を一般化すると,次式のようになります。三角関数と違って,符号が常に正で飛ばす項もありません。 けっこう分かりやすい形に展開できます。
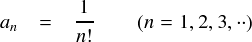
以上をまとめて,指数関数のテイラー展開は以下のようになります。規則性があって,それっぽい感じです。
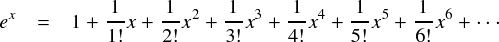
あまりパッとしなかったので,グラフは出さないことにします(ぇ
前ページで作ったsinとcosのテイラー級数ですが,この2つの級数はなんとなくexのテイラー級数と噛みあいそうな(?)感じがします。
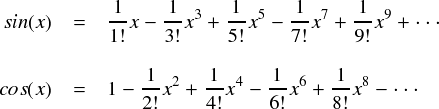
係数の数字は同じなので,問題なのは符号です。符号を揃えるために,虚数を使ってみます。
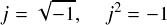
ここで,「 j 」は「虚数単位」と呼ばれるやつです。高校数学では「 i 」と表記すると習っていました。 しかし,今後は虚数単位として「 j 」を使います。 電気屋さんの間ではおなじみかと思いますが,電気系の学科では虚数は必ず j を使います。 理由は 「i という文字が既に電流を表す文字として割り当てられているから」です。 きっと,電気屋さんにとって電流は何よりも大事なんだと思います。。。
そんなわけで,ex の変数を x から 「 jx 」にしてみます。
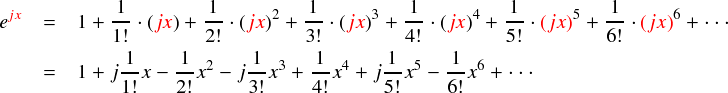
上式を,実部と虚部を分けるように書きなおしてみます。
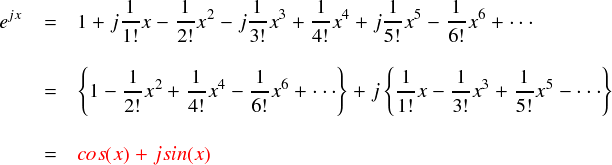
・・・ということで,上式で実部・虚部でくくった時にでてきた項は,cos関数・sin関数のテイラー級数と全く同じ形になっていました。以上から,指数関数とsin関数・cos関数を結びつける「オイラーの公式」できました。 変数は x のままでも良いのですが,sinやcosの変数といえば「角度:θ」が定番なので, ここでも変数をθにしておきます。
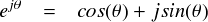
この ejθ は,sinとcosを同時に表せて便利な道具という感じになります。 その他にも,さまざまな物理現象を表現するのに都合が良いものとなっています。 とりあえず,次ページではこれをどう解釈しておけばよいのかという話になります。