トップページ > フーリエ変換入門(FFT入門) > オイラーの公式(3)
まずは,sin 関数を多項式の形で表せるのかを確認してみます。 前ページで出てきた「剰余項」は,次のような形でした。
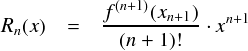
これから,この Rn の極限を調べることになります。 もし n → ∞ の極限でこの Rn がゼロになれば,sin関数はテイラー展開可能ということになります。 今回の f(x) は sin(x) です。sin 関数は何度微分しても sin と cos を行ったり来たりするだけで,かつ, その絶対値は必ず 1 以下に収まっています。よって,極限を調べるだけなら, 単に「 f(x) = 1 」としてしまって,上から抑え込んでおいたほうが楽です。
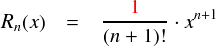
とりあえず,これの収束性を調べるには,数列的な見方で片付けるのが分かりやすいかと思ったので,次のような数列を用意してみます。
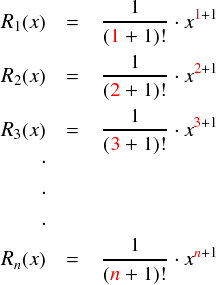
ここで,an と an+1 の比をとってみます。
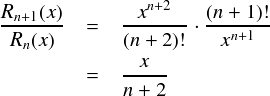
上式で n → ∞ の極限を取ると有限値の分子に対して分母が無限大となるので,
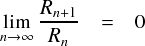
以上のことから,sin関数の剰余項は n に対して減少し,最後はゼロになることがわかります。 よってsin関数はテイラー展開可能だということが分かりました。
それでは,sin関数をテイラー展開したときの各係数を求めていきます。 多項式関数のところで作っていた各係数を求める公式は次のようなものでした。
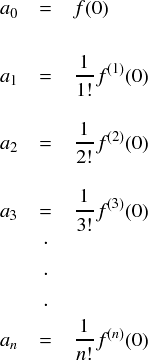
sin 関数の場合,微分するごとに sin(x),cos(x),-sin(x),-cos(x) となり,4階微分以降は再び sin(x) から繰り返し同じ形が続きます。また,sin(0) = 0 であることに注意すると, sin(x) をテイラー展開するときの係数は次のような感じになってます。
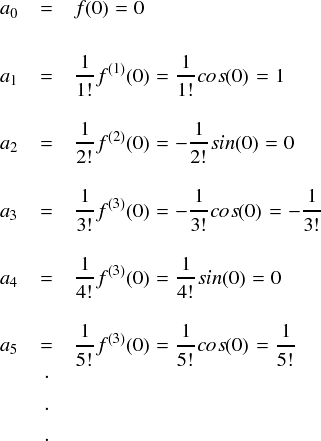
sin(0) が入るところは全てゼロになって消えてしまうので,残るのは1,3,5・・・と奇数番目の項だけということになります。そして,その係数は正・負が交互に現れて,分母に階乗が入る・・・という形です。 なんだか規則性があって,それっぽい感じがします。 せっかく規則性があるので,一般化してきれにまとめてみます。。。
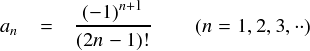
よって,sin関数のテイラー展開は次のようになります。
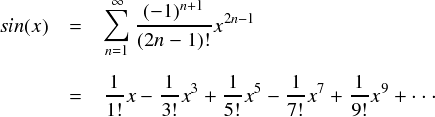
sin関数のテイラー展開は,奇数項のみが残る形となりました。また,その項の次数と係数の階乗の値とが対応してます。 これであの滑らかな sin関数が再現できるというのも不思議な感じです。。。
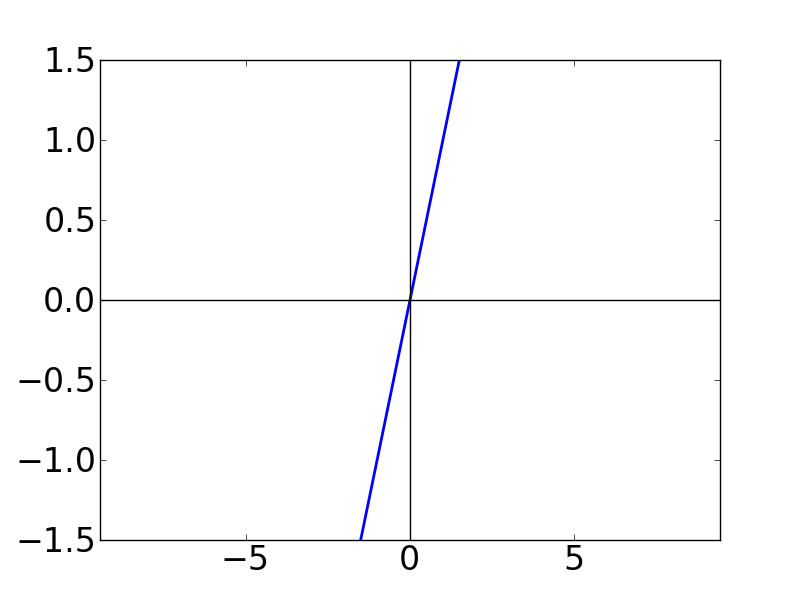
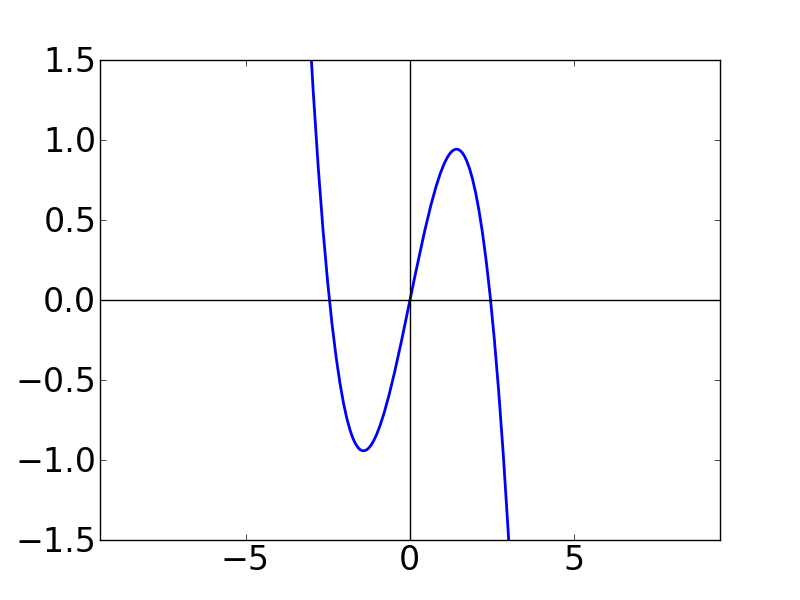
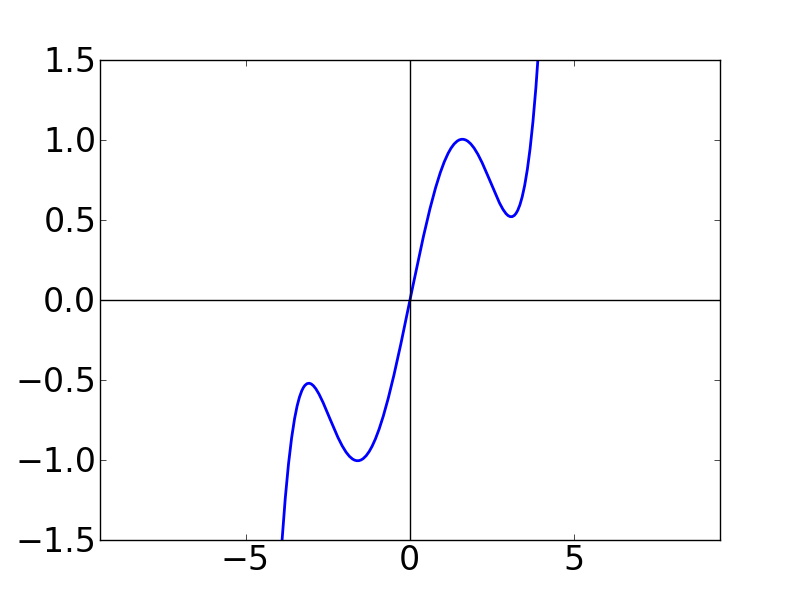
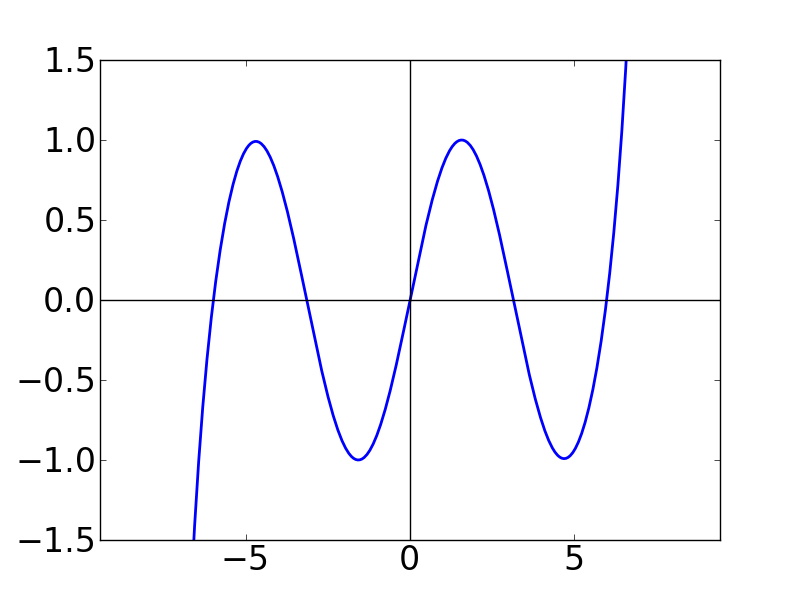
上で求めたsin関数のテイラー級数について,第 N 項までの和についてグラフを書いてみます。
| N=1 | N=2 | N=3 |
 |
 |
 |
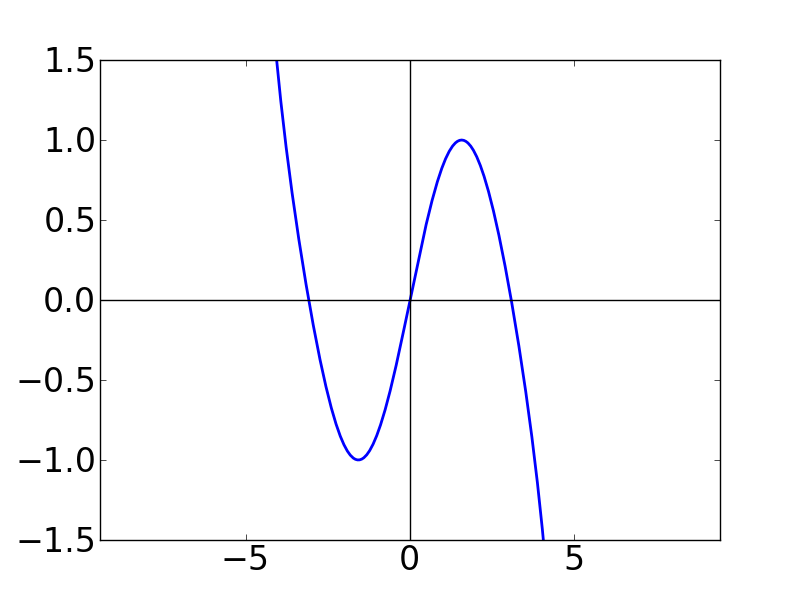
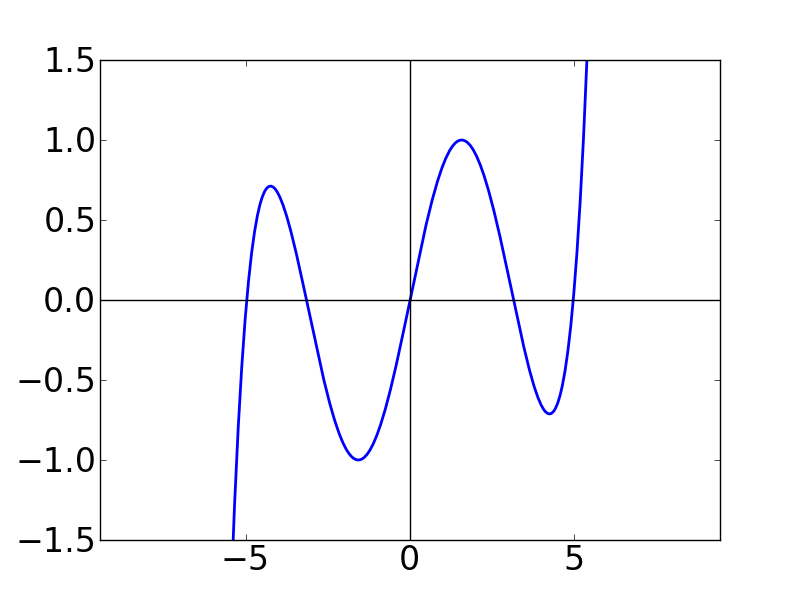
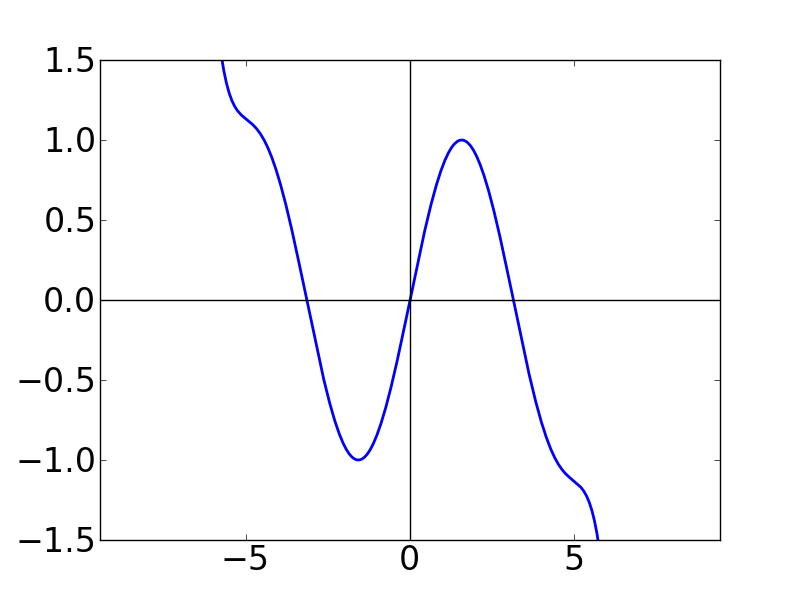
| N=4 | N=5 | N=6 |
 |
 |
 |
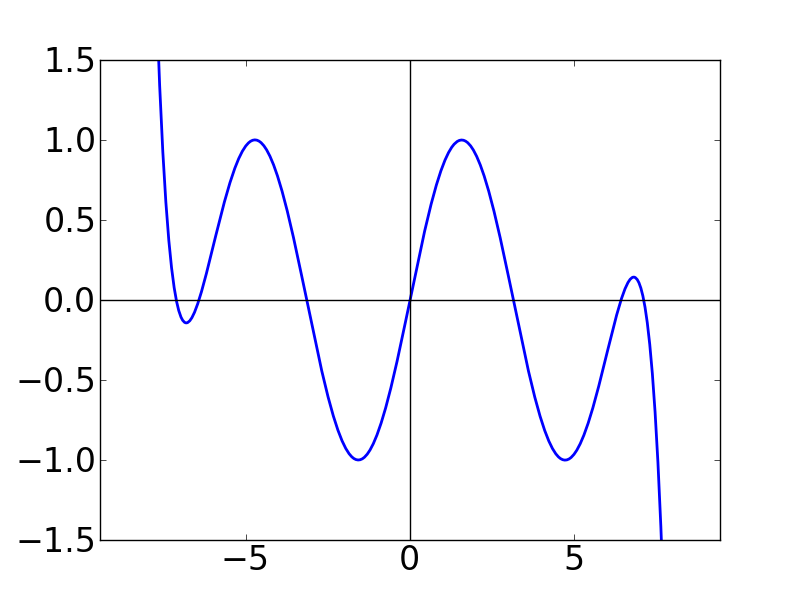
| N=7 | N=8 | N=9 |
 |
 |
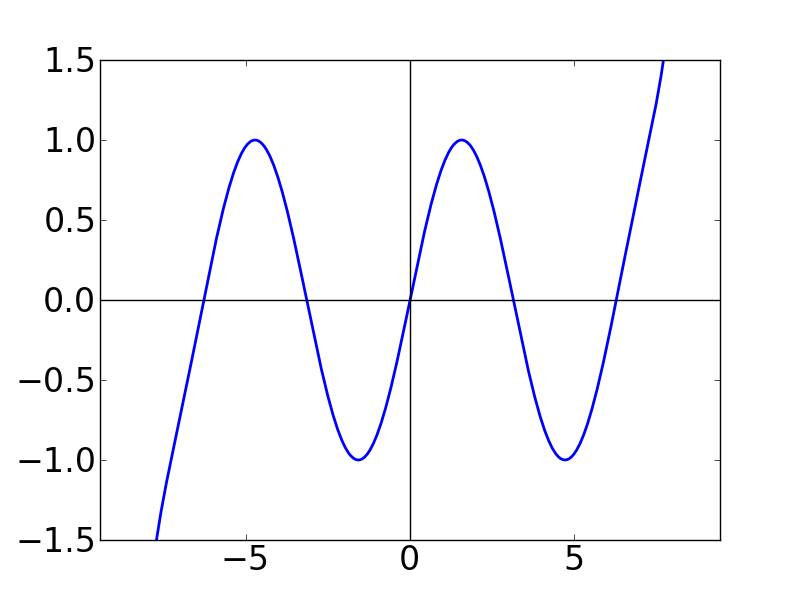 |
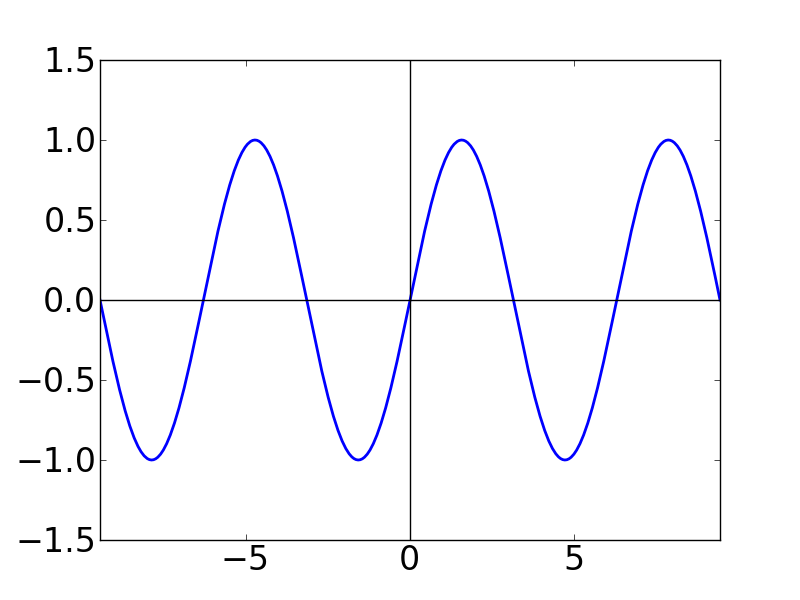
N の値が大きくなると,テイラー級数がどんどん sin 関数に巻きついていく(?) ことが分かります。 N = 50 として書いたグラフが下図です。こうなると, もはや sin 関数に見劣りしません。 N → ∞ とすれば,確かに多項式関数でも sin関数と一致する気がします。 不思議ですね。。。
| N=50 |
 |
次は,sin関数と同じノリで cos関数のテイラー展開もやってしまいます。 剰余項の扱いは,結局sinでもcosでもRn(x) の分子が 1 以下ということで共通なので, sin関数の時と同じ流れでcos関数もテイラー展開可能であることが示せます。
各項の係数を求めると,次のような感じになってます。
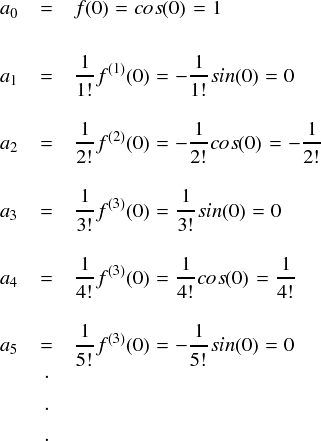
・・・という感じで各項ごとの係数が求まります。 これを一般化すると次式のようになります。
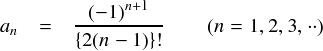
以上から,cos関数のテイラー級数展開は次式となります。
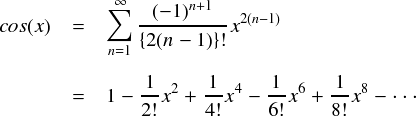
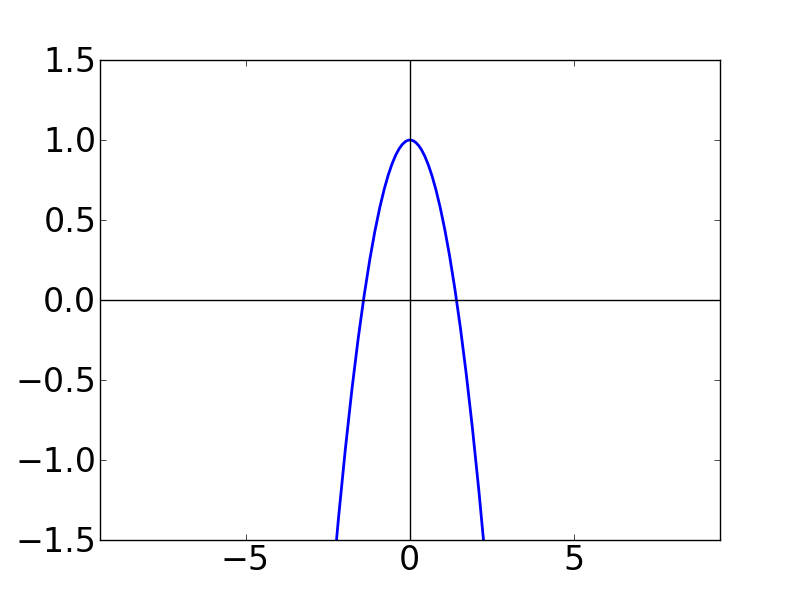
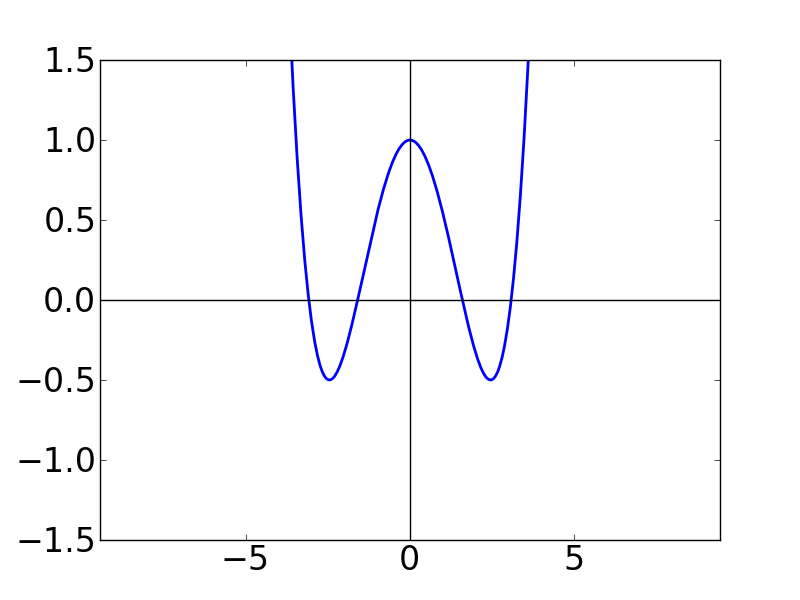
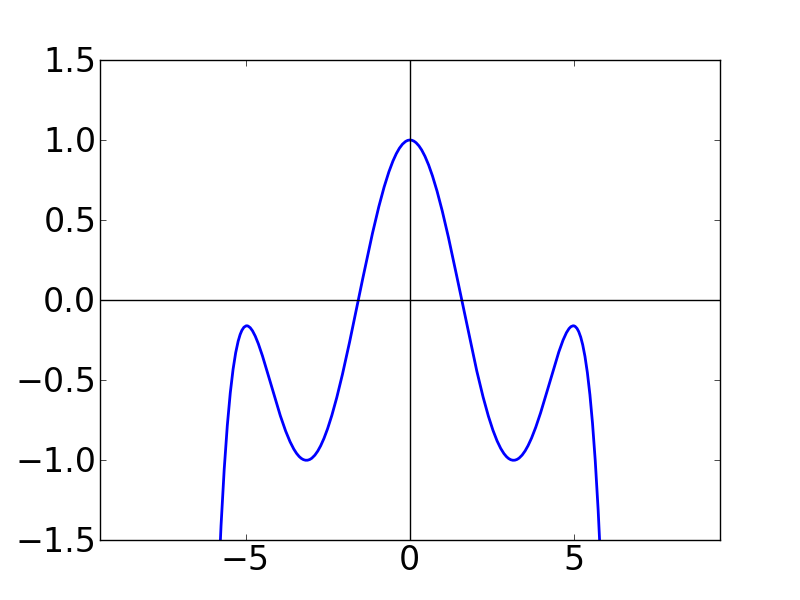
例の如く,cos関数のテイラー級数について,第 N 項までの和のグラフを書いてみます。
| N=1 | N=2 | N=3 |
 |
 |
 |
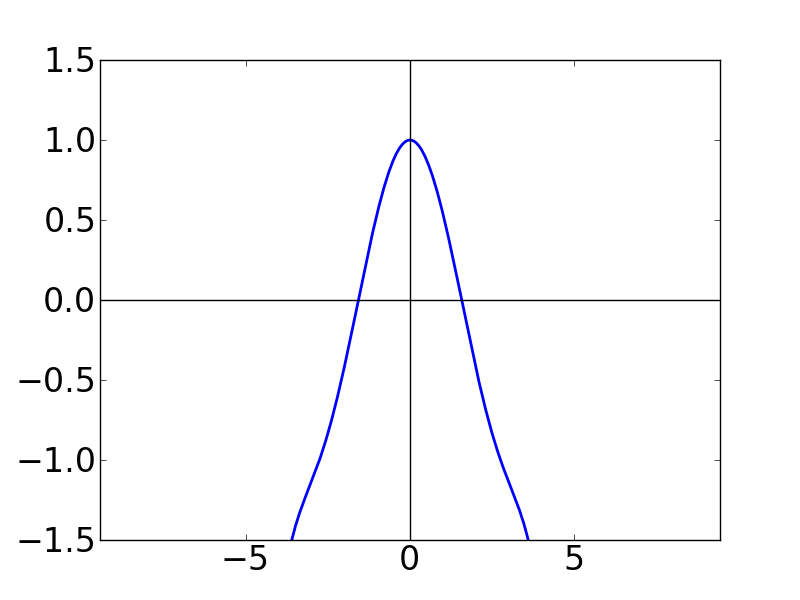
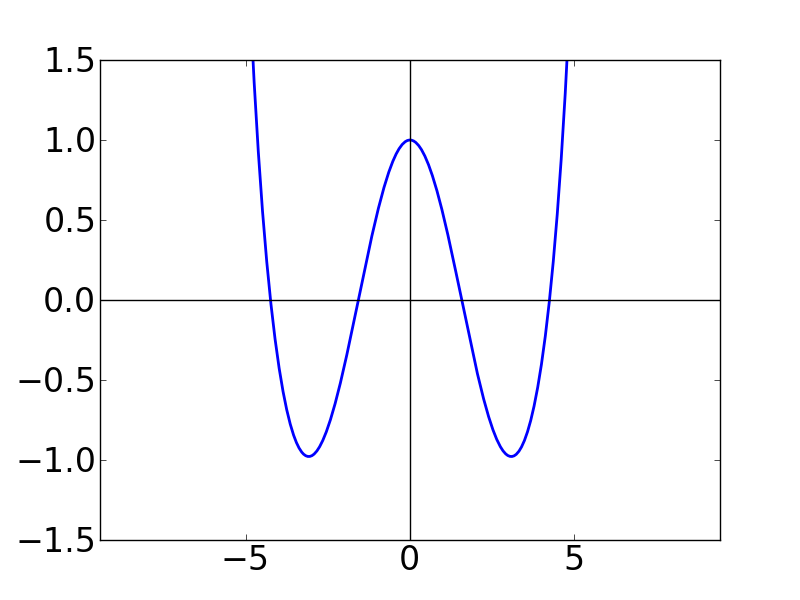
| N=4 | N=5 | N=6 |
 |
 |
 |
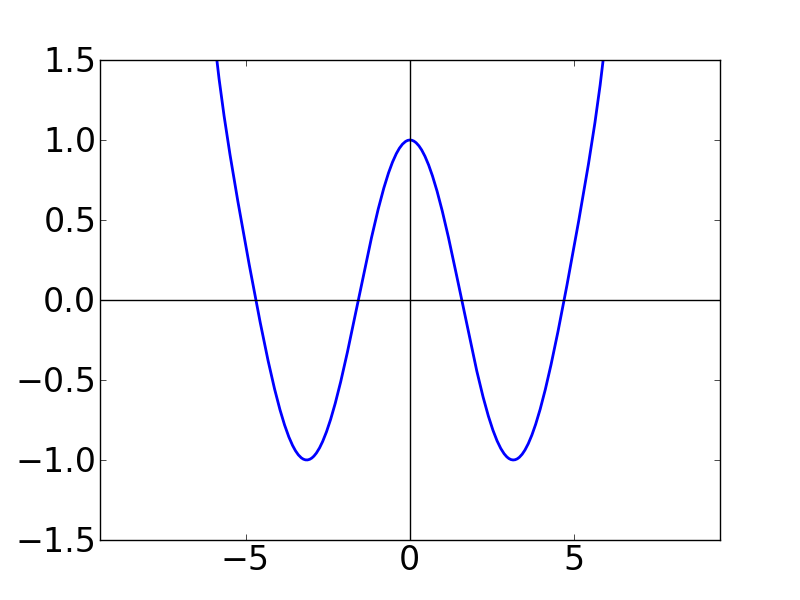
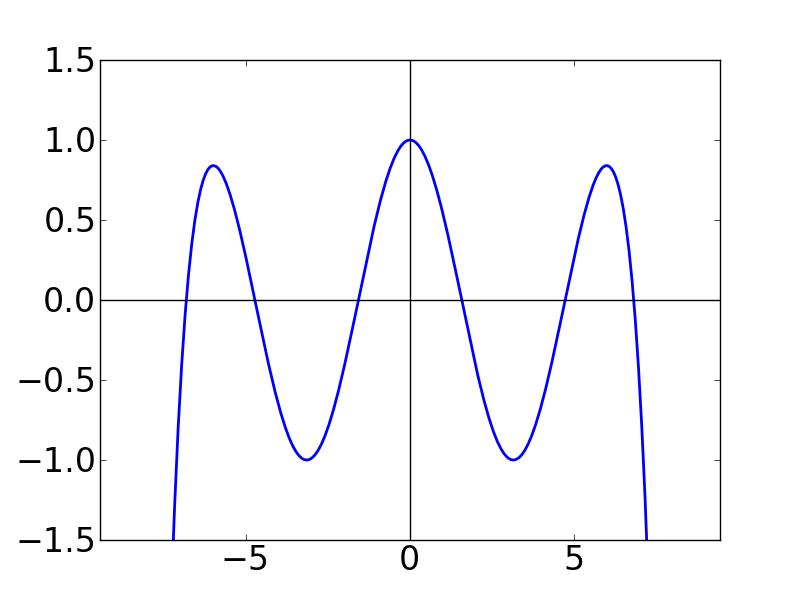
| N=7 | N=8 | N=9 |
 |
 |
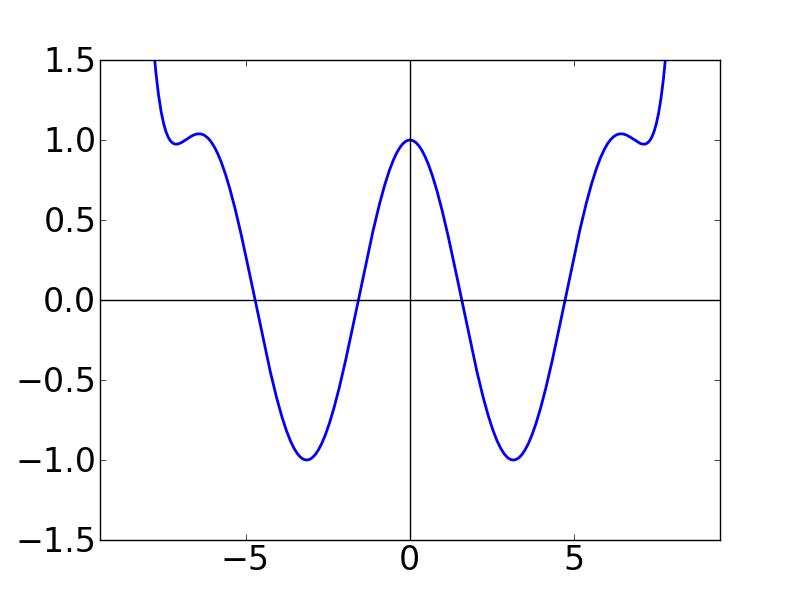 |
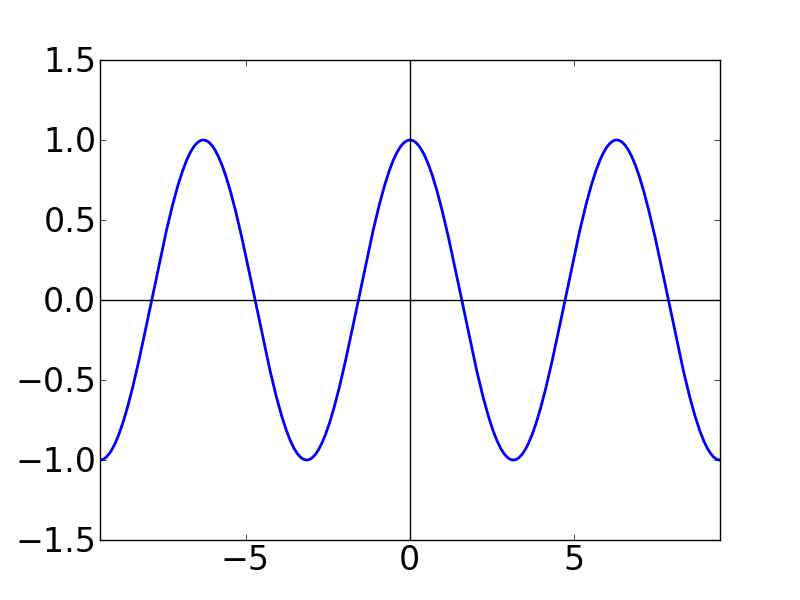
N = 50 の時のグラフが下図です。もはや cos関数になってます・・・。
| N=50 |
 |
以上で,必要な道具はほとんど揃いました。 次ページでは最終目標の「オイラーの公式」を作ります。。。
このページでは,sin関数やcos関数が多項式関数として表わせることを確認しました。 ・・・ということは,足し算・引き算・かけ算・割り算さえ可能であれば,完全に三角関数を再現することができるということです。
とはいえ,どうしても数学の抽象的な話はにわかに実感しづらいところがあります。 そんなわけで,sin関数をテイラー展開 (x方向にズラしてない普通の(?) sin関数なので,いわゆる「マクローリン展開」なんですけど,)を計算するディジタル回路を作ってみました。「無限に計算」というのは実際不可能なので, この回路ではテイラー級数の第4項までの近似計算としています。(それでも,それっぽい波形は出ています)
こだわっている所は,全部 ANDゲートやORゲート,フリップフロップ等の汎用ロジックだけで回路を組んでいるところです。。。たしか400個くらいのICを使ったと思います。 なんというか,「原理から理解」してる感じにしたかったので,ちょっと無茶しました。 計算結果はDAコンバータ(これも適当に手作りしたやつです)を通して出力し,オシロで波形を確認しています。 正直,説明不足で何をやっているのか意味不明な動画だと思います。(ぇ
本当は,こんな感じで作った回路の動作解説をしたいと思っていました。でも,その前に必要な数学を解説しておきたくて,でも時間がなくて数学だけ中途半端に解説してしまっていて・・・ という感じになっています。それがこのページです。(すいません)
いずれ,必ず回路動作についても解説を書きます。書きたい,と思っています。