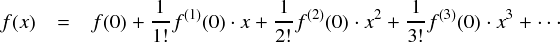
トップページ > フーリエ変換入門(FFT入門) > オイラーの公式(2)
前ページでは,係数が未知の多項式関数を相手にして, 各項の係数を抽出する方法を見ました。今回は多項式関数ではなく,「一般の関数」に関して同じ操作を試してみます。イメージとしては, sin や log なんかを相手にする感じです。
まず,今回は「多項式関数ではない」関数が相手です。これを「 f(x) 」としておきます。 ここで,(強引に)前ページで出てきたのと同じ感じで f(x) を多項式関数の形に展開してみます。
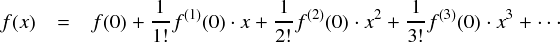
結局,もともと多項式関数ではない関数だったとしても,上のように多項式関数として表現しておかないとコンピュータ上で扱うことはできません。 しかし,上式のように無理やり多項式関数として表わしたものと,元々の f(x) との間には誤差というか,ズレがある気がします。そこで,もとの関数 f(x) と多項式関数っぽく表した上式の差を考えてみます。これは「本物の関数とのズレ」を表しているというイメージです。
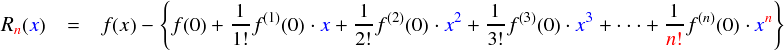
この「ズレ」は,「残留成分」という意味で“Residue”(レザデュ)の頭文字から ”R”と表わすそうです。これを 「剰余項」と呼ぶそうです。 このRに,「本物と,無理やり作ったn次多項式とのズレ」という意味で添え字の “n” を付けて “Rn”と書いています。感覚的には,この n をどんどん大きくしていって無限に続く多項式までもっていけば本物の f(x) に近くなっていく・・・という感じです。そして,もし三角関数や対数関数などの元々多項式関数ではない関数でも,この“Rn”がゼロになれば「多項式関数で表現可能」と言うことができます。最終的にはこれを目指します。
そんなわけで,ここからの主眼は“Rn”ということになります。“Rn”を上手い具合に式で表すために,「ロルの定理」,「ラグランジュの平均値の定理」,「コーシーの平均値の定理」などの道具を揃えておきます。。。
「ロルの定理」は全ての根っこになるような定理で,次のようなものとなっています。
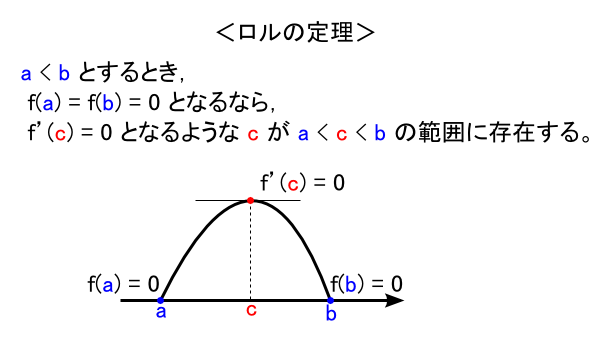
「 f(a) = f(b) = 0 」という条件は,f(x)がa〜bの間でくるっとまわって(?)戻ってくるという感じです。 図では上まわり(上に凸)にしていますが,下へ行ってても(下に凸でも)同じです。 すると,必ず「頂点」のような部分ができます。 「頂点」の部分では,ピンポイントで見れば関数は増えもしないし減りもしません。すごく細かく見れば,平らに見えます。そこでは微分係数がゼロになる気がしますよね・・・ というのがロルの定理です。
一応証明しておきます。
今回の図の場合,x = c となる点では関数が最大値をとります。(a < x < b の間だけ考えます) すると,適当な数 「 h 」を足し算した「 x = c + h 」という座標における関数の値 「 f(c+h) 」は必ず最大値である「 f(c)」 よりも小さくなるはずです。 このことに注意して, x = c における微分係数を求めてみます。 例のごとく,片側極限を右と左からとって,2つの極限が一致すれば微分可能・・・という条件を確かめます。
まずは, h を h → +0 という感じで,正側から近づけます。
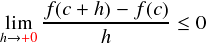
上式で,分母は+0に漸近するということで,一応正です。それに対して分母は小さいf(c+h)から大きいf(c)を引き算しているので負になります。よって,全体として負か,もしくはゼロ・・・という感じになります。
続いて, h を h → -0 と負側から近づける方も考えます。
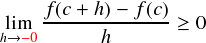
今回は,分母も分子も負なので,全体としては正,もしくはゼロとなります。
以上の2つの片側極限は,f(x) が x = c で微分可能となるためには等しくなる必要があるので,イコールで結ぶことになります。すると,片方はゼロ以上,もう片方はゼロ以下・・・ということで,両者が等しくなるためには 「両方ともゼロ」になるしかありません。
以上をまとめると次のような感じになって,ロルの定理が証明できました。
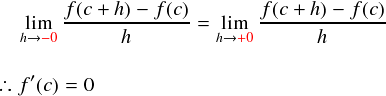
次は,ロルの定理を拡張してラグランジュの平均値の定理に進みます。
「ラグランジュの平均値の定理」は,いわゆる高校数学で習う「平均値の定理」のことです。
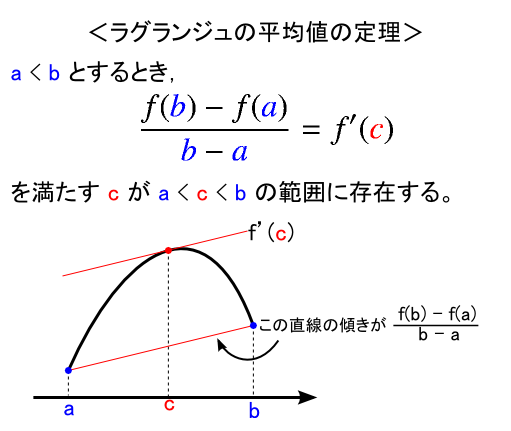
なんというか,ロルの定理の形から,底が持ち上がったような場合の話になっています。 今回は f(a) も f(b) もゼロではなく,好きな値をとることが許されています。その f(a) と f(b) を結んだ直線の傾きは, a < x < b の範囲の f(x) の傾きと,どこかの点で一致する気がします。 ・・・というのがラグランジュの平均値の定理です。
一応証明しておきます。
ロルの定理の形へ無理やり持って行って,最後は証明済みのロルの定理でやっつける・・・という流れにします。
まず,「持ち上がった底」を落とす作業を考えます。 図では最小値である f(a) の部分が全体のオフセットのように効いています。これを引き算してしまいます。 (下図 左→中) さらに,下図の真ん中の図では点 a から左へ行くほど,関数全体に 「(f(b) - f(a))/(b - a)」の傾きで大きくなるオフセットが入っているように見えます。 ちょっと煩雑なので,この傾きを「 k 」と書くことにします。 すると,ある点 x におけるオフセット分は「 k・( x - a ) 」となります。 これを引き算してやれば,もとの関数が x 軸 に足をつけた様な格好になります。(下図 中→右)
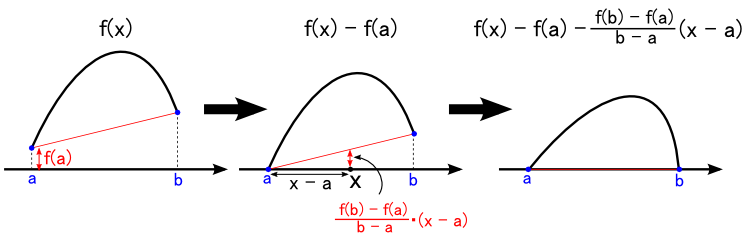
最後の,「関数が x 軸に両足を付ける」ための変形後の式は,ちょっとゴチャゴチャしているので,以後は簡単に g(x) と書いてしまうことにします。 次式で,中カッコの中が引き算されているオフセット分ということになります。
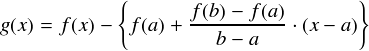
さっきの図から言うまでもないですが,この g(x) はロルの定理を満たします。一応確認しておくと,
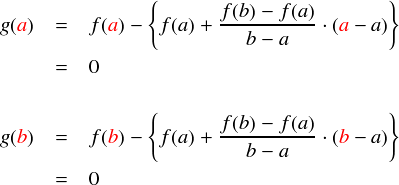
ということで,g(a) = g(b) = 0 が成り立っているので,ロルの定理より, a < c < b の範囲にある c が g'(c) = 0 を満たすことになります。では,具体的にg'(x) を求めてみます。(ただ g(x) を x で微分するだけです。)
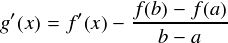
以上から,ロルの定理でいうところの,「 g'(c) = 0 」 という条件は次式のような感じになります。
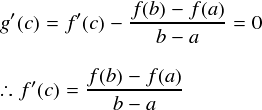
はい。ラグランジュの平均値の定理ができました。f(x) から無理やりロルの定理を適用できるような関数 g(x) を作って, その g(x) に関してロルの定理を適用したところ, f(x) についてのラグランジュの平均値の定理が導出された・・・という流れになっています。
この「コーシーの平均値の定理」は,上でやったラグランジュの平均値の定理をより一般的に拡張した感じになっています。この定理を使って,冒頭で出てきた Rn(x) を導出することになります。
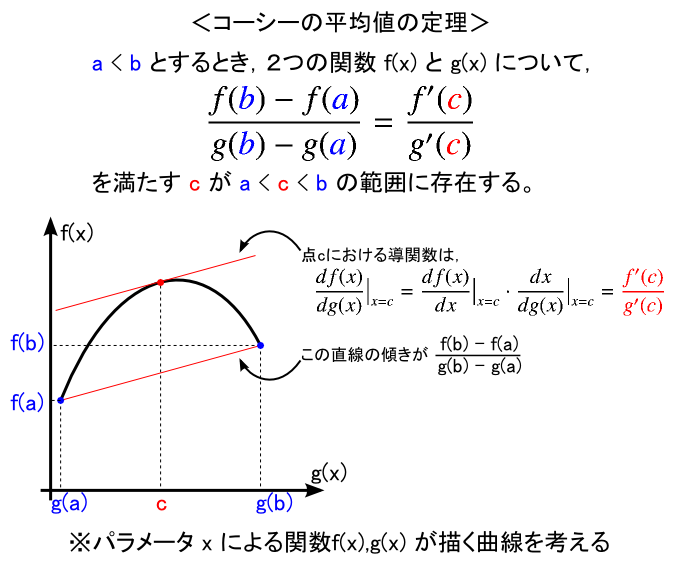
コーシーの平均値の定理はパラメータxによるf(x)とg(x)が作る曲線について, ラグランジュの平均値の定理と同じようなことを言ってるものです。 なので,証明はラグランジュの平均値の定理と同じく,曲線の足をx軸(というか「g(x)軸」ですけど) に落とすような操作を行って,全体に対してロルの定理を使う・・・という感じでもっていきます。
例のごとく,ラグランジュの平均値の定理でやったのと同様にf(x)からオフセット分を差し引いた関数を用意します。 今回は「 g(x) 」という名前を先に使われているので,「 F(x) 」という名前にすることにします。
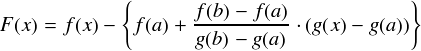
全体的な雰囲気はラグランジュの平均値の定理の時と同じです。中カッコ{ }の中が,差し引いたオフセット分です。 このF(x)はロルの定理が適用できるように用意したものですが,一応F(a) = F(b) = 0 となっているか確認しておきます。
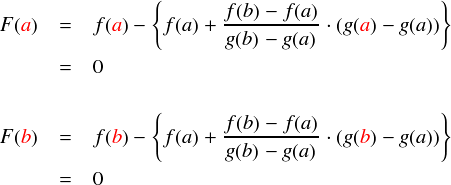
はい。ちゃんとなってます。さらに,F(x)をg(x)で微分するとどうなるかも見ておきます。
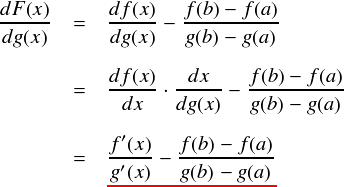
ここで,F(x)にロルの定理を適用すると, a < c < b の範囲にある c がF'(c) = 0 を満たすことになりますので,次式のようになります。
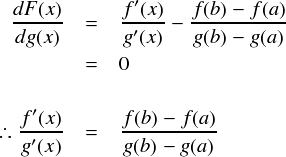
以上で,コーシーの平均値の定理が証明できました。
ここまでで道具が揃ったので,このページの冒頭で出てきた「剰余項 Rn」とは,具体的にどんな形なのかを見ていきます。
まず,「剰余項」とは,本物の関数とそれに似せた多項式関数との差のことでした。
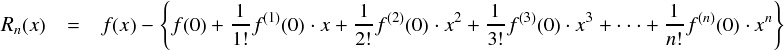
とりあえず,これをどんどん微分していってxが無くなるまで(つまりn+1階まで)導関数を求めていきます。
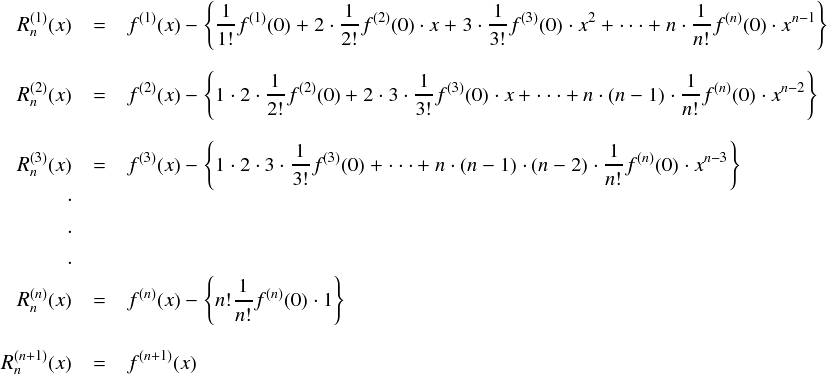
「 Rn はn+1階微分すると簡単な形になる」ということが分かりました。 最初はゴチャゴチャしていた Rn ですが, n+1 階微分すると,単に f(x) を n+1階微分したものと等しくなるようです。この形をなんとかして利用する方向に考えます。。。 たとえば,「コーシーの定理を何度も使うと,どんどん導関数の階数が上がっていくから, n+1 回コーシーの定理を連続して使いまくったら,式は最後に簡単な形になってくれたりするかも・・・」 などと頭の片隅で考えておきます。
次に,xを単に n+1 乗しただけの関数である G(x) というのを考えます。 これは上でやったようにRnをn+1階微分して簡単にしたいので,その相手となるn+1階微分できる関数を用意したいという意図から来ています。n+1階微分できる関数であれば何でも良いので,とりあえず一番簡単な形ということで。
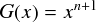
このG(x)についても,n+1階微分まで計算しておきます。とはいっても,自明っぽい感じですけど。。。
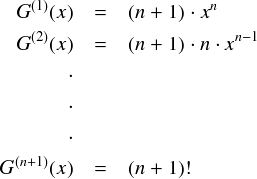
それでは,このRn(x)とG(x)についてコーシーの平均値の定理を使っていきます。 ここで,Rn(0) と G(0) はともにゼロになっています。ちょっと確認しておくと,
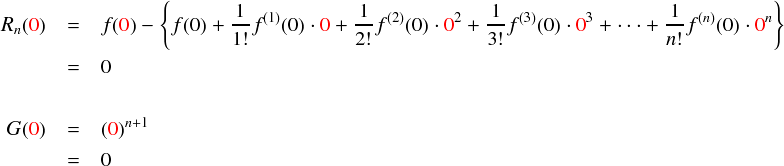
そんなわけで,コーシーの平均値の定理でこの Rn(0) と G(0) を使ってやると, 式が非常に簡単になります。(※「 x1 」というのは,例のごとく 0 < x1 < x を満たす定数です。 )
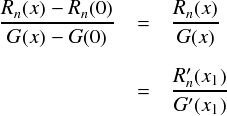
ずっとn+1階微分が出てくるまで,繰り返しコーシーの平均値の定理を使います。 (※ x2 〜 xn+1 は,それぞれコーシーの平均値の定理を満たすような範囲に入っている定数です。とりあえず,微分の階数と同じ添え字をどんどん付けていった感じです。)
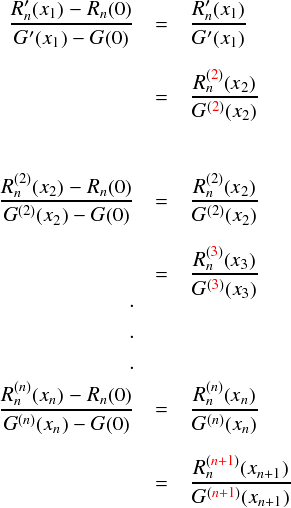
そんなわけで,結局最初から最後までをつなげると次式のようになります。
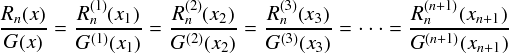
よって,「剰余項」は次のように求まります。
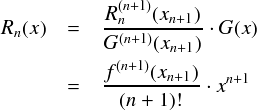
くどいですが, xn+1 は定数で,コーシーの平均値の定理の条件から 0 < xn+1 < x という制限がついています。
やっと剰余項 Rn が導出できました。これが,「本物の関数と多項式関数とのズレ」を表しているということになります。。。 剰余項の表現はこの他にもいろいろあるようで,今回導出した剰余項は 「ラグランジュ型の剰余項」と呼ばれているそうです。
剰余項が求まったところで,改めて「関数の多項式表現」を見てみます。 適当な関数 f(x) を多項式関数の形に展開した場合,一般的には次式のように書かれます。
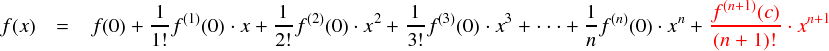
上式は「多項式関数の部分」+「誤差」という形になっています。 また,赤字になっている剰余項の部分に含まれる「 c 」という定数は,コーシーの平均値の定理由来のもので, 0 < c < x をみたします。 この,「関数 f(x) を多項式関数に展開した際に,上式の関係を満たす c が 0 < c < x の範囲に存在する」 ということを「テイラーの定理」と呼ぶそうです。
ここで,項の数 n をどんどん大きくしていくと,より細かく元々の関数 f(x) を表現できそうな気がします。 さらに,n → ∞ の極限で剰余項がゼロになれば,もはや完全に f(x) を再現できたことになります。 その場合,「関数 f(x) はテイラー展開可能」という言い方をするそうです。
次ページでやっと,本来の目的である「三角関数のテイラー展開」をやります。
※ 今回は前ページからの流れで x = 0 における微分係数の f'(x),f(2)(x),f(3)(x),・・・ を使って導出を行ってきました。実際のところ,基準とする x の値は任意で,たとえば x = a を基準にしても今回と同様の証明ができます。具体的には,基準点が x = 0 から x = a にスライドするので, 全ての関数の中で x を 「 x - a 」 に置き換えてやります。本来は(?)この任意の点 a を基準とした形を「テイラー展開」と呼び,今回のように「 x = 0 」を基準とした特殊なケースは「マクローリン展開」と呼ぶそうです。 しかし,両者を「テイラー展開」と呼んでしまう人もいますし,コンピュータでの演算やオイラーの公式の導出なんかではマクローリン展開で十分だったので,今回はマクローリン展開に限ったような形で証明をやりました。。。