トップページ > フーリエ変換入門(FFT入門) > オイラーの公式(1)
ここからは,「ejθ」についての説明です。これの名前というか,呼び方はいろいろあると思うので,とりあえず 「ejθ」と数式のまま書いています。指数関数っぽい見た目ではありますが,これのイメージは回路屋さんにとっては交流信号,半導体屋さんなら波動関数,電波屋さんなら電磁波・・・などなど,様々です。 とりあえずこれがないと何も始りません。 これを使うと,フーリエ解析でもいろいろ計算が楽になったり,様々な性質を考えやすくなります。 (僕は普段これを「波動関数」と呼んでます)
これまでの話とのつながりは無いのですが,一応道具を揃えるということで, 「ejθ」とは何なのか,どうやって作るのか,何の役に立つのか・・・などを確認していきます。 中身としては,テイラー展開とか,そんな感じになってます。 まずは多項式関数の話から始めます。
まずは,xの0乗,xの1乗,xの2乗,・・・と,xを累乗した項をどんどん足していった次のような関数を考えます。
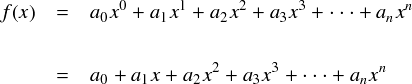
a0,a1,a2,・・・,an というのは各項の係数です。 この形の関数を「多項式関数」と呼ぶそうです。 たとえば「 y = x2 」を表現したければ,a2 = 1 で,それ以外はゼロとします。 また, y = x2 という関数全体を x 方向に 1 だけずらした「 y = ( x - 1 )2 」は,展開すると y = x2 - 2x + 1 となるので,a2 = 1,a1 = -2,a0 = 1 ・・・と係数を設定すれば表現できます。 なんというか,1次関数,2次関数,3次関数,・・・ n次関数を表すための雛型が多項式関数だという感じになっています。
最終的には,sin関数やcos関数をこの多項式関数で無理やり(?)表現することを目標とします。
何故そんなことをするかというと,コンピュータではsin関数やcos関数をそのまま計算できないからです。 実際,コンピュータは足し算と引き算しかできません。 ただ,かけ算は足し算を何度も繰り返せば実現できますし,割り算は引き算を繰り返すことで実現できます。 (“あまり”がマイナスになるまで引き算を続けて,引き算を行った回数をカウンタで数えます・・・) そんなわけで,コンピュータ(ディジタル回路)が実行できる計算は「四則演算だけ」ということになります。 下写真は実際にANDゲート・ORゲートを並べて作った自作の「乗算器」です。 演算器は市販のPCのような複雑な構造ではなく,手づくりでも製作可能です。

上で出てきた「多項式関数」というのは,コンピュータが扱える「四則演算だけ」で構成されているのが重要です。たしか,sin関数やcos関数の定義は「直角三角形の辺の比」が元になっていました。 コンピュータは「直角三角形」をイメージすることはできないので,三角関数を直接計算することは不可能です。しかし,人間が三角関数を「多項式関数」の形に再構成してあげれば,コンピュータでもsin関数やcos関数を計算することができます。 様々な関数を多項式関数の形に表現してコンピュータに計算させれば正確に速く結果が得られるので, 「いろいろな関数を多項式関数の形で表現する」というのは十分実用的な効果が期待できる数学です。
数学とは関係ありませんが,上の「乗算器」は,4段で1セットです・・・ (そのうち作り方を書きます)

とりあえず今の目標は「三角関数を多項式関数で表す」ことになっていますが,実際にどうやれば良いのでしょうか。 三角関数というのは,いわば「未知の多項式関数」ということになります。 未知の多項式関数を相手にするとき,どうやって特定すれば良いのかを考えます。
「未知」というのは何が未知なのかといえば,多項式関数の各「係数」ということになります。 よって,各係数を特定できれば様々な関数を多項式関数で置き換えることができます。 (この流れはフーリエ級数展開の話と似ています・・・) では,多項式関数のa0,a1,a2,・・・,anという係数を取り出す方法を考えてみます。
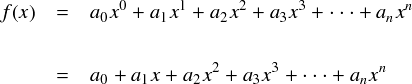
上の多項式関数において,まずは x = 0 を代入してみます。
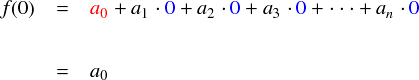
あっけないですが,a0が取り出せました。よって, a0 = f(0) です。 次はa1を取り出したいのですが,さっきは x = 0 を代入するとa1 の項の x がゼロになってしまったため消えてしまったのでした。なので,邪魔な x を消したくなります。。。
ここで,f(x) を 1 回微分してみます。
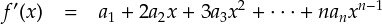
すると,定数項の a0 が消えて,その変わりに a1 が定数項となりました。 よって,ここで x = 0 を代入して・・・
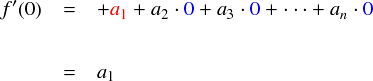
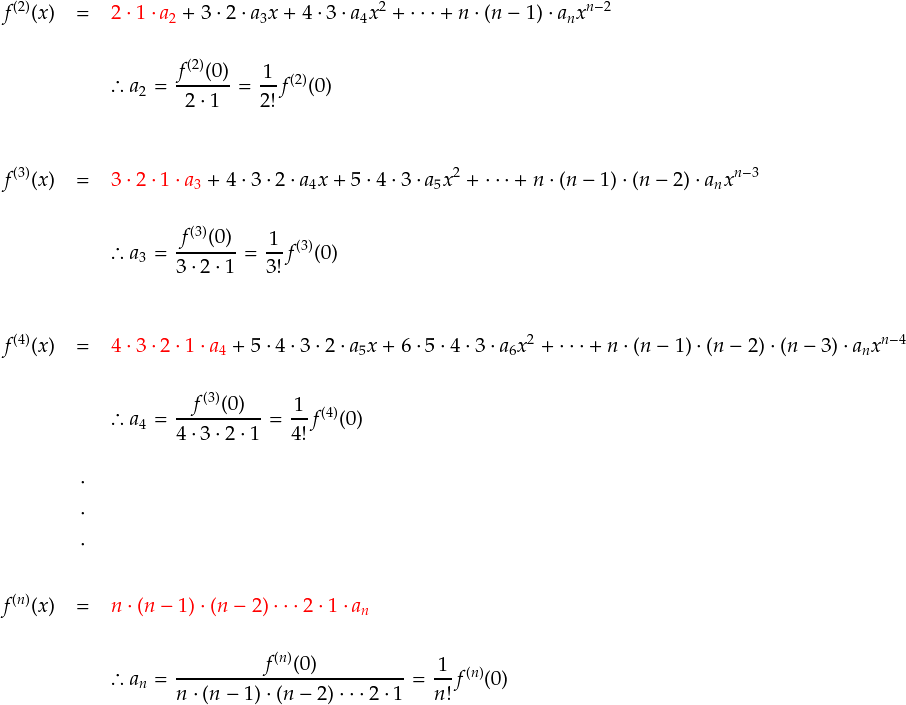
・・・ということで,何階も微分して,その導関数に 0 を代入していけば係数の値が求まることが分かりました。 上式の一番最後の段は,全ての自然数 n で共通な形なので,これを一般形として採用しておきます。
少なくとも,n 次の多項式関数 f(x) であれば,このやり方で全ての係数を求めて完全再現することができます。 f(x) の作り方は,次のようになっています。
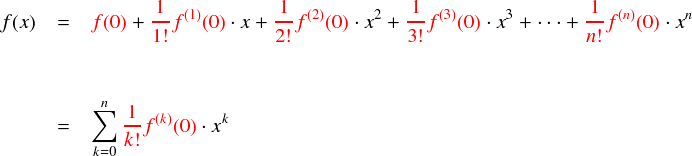
上のような形の級数を「テイラー級数」と呼ぶそうです。 テイラーさん(1685 - 1731)の時代には当然ディジタル回路なんてありませんが, このテイラー級数はコンピュータ上で様々な関数を計算するのに必要不可欠となっています。
このページでは,多項式関数の係数を取り出しただけでした。なんとういか,元が多項式関数なわけですから,スムーズに係数が取り出せて当然という感じです。 次ページでは,元々は多項式関数ではない関数(三角関数など)についても同様の方法が通用するのかを考えます。