
丂栤戣僛儈僫乕儖 俆
丂[俀侾]乮抲偒姺偊偵傛傞娙堈壔乯
丂[俀俀]乮暘夝偵傛傞夝朄乯
丂[俀俁]乮戝彫斾妑乯
丂[俀係]乮俀師嬋慄乯
丂[俀俆]乮偄傠傫側徹柧乯
丂[俀俇]乮嶨戣乯
21乥22乥23乥24乥25乥26

丂[俀侾]乮抲偒姺偊偵傛傞娙堈壔乯
併(x - 1/x) + 併(1 - 1/x) = x 傪夝偗丅
亙Sol亜 A = 併(1 - 1/x)丆B=併(x - 1/x) 偲偍偔偲丄
B + A = x
B - A = (x - 1)/x 乮佹 暘巕偺桳棟壔傪偟偰寁嶼乯
亪 2B = x + (x - 1)/x = (x - 1/x) + 1 = B2 + 1
亪 B = 1丂亪 x2 - x - 1 = 0
亪 x = (1 亇 併5)/2
x 亞 0 備偊 x = (1 + 併5)/2丏丂丂丂丂//
[椶戣]
a丆b丆c 亜 1 偺偲偒丄
榓 S = loga bc + logb ca + logc ab
偺庢傝摼傞嵟彫偺抣傪媮傔傛丅
亙Sol亜 A = log a丆B = log b丆C = log c 偲抲偔偲丄
A丄B丄C 偼偄偢傟傕惓乮佹 a丆b丆c 亜 1乯偱丄
S = B/A + C/A + C/B + A/B + A/C + B/C
傛偭偰憡壛丒憡忔晄摍幃傛傝丄
S 亞 6((B丒C丒C丒A丒A丒B)/(A丒A丒B丒B丒C丒C))1/6 = 6
亪 S 亞 6丏
摍崋偼 A = B = C 偺偲偒丄偮傑傝丄a = b = c 偺偲偒偱丄
傛偭偰嵟彫抣偼俇丏丂丂丂丂丂//
乻嶲峫乼 憡壛丒憡忔晄摍幃乮AM-GM 晄摍幃乯
xi 亞 0 (i = 1丆2丆丒丒丒丆n) 偺偲偒丄
丂(x1x2丒丒丒xn)1/n 亝 (x1 + x2 + 丒丒丒 + xn)/n
摍崋偼 x1 = x2 = 丒丒丒 = xn 偺偲偒丅
亙徹柧 嘥亜 嵍曈傪俧丄塃曈傪俙偲偡傞丅
偐偭偰側幚悢倶偵懳偟偰 ex 亞 x + 1 乮摍崋偼 x = 0 偺偲偒乯
側偺偱丂ex_i/A - 1 亞 xi/A (1亝i亝n)
偙傟傜値屄傪妡偗崌傢偣偰丂
丂e(x_1+x_2+...+x_n)/A - n = en - n = 1 亞 Gn/An
亪 Gn 亝 An丂傛偭偰 G 亝 A丏
摍崋偼偡傋偰偺 倝 偵偮偄偰 xi/A = 1 偮傑傝 x1 = x2 = 丒丒丒 = xn 偺偲偒丅丂//
亙徹柧 嘦亜 x1x2丒丒丒xn = an乮xi亞0乯 偺偲偒 x1 + x2 + 丒丒丒 + xn 亞 an
峏偵 xi = ayi 偲抲偄偰丄
乮仚乯 y1y2丒丒丒yn = 1丆 yi 亞 0 偺偲偒丄y1 + y2 + 丒丒丒 + yn 亞 n
傪帵偣偽傛偄丅
婣擺朄偱帵偡丅
n = 1 偺偲偒丄偁偒傜偐丅 n 偺偲偒壖掕丅
y1y2丒丒丒ynyn+1 = 1丆yi 亞 0 偲偡傞丅
y1 亞 1丆y2 亝 1 偲偟偰傛偄丅
(y1 - 1)(y2 - 1) 亝 0
亪 y1y2 + 1 亝 y1 + y2
亪 (y1 + y2) + y3 + 丒丒丒 + y n+1 亞 (y1y2 + 1) + y3 + 丒丒丒 + yn+1
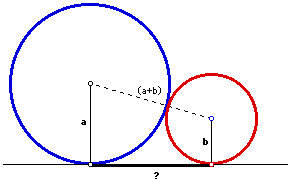 (y1y2)y3丒丒丒yn+1 = 1 側偺偱丄婣擺朄偺壖掕偐傜丄
(y1y2)y3丒丒丒yn+1 = 1 側偺偱丄婣擺朄偺壖掕偐傜丄
(y1y2) + y3 + 丒丒丒 + yn+1 亞 n
傛偭偰丂y1 + y2 + 丒丒丒 + yn+1 亞 n + 1丏
摍崋忦審偺僠僃僢僋偼徣棯丅丂丂丂丂//
値=俀 偺偲偒偵偮偄偰偼
恾偵傛傞愢柧傕偄偔偮偐抦傜傟偰偄傞丅
恾偼偦偺堦椺丅
亂 NOTE 亃 挊柤側暯嬒乮憡壛丒憡忔丒挷榓丒俀忔暯嬒側偳乯傪堦妵偡傞
乽暯嬒偺棟榑乿偑懚嵼偡傞丅乮暯嬒偺岞棟丄暯嬒偺暘椶丄
俶暯嬒乮by Ogihara乯丄倖暯嬒乮俶暯嬒偺堦斒壔乯乯
偦傟偵偮偄偰偼丄悢妛俀偺婰帠(274)乮僐僐乯偐傜係偺婰帠(51)乮僐僐乯傑偱傪嶲徠丅
[椶戣]
摍偟偔側偄惍悢 倶丆倷丆倸 偵懳偟偰丄
5(x - y)(y - z)(z - x)
偼 (x - y)5 + (y - z)5 + (z - x)5 偺栺悢
偱偁傞偙偲傪帵偣丅乮僸儞僩丗 x - y = r丆y - z = s丂偲偍偔偲丄 z - x = - (r + s) 偱偁傞丏乯
[椶戣]
a丆b丆c 偑 a + b + c = 0 傪傒偨偡幚悢偺偲偒丄
丂丂(a5 + b5 + c5)/5 = (a3 + b3 + c3)/3丒(a2 + b2 + c2)/2
偲側傞偙偲傪徹柧偣傛丅
亙Sol亜 旕晧惍悢値偵懳偟偰丄Tn = an + bn + cn 偲偍偔丅
傑偨丄A = ab + bc + ca丆B = abc 偲偡傞丅
a丆b丆c 偼曽掱幃 x3 + Ax - B = 0 偺俁夝備偊丄
xn+3 = -Axn+1 + Bxn 乮n 亞 1乯 傪傒偨偡丅
偙偺偙偲偐傜丄n亞1 偺偲偒丄Tn+3 = -ATn+1 + BTn 偲側傞丅
T3 = (a + b + c)(a2 + b2 + c2 - ab - bc - ca) + 3abc = 3abc
備偊丄T0 = 3 偲偡傟偽丄n亞0 偱惉棫偡傞偙偲偵側傞丅
T0 = 3
T1 = 0
T2 = (a + b + c)2 - 2(ab + bc + ca) = -2A
傛傝丄弴師丄
T3 = 3B丆T4 = 2A2丆T5 = -5AB
偲側傞偺偱丄戣堄偺摍幃傪偊傞丅丂丂//
楙廗栤戣丗丂a丆b丆c 偑 a + b + c = 0 傪傒偨偡幚悢偺偲偒丄
T2丆T5丆T7 偺娫偵惉傝棫偮娭學幃傪媮傔傛丅
楙廗栤戣丗丂x + y + z = 3丆x2 + y2 + z2 = 5丆x3 + y3 + z3 = 7
偺偲偒丄 x4 + y4 + z4 偺抣傪媮傔傛丅
旝暘曽掱幃 dy/dx = f((ax+by+c)/(Ax+By+C)) 偺夝朄偵偮偄偰弎傋傛丅
亙Sol亜 [応崌 侾]丂a丗A 亗 b丗B 偺偲偒丟
楢棫曽掱幃 a兲+b兣+c = 0丆 A兲+B兣+C = 0 偼夝兲丄兣傪傕偮丅
丂丂x=X+兲丄y=Y+兣
偲曄悢曄姺偡傞偲丄
丂丂dY/dX = dY/dy丒dy/dx丒dx/dX = dy/dx = f((ax+by)/(AX+BY))丏 乮摨師宍乯
[応崌 俀]丂a丗A = b丗B 偺偲偒丟
丂丂a/A = b/B = k
偲偍偔偲丄 dy/dx = f((k(Ax+By)+c)/((Ax+By)+C))丏
丂丂v = Ax+By 偲偍偔偲丄 v' = A + By'丏
傛偭偰丂dv/dx = A + Bf((kv+c)/(v+C))丏 乮曄悢暘棧宍乯丂丂//

丂[俀俀]乮暘夝偵傛傞夝朄乯
俆妏惎宍傪嵍俀廳夞傝偵俙俛俠俢俤俙偲偡傞丅
撪妏偺榓 佢俙+佢俛+佢俠+佢俢+佢俤 傪媮傔側偝偄丅
傑偨丄俈妏惎宍偺撪妏偺榓偼壗搙偐丅
亙Sol亜 拞墰偺俆妏宍偺撪晹偺揰俷傪慖傇丅
敿捈慄俷俙偺嵍傑傢傝偺俀夞揮偵傛傝丄
(撪妏偺榓)
= (儮OAB偺撪妏偺榓) + (儮OBC偺撪妏偺榓) + (儮OCD偺撪妏偺榓)
+ (儮ODE偺撪妏偺榓) + (儮OEA偺撪妏偺榓) - 俀兾亊俀
= 兾亊俆 - 俀兾亊俀 = (5-2亊2)兾 = 兾丏 傛偭偰丄侾俉侽搙丅
俈妏惎宍偼俀夞揮僞僀僾偲俁夞揮僞僀僾偑偁傝丄
偦傟偧傟丄 (7-2亊2)兾丆(7-2亊3)兾 偵傛傝 俆係侽搙 偲 侾俉侽搙 偱偁傞丅丂//
惓惍悢 n 偵懳偟偰丄 n = 儼d|n 冇(d) 偲側傞偙偲傪帵偣丅
扐偟丄冇偼僆僀儔乕娭悢偲偡傞丅
亙棯夝亜 G 傪埵悢 n 偺弰夞孮偲偡傞丅
弰夞晹暘孮 C 偵懳偟偰丄偦偺惗惉尦偺慡懱偺廤崌傪 g(C) 偱昞偡丅
捈榓暘夝 G = 伨C g(C) 偑惉傝棫偮偺偱丄
丂丂丂n = 儼C |g(C)| = 儼d|n冇(d)丏丂丂丂丂//
嶰妏宍俙俛俠偺奜愙墌偲撪愙墌偺敿宎傪偦傟偧傟 俼丄倰 偲偡傞偲丄
俼亞俀倰 偱偁傞偙偲傪帵偣丅
乮僸儞僩丗 曈俛俠丄俠俙丄俙俛偺拞揰傪俁捀揰偲偡傞嶰妏宍偺奜怱俹偲偟丄
儮俙俛俠偺柺愊傪儮俹俙俛丄儮俹俛俠丄儮俹俠俙偺柺愊偵暘妱偟偰峫偊傞丅乯
傑偨丄巐柺懱俙俛俠俢偺奜愙媴偲撪愙媴偺敿宎傪偦傟偧傟 俼丄倰 偲偡傞偲丄
俼亞俁倰 偱偁傞偙偲傪帵偣丅
扨埵媴柺忋偺挿偝俀兾枹枮偺暵嬋慄偼敿媴忋偵墶偨傢傞偙偲傪帵偣丅乮僷僩僫儉栤戣乯
亙Sol亜 暵嬋慄傪儭偲偡傞丅儭忋偵俀揰 A 丆B 傪挿偝傪俀摍暘偡傞傛偆偵偲傝丄
A 丆B 偵傛傝 儭 = 儭1伨儭2 偲偡傞丅
B 偺恾偺暯柺儮偵娭偡傞懳徧揰 B' 傪峫偊傞偙偲偵傛傝丄儭1傕儭2傕
暯柺儮傑偱撏偐側偄偙偲偑傢偐傞丅
傛偭偰儭傕儮傑偱撏偐側偄偺偱丄儭偼儮偱俀暘偝傟偨敿媴偺傂偲偮偵娷傑傟傞丅丂丂//
|tA| = |A| 傪婎杮峴楍傪巊偭偰帵偣丅
亙Sol亜 A 偑旕惓懃側偲偒丟 tA 傕旕惓懃偱椉曈偲傕 0 偱惉棫偡傞丅
A 偑惓懃側偲偒丟 A 偼婎杮峴楍偺愊 A = PQ ... RS 偲側傝丄
丂丂丂|tA| = |tStR ... tQtP|
丂丂丂丂丂丂丂丂丂丂= |tS||tR ... tQtP|
丂丂丂丂丂丂丂. . . . . . . .
丂丂丂丂丂丂丂丂丂丂= |tS||tR| ... |tQ||tP|
丂丂丂丂丂丂丂丂丂丂= |S||R| ... |Q||P|
摨條偵偟偰 |A| = |P||Q| ... |R||S|.丂亪 |tA| = |A|.丂丂丂丂//
[椶戣]
|AB| = |A||B| 傪婎杮峴楍傪巊偭偰帵偣丅

丂[俀俁]乮戝彫斾妑乯
師偺戝彫傪寛掕偣傛丅
乮侾乯 7併5 偲 5併7
乮俀乯 e兾 偲 兾e
亙Sol亜 乮侾乯 娭悢 f(x) = (log x)2/x 偵偮偄偰丄
丂丂丂丂丂丂丂f乫(x) = (2log x - (log x)2)/x2
丂丂丂丂丂丂丂f乫(x) = 0 佁 x = 1丆e2
|丂丂丂 1丂 5 7丂 e2
-----+--------------------------------
f'(x)| -丂 0丂丂 +丂丂 0丂丂 -丂丂丂
f(x) | 尭丂丂丂丂 憹丂丂丂丂丂尭
亪 (log 7)2/7 亜 (log 5)2/5丂亪 7併5 亜 5併7丏
乮俀乯 娭悢 f(x) = (log x)/x 偺憹尭傪挷傋傞偙偲偵傛傝丄e兾 亜 兾e丏丂丂//
亙乮俀乯偺暿夝侾亜 兾/e - log兾 = 佺1兾/e (1 - 1/x) dx 亜 0
偲偟偰傕帵偣傞丅丂丂丂丂丂丂//
亙乮俀乯偺暿夝俀亜 兾 偲 e log兾 偺戝彫
偮傑傝 log兾 偲 log(e log兾) = 1 + log(log兾) 偺戝彫
偮傑傝 log兾-1 偲 log(log兾) - log1 偺戝彫偵婣拝偝傟傞偺偱丄
f(x) = logx 偵嬫娫 [1丆log兾] 偱暯嬒抣偺掕棟傪揔梡偟偰傕帵偣傞丅丂//
楙廗栤戣丗丂e併兾 亙 兾併e 傪妋偐傔傛丅
俵傪 (m,n)宆 偺幚峴楍偲偡傞偲偒丄師傪帵偣丅乮T 偼揮抲乯
|MMT| 亗 0 佀 n 亞 m 乮偮傑傝俵偼儓僐挿乯
|MTM| 亗 0 佀 m 亞 n 乮偮傑傝俵偼僞僥挿乯丏
曗戣 幚峴楍俵偵懳偟偰丄 rk(MTM)= rk(MMT)= rk(M).
乮佹乯 MTMx = 0乮x偼幚儀僋僩儖乯 側傜 xTMTMx = 0.
亪 (Mx)T(Mx) = 0.
亪 Mx = 0.
媡偵 Mx = 0 側傜 MTMx = 0.
傛偭偰 Mx = 0 偲 MTMx = 0 偺夝嬻娫偼堦抳偟丄師尦傕堦抳偡傞丅
亪 n - rk(M) = n - rk(MTM). 亪 rk(M) = rk(MTM).
傑偨丄 rk(MMT) = rk((MT)T(MT))
丂丂丂丂丂丂丂丂丂丂丂丂丂丂= rk(MT)
丂丂丂丂丂丂丂丂丂丂丂丂丂丂= rk(M).丂丂//
亙Sol亜 |MMT| 亗 0 佀 n 亞 rk(M) = rk(MMT) = m.
|MTM| 亗 0 佀 m 亞 rk(MT) = rk(MTM) = n.丂丂丂丂丂//
楙廗栤戣丗丂兩傪惓惍悢丄X = { A1,A2, ... ,An }丄L1,L2, ... ,Lm 偼
倣僐偺倃偺晹暘廤崌偲偡傞丅
i = 1,2, ... ,m 偵偮偄偰 | Li |亜兩 偐偮 1亝i亙j亝m 偵懳偟偰
| Li 伩 Lj | = 兩 側傜偽 n 亞 m 偱偁傞偙偲傪帵偣丅乮僸儞僩丗 俵傪
{ L1 , L2 , ... , Lm } 偲 { A1 , A2 , ... , An } 偺愙崌峴楍丄
偮傑傝 倣亊値峴楍 (mij) 偱丄
丂丂丂丂丂丂丂丂丂丂丂丂丂1,丂Aj 伕 Li
丂丂丂丂丂mij = {
丂丂丂丂丂丂丂丂丂丂丂丂丂0,丂otherwise.
偱偁傞傕偺丄偲偟偰忋婰偺栤戣偺寢壥傪揔梡偡傞丅乯
僂僅儕僗偺岞幃 併兾 = lim (22n/併n)亊((n!)2/(2n)!) 傪梡偄偰
僗僞乕儕儞僌偺岞幃 lim n!/(併(2兾)nn+1/2e-n) = 1 傪帵偣丅
乮僸儞僩丗 y = 1/x 偺撌惈傪棙梡偟偨柺愊斾妑偐傜
1/(n+1/2) 亙 佺nn+1dx/x = log(1+1/n) 亙 (1/2)(1/n + 1/(n+1)).乯

丂[俀係]乮俀師嬋慄乯
懭墌忋偺揰俹偵偍偗傞愙慄俴偼 儮俹俥俥乫偺奜妏俹傪俀摍暘偡傞偙偲傪帵偣丅
扐偟丄俥=(-f,0),俥乫=(f,0) (f亜0) 偼徟揰偲偡傞丅
亙Sol亜 奜妏俹偺俀摍暘慄俴乫偑愙慄偵側傞偙偲傪帵偣偽傛偄丅
偙傟偼俴乫忋偺俹埲奜偺揰倃偲偡傞偲丄俻傪俴乫偵偮偄偰偺俥乫偺懳徧揰偲偟偰丄
丂丂俥倃 + 倃俥乫 = 俥倃 + 倃俻 亜 俥俹 + 俹俻 = 俥俹 + 俹俥乫
偱偁傞偙偲偐傜 immediate丏丂丂丂丂丂丂丂//
楙廗栤戣丗丂憃嬋慄丄曻暔慄偵偮偄偰椶帡偺惈幙傪弎傋丄偦傟傪徹柧偣傛丅
曻暔慄 y2 = ax 忋偺俁揰 Pi(xi丆yi) 乮i = 1,2,3乯 偵偍偗傞
朄慄偑
侾揰偱岎傢傞偲偒丄 y1 + y2 + y3 = 0 偱偁傞偙偲傪帵偣丅
亙Sol亜 俁朄慄偺岎揰偺嵗昗傪 (兛丆兝) 偲偡傞偲丄xi丆yi 偼曽掱幃
丂丂丂丂(y - 兝)/(x - 兛) = - 2y/a
傪傒偨偡丅x 偵 y2/a 傪戙擖偟偰惍棟偡傞偲丄
丂丂丂丂2y3 + a(a - 2兛)y - a2兝 = 0
傛偭偰丄夝偲學悢偺娭學偵傛傝丄 y1 + y2 + y3 = 0 偲側傞丅丂丂//
[椶戣]
捈慄 x/a + y/b = 1 偲捈妏憃嬋慄 xy = 1 偑俀揰 P, Q 偱岎傢傝丄偙偺捈慄偼
偙偺憃嬋慄偺慟嬤慄偲 A, B 偱岎傢傞偲偒丄 AP = BQ 傪帵偣丅
亙Sol亜 憃嬋慄偺慟嬤慄偼 x幉 偲 y幉 偱偁傝丄捈慄偲 x幉 偲偺岎揰傪 A 丄
y幉偲偺岎揰傪 B 偲偟偰傛偄丅
P 偲 Q 偺嵗昗傪偦傟偧傟 (x1,y1)丆(x2,y2) 偲偡傞丅
捈慄偺幃偵 y = 1/x 傪戙擖偡傞偲 x2 - ax + a/b = 0
偱丄x1偲x2偼偙偺夝側偺偱 x1 + x2 = a 傪偊傞丅
摨條偵偟偰 y1 + y2 = b 傪偊傞丅
亪 AP2 = (x1 - a)2 + y12
丂丂丂丂丂= (a - x2 - a)2 + (b - y2)2
丂丂丂丂丂= x22 + (b - y2)2
丂丂丂丂丂= BQ2
亪 AP = BQ丏丂丂丂丂丂丂丂//
[椶戣]
懭墌偺捈岎偡傞俀愙慄偺岎揰偺慡懱偼墌傪惉偡偙偲傪帵偣丅
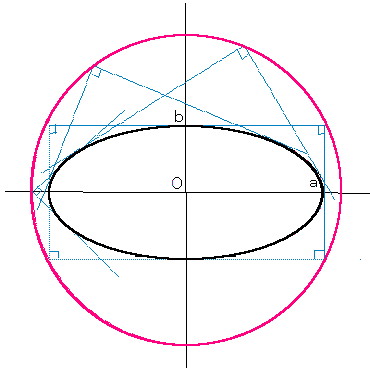 亙Sol亜 懭墌 x2/a2 + y2/b2 = 1 乮 a , b 亜 0 乯 偵偮偄偰帵偣偽傛偄丅
亙Sol亜 懭墌 x2/a2 + y2/b2 = 1 乮 a , b 亜 0 乯 偵偮偄偰帵偣偽傛偄丅
捈岎偡傞俀愙慄偺岎揰傪 P(兛丆兝) 偲偡傞丅
埲壓丄 兛亗亇a 偲偡傞丅
P 傪捠傞捈慄 y = m(x - 兛) + 兝 偑偁偨偊傜傟偨懭墌偵愙偡傞忦審偼丄
懭墌偺幃偵戙擖偟偰摼傜傟傞
(b2 + a2m2)x2 - 2a2m(兛m - 兝)x + a2(m2兛2 - 2m兛兝 + 兝2 - b2) = 0
偑廳夝傪傕偮偙偲偱丄
D/4 = {a2m(兛m - 兝)}2 - a2(b2 + a2m2)(m2兛2 - 2m兛兝 + 兝2 - b2) = 0
亪 (兛2 - a2)m2 - 2兛兝m + (兝2 - b2) = 0
偙偺俀夝 m1丆m2 偲偡傞偲丄夝偲學悢偺娭學偐傜丄
m1m2 = (兝2 - b2)/(兛2 - a2) = - 1
亪 兛2 + 兝2 = a2 + b2
傛偭偰丄揰 P 偼墌 x2 + y2 = a2 + b2 忋偵偁傞丅
傑偨丄 (亇a , 亇b) 傕捈岎偡傞俀愙慄偺岎揰偱偁傞偑丄
偙傟傜傕墌 x2 + y2 = a2 + b2 忋偵偁傞丅丂丂丂丂丂丂丂//

丂[俀俆]乮偄傠傫側徹柧乯
恾偺妏 A 偐傜妏 H 傑偱偺榓偼 4佢R 偱偁傞偙偲傪彮側偔偲傕俁捠傝偱帵偣丅
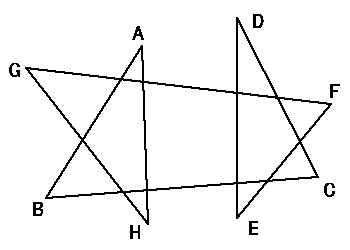
亙Sol 1亜
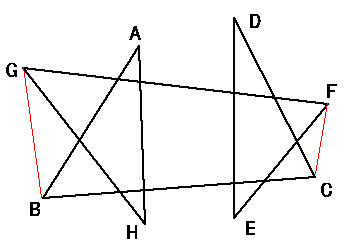
佢A + 佢H = 佢BGH + 佢GBA ,丂佢D + 佢E = 佢CFE + 佢FCD 備偊丅丂丂//
亙Sol 2亜
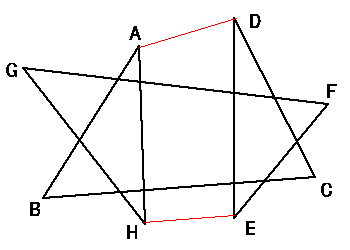
佢A + 佢B + 佢C + 佢D = 4佢R - (佢HAD + 佢EDA),
佢E + 佢F + 佢G + 佢H = 4佢R - (佢AHE + 佢DEH) 備偊丅丂丂丂丂丂//
亙Sol 3亜
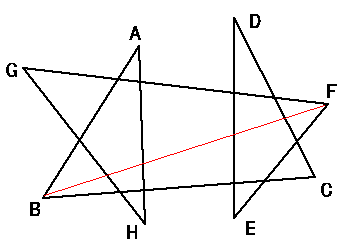
恾偺傛偆偵俀偮偺俆妏惎宍偵暘夝偱偒傞偐傜丅丂丂丂丂丂丂丂丂丂丂丂//
[椶戣]
嶰妏娭悢偺壛朄岞幃 sin(兛+兝) = sin兛cos兝 + cos兛sin兝
cos(兛+兝) = cos兛cos兝 - sin兛sin兝 傪彮側偔偲傕俁捠傝偱帵偣丅
亙Sol 1亜
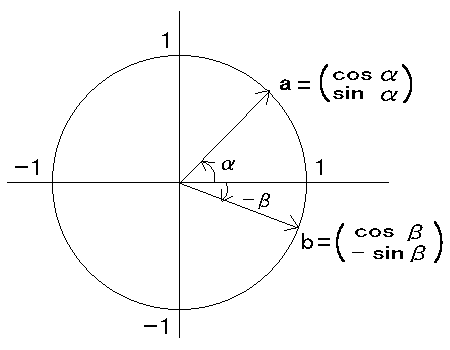
a丒b = cos(兛+兝) = cos兛cos兝 - sin兛sin兝
傑偨丄
sin(兛+兝) = cos{兾/2 -(兛+兝)}
丂丂丂丂丂= cos{(兾/2 - 兛) + (-兝)}
丂丂丂丂丂= cos(兾/2 - 兛)cos(-兝) - sin(兾/2 - 兛)sin(-兝)
丂丂丂丂丂= sin兛cos兝 + cos兛sin兝丂丂丂丂丂丂//
亙Sol 2亜 尨揰偺傑傢傝偺妏兛偺夞揮偲妏兝偺夞揮偺昞尰峴楍傪 俙, 俛 偲偡傞偲丄
尨揰偺傑傢傝偺妏 兛亄兝 偺夞揮偺昞尰峴楍偼 俛俙 偲側傞丅
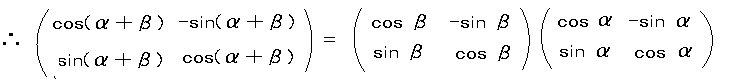
惉暘傪斾傋傞偲壛朄岞幃傪摼傞丅丂丂丂丂丂//
亙Sol 3亜 梌偊傜傟偨幚悢 兛 偵懳偟偰丄
丂丂(x, y) = (cos(兛亄兝), sin(兛亄兝)),
丂丂(x, y) = (cos兛cos兝 - sin兛sin兝, sin兛cos兝 + cos兛sin兝)
偼偄偢傟傕旝暘曽掱幃
丂丂(dx/d兝, dy/d兝) = (- y, x)
偺夝偱弶婜忦審 (x(0), y(0)) = (cos兛, sin兛) 傪枮偨偡丅
傛偭偰丄夝偺堦堄惈偵傛傝堦抳偡傞丅丂丂丂丂丂//
[椶戣]
n 尦廤崌 A 偺晹暘廤崌偼 2n 屄偁傞偙偲傪彮側偔偲傕俁捠傝偱帵偣丅
亙Sol 1亜 A 偺梫慺偵弴斣傪梌偊傞偲 A 偺晹暘廤崌偲 0 丆1 偐傜側傞挿偝 n 偺楍偲偼帺慠偵侾懳侾偵懳墳偡傞偐傜丅乮 A 偺晹暘廤崌慡懱 P(A) 偼懳徧嵎 儮 傪壛朄偲偡傞偙偲偱俀尦懱 {0 丆1} 忋偺儀僋僩儖嬻娫偵側傞偐傜丄偲偄偭偰傕摨偠丅乯丂丂丂丂丂//
亙Sol 2亜 By induction.
n = 0 偺偲偒丗 晹暘廤崌偼嬻廤崌 冇 偺傒偺 1 = 20 屄偱惉棫丅
n 尦廤崌偱惉傝棫偮偲壖掕丅
n + 1 偺偲偒丗 A 偺梫慺傪傂偲偮慖傫偱 x 偲偡傞丅
A - {x} 偺晹暘廤崌偼 2n 屄偱丄A 偺晹暘廤崌偼 A - {x} 偺晹暘廤崌偐偦傟偵 x 傪晅偗壛偊偨傕偺偐偺偄偢傟偐偱偁傞偐傜 P(A) 偺梫慺悢偼 2n+1 偲側傞丅丂丂丂丂丂//
亙Sol 3亜 nC0 + nC1 + . . . + nCn = (1 + 1)n 傛傝丅丂丂丂丂丂//
[椶戣]
挷榓媺悢 儼k=1亣 1/k 偑柍尷戝偵敪嶶偡傞偙偲傪彮側偔偲傕俁捠傝偱帵偣丅
亙Sol 1亜
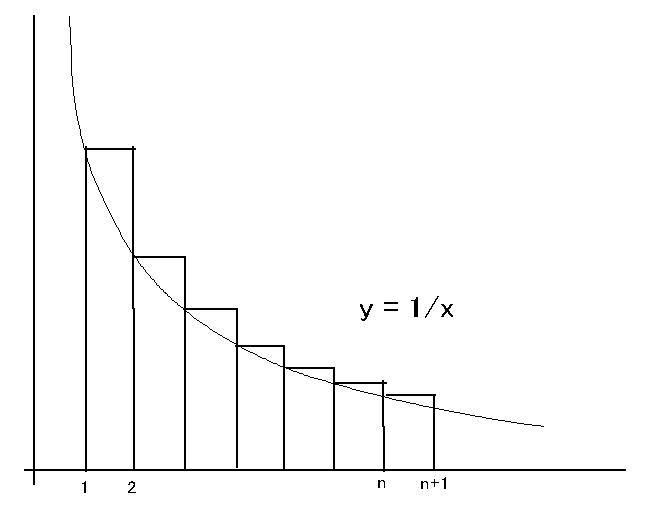
恾偐傜 佺1n 1/x 亙 儼k=1n 1/k
佺1n 1/x = log n 仺 亣 備偊挷榓媺悢偼亣偵敪嶶偡傞丅丂丂//
亙Sol 2亜 戞 n 晹暘榓 Sn 偲偟偨偲偒
S2n - Sn = 1/(n+1) + 1/(n+2) + . . . + 1/2n
丂丂丂丂丂丂丂丂亜 1/2n 亊 n = 1/2
偱 {Sn} 偼僐乕僔乕偺忦審傪枮偨偝側偄偐傜丅丂丂丂丂//
亙Sol 3亜 乮 by Koecher 乯 Sn 偑 兝 偵廂懇偟偨偲偡傞丅
S2n = 1 + (1/3 + . . . + 1/(2n - 1)) + (1/2 + . . . + 1/2n)
丂丂丂丂亜 1/2 + 1/2 + (1/4 + . . . + 1/2n) + (1/2 + . . . + 1/2n)
丂丂丂丂= 1/2 + (1/2)Sn + (1/2)Sn = 1/2 + Sn
n 仺 亣 偲偟偰 兝 亞 1/2 + 兝丂亪 0 亞 1/2丂柕弬.丂丂丂丂丂//
[椶戣]
(sin x)' = cos x 丆(cos x)' = - sin x 傪彮側偔偲傕俁捠傝偱帵偣丅
亙Sol 1亜
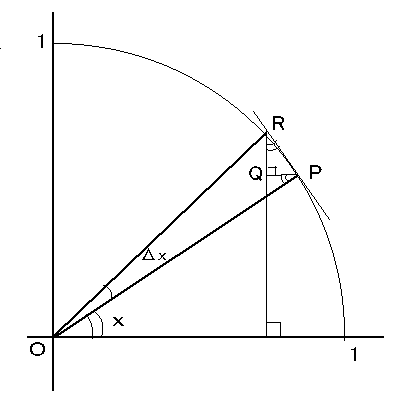
恾傛傝
( sin(x + 儮x) - sin x )/儮x 佮 QR/PR 佮 cos x
儮x 仺 0 偲偟偰 (sin x)' = cos x
傑偨丄 (cos x)' = {sin(兾/2 - x)}' = - cos(兾/2 - x) = - sin x丂丂//
亙Sol 2亜
亙Sol 3亜
[椶戣]
傾儈僟偔偠偱偼偳偺傛偆側暲傃懼偊傕壜擻偱偁傞偙偲傪帵偣丅
亙Sol 1亜
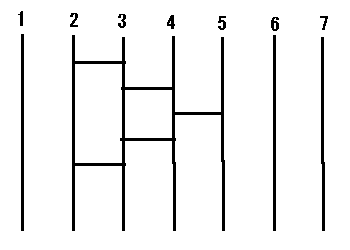
恾偺傛偆偵偡傟偽屳姺 (2 , 5) 傪幚尰偱偒傞丅
摨條偵偟偰偐偭偰側屳姺偑幚尰偱偒傞丅
偳傫側 n 暥帤偺抲姺傕偄偔偮偐偺屳姺偺愊偲偟偰偁傜傢偣傞偺偱丄屳姺傪幚尰偡傞傾儈僟偔偠傪偮側偘傞偙偲偵傛偭偰偳傫側 n 暥帤偺抲姺傕幚尰偱偒傞丅丂丂//
亙Sol 2亜
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂//
亙Sol 3亜 乮by 庣嶌乯
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂//
 [椶戣]
[椶戣]
師偺僺僢僋乮Pick乯偺岞幃傪徹柧偣傛丅
乵僺僢僋偺岞幃乶
懡妏宍偺廃忋偺奿巕揰偺悢傪 B 丆撪晹偺奿巕揰偺悢傪 I
偲偡傞偲丄奿巕懡妏宍 P 偺柺愊 A(P) 偼 B/2 + I - 1 丏
亙Sol 1亜 侾揰 x 偺懡妏宍 P 偵懳偡傞乮壜帇惈偺乯廳傒 wP(x) 傪
x 偺嬤朤偑 P 偵偍偄偰愯傔傞妱崌偱掕媊偡傞丅扨偵 w(x) 偲傕昞帵偡傞丅
乮 x 偑撪揰偺偲偒 1 丆奜揰偺偲偒 0 丆捀揰偺偲偒 (撪妏)/2兾丆
捀揰偱側偄嫬奅揰偺偲偒 1/2丏乯
奿巕懡妏宍 P 偵懳偟偰丄 W(P) = 儼w(x) 乮x 偼奿巕揰乯偲偡傞偲丄
偙傟偼暘妱偵懳偟偰壛朄揑偱偁傞丅
捈妏傪偼偝傓俀曈偑嵗昗幉偵暯峴側奿巕捈妏俁妏宍偵懳偟偰 W(P) = A(P)
偑惉棫偡傞偙偲偼丄偦傟傪埻傓柺愊偑俀攞偱奺曈偑嵗昗幉偵暯峴側奿巕挿曽宍
偵懳偟偰惉棫偡傞偙偲偐傜傢偐傞丅
埲忋偺偙偲偐傜丄W(P) = B/2 + I - 1 傪帵偣偽傛偄偙偲偵側傞丅
W(P) = 儼撪晹 w(x) + 儼廃忋 w(x)
丂丂丂 = I + (n - 2)兾/2兾 + (B - n)兾/2兾丂乮n 偼捀揰偺悢乯
丂丂丂 = B/2 + I - 1 丏丂丂丂丂丂丂丂丂丂丂丂丂丂丂//
亂 NOTE 亃 堦斒偵丄棫懱 S 偲侾揰 x 偵懳偟偰丄S 偵懳偡傞揰 x 偺妏搙 wP(x) 傪
丂丂丂丂lim 兠仺 +0 V(N(x;兠)伩S)/V(N(x;兠)) 乮 V 偼懱愊娭悢 乯
偲偟偰掕媊偱偒傞丅
楙廗栤戣丗丂W(P) = A(P) 偼俁師尦偱傕惉傝棫偮偙偲傪妋偐傔傛丅
尋媶壽戣丗丂惓嶰妏宍偼悕偲偟偰偺捀揰偑偦偺廳怱偱崅偝 0 偺巐柺懱偲偟偰丄
崅偝傪 亣 偵偟偰偄偔偲偒懡柺懱偲偟偰偺捀揰偺妏搙偺憤榓偼偳偺傛偆偵
曄壔偡傞偐挷傋傛丅乮扨挷偵尭彮偟側偄偙偲偵拲堄乯
亙Sol 2亜 偦偺撪晹偵傕曈忋偵傕捀揰埲奜偺奿巕揰傪娷傑側偄奿巕嶰妏宍傪婎杮嶰妏宍偲傛傇偙偲偵偡傞丅
[曗戣]丂婎杮嶰妏宍偺柺愊偼 1/2 偱偁傞丅
乮佹乯傂偲偮偺捀揰偼尨揰偲偟偰堦斒惈傪幐傢側偄丅
懠偺俀捀揰偺嵗昗傪 (a, b)丆(c, d) 偲偡傞丅
働乕僗侾丏(a, b) = (1, 0) 偺偲偒丏d 亙 0 偱偁傟偽婎杮嶰妏宍俹傪倶幉偱愜傝曉偡偙偲偵傛傝 d 亜 0 偲偟偰峫偊傞丅
尨揰偲 (c, d) 偺拞揰俵傪拞怱偲偡傞侾俉侽搙偺夞揮偵傛傞俹偺憸俹乫傕婎杮嶰妏宍偱
暯峴巐曈宍俹伨俹乫偵偼撪晹偵傕曈忋偵傕捀揰埲奜偺奿巕揰偼側偄丅
d 亞 2 偲偡傞偲暯峴巐曈宍俹伨俹乫偵偍偗傞倷嵗昗偑侾偺慄暘偺暆偼侾偱偙偺慄暘忋偵偼奿巕揰偑側偗傟偽側傜側偄偺偱晄崌棟偱偁傞偐傜 d = 1 偱偁傝丄俹偺柺愊偼 1/2 偱偁傞偙偲偑傢偐傞丅
働乕僗俀丏(a, b) 亗(1, 0) 偺偲偒丏俹偺忦審偐傜 a 偲 b 偼屳偄偵慺側偺偱
ap + bq = 1 偲側傞惍悢 p, q 偑懚嵼偡傞丅
堦師曄姺
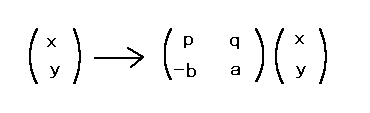
傪峫偊傞丅
偙偺曄姺峴楍偺惉暘偼惍悢偱峴楍幃偼侾偱偁傞偐傜偙偺侾師曄姺偼奿巕揰慡懱傪奿巕揰慡懱偵侾懳侾偵堏偟柺愊傪曐偮丅
峏偵揰 (a, b) 偼揰 (1, 0) 偵堏傞偺偱俹偼働乕僗侾偺婎杮嶰妏宍偵堏傞丅乮曗戣偺徹柧廔傝乯
奿巕懡妏宍俹偼偄偔偮偐偺婎杮嶰妏宍偵暘妱偱偒傞丅偦偺寢壥摼傜傟傞僌儔僼傪俧偲偡傞丅
|V(G)| = I(P) + B(P),丂|E(G)| = { 3(|F(G)| - 1) + B(P) } / 2.
亪 |V(G)|-|E(G)|+|F(G)| = B(P)/2 + I(P) - (|F(G)|-1)/2 + 1.
嵍曈偼僆僀儔乕偺岞幃偵傛傝俀偱丄傑偨曗戣傛傝 (|F(G)|-1)/2 = ( P 偺柺愊 ) 偱偁傞偐傜偙傟傜傪戙擖偟偰惍棟偡傞偲強朷偺幃傪摼傞丅丂丂丂丂丂//
楙廗栤戣丗丂暯柺偵偍偄偰奿巕惓俁妏宍偑懚嵼偟側偄偙偲傪僺僢僋偺掕棟傪巊偭偰帵偣丅乮僸儞僩丗 奿巕懡妏宍偺柺愊偼桳棟悢丏乯
楙廗栤戣丗丂僆僀儔乕偺岞幃傪僺僢僋偺掕棟傪巊偭偰摫偗丅
尋媶壽戣丗丂僺僢僋偺岞幃傪崅師尦偵奼挘偣傛丅

丂[俀俇]乮嶨戣乯
敿宎侾偺俀杮偺墌拰偑偦傟傜偺俀杮偺幉偑岎傢傞傛偆偵捈妏偵岎傢偭偰偄傞丅
嫟捠晹暘偺懱愊傪媮傔傛丅
亙Sol亜 俀杮偺幉偼倶幉丄倷幉偱偁傞偲偟偰傛偄丅
倸幉偵悅捈側奺墌拰偺抐柺偼暯峴俀捈慄傪嫬奅偲偡傞懷忬椞堟備偊丄抐柺偼惓曽宍偵側傞丅
嫟捠晹暘偼扨埵媴懱傪娷傒丄倸幉偵悅捈側抐柺偼惓曽宍偲撪晹偱愙偡傞墌偱丄
柺愊斾偼 2r亊2r丗兾倰2 = 4丗兾
傛偭偰懱愊傕扨埵媴懱偺 4乛兾攞 偱 16乛3 丏丂丂丂丂丂丂//
偳傫側旕帺柧側僲僢僩傕摨堦捈慄忋偵偁傞俁揰傪傕偮偙偲傪帵偣丅
亙Sol亜 侾揰俹傪偊傜傇丅
偳傫側暿偺俀揰俻丆俼偵懳偟偰傕 俹丆俻丆俼 偼嫟態偱側偄偲偡傞丅
揰俻傪摦偐偟偰偱偒傞慄暘俹俻偺慡懱偺崌暪偼
偦偺僲僢僩傪嫬奅偲偡傞帺屓岎嵎偟側偄杽傔崬傑傟偨墌斅偲側傝晄崌棟丅丂//
亂 NOTE 亃 係揰偲偟偰傕惉棫偡傞乮 Morton and Mond 乯丏
墌 O 偵撪愙偡傞巐妏宍 ABCD 偑偁傞丅
AB = a丆BC = b丆CD = c丆DA = d 偲偡傞偲偒 AC 偺挿偝傪a丆b丆c丆d 偱昞帵偣傛丅
亙Sol亜 AC=p丆DB=q偲偡傞丅
屖 ADC忋偵揰 D 乫傪 儮DAC 佭 儮D'CA 偲側傞傛偆偵偲傝 BD' = r 偲偡傞丅
傑偨屖 DCB忋偵揰C 乫傪 儮CBD 佭 儮C'DB 偲側傞傛偆偵偲傞丅
儮ABD' 佭 儮BAC' 偲側傞偺偱 AC' = r 偱偁傞丅
僩儗儈乕偺掕棟傛傝丂pq = ac + bd ---- (1)
丂丂丂丂丂丂丂丂丂丂丂丂丂qr = ab + cd ---- (2)
丂丂丂丂丂丂丂丂丂丂丂丂丂rp = ad + bc ---- (3)
併((1)亊(3)亐(2)) 傛傝丂p = 併( (ac + bd) (ad + bc) / (ab + cd) )丏丂丂丂//
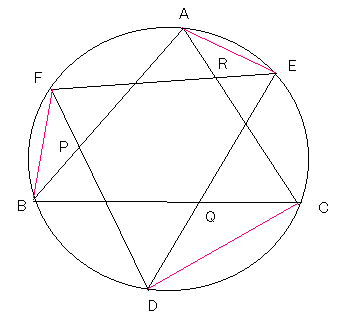 俁妏宍 ABC 偲俁妏宍 DEF 傪傂偲偮偺墌偵偍偗傞岎傢傞傆偨偮偺俁妏宍丄
俁妏宍 ABC 偲俁妏宍 DEF 傪傂偲偮偺墌偵偍偗傞岎傢傞傆偨偮偺俁妏宍丄
FD 偲 BA 丆DE 偲 CB 丆EF 偲 AC 偺岎揰傪弴偵 P 丆Q 丆R 偲偡傞偲偒丄
FP/AR * DQ/BP * ER/CQ = 1 偲側傞偙偲傪徹柧偣傛丅
亙Sol亜 仮ARE 丆仮BPF 丆仮CQD 傪峫偊傞丅
墌廃妏偵傛傝丄
丂丂丂佢EAR = 佢CDQ丂------------ (1)
丂丂丂佢FBP = 佢AER丂------------ (2)
丂丂丂佢DCQ = 佢BFP丂------------ (3)
惓尫掕棟偵傛傝丄
丂丂丂ER/AR = sin 佢EAR/sin 佢AER丂------------- (4)
丂丂丂FP/BP = sin 佢FBP/sin 佢BFP丂------------- (5)
丂丂丂DQ/CQ = sin 佢DCQ/sin 佢CDQ丂------------- (6)
(4)亊(5)亊(6) 偲 (1)丆(2)丆(3) 傛傝媮傔傞摍幃傪摼傞丅丂丂丂丂//
栺悢偵俀傕俆傕帩偨側偄惓惍悢偺偁傞椵忔偼
侽侽丒丒丒侽侾乮侽偼擟堄屄乯傪枛旜偲偡傞偙偲傪帵偣丅
亙Sol亜 惓惍悢傪俙丄侽偼値僐偲偡傞丅
數僲憙尨棟乮偟傢婑偣尨棟乯偵傛傝 俙i 佭 俙j (mod 10n+1)
偲側傞堎側傞惓惍悢倝丄倞 乮i亜j乯 偑懚嵼偡傞丅
俙i - 俙j = 俙j(俙i-j - 1) 偼 10n+1 偺攞悢偱丄壖掕傛傝丄 俙i-j - 1 偼 10n+1 偺攞悢偲側傞丅
傛偭偰 俙i-j 偼 侽侽丒丒丒侽侾乮侽偼値屄乯傪枛旜偲偡傞丅丂丂丂丂丂丂//
偳傫側孮傕攔懠揑乮偍屳偄偵曪娷娭學偑側偄乯側俀偮偺晹暘孮偺崌暪
偲偼側傜側偄偙偲傪徹柧偣傛丅
亙Sol亜 孮俧偑攔懠揑側晹暘孮俙偲俛偺崌暪偲偡傞丅
x 伕 A - B 丆 y 伕 B - A 偲偡傞偲
xy 伕 G - (A 伨 B) = G - G = 冇 偲側傝晄崌棟丅丂丂丂丂//
俧傪俀崁墘嶼 丒 偺偁偨偊傜傟偨戙悢宯偲偡傞丅
俧偺惓懃側 cover丗佁 G = G1 伨 G2 伨 ... 伨 Gs 丆 奺 Gi 偼晹暘乮戙悢乯宯 丆
佂i, Gi 偲 伨j亗i Gj 偼攔懠揑 丏
俧偺師尦丂Dim G丗亖 惓懃側 cover偺戝偒偝 s 偺嵟戝抣 丏
[椶戣]
乮侾乯師尦傪偁偨偊傞俧偺惓懃側僸僼僋偼嬌戝弰夞晹暘宯偺慡懱偱偁傞偙偲傪帵偣丅
乮俀乯Dim G = 3 佀 |G|偼 even. 傪帵偣丅
抂揰乮師悢侾偺揰乯傪挌搙俀僐帩偮栘偼摴偱偁傞偙偲傪徹柧偣傛丅
亙Sol亜 抂揰傪挌搙俀僐帩偮栘偑摴偱側偄偲偡傞丅
偦傟傜偺抂揰傪傓偡傇乮堦堄揑側乯摴傪弅栺乮侾揰偵弅傔傞偙偲乯偟偰傕捀揰悢俀埲忋偺栘偱丄
抂揰偑俀僐埲忋懚嵼偡傞丅偙傟偼晄崌棟偱偁傞丅丂丂丂丂//
[椶戣]
僌儔僼俧偺捀揰暘妱乷 V1 , V2 乸偵傛偭偰掕傑傞僇僢僩僙僢僩冎偵懳偟偰丄
嬌彫偱偁傞偙偲偲桿摫晹暘僌儔僼 G[V1] 丆G[V2] 偑楢寢偱偁傞偙偲偲偼摨抣偱偁傞丄
偲偄偆偙偲傪帵偟側偝偄丅
<徹柧> 楢寢佀嬌彫 偺傒帵偡丅
桿摫晹暘僌儔僼 G[V1] 丆G[V2] 偑楢寢偱冎偑嬌彫偱側偄偲偡傞偲丄
冎偵恀偵娷傑傟傞僇僢僩僙僢僩兞偑偁傞偙偲偵側傞丅
G/(E(G)-兞) 偵偍偄偰兞偺奺曈偼儖乕僾偲側傞偺偱 G/(E(G)-兞) 偼俀慻僌儔僼偱偼側偄丅
偙傟偼晄崌棟丅丂丂丂丂丂//
惓曽宍偼偦傟偲摨偠戝偒偝偺惓曽宍俀偮偱暍偊側偄偙偲傪帵偣丅乮 by 曕埨斵偝傫偺抦傝崌偄偝傫 乯
亙Sol乮奣棯乯亜乮 by 傒傘偆偝傫 乯
Lemma 侾丏 嫍棧倶偺暯峴俀捈慄偵偐偐傞孹偄偨堦曈倶偺惓曽宍偑偦偺俀捈慄偐傜愗傝偲傞慄暘偺挿偝偺榓 仚 偲偡傞偲
丂丂丂丂丂乮 2(併2 - 1)x 亝 乯 仚 亙 x
乮佹乯 暯峴俀捈慄傪忋壓偵 倢丆倣 偲偡傞丅
惓曽宍偼 ABCD 偲偟丄A 偼倢傛傝忋丄B 偼倣傛傝壓偲偐偲偡傞丅
AB 偲倢偺側偡妏傪兤偲偡傞丅
A 偲倢偱偱偒傞嶰妏宍 APQ 偺崅偝傪 h1丆C 偲倣偱偱偒傞嶰妏宍 CRS 偺崅偝傪 h2 偲偟丄
PQ 偲 RS 偺側偑偝傪偦傟偧傟倢1, 倢2偲偡傞丅
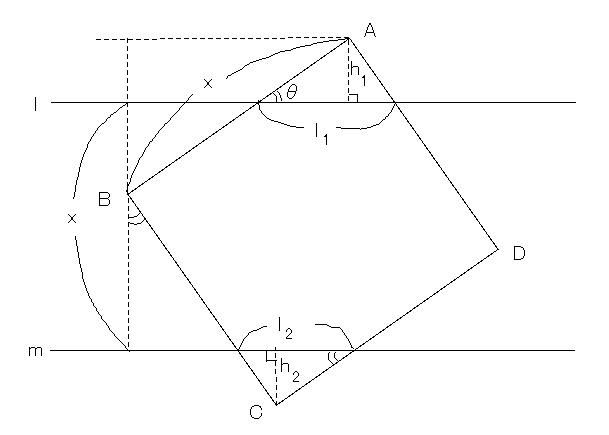
0亙兤亙兾/2 偱 倢i = hi/sin兤cos兤 乮i=1,2乯
仚 = (h1 + h2)/sin兤cos兤
丂 = (x sin兤 + x cos兤 - x)/sin兤cos兤
丂 = x(sin兤 + cos兤 - 1)(sin兤 + cos兤 + 1)/sin兤cos兤(sin兤 + cos兤 + 1)
丂 = 2x/(1 + sin兤 + cos兤)
丂 = 2x/(1 + (併2)sin(兾/4 + 兤))
偙偙偱 兾/4 亙兾/4 + 兤亙 3兾/4 偩偐傜 併2/2 亙sin(兾/4 + 兤)亝 1
傛偭偰梌晄摍幃傪摼傞丅丂丂丂丂//
Lemma 俀丏 侾曈倶偺惓曽宍偺岦偐偄偁偆俀曈偐傜偦偺暯峴偱側偄崌摨側惓曽宍偑愗傝偲傞曈偺挿偝偺榓 亝 倶丏
摍崋偼丄偳偪傜偐偺曈偩偗偑傑傞傑傞惓曽宍偵娷傑傟傞偲偒偵尷傞丅
Lemma 俁丏 侾曈倶偺惓曽宍偺岦偐偄偁偆俀曈偐傜侾曈倶亅倕 乮0亙e亙x乯 偺惓曽宍偑愗傝偲傞曈偺挿偝偺榓 亝倶丏
摍崋偼偳偪傜偐偺曈偩偗偑傑傞傑傞惓曽宍偵娷傑傟傞偲偒偵尷傞丅
偙傟傜偺曗戣偐傜帵偝傟傞丅丂丂丂丂丂丂丂丂丂丂//
[椶戣]
扨埵惓曽宍偼堦曈偑挿偝 1/2 枹枮偺惓曽宍俆偮偱偼暍偊側偄偙偲傪帵偣丅乮 Iberoamerican 2001 乯
惓惍悢 n 偵懳偟偰 (2 n - 1) !! 亝 nn 偑惉傝棫偮偙偲傪帵偣丅
扐偟 (2 n - 1) !! 偼 1 偐傜 2 n - 1 傑偱偺婏悢偺愊偲偡傞丅乮僸儞僩丗 懳徧揑偵
埖偆偵偼丄傑偢 k(2 n - k) 傪昡壙偟偰偍偔丅乯
亙Sol亜 n2 - k(2n - k) = (n - k)2 亞 0 傛傝 k(2n - k) 亝 n2
亪丂((2 n - 1) !!)2 = 儺k=1n ((2 k - 1)(2 n - (2 k - 1)))
丂丂丂丂丂丂丂丂丂丂亝 儺k=1n (n2) = n2n
偙傟傛傝梌晄摍幃傪摼傞丅丂丂丂丂丂丂丂丂丂丂//
亙暿夝亜丂AM-GM 晄摍幃傪巊偊偽 immediate.丂丂丂丂丂//
3併(併(28/27) + 1) - 3併(併(28/27) - 1) = 1 傪帵偣丅
亙Sol亜 嵍曈傪 A 偲偍偔丅
A3 = 2 - A丂亪 (A - 1)(A2 + A + 2) = 0
偙傟偲 A 偑幚悢偱偁傞偙偲偐傜 A = 1.丂丂丂丂丂丂丂丂丂丂丂//
俇偮偺柍棟悢偑梌偊傜傟偨偲偒偦傟傜偺偆偪偺俁偮 a, b, c 偱 a + b, b + c, c + a 傕柍棟悢偱偁傞偺偑偲傟傞偙偲傪帵偣丅
亙Sol亜 偳偺俁揰傕摨堦捈慄忋偵側偄嬻娫偺俇揰傪梌偊傜傟偨俇偮偺柍棟悢偱儔儀儖晅偗偟偰偍偔丅
傑偨丄揰 u 偲 v 傪 u + v 偑桳棟悢偺偲偒愒偺慄暘丄 u + v 偑柍棟悢偺偲偒惵偺慄暘偱寢傃偦偺寢壥摼傜傟傞僌儔僼傪 儭 偲偡傞丅
[ 庡挘 ]丂儭 偵偼愒偐惵偺扨怓俁妏宍偑懚嵼偡傞丅
乮佹乯丂俇揰偺拞偺侾揰 v 傪抂揰偲偡傞曈偼俆杮偁傝偦偺偆偪偺俁杮偼摨偠怓偱偁傞丅
椺偊偽丄偦偺俁杮偼愒偺曈偩偲偡傞丅
偦偺俁杮偺 v 偱側偄抂揰傪 P, Q, R 偲偡傞丅
P, Q, R 傪寢傇曈偺拞偵愒偺曈偑偁傟偽偦傟偲俁杮拞偺俀杮偲偱愒偺扨怓俁妏宍偑偱偒丄 P, Q, R 傪寢傇曈偑偳傟傕惵偺曈偱偁傟偽偦傟傜偑惵偺扨怓俁妏宍偱偁傞丅乮徹廔乯
偝偰丄愒偺扨怓俁妏宍偑偁偭偨偲偡傞偲偦偺捀揰傪 a, b, c 偲偟偰 a + b, b + c, c + a 偑偄偢傟傕桳棟悢偱偁傞偙偲偐傜 (a + b) + (b + c) - (c + a) = 2b 傕桳棟悢偲側傝柕弬偡傞丅
傛偭偰丄惵偺扨怓俁妏宍偑懚嵼偡傞偙偲偵側傝偙傟偼寢榑傪堄枴偟偰偄傞丅丂丂丂//
丂



 (y1y2)y3丒丒丒yn+1 = 1 側偺偱丄婣擺朄偺壖掕偐傜丄
(y1y2)y3丒丒丒yn+1 = 1 側偺偱丄婣擺朄偺壖掕偐傜丄



 亙Sol亜 懭墌 x2/a2 + y2/b2 = 1 乮 a , b 亜 0 乯 偵偮偄偰帵偣偽傛偄丅
亙Sol亜 懭墌 x2/a2 + y2/b2 = 1 乮 a , b 亜 0 乯 偵偮偄偰帵偣偽傛偄丅




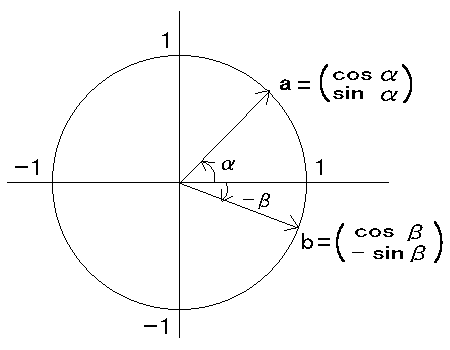
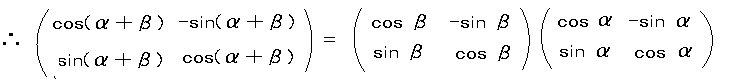
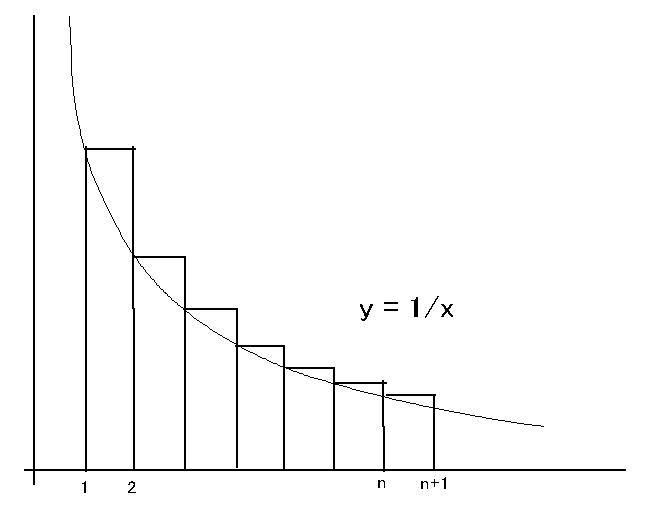
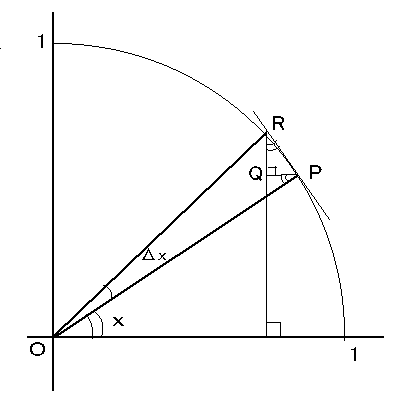

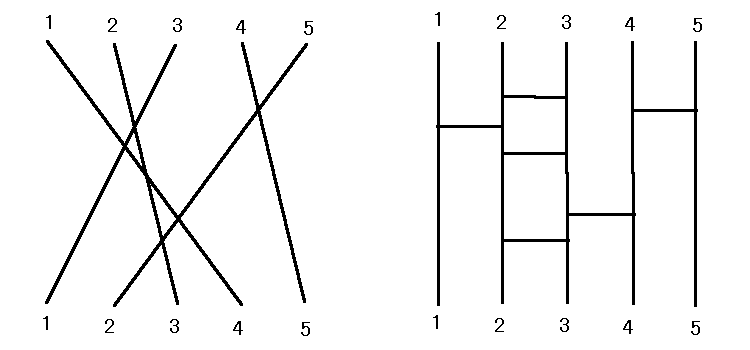

 [椶戣]
[椶戣]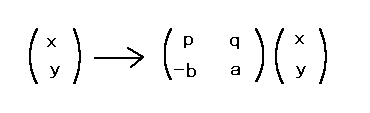

 俁妏宍 ABC 偲俁妏宍 DEF 傪傂偲偮偺墌偵偍偗傞岎傢傞傆偨偮偺俁妏宍丄
俁妏宍 ABC 偲俁妏宍 DEF 傪傂偲偮偺墌偵偍偗傞岎傢傞傆偨偮偺俁妏宍丄