| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 264 | Re:六辺形予想 | coolee | 2000/04/10 05:18 | HOME | 返信 | |
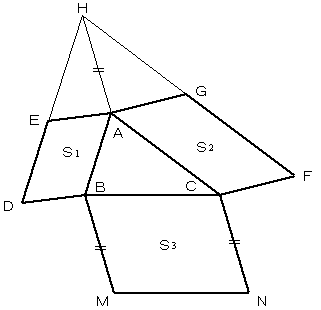
| > > [予想] 平行六辺形の対辺の中点どうしを結んだ3本の直線は1点に会する。
> > 更に1:1をチェバ型で拡張できる。 > > また、逆も成り立つ。 > > > > もし成り立つとしたら特にひとつおきの辺を1点にちぢめるとチェバの定理になります。 > > 平面上で1:1のとき1点に会することは証明できました。 > これのチェバ型はまず問題ないと思います。 ほぼ決着がついたので ホームページの問題ゼミナール1 [1] にまとめておきました。 |
||||||
| 258 | Re:パイン予想の根拠を推察すると | パイン | 2000/04/08 08:06 | 返信 | ||
|
私は素数をフラクタル図形のようなものとしてイメージしています。
素数の分布はランダムではないので期待値という言葉はあまり使いたくないですが、意外とおもしろいかもです。 |
||||||
| 254 | 六辺形予想 | coolee | 2000/04/07 02:20 | HOME | 返信 | |
| [予想] 平行六辺形の対辺の中点どうしを結んだ3本の直線は1点に会する。
更に1:1をチェバ型で拡張できる。 また、逆も成り立つ。 もし成り立つとしたら特にひとつおきの辺を1点にちぢめるとチェバの定理になります。 |
||||||
| 251 | Re:パイン予想の根拠を推察すると | K.Ogihara | 2000/04/06 18:24 | 返信 | ||
| > > これは区間[(P(n))^2,(P(n+1))^2]に含まれる双子素数
> > の組の数です。素数は無限にあるので無限列になります。 > > (P(n)はn番目の素数) > > > > この最小値は1である > > この最大値は∞である > > > > これが俗にいうパイン予想です。 > > 根拠は? (「感覚」としかいいようがなかったらそれでも結構です。) おそらく次のようなことではないか、と私は受け取っています。 // 以下、私の個人的解釈 6N−1 と 6N+1 は、どちらも2の倍数でも3の倍数でもない。 もし N≡±1 (mod 5) 以外――確率は3/5――であれば、どちらも5の倍数ではない。 25 (5の2乗) 以下で、2の倍数でも3の倍数でも5の倍数でもない整数は、素数である。 9<6N+1≦25 を満たすNは3個あり、それらは3/5の確率で双子素数になる、と言える。 同様に N≡±1 (mod 7) 以外――確率は5/7――であれば、どちらも7の倍数ではない。 49 (7の2乗) 以下で、2の倍数でも3の倍数でも5の倍数でも7の倍数でもない整数は、素数である。 25<6N+1≦49 を満たすNは4個あり、(3/5) × (5/7) = 3/7 の確率で双子素数になる、と言える。 これを続けていくと、 ―― 49<6N+1≦121 を満たすNは12個。双子素数となる確率 = (3/5) × (5/7) × (9/11) > 3/11 ―― 121<6N+1≦169 を満たすNは8個。双子素数となる確率 = (3/5) × (5/7) × (9/11) × (11/13) > 3/13 : ―― P(X-1)^2<6N+1≦P(X)^2 を満たすNは (P(X)−1)×2/3 個以上。双子素数になる確率 > 3/P(X) といった具合に一般化でき、"期待値としては" 各区間に少なくとも1つは見込めるのではないか? また、隣り合う素数の間隔には上限がないのだから、区間内のNの個数にも上限がなく、その区間内の双子素数の個数も "期待値としては" 上限がないのではないか? // 以上、私の個人的解釈 どこまでも "期待値" の話でしかないという点が大きな問題で、「各区間に少なくとも1つは見込める」というのはかなり怪しいと考えますが、それほど見当はずれな予想とも言えない、という印象を持っています。 双子素数の個数をすべての区間にわたって "期待値" より小さくしてしまうような "何か" を見落としている可能性は否定できませんけどね。 |
||||||
| 250 | Re:便乗問題 | K.Ogihara | 2000/04/04 12:03 | 返信 | ||
| > {(8,4,2,1),(27,9,3,1),(64,16,4,1),(125,25,5,1)} は基底になりそうですが、そこで問題。
> > [問題] 基底になる理由を示せ。 先輩とのこんな会話が思い出されました。 「未知数4つで等式4つ――こんなの最初から解けるに決まってますよね」 「いやいや、出題側は長年の経験から "4つの等式は必ず独立" と信じて疑わないけど、実際に示そうとすると結構大変じゃないかな」 |
||||||
| 249 | Re:便乗問題 | coolee | 2000/04/04 03:16 | HOME | 返信 | |
| >> {(8,4,2,1),(27,9,3,1),(64,16,4,1),(125,25,5,1)} は基底に
>> なりそうですが、そこで問題。 >> >> [問題] 基底になる理由を示せ。 > > Vandermondeの行列式ですね。 フンイキ的にはランクが n-1 のを非線形的に持ち上げたみたいネ。 チャント定式化したら一般的な定理になりそうですね。 |
||||||
| 248 | Re:便乗問題 | みゅう | 2000/04/04 00:11 | 返信 | ||
| Vandermondeの行列式ですね。
|
||||||
| 245 | 便乗問題 | coolee | 2000/04/01 12:17 | HOME | 返信 | |
| > [生徒の答 その2]
> f(x) = a(x^3) + b(x^2) + cx + d とおくと > 8a + 4b + 2c + d = 1/2 ……[1] > 27a + 9b + 3c + d = 1/3 ……[2] > 64a + 16b + 4c + d = 1/4 ……[3] > 125a + 25b + 5c + d = 1/5 ……[4] > [1]×4 − [2]×6 + [3]×4 − [4] より a + b + c + d = 4/5 > よって f(1) = 4/5 > > *おいおい、いったいどこからそういう発想が出てくる? 君は超能力者か? (1,1,1,1) の (8,4,2,1),(27,9,3,1),(64,16,4,1),(125,25,5,1) による1次結合での表示を使ってるわけですね。 {(8,4,2,1),(27,9,3,1),(64,16,4,1),(125,25,5,1)} は基底になりそうですが、そこで問題。 [問題] 基底になる理由を示せ。 |
||||||
| 243 | ちょっと昔話 | K.Ogihara | 2000/03/31 18:56 | 返信 | ||
| 私の塾講師時代の思い出話を一つ。(今は完全に足を洗っております)
[問題] 3次関数 f(x) が下記を満たすとき、f(1) を求めよ。[10点] f(2) = 1/2 f(3) = 1/3 f(4) = 1/4 f(5) = 1/5 [生徒の答 その1] f(1) = 1 *「3次関数」と明記したにも関わらず、f(x) = 1/x と即断したらしい。 [生徒の答 その2] f(x) = a(x^3) + b(x^2) + cx + d とおくと 8a + 4b + 2c + d = 1/2 ……[1] 27a + 9b + 3c + d = 1/3 ……[2] 64a + 16b + 4c + d = 1/4 ……[3] 125a + 25b + 5c + d = 1/5 ……[4] [1]×4 − [2]×6 + [3]×4 − [4] より a + b + c + d = 4/5 よって f(1) = 4/5 *おいおい、いったいどこからそういう発想が出てくる? 君は超能力者か? [生徒の答 その3] 4次方程式 x(f(x)) - 1 = 0 は x = 2, 3, 4, 5 を解に持ちます。 そこで x(f(x)) - 1 = k(x-2)(x-3)(x-4)(x-5) と表せます。 両辺の定数項を比較すると -1 = 120k なので k = -1/120。 また x = 1 を代入すると f(1) - 1 = 24k なので f(1) = 1 + 24k = 4/5。 これがたったひとつの冴えた解きかた。 *うーん、設定を逆手に取られたなぁ。なかなかお見事。 *ただ、最後の1行は余計だよ。 [生徒の答 その4] (なぜか 4/5, 1/2, 1/3, 1/4, 1/5 と並べて書いてある) (隣同士の項の差を -3/10, -1/6, -1/12, -1/20 と計算した形跡あり) (また隣同士の項の差を 8/60, 5/60, 2/60 と計算した形跡あり) *一瞬「何だこれは」と思ったが、どうやら *「数列 fn の一般項が3次関数なら、第2階差数列は1次関数のはず」 *と考えて、逆算で f(1) を求めようとしたらしいぞ。 # もちろん大多数は一生懸命連立方程式を解いて f(x) を求めていました。 # なお、それぞれの答に何点与えたかは、永遠の謎とさせていただきます。 |
||||||
| 241 | Re:関連する問題2題 | coolee | 2000/03/29 05:04 | HOME | 返信 | |
| >> 以前何かで「メネラウスやチェバはあまり使わないように」とかいうの
>> をみた記憶があるのですが、どうしてでしょうね。 > むかし、寺坂さんの本で > 「射影座標を使って、3点が1直線上にある条件や > 3直線が1点で交わる条件を書き下すと、それがそのまま > メネラウスの定理、チェバの定理になる」 > という話を読んだことがあります。 それは初耳ですが、フンイキとしては射影平面で 3直線が1点で交わる ⇔ 係数行列が非正則 ⇔ |係数行列|=0 なので、例えば対角成分が0だとチェバが出る.ということですね。 > メネラウスの定理、チェバの定理は初等幾何の問題を解く > のに確かに便利ですが、「座標を使って無理やり解く」ような > エレファント性ももっていて、図形の本質を見ぬこうという > 立場からはふさわしくない(?)ということなのでしょうか。 たしかにそういう面があります。 たとえば、平面上のデザルグの定理をメネラウスで示しても あんまりピンと来ない。(でも便利は便利?) |
||||||
| 237 | [Q] 無限級数の和 | iwasi | 2000/03/28 14:52 | 返信 | ||
| Σn-n
に閉じた形の表現はあるのでしょうか? Σの範囲はn=1〜∞です。 |
||||||
| 236 | Re:パイン予想(初級偏) | 安里歩安彼 | 2000/03/28 12:11 | 返信 | ||
|
どうもはじめまして。安里歩安彼といいます。現在中1ですが、後ちょっと
で中2になります。どうぞよろしくおねがいいたいます。 パインの予想、本当にすばらしいと思います。これが成り立ったらすごい ですね。なにせ、最小値1のほうだけでも、即座に双子素数が無限にある ことがみちびかれるのですから。証明or反証はまったく思い浮かびません でしたが、ある程度の様相を把握するには,もしかしたら K=Σpは素数、p^2〜p+1^2の間に存在する双子素数のどれかひとつ の組の逆数 で定められるKがどのへんを動くかということを調べてみると面白いのではないのでしょうか。ただ、僕はこの評価については,おおざっぱなことしかわかりませんでした。また、cooleeさんがおっしゃるように,この予想と、 Riemann予想を整数論的にいったものに何らかの関係があるとすれば,もしかしたらゼータ関数のような、ひじょうに高度な道具をつかって解決されるのかもしれません。でも、もしかしてひょっとしたら,エルデシュのような数学者が、ものすごい初等的なやりかたで解決してしまうかもしれませんね。ということで、なんともまとまりの無いいいかげんなコメントになってしまいましたが,遅らせていただきます。 |
||||||
| 235 | Re:パイン予想(初級偏) | パイン | 2000/03/27 18:01 | 返信 | ||
| >
> 根拠は? (「感覚」としかいいようがなかったらそれでも結構です。) はい!感覚が大きいです。私の場合は論理は後からこじつけてしまいます。 論理と言っても 「隣り合うメタ双子素数と重なり合うメタ双子素数の結合法則」といった自分にしか解らない(自分でもよくわからない!?)怪しいものです・・・ 感覚的にはガウスが100だか1000の区間ごとに素数を数えてた事を知って 「ずいぶん変なところで区切ってるなあ」と違和感を感じました。もろ十進数に依存してる感じです それよりはp^2で区切った方が自然な感じがします そこで最初の区間[2^2,3^2]の性質を考えると双子素数が1組あるという性質くらいしか思い浮かびません、 「これこそ自然数の性質の最小単位だ!そして全ては最小単位の組み合わせに違いない」 なんて思ってしまいました。 |
||||||
| 233 | A Conjecture | coolee | 2000/03/25 18:49 | HOME | 返信 | |
| > 問題: どんな(平面)5角形についてもある内点が存在して
> 頂点までの距離の合計が周長より小さくできるでしょうか? > > ♯ 三角形と四角形については、そのような内点が必ず存在します。 次のような反例をメールでいただきました。 反例(by 前原) ひとつの内角が120度で残りの4頂点が 2つずつ十分近い5角形。 // 「ひとつの内角が120度以上」としても同様に反例ができるので次。 予想 どの内角も120度未満のどんな平面5角形についても、 ある内点で頂点までの距離の和が周長より小さいのが存在する。 |
||||||
| 230 | パイン予想(初級偏) | パイン | 2000/03/24 20:20 | 返信 | ||
|
1,2,2,4,2,7,2,4,8,2,11,7,3,11,13,13,5,19, 11,3,15,14,14,21,15,7,10,6,11,42,12,27,6,45,10,20,17,21,23,25,13,49,7,20,まだまだ続きますが疲れたので この辺で これは区間[(P(n))^2,(P(n+1))^2]に含まれる双子素数の組の数です。素数は無限にあるので無限列になります。 (P(n)はn番目の素数) この最小値は1である この最大値は∞である これが俗にいうパイン予想です。 ーーーーーーーーーーーーーーー定義ーーーーーーーーーーーーーーーーー メタ双子素数 ある自然数nの±zが素数であるとき n=M(z)と表し 「nはメタ双子素数(z)の核である」と読む。 M(0)は単体の素数の集合を意味する M(1)は双子素数の集合を意味する 重核とは 5=M(0)、かつ、5=M(2) このようなとき 5=M(0,2)と表し 「5はメタ双子素数(0,2)の重核である」と読む ーーーーーーーーーーーーーーーーーーーーーーーーーーーー ゴールドバッハ予想のパイン表現 「2以上の自然数はメタ双子素数の核である」 次回はメタ双子素数の結合法則から更なる予想を述べさせて頂きます ps 私くし数腕が未熟なので、こっ恥ずかしいです。 |
||||||
| 210 | Re:やさしい?NO.10 | coolee | 2000/01/03 02:34 | HOME | 返信 | |
| > > <モンダイ> 2円 C1、C2 の共通割線上の点Pからのそれら2円への接線の接点P1、P2に対して PP1 = PP2.
> > という性質を使って示せる命題を述べよ。 > > 例 ΔABCに対して、Aから辺BCに下ろした垂線の足D、Dから辺AB,ACに下ろした垂線の足をそれぞれE,Fとする。 > 直線EFとΔABCの外接円との交点をG,Hとすると、AD=AG=AH. 交わる2円にかんする性質、というのもけっこうおもしろいですね。 たとえばこんなのもあります。 Suppose two circles intersect in A and B. A point P is selected on one of the circles on the outside arc. P is projected through A and B to determine chord CD on another circle. Prove that no matter where P is chosen on its arc, the length of the chord CD is always the same. (→ココ) |
||||||
| 209 | Re:やさしい?NO.12 | coolee | 2000/01/03 00:29 | HOME | 返信 | |
| > > > <モンダイ> 「結合法則」の成り立つ例を少なくとも30個あげてそれを証明せよ。
> > > ♯ 「少なくとも30個」にこだわらなくてもいいですが..。 > <原始的な例> a*b=b とする。 > (a*b)*c=b*c=c=a*c=a*(b*c). // 幾何学的には点の移動による演算がモデルになってますね。 カテゴリー(圏)論なんかで使えないかなァ..。 |
||||||
| 207 | やさしい?NO.14 | coolee | 1999/12/31 07:53 | HOME | 返信 | |
| <モンダイ> モーレーの定理をベクトルもしくは複素数を使って証明せよ。
モーレーの定理についてはたとえばココ. |
||||||
| 206 | Re:やさしい?NO.12 | coolee | 1999/12/31 04:21 | HOME | 返信 | |
| > > <モンダイ> 「結合法則」の成り立つ例を少なくとも30個あげてそれを証明せよ。
> > ♯ 「少なくとも30個」にこだわらなくてもいいですが..。 > > どんな解がくるんだろう..。楽しみっ。 フゥ〜ム 見た目より難問だったみたいですね。 結合法則1個に理論1個が対応してると言っても華厳の滝、もとい過言ではないですからねぇ..。 |
||||||
| 205 | Re:やさしい?NO.12 | coolee | 1999/12/29 19:29 | HOME | 返信 | |
| > > <モンダイ> 「結合法則」の成り立つ例を少なくとも30個あげてそれを証明せよ。
> > ♯ 「少なくとも30個」にこだわらなくてもいいですが..。 > > <例> Tをツリー(非輪状なグラフ)、その頂点集合V(T)、O∈V(T)とする。 > V(T)における次の演算は結合的。 > > A+B = パスOAとパスOBのOからの最後の共通点. > > 種明かししちゃうと..うっぷ、、。 たとえば、Oを最小元とするように自然に半順序集合にしたとき 下限(infimum)をとる演算になってます。 |
||||||
| 200 | Re:やさしい?NO.12 | coolee | 1999/12/27 00:33 | HOME | 返信 | |
| > <モンダイ> 「結合法則」の成り立つ例を少なくとも30個あげてそれを証明せよ。
> ♯ 「少なくとも30個」にこだわらなくてもいいですが..。 <例> 集合Sの部分集合A,Bに対して A ∇ B = (A Δ B)c は結合的。(Δは対称差) (∵) A ∇ B = Ac Δ B = A Δ Bc なので (A ∇ B) ∇ C = ((A Δ B)c Δ C)c = (A Δ B)cc Δ C = A Δ B Δ C = A Δ (B Δ C)cc = (A Δ (B Δ C)c)c = A ∇ (B ∇ C). // ♯ ホームページの数学の記事(114)(ココ)参照。 |
||||||
| 199 | Re:やさしい?NO.12 | coolee | 1999/12/25 19:51 | HOME | 返信 | |
| > > <モンダイ> 「結合法則」の成り立つ例を少なくとも30個あげてそれを証明せよ。
> > ♯ 「少なくとも30個」にこだわらなくてもいいですが..。 > どんな解がくるんだろう..。楽しみっ。 <原始的な例> a*b=b とする。 (a*b)*c=b*c=c=a*c=a*(b*c). // |
||||||
| 196 | Re:やさしい?NO.13 | coolee | 1999/12/24 23:53 | HOME | 返信 | |
| > ∂A := {A の閉包}-{A の内点} と定義するのだと解釈しましたが、それなら答えは No.
> 反例 > X = R (実数全体に普通の位相を入れたもの) > A = {0} > この場合、∂A = {0}, ∂∂A = {0} != φ 正解です。ホモロジー論を最初に考えた人(ポアンカレ?)はやはりスゴイですね。 |
||||||
| 195 | Re:やさしい?NO.13 | クリーム | 1999/12/24 21:22 | HOME | 返信 | |
| ∂A := {A の閉包}-{A の内点}
と定義するのだと解釈しましたが、それなら 答えは No. 反例 X = R (実数全体に普通の位相を入れたもの) A = {0} この場合、∂A = {0}, ∂∂A = {0} != φ |
||||||
| 194 | やさしい?NO.13 | coolee | 1999/12/24 19:52 | HOME | 返信 | |
| <モンダイ> 位相空間Xの部分集合Aに対してその境界を∂Aで表示する。
∂∂A=φは成り立つか? |
||||||
| 193 | Re:やさしい?NO.10 | coolee | 1999/12/24 16:34 | HOME | 返信 | |
| > <モンダイ> 2円 C1、C2 の共通割線上の点Pからのそれら2円への接線の接点P1、P2に対して PP1 = PP2.
> という性質を使って示せる命題を述べよ。 例 ΔABCに対して、Aから辺BCに下ろした垂線の足D、Dから辺AB,ACに下ろした垂線の足をそれぞれE,Fとする。 直線EFとΔABCの外接円との交点をG,Hとすると、AD=AG=AH. 証明は、まずAG=AHを示します。次にAD=AGを示すところでモンダイの性質が使えます。 |
||||||
| 190 | やさしい?NO.12 | coolee | 1999/12/23 15:09 | HOME | 返信 | |
| <モンダイ> 「結合法則」の成り立つ例を少なくとも30個あげてそれを証明せよ。
♯ 「少なくとも30個」にこだわらなくてもいいですが..。 |
||||||
| 168 | Re:やさしい?NO.4 | coolee | 1999/12/14 02:30 | HOME | 返信 | |
| > QAの延長とPBの延長の交点をRとするとRQPは正三角形。
> QP上2つの正三角形の共有点をXとすると対称性からRX=QB > 同じようにRX=PA ゆえに成立。 Good!です。 <別解>
B
A /\
/\ / \
/ \ / \ AP = QB' = QB.
Q /____\/______\ P
\ /
\ /
\ /
\ B' // |
||||||
| 167 | Re:やさしい?NO.4 | みゅう | 1999/12/14 00:43 | 返信 | ||
| QAの延長とPBの延長の交点をRとするとRQPは正三角形。
QP上2つの正三角形の共有点をXとすると対称性からRX=QB 同じようにRX=PA ゆえに成立。 だめ? |
||||||
| 166 | やさしい?NO.4 | coolee | 1999/12/13 22:30 | HOME | 返信 | |
B
A /\
/\ / \
/ \ / \
Q /____\/______\ P
図は線分上の2つの正三角形である。 AP = BQ を、通常の学校か塾での三角形の合同による証明以外で示せ。 |
||||||
| 164 | Re:やさしい? | coolee | 1999/12/13 20:55 | HOME | 返信 | |
| > 複素数の導入の仕方にもいろいろ考えられます。
> たとえば、複素数の相等「 a + bi = c + di ⇔ a = c かつ b = d 」 > を「定義」に入れてる本が多いですが、「定理」にしたほうがいいのでわ? オオザッパにしか考えてませんが a + 0i = a とし 0 + bi は bi と略記する,ぐらいでいいみたい。 もちろん四則演算は通常のように定義しとくとか。 これぐらいの設定でけっこう遊べる公理系に変貌します。 |
||||||
| 162 | やさしい?NO.3 | coolee | 1999/12/13 04:34 | HOME | 返信 | |
<モンダイ>
置換 (1 2 ... n) が偶置換 ⇔ 順列 <i1,i2,...,in> が偶順列. (i1i2...in)を示せ。 |
||||||
| 159 | Re:やさしい? | coolee | 1999/12/13 02:22 | HOME | 返信 | |
| > > <モンダイ> 複素数 α = a+bi が0でないとき「極形式表示」 α = r(cosθ+i sinθ) (r>0)
> > は一意的であることを証明せよ。 複素数の導入の仕方にもいろいろ考えられます。 たとえば、複素数の相等「 a + bi = c + di ⇔ a = c かつ b = d 」 を「定義」に入れてる本が多いですが、「定理」にしたほうがいいのでわ? |
||||||
| 155 | Re:やさしい? | coolee | 1999/12/08 23:08 | HOME | 返信 | |
| > <モンダイ> 複素数 α = a+bi が0でないとき「極形式表示」 α = r(cosθ+i sinθ) (r>0)
> は一意的であることを証明せよ。 <SOL> r1(cosθ1+i sinθ1) も r2(cosθ2+i sinθ2) もαの極形式とする。 r2(cosθ2+i sinθ2)/r1(cosθ1+i sinθ1) = 1 ∴(r2/r1)*(cos(θ2-θ1)+i sin(θ2-θ1)) = 1 + 0i ∴(r2/r1)*cos(θ2-θ1) = 1 -------(1) かつ (r2/r1)*sin(θ2-θ1) = 0 -------(2) (2)より sin(θ2-θ1) = 0 なので θ2-θ1 = 2nπ または (2n+1)π (n は整数) θ2-θ1 = (2n+1)π だと (1)より 1 = (r2/r1)*cos(2n+1)π = -(r2/r1) < 0 となって不合理。 よって θ2-θ1 = 2nπ. これを(1)に代入して r2/r1 = 1 ∴ r1 = r2. // |
||||||
| 150 | やさしい? | coolee | 1999/12/06 19:50 | HOME | 返信 | |
| <モンダイ> 複素数 α = a+bi が0でないとき「極形式表示」 α = r(cosθ+i sinθ) (r>0)
は一意的であることを証明せよ。 |
||||||
| 147 | Re:集合論的幾何のもんだい | coolee | 1999/12/05 03:07 | HOME | 返信 | |
| > 一般に2元体G2={0,1}上のベクトル空間Vの部分空間Wとそのひとつのコセット(剰余類)a+W に対して W∪a+W はVの部分空間になります。
> 集合空間(対象差Δで閉じてる空間)でseparateしないδの全体がそのモデルになっています。 わりとポピュラーな例だと位相空間論で まじわりが空でない連結集合の族の合併も連結、というのの証明で separateという概念が効力を発揮してる、と言えばピンとくるかも。 |
||||||
| 144 | Re:集合論的幾何のもんだい | coolee | 1999/11/29 00:34 | HOME | 返信 | |
| > シグマをsデルタをdで代用します。
あんまり代用しないほうがいいとおもいます。 変換するかコピー&ペーストで。 > (s2△d))-(s1△d)=(s2-s1)-d > (s1△d))-(s2△d)=(s2-s1)まじわりd > より明らかに成立。で、どうでしょう。 この問題の場合、基本的な性格をもった問題なので、あまり知られていない集合論的等式を使うときは その証明も書いておかないとあまり意味がないようにおもいます。 でないと、極端な話、なんでも「明らか」になってしまいます。 |
||||||
| 142 | Re:集合論的幾何のもんだい | みゅう | 1999/11/28 23:51 | 返信 | ||
| シグマをsデルタをdで代用します。
(s2△d))-(s1△d)=(s2-s1)-d (s1△d))-(s2△d)=(s2-s1)まじわりd より明らかに成立。で、どうでしょう。 |
||||||
| 141 | Re:集合論的幾何のもんだい | coolee | 1999/11/28 20:15 | HOME | 返信 | |
| > それと例を一つお願いします。
あまり個人的に立ち入った研究にはふれない方針ですが.. 一般に2元体G2={0,1}上のベクトル空間Vの部分空間Wとそのひとつのコセット(剰余類)a+W に対して W∪a+W はVの部分空間になります。 集合空間(対称差Δで閉じてる空間)でseparateしないδの全体がそのモデルになっています。 |
||||||
| 140 | Re:集合論的幾何のもんだい | coolee | 1999/11/28 15:52 | HOME | 返信 | |
| > 排他的って?
お互いに包含関係がないことです。(記事番号125でのべてあります) 記号としては⊂と⊃をタテに並べて縦棒|で串刺しにしたものを私は使ってます。 >それと例を一つお願いします。 例.σ1={1,2,3},σ2={1,2,3,4,5},δ={1,3,4,6} とか. ♯ 動機はグラフのサイクルたちの分布に対する対称差Δの影響とか。 ♯ みゅうさんも集合族の幾何やってみませんか?(って、ばくぜんとしてますが。) |
||||||
| 139 | Re:集合論的幾何のもんだい | みゅう | 1999/11/28 09:28 | 返信 | ||
| 基礎的な疑問
排他的って?いろいろ考えていたら歯が痛くなってきたので質問することにしました。それと例を一つお願いします。 |
||||||
| 138 | 集合論的幾何のもんだい | coolee | 1999/11/23 16:30 | HOME | 返信 | |
| σ1,σ2をset E の σ1⊆σ2 なるsubsetsとする。
set E の subset δ が (σ1,σ2)の cut:⇔ δΔσ1とδΔσ2は排他的. set E の subset δ が Eのsubsetεをseparateする:⇔ δ∩ε≠φかつε-δ≠φ. <もんだい> 次は同値である事を示せ。 (1) δは (σ1,σ2)の cut. (2) δは σ2-σ1をseparateする. ♯ 「集合論的幾何」というのはわたしの造語です。 |
||||||
| 104 | Re:微積分の基本定理の乗法版 | Dr.G | 1999/11/05 05:27 | 返信 | ||
| > 公式として
> > ・ log f’(x) = (log f(x))' > > ・ e^f'(x) = (e^f(x))’ > > とするとバランスがいいかも。 簡単な系 (e^(e^x))’=e^(e'(x))=e^(e^x) |
||||||
| 102 | Re:4元数の代数的構造を教えて〜 | coolee | 1999/11/05 01:50 | HOME | 返信 | |
| おひさしぶりです。
> 3次元空間中のベクトルxを、単位ベクトルwを軸として、反時計方向にΘ回転したものが、ベクトルの基底を、4元数と見なして計算すると、 > gxg*と表せるという事があるのですが、【g=cos(Θ/2)+wsin(Θ/2)、g*は、gの共役4元数】 > aba*(aa*=e)の形って、結構いろんな所で見かけるのですが、 > 4元数の場合に限定した場合のこの形が意味することの、すべてが知りたいのですが・・・ H ・・・4元数 a1+bi+cj+dk の全体(非可換体) H_0 ・・・純4元数 bi+cj+dk の全体 U ・・・ノルムが1の4元数の全体 SO(3) ・・・行列式が1の3次直交行列の全体 とします。 I_x(y):= xyx^(-1) とすると I_x はH_0 を不変部分空間としてもち、H_0上で行列式が1の直交変換. 写像 φ:U ---> SO(3) ; φ(x) = I_x は全射準同型で Ker φ = {1,-1}. ∴ U/{1,-1} 〜 SO(3). Uは3次元球面 S^3 とみなせるから、このことより、 SO(3)は3次元射影空間 P^3 とみなせることになる。 ♯ この方面にくわしいかたのカキコ期待しますぅ〜。 |
||||||
| 100 | Re:微積分の基本定理の乗法版 | coolee | 1999/11/04 15:18 | HOME | 返信 | |
| > > <問題> 「微積分の基本定理の乗法版」を定式化して、それを証明せよ。
> log→微分→exp という構造なので、 そうですね。微分の乗法版がうまくそうなってることに集約されます。 公式として ・ log f’(x) = (log f(x))' ・ e^f'(x) = (e^f(x))’ とするとバランスがいいかも。ただしここで「’」は乗法版。ちなみに乗法版は太字にするって手を使うと簡便です。 あと微積分の基本定理と言ったら基本定積分公式も含めて言うことが多いようです。 念のため基本定積分公式の乗法版を証明しておくと.. ∫_[a,b] f(x)dx = e^∫_[a,b] log f(x)dx = e^∫_[a,b] (log F(x))'dx = e^[log F(x)]_[a,b] = e^(log F(b) - log F(a)) = e^log(F(b)/F(a)) = F(b)/F(a) = [F(x)]_[a,b]. // 基本定積分公式を使わないで証明するには、基本定積分公式の通常の証明をひとつひとつ几帳面に乗法版にする(たとえば平均値の定理の乗法版とか)必要があります。これは対応関係さえまちがえなければ easyですネ。 |
||||||
| 98 | Re:RE:四則演算 | coolee | 1999/11/03 22:41 | HOME | 返信 | |
| > はじめまして。他の掲示板ではGと名なってます。
ようこそ。 > 足し算、を何回か行うと、掛け算になる。 > 掛け算を何回か行うと、累乗になる。 > 累乗を何回か行うと、、、、、、 > これは概念的には考えれないと思うのですが、 > あまり役にたたないと思われます。 > それは、分配法則や指数法則といった法則がないから。 > なので、大切なのは+と×と、その逆概念のーと÷なので、四則演算という名前があると思います。 たいへん明快です。 あえて食いつくと、 演算法則がなくても重要な構造っていうのがけっこーある、 ぐらいです。 そういう構造でも、演算法則を見出せれば強力な道具になりうるわけですが。 |
||||||
| 97 | RE:四則演算 | G | 1999/11/03 12:41 | 返信 | ||
| はじめまして。他の掲示板ではGと名なってます。
足し算、を何回か行うと、掛け算になる。 掛け算を何回か行うと、累乗になる。 累乗を何回か行うと、、、、、、 これは概念的には考えれないと思うのですが、 あまり役にたたないと思われます。 それは、分配法則や指数法則といった法則がないから。 なので、大切なのは+と×と、その逆概念のーと÷なので、四則演算という名前があると思います。 もっとうまく説明できる方がいれば、教えて。 |
||||||
| 96 | 微積分の基本定理の乗法版 | coolee | 1999/11/03 04:32 | HOME | 返信 | |
| ませまさんのボード(ココ)で次のような問題提起がありました。
問題: 積分の乗法版はあるか?(by G(≠ Dr.Gさん)) G氏自身のコタエ: e^Σlog a_k = Πa_k なので e^∫_[a,b] log f(t)dt が ∫_[a,b] f(t)dt の乗法版(!)。 // G氏はこの概念を ”図形的・実用的に明確にしたい” ということでした。 G氏のこの概念に関して「微積分の基本定理の乗法版」が成り立つことが示せました。 <問題> 「微積分の基本定理の乗法版」を定式化して、それを証明せよ。 |
||||||
| 95 | Re:大モンダイ | coolee | 1999/11/02 00:38 | HOME | 返信 | |
| > <モンダイ> そもそもナンデ四則演算なんでしょう??
<SOL> 集合と集合の比較から差、そして和(=差を足した結果)。 集合の分割および重ねあわせから商、そして積(=商を掛けた結果)。 // ♯ 論理的順序とは逆であることがおもしろい。 |
||||||
| 92 | 大モンダイ | coolee | 1999/10/31 00:50 | HOME | 返信 | |
| <モンダイ> そもそもナンデ四則演算なんでしょう?? | ||||||
| 78 | 一般の角度 | coolee | 1999/10/23 11:10 | HOME | 返信 | |
| 例のn次元角度(近傍の球において占める割合の半径→0での極限)ですが
球面上の緯度Θの点の球面角は「だいたい」わかりました。 赤道に近づくと減少して行きます。 あと1/2予想はほとんど自明に成り立ちます。(錯角の考えで) どういう制約をつければキレイな結果がでるのかなァ・・。(まあ変化を調べるのもおもしろいかもしれませんが。) |
||||||
| 75 | 集合族のモース理論 | coolee | 1999/10/22 14:30 | HOME | 返信 | |
| <もんだい> 「集合族のモース理論」っていうのは可能でしょうか?
集合族Fの台集合S(S⊇∪F)の元xの「高さ」 height x の定義として 何を採用するかが問題ですね。 |
||||||
| 51 | Re:f平均を特徴づける関数 | coolee | 1999/10/18 22:15 | HOME | 返信 | |
| > > ● √[(m - A)^2 + (f(B))^2] + √[(m - B)^2 + (f(A))^2]
> > > > を最小にする m = mf(A,B). // > > <もんだい> この結果をn変数に拡張せよ。 今まで(ナマケぐせから?)n変数のf平均については述べなかったのですが 定義はもちろん次のです。 定義 関数 f:R → R に対して mf:P(f)×P(f)×...×P(f) → R, mf(A,B,...,C) = (Af(A)+Bf(B)+...+Cf(C))/(f(A)+f(B)+...+f(C)) を f平均 とよぶ。 // 例 mx^0(A,B,C) = (A+B+C)/3 mx^(-1/2)(A,B,C) = (A√(BC)+B√(CA)+C√(AB))/(√(BC)+√(CA)+√(AB)) ● mx^0(A,B,C) ≧ mx^(-1/2)(A,B,C). // mx^(-1/2)(A,B,C)は一種の相乗平均と考えていいと思いますが、すくなくともわたしは、目にしたことないです。 |
||||||
| 50 | Re:f平均を特徴づける関数 | coolee | 1999/10/17 22:08 | HOME | 返信 | |
| > ● √[(m - A)^2 + (f(B))^2] + √[(m - B)^2 + (f(A))^2]
> > を最小にする m = mf(A,B). // <もんだい> この結果をn変数に拡張せよ。 |
||||||
| 48 | f平均を特徴づける関数 | coolee | 1999/10/16 07:37 | HOME | 返信 | |
| 定義 関数 f:R → R に対して P(f) = {x∈R| f(x)>0 } とする。
mf:P(f)×P(f) → R, mf(A,B) = (Af(A)+Bf(B))/(f(A)+f(B)) を f平均 とよぶ。 ● f平均は次の平均の公理A1、A2を満たす。 A1. m(A,B) = m(B,A). A2. A ≦ B ⇒ A ≦ m(A,B) ≦ B. (復習終わり) ● √[(m - A)^2 + (f(B))^2] + √[(m - B)^2 + (f(A))^2] を最小にする m = mf(A,B). // |
||||||
| 38 | n進数→数の表示 | 坂田 | 1999/10/12 23:46 | 返信 | ||
| n進数とは…○n^2+○n^1+○+○/n+○/n^2…型表示のことだ考える事ができます。
ここで、n=10とすると、任意の自然数は一意的に有限の位で表わされます。しかし、負の整数を表わそうとするとマイナス記号が必要になり、実数を表わそうとすると無限の位が必要になり(そのときには、0.999…=1.000…と一部だけ一意性がくずれる)、複素数を表わそうとするとプラス記号や虚数単位が必要になります。 また、n=√2とすると、任意の正実数は、割り算の方法によって、一意的に√2進数表示されます。ただし、○印には、整数でなく実数をあてはめることによって。 またn=1とすると、一般的には整数しか表わせないだろうと思われます。 ここでのキーワードは、除法定理、ユークリッド整域などです。 では、n進数→数の表示ということに目を向けましょう。 自然数には、素因数分解という表示があります。素数を使って、2^○×3^○×5^○…型表示することです。○印に負の整数を当てはめる事によって、有理数も2^○×3^○×5^○…型表示することができます。 ここでのキーワードは、初等整数論の基本定理、素元分解整域などです。 また、整数は、3○+8○型表示することも有名な事実です。ここで、3と8は互いに素だというだけで、数字自体に意味はありません。 では、3^○×8^○型表示といったものを考えてみましょう。○印には整数を当てはめるべきだといった感じを掴みとってください。 表示できる数は、有理数の部分集合です。しかし、その有理数の部分集合は稠密です。ですから、任意の実数を表わそうとすると、3^○×8^○型表示の列で表わしうるであろうと思います。ちょうど、無限小数展開(有限小数展開の列)のように。 こうなるといろいろ想像が膨らみますが、実数の連分数展開、実数の連根展開とでもいうべきもの(つまり、ルートの中にルートがあり、その中にルートがあり、といったもの)はきいた事があります。 みなさんは、数の表示という視点で、どのような想像が生まれますか? |
||||||
| 37 | Re:n進数 | 坂田 | 1999/10/12 22:48 | 返信 | ||
| > はじめまして。よろしく。
こちらこそ、よろしく。 > > 4の√2進法表示。 > > 4÷√2=2あまり4-2√2 > > 2÷√2=1あまり2-√2 > > 1÷√2=0あまり1 > > よって4(10進法)=(1)(2-√2)(4-2√2)(√2進法) > 商は整数にするってことですか? 商を実数にすると、割り切れてしまい、あまりの意味がなくなりますので。 > (√2)^4(10進法)=10000(√2進法) でわ? その通りです。僕の間違いです。 > 2/3(10進法)=0.101010…(2進法) っていうような変換 > は坂田さんはどういうふうにやってますか。 この場合は、0.101010…(2進法)=1/2+1/8+1/32+…と等比級数として計算しましたが。2/3(10進法)を2進法に変換するには? まず、1の位は0です。小数点の位を求めるのに、例えば2^3倍した数を考えます。 (2^3×2/3)÷2=2あまり4/3 2÷2=1あまり0 1÷2=0あまり1 よって(2^3×2/3)=101.…、これの位をずらして2/3=0.101… > > しかし、しかし、どう考えてもe^iα、たとえば(1+i)/2進数が考える事ができません。いいお知恵をお貸しください。 > e^iαはe^(iα)ですか? > だとすると(1+i)/2はe^(iα)とは書けないですね。 すいません。単なる書き間違いです。 |
||||||
| 35 | 続・平均曲面 z = m_f (x,y) | coolee | 1999/10/12 18:21 | HOME | 返信 | |
| 曲面 z = m_f (x,y) の形状を微分幾何学的に調べてみるのもおもしろいと思います。
● f(x)=x^k,a^x(a>0)のとき、曲面 z = m_f (x,y) は線織面(ruled surface)である。 (∵) 次の公式より。 mx^k(x,cx) = (c^(k+1) + 1)x/(c^k + 1). ma^x(x,x+c) = x + ca^c/(1 + a^c). // |
||||||
| 34 | Re:n進数 | coolee | 1999/10/12 13:03 | HOME | 返信 | |
| > 突然の投稿をお許しくださいませ。
はじめまして。よろしく。 > n進数の表示の一意性の元となるものに、割り算の一意性があります。 > a÷b=cあまりd(ただし|d|<|b|)となるものです。これをもとにすると。 > -- 途中省略 -- > 4の√2進法表示。 > 4÷√2=2あまり4-2√2 > 2÷√2=1あまり2-√2 > 1÷√2=0あまり1 > よって4(10進法)=(1)(2-√2)(4-2√2)(√2進法) > ここで、4(10進法)=(√2)^4(10進法)=40000(√2進法)としたいとこですが、一意性を優先した方がいいと思います。 商は整数にするってことですか? (√2)^4(10進法)=10000(√2進法) でわ? > ここまではうまくいきますが、次からが考えどころです。 > 3の1進法表示。割り算の一意性を少し修正して。 > 3÷1=2あまり1 > 2÷1=1あまり1 > 1÷1=0あまり1 > よって3(10進法)=111(1進法) 527(10進法)=(5)(1)(17)(10進法) ってカンジですね。 > 5の1/2進法表示。割り算ではうまくいかないので。 > 5(10進法)=101(2進法)=1.01(1/2進法) > しかしこうすると、2/3(10進法)=0.101010…(2進法)=…0101010(1/2進法)てなことが起こります。 2/3(10進法)=0.101010…(2進法) っていうような変換 は坂田さんはどういうふうにやってますか。 > しかし、しかし、どう考えてもe^iα、たとえば(1+i)/2進数が考える事ができません。いいお知恵をお貸しください。 e^iαはe^(iα)ですか? だとすると(1+i)/2はe^(iα)とは書けないですね。 ♯ 皆さんの(議論のための議論ではない)意欲的な投稿を期待します。 |
||||||
| 33 | n進数 | 坂田 | 1999/10/12 00:51 | 返信 | ||
| 突然の投稿をお許しくださいませ。
n進数の表示の一意性の元となるものに、割り算の一意性があります。 a÷b=cあまりd(ただし|d|<|b|)となるものです。これをもとにすると。 23の10進法表示。 23÷10=2あまり3 2÷10=0あまり2 よって23(10進法)=23(10進法) 5の2進法表示。 5÷2=2あまり1 2÷2=1あまり0 1÷2=0あまり1 よって5(10進法)=101(2進法) 4の√2進法表示。 4÷√2=2あまり4-2√2 2÷√2=1あまり2-√2 1÷√2=0あまり1 よって4(10進法)=(1)(2-√2)(4-2√2)(√2進法) ここで、4(10進法)=(√2)^4(10進法)=40000(√2進法)としたいとこですが、一意性を優先した方がいいと思います。 5の-2進法表示。 5÷(-2)=-2あまり1 -2÷(-2)=1あまり0 1÷(-2)=0あまり1 よって5(10進法)=101(-2進法) 5の2i進法表示。 5÷(2i)=-2iあまり1 -2i÷(2i)=-1あまり0 -1÷(2i)=0あまり-1 よって5(10進法)=(-1)(0)(1)(2i進法) ここではあまりを-1,0,1としましたが、0,1.2に限定する事にすると、変形2i進数表示ができます。 ここまではうまくいきますが、次からが考えどころです。 3の1進法表示。割り算の一意性を少し修正して。 3÷1=2あまり1 2÷1=1あまり1 1÷1=0あまり1 よって3(10進法)=111(1進法) 5の1/2進法表示。割り算ではうまくいかないので。 5(10進法)=101(2進法)=1.01(1/2進法) しかしこうすると、2/3(10進法)=0.101010…(2進法)=…0101010(1/2進法)てなことが起こります。 しかし、しかし、どう考えてもe^iα、たとえば(1+i)/2進数が考える事ができません。いいお知恵をお貸しください。 |
||||||