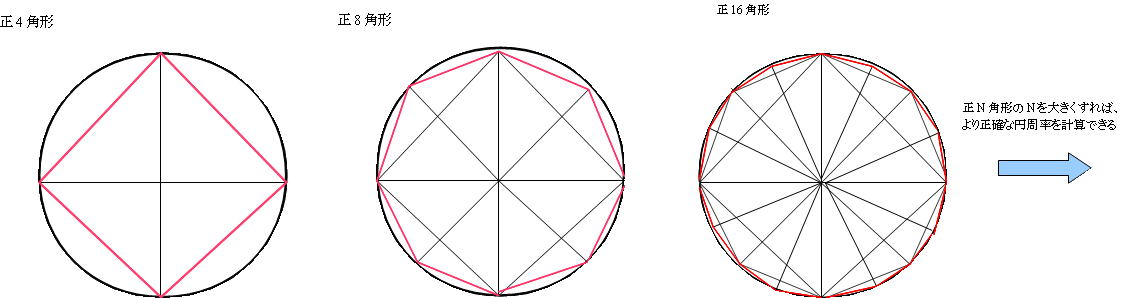
円周率の最も基本的な算出方法は、円に内接する 正N角形(Nは2の階乗)の辺から算出する方法です。Nを大きくしていき疑似的に円周に近似させ、円周率を計算するというものです。
正N角形の円に接する辺の長さは、三平方の定理を用いて計算することができます。
1. 円周率を 円に内接する正N角形の辺から算出
円周率の最も基本的な算出方法は、円に内接する 正N角形(Nは2の階乗)の辺から算出する方法です。Nを大きくしていき疑似的に円周に近似させ、円周率を計算するというものです。
正N角形の円に接する辺の長さは、三平方の定理を用いて計算することができます。

2. 円周率計算の考え方
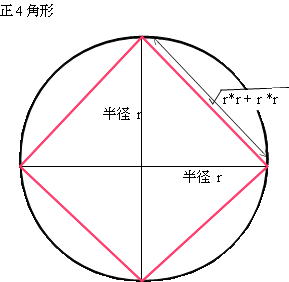
(1) 正4角形の場合の円に接する三角形の斜辺の長さ
三平方の定理から正4角形の場合の円に接する辺の長さを算出します。
(2) 正N角形の円に接する三角形の斜辺の長さ
正N角形の円に接する辺と、正N/2角形の辺との関係を調べます。
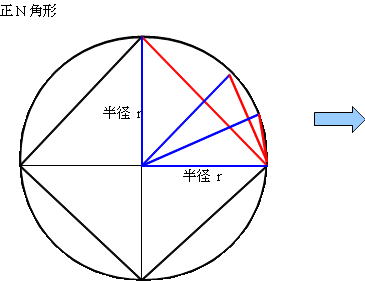
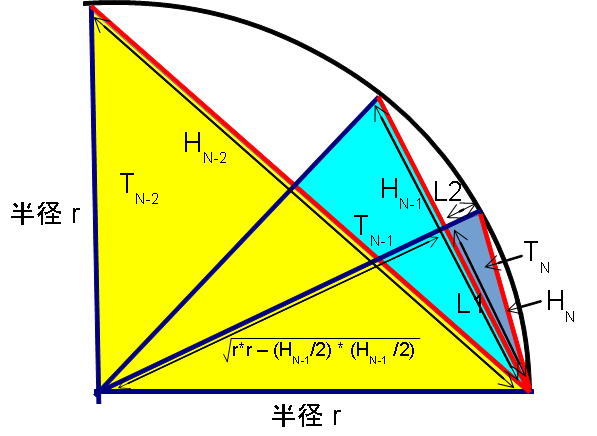
青色の線: 半径
赤色の線: HN、HN-1、HN-2はそれぞれ直角三角形 TN、TN-1、TN-2の斜辺

3. 円周率を求めるプログラム
上記の関係式から以下の円周率を求めるプログラムが作成できます。Prologで書いています。
プログラムのダウンロード
ダウンロードして、SWI-Prolog等のPrologのコンパイラでコンパイルすれば、実行できます。
直径100の円で正64角形での辺の長さを求めたい場合、
inside_pi( 64, 100, Hypotenuse ).
実行結果は
64 3.140331156954753
Hypotenuse = 4.906767432741801
Hypotenuse は斜辺の長さです。 図では、HNを指します。
(これは、LPA-Prologでの結果です。)

このプログラムはLPA PrologとSWI-Prologで動きました。
LPA Prologは市販品(有料)ですが、28日間のFree Trialができます。 Free Trial 時には多少の制限があるみたいです。
SWI-Prologはフリーソフトです。
計算結果ですが、処理系の計算結果の丸めにより、処理系により計算結果が微妙に違ってくることが想定されます。
LPA Prolog 5.0 で直径が1の円の場合での計算結果は以下となります。
学校で習った円周率3.14は正64角形で円周率を求めた場合です。
通常の処理系の有効桁計算では、正134217728角形でほぼ円周率は収束していきます。
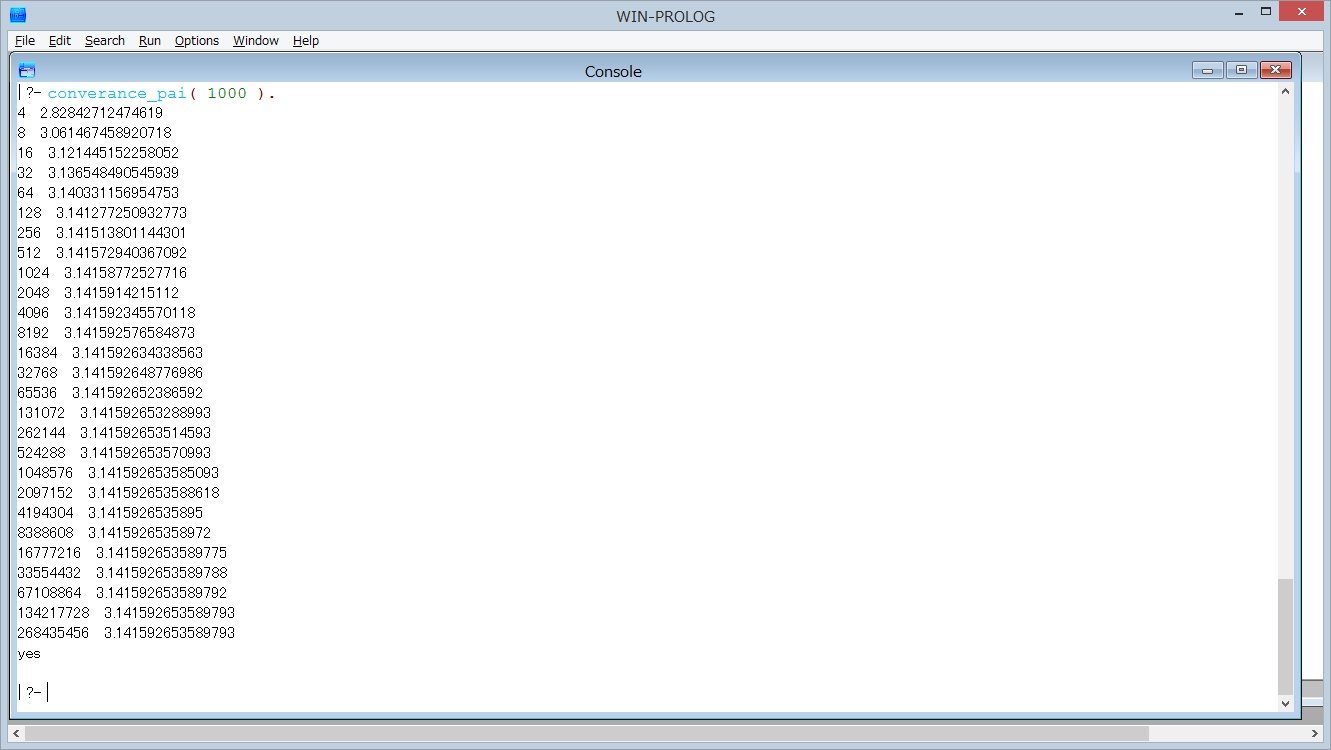
| 正N角形 | 正N角形の辺の長さ Pi 円周率近似 |
| 4 | 2.82842712474619 |
| 8 | 3.061467458920718 |
| 16 | 3.121445152258052 |
| 32 | 3.136548490545939 |
| 64 | 3.140331156954753 |
| 128 | 3.141277250932773 |
| 256 | 3.141513801144301 |
| 512 | 3.141572940367091 |
| 1024 | 3.14158772527716 |
| 2048 | 3.1415914215112 |
| 4096 | 3.141592345570118 |
| 8192 | 3.141592576584872 |
| 16384 | 3.141592634338563 |
| 32768 | 3.141592648776986 |
| 65536 | 3.141592652386591 |
| 131072 | 3.141592653288992 |
| 262144 | 3.141592653514593 |
| 524288 | 3.141592653570993 |
| 1048576 | 3.141592653585093 |
| 2097152 | 3.141592653588618 |
| 4194304 | 3.141592653589499 |
| 8388608 | 3.141592653589719 |
| 16777216 | 3.141592653589774 |
| 33554432 | 3.141592653589788 |
| 67108864 | 3.141592653589792 |
| 134217728 | 3.141592653589793 |
| 268435456 | 3.141592653589793 |
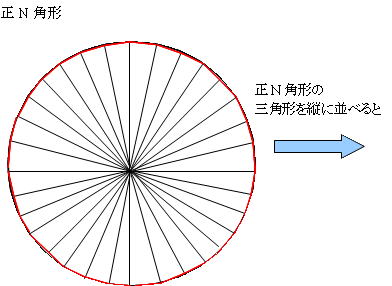
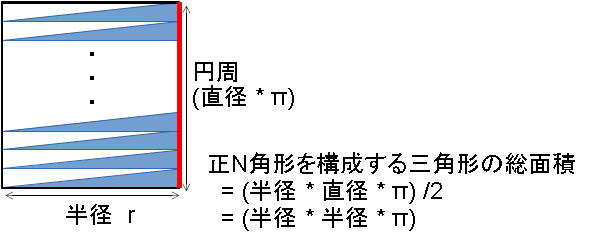
4. 面積計算の考え方
円の面積を求める基本的な方法は、円周率と同様に、正N角形を作り、正N角形の面積を計算し、近似的に円の面積を求めるというものです。
正N角形と正N/2角形を構成する三角形の関係から、正N角形の面積を計算します。
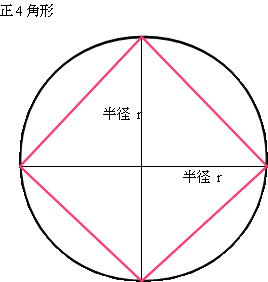
(1) 正4角形の場合の円に接する三角形の面積
三角形の面積は 底辺 * 高さ / 2ですが、
円に接する正4角形の場合、三角形の面積は 半径 * 半径 / 2
(2) 正N角形の場合の円に接する三角形の面積
正N角形を構成する三角形の面積と、正N/2角形を構成する三角形の関係を調べます。
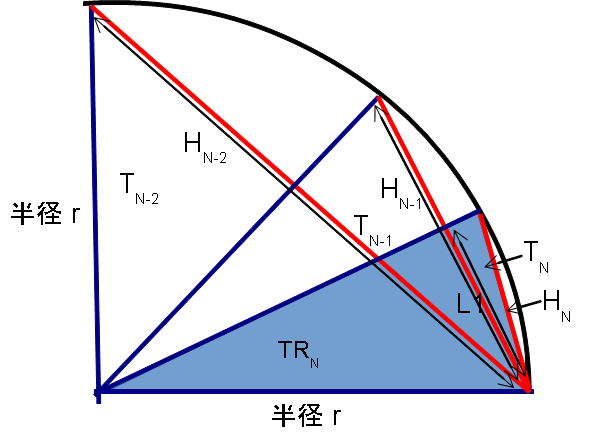
正N角形を構成する三角形TRの面積は
三角形の面積 底辺 * 高さ / 2より
・ 三角形TRの面積 は (r * (HN-1)/2)/2
5. 面積を求めるプログラム
上記の関係式から以下の面積を計算するプログラムが作成できます。三角形の円周率を求めるプログラムの関数も三角形の高さを求めるために利用します。
プログラムのダウンロード

円の直径を2で計算した場合の計算結果は以下となります。
公式では直径2の場合は面積は 半径 * 半径 * πで
3. 1415926535 8979323846・・
となります。
正N角形のNを大きくしていく計算結果でも、公式で計算した値に収束していることが確認できます。
| 正N角形 | 正N角形の面積(直径2の場合) |
| 4 | 2 |
| 8 | 2.82842712474619 |
| 16 | 3.061467458920718 |
| 32 | 3.121445152258052 |
| 64 | 3.136548490545939 |
| 128 | 3.140331156954753 |
| 256 | 3.141277250932773 |
| 512 | 3.141513801144301 |
| 1024 | 3.141572940367091 |
| 2048 | 3.14158772527716 |
| 4096 | 3.1415914215112 |
| 8192 | 3.141592345570118 |
| 16384 | 3.141592576584872 |
| 32768 | 3.141592634338563 |
| 65536 | 3.141592648776986 |
| 131072 | 3.141592652386591 |
| 262144 | 3.141592653288992 |
| 524288 | 3.141592653514593 |
| 1048576 | 3.141592653570993 |
| 2097152 | 3.141592653585093 |
| 4194304 | 3.141592653588618 |
| 8388608 | 3.141592653589499 |
| 16777216 | 3.141592653589719 |
| 33554432 | 3.141592653589774 |
| 67108864 | 3.141592653589788 |
| 134217728 | 3.141592653589792 |
| 268435456 | 3.141592653589793 |
| 536870912 | 3.141592653589793 |
円の面積の公式
半径 * 半径 * π
イメージとしては、こんな感じではないでしょうか?
6. Prologの開発環境
実際のProlog開発で使用する環境は、プログラム作成を行いやすくしています。
Prologでの作業がイメージできるように LPA PrologとSWI-Prologの画面を貼り付けます。
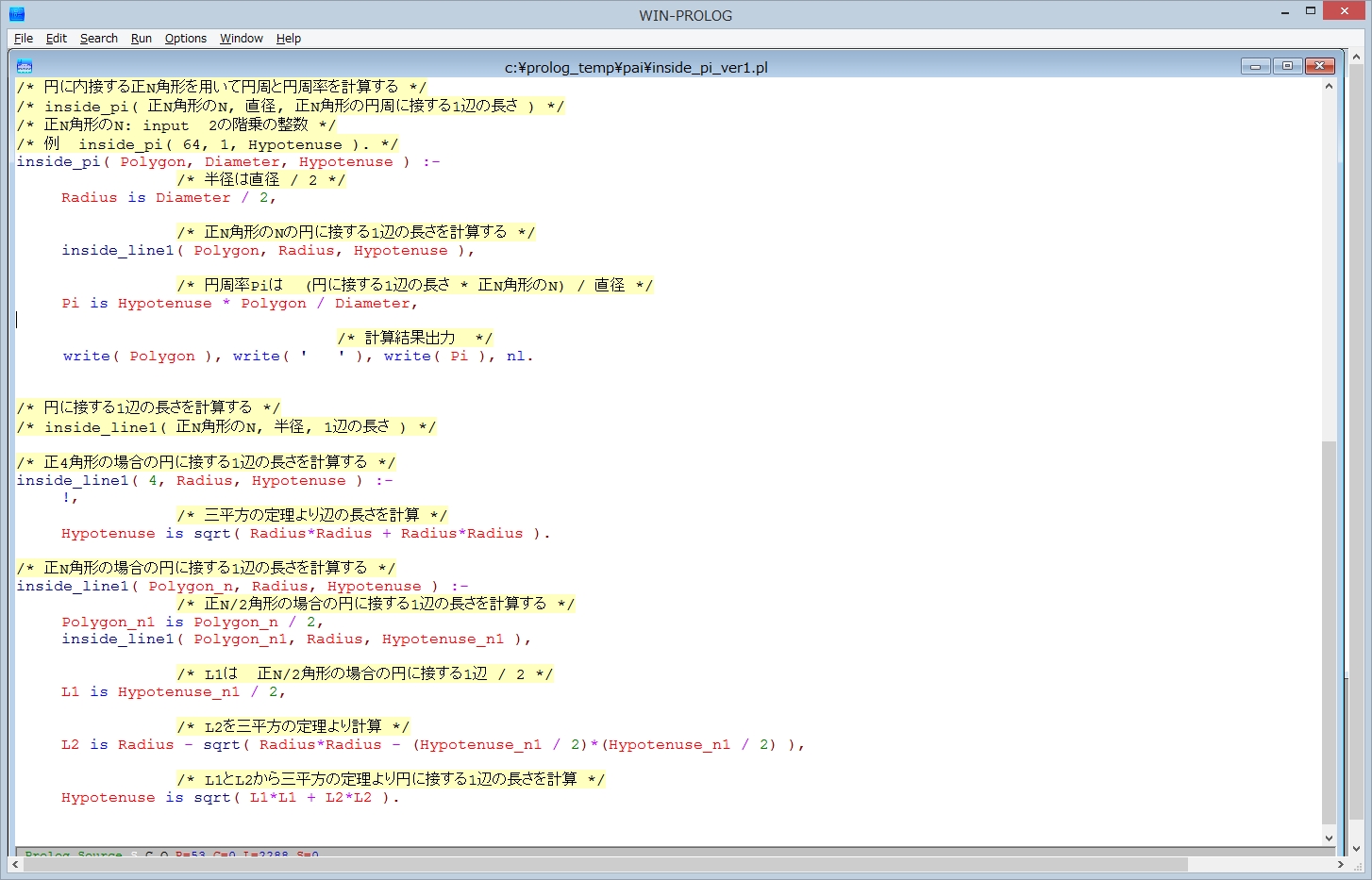
(1) LPA Prologの場合、
① エディタ画面
② LPA Prologで、コンパイルし、直径 1000 で 正N角形と正N/2角形の円周率の差が0.0000000000000001以下となるまで計算させた結果は
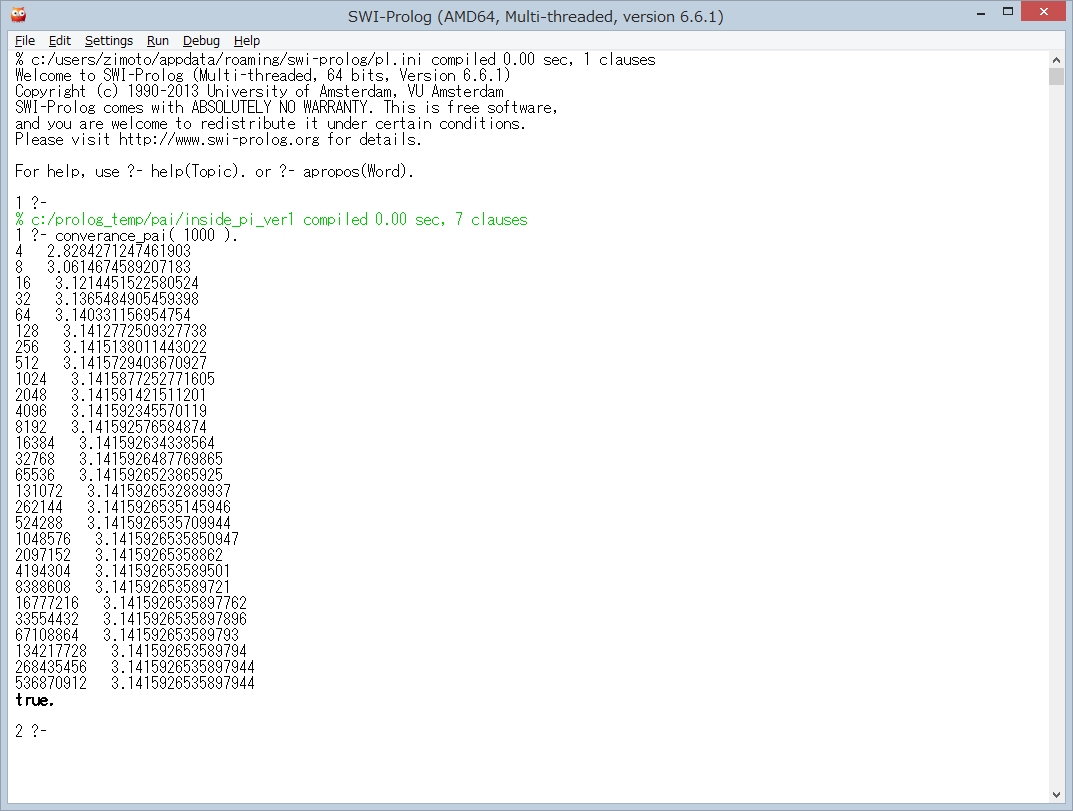
(2) SWI-Prologの場合
フリーウェアなので、通常はこちらの方が利用しやすいと思います。もう少し、マニュアルが解りやすければ良いのですが。
① エディタ画面
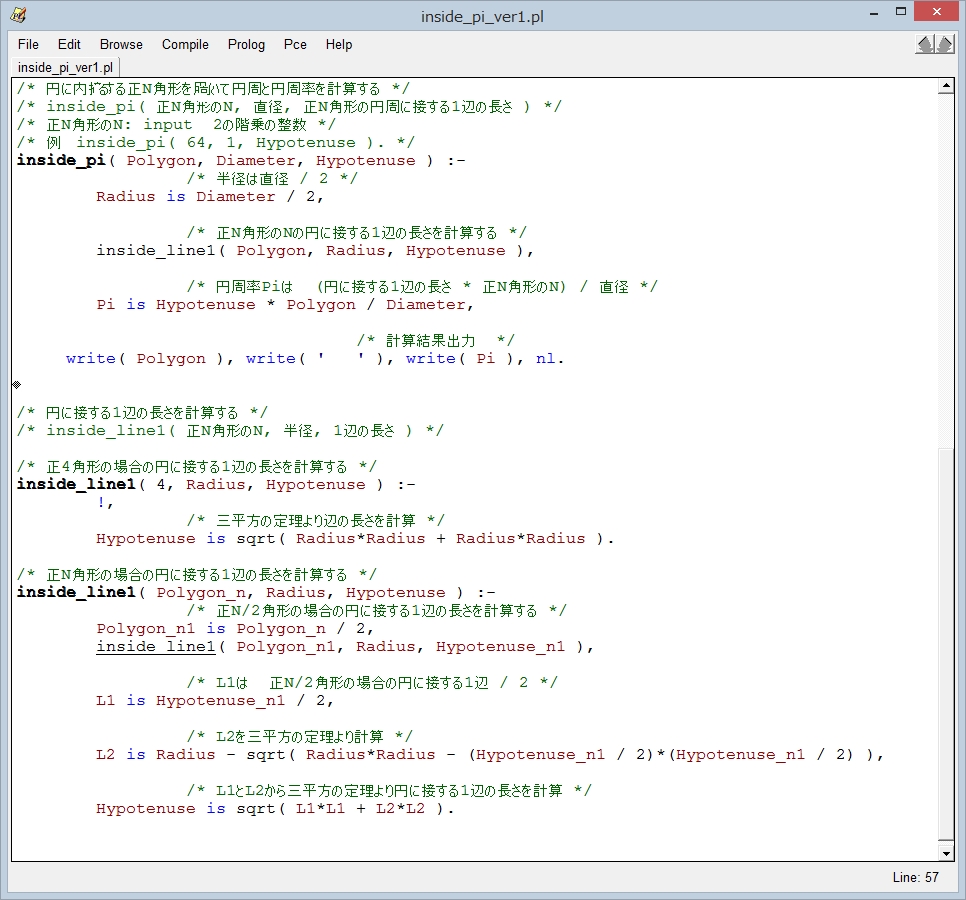
② SWI-Prologでコンパイルし、直径 1000 で 正N角形と正N/2角形の円周率の差が0.0000000000000001以下となるまで計算させた結果は