トップページ > フーリエ変換入門(FFT入門) > フーリエ変換(2)
前回は, フーリエ級数で表す対象を「周期2πの周期関数」から 「任意の周期2Lの周期関数」として,制限をやわらげました。 しかし,あくまで「周期関数」であることには変わりません。 そして,実用上きれいな周期関数を相手にすることなんて滅多にありません。 そこで,今回は周期を無視していわゆる「非周期関数」を扱えるように拡張します。

ある周期2Lだった関数を上図のように限りなく引き伸ばして,「周期が無限の関数だ」と見るようにします。 なんだか不思議な感じですが,一応理屈の上では「周期関数」でありながら,実質「非周期関数」というか, 「孤立波形」のような物を扱う状態となります。 これから前ページと同じ流れで周期をL→∞と変化させるわけですが, いきなり極限操作をしても分かりづらいので,1つ1つ式変形をしていくことにします。
まず,周期2Lのフーリエ級数・フーリエ係数は以下のような感じでした。簡単のために複素形式で書いています。
(※なお,ckを計算する式の積分変数は,区別がつくように“x”ではなく“t”としています。)
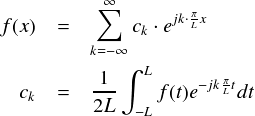
ここで,角周波数に相当する“k・π/L”は,周期2πの場合と一般化した周期2Lの場合とで,以下のような対応関係になっています。
| 周期2π | 周期2L | |
| 角周波数 | k | k・2π/2L = k・π/L |
上記2つの角周波数で異なる点は,周期2πの場合は角周波数が“k”という整数であらわされるのに対して, 周期が2Lになると“π/L”との積を取っているため角周波数は整数ではなくなります。 Lの値が大きくなると,より細かい角周波数まで表せるようになる感じです。 (※そもそも,“π/L”という項は,元々の周期2πの関数においてxが-π〜πの範囲で1周期だったものを, 周期2Lの場合ではxが-L〜Lの範囲で動くので,それを元の-π〜πに直すために付いている係数でした。)
しかし,いずれの場合も「あるk番目の角周波数」を表していることには変わらないので, 分かりやすくするために以下のように変数を置き換えておきます。
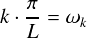
“ω”の添え字の“k”は,「k番目の角周波数」という気持ちを表しています。 すると,角周波数の“ω”が変化する最小単位は式からすぐ分かる通り,“π/L”だということになります。 この「“ω”の最小単位」を,とりあえず“Δω”と書くことにします。
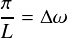
| 周期2π | 周期2L | 周期∞ | |
| 角周波数の単位量 | 1 | Δω = π/L | dω |
もともと周期2πの関数をフーリエ級数展開する場合,角周波数の単位量というのは,“1”なのでした。 sin(x),sin(2x),・・・という感じで,整数の周波数のみを考えれば十分でした。 しかし今回のように,“L→∞”としてどんどんLを大きくしていった場合, どんどんΔωの値は小さくなります。つまり,角周波数は連続量になるということが分かります。 これだと,従来のように「k番目の周波数のフーリエ係数はckだ」と言うことができません。 連続量なのに,「k番目」などという(離散的な)言い方はナンセンスです。
これまでの話で,周期が無限になった場合は連続した値の角周波数を考えないとフーリエ級数を表せないことが分かりました。 またそれに伴い,「k番目のフーリエ係数ck」という言い方は少々ナンセンスでもあります。 後から“L→∞”とした場合に“ck”という文字が残っているのも変なので,“ck”の部分には計算式自体を代入してしまうことにします。
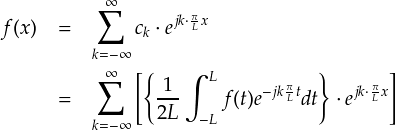
ここで,先ほど出てきた“ω”を使って書きなおしてみます。
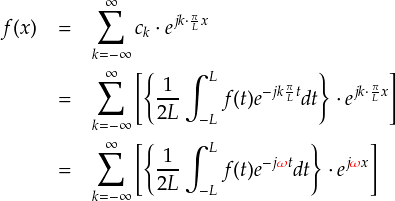
更に,“1/L”の部分は,“Δω”の定義より次のように書き換えることができます。
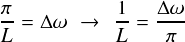
すると,元の式は次のように変形できます。
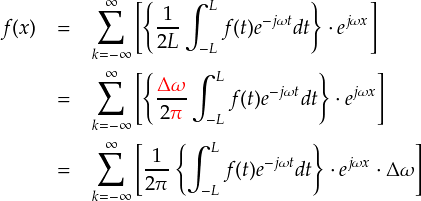
最後に,“L→∞”の極限操作を行います。 すると,“Δω”→“dω”となり,またシグマの部分はdωによる積分に書き換えることができます。 (※途中,リーマン積分の形が見やすいように“Δω”を“k/L”と書き直しています)
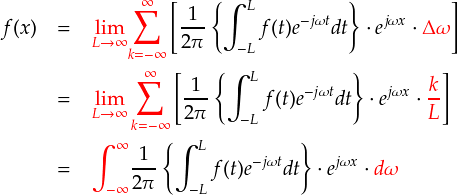
ここまでの結果を整理すると,以下の式となります。
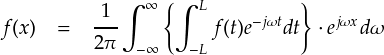
上の式は,「フーリエの積分定理」と呼ばれているそうです。 この式まで来れば,もうフーリエ変換を導出したも同然なのですが,今回は極限操作でごちゃごちゃといろいろ計算したので一度切ります。 次回は,この式の解釈を含めて,「フーリエ変換」の話になります。