問題ゼミナール 2
[06](表示式)
[07](面積ベクトル)
[08](包除原理)
[09](合同式)
[10](不変量)
06|07|08|09|10

[6](表示式)
数列 1,2,2,3,3,3,4,4,4,4,5,・・・・・の一般項 f(n) を与える(閉じた)表示式 を求めよ。
<Sol> g(k)を f(n)=k となる最初の番号nとすると
g(k) = 1+ Σi=1k-1 i = 1+ k(k-1)/2.
また f(n) = k ⇔ g(k) ≦ n < g(k + 1)
⇔ (k- 1/2)2 ≦ 2n - 7/4 < (k+ 1/2)2
⇔ √(2n - 7/4) - 1/2 < k ≦ √(2n - 7/4) + 1/2.
よって f(n) = [ √(2n - 7/4) + 1/2 ]. //
[類題]
方程式 |x+|y|+1| + |x-|y|-1| = 2 が表す図形をもとめよ。
<Sol> 答え: 点(-1,0)と点(1,0)を結ぶ線分。
(∵)左辺L = |(x+|y|+1)| + |(x-|y|-1)| = |x+α| + |x-α| (α≧1)
|(x+α)-(x-α)| ≦ L ∴ |2α| ≦ 2 ∴ |α| = ||y|+1| ≦ 1 ∴ y = 0
∴ L = |x+1| + |x-1| = 2. このとき |(x+1)+(x-1)| ≦ 2 ∴ -1 ≦ x ≦ 1
逆に -1≦ x ≦1 のとき L = 2. //
♯ L1 = {(x,y)|y=0} = V(y)
♯ L2 = {(x,y)|-1≦x} = V(x+1-|x+1|)
♯ L3 = {(x,y)|x≦1} = V(x-1+|x-1|) (但し V(*)の * は定義多項式)
♯ とすると 点(-1,0)と点(1,0)を結ぶ線分 = L1 ∩ L2 ∩ L3
♯ よって |y| + |x+1-|x+1|| + |x-1+|x-1|| = 0 も同じ線分を表す。
【 NOTE 】 一般に V(f)∩V(g) = V( |f|+|g| ) はよく知られているが、それを補う公式
V(f) ∪ V(g) = V( |f+g| - |f-g| )
が成り立つ。(NITRO_1 の公式)
練習問題: NITRO_1 の公式を証明せよ。
<Sol> 左辺 L ,右辺 R とする。L⊆R は容易に示される。
L⊇R; P∈R とする。
P ∈ V( ( |f+g| - |f-g| ) ( |f+g| + |f-g| ) )
= V( |f+g|2 - |f-g|2 )
= V( 4fg )
= V( fg )
= V(f) ∪ V(g)
∴ P∈L. //
等式 Σj=0nΣi=0j f(i,j) = Σi=0nΣj=in f(i,j) を示せ。
また、格子を使って説明せよ。
<Sol> いとわずに書き下してみればよい。
格子点
(0,n)(1,n)(2,n)・・(n,n)
・・・・・・・・・・
・・・・・・・・・
(0,2)(1,2)(2,2)
(0,1)(1,1)
(0,0)
に対して左辺はタテに右辺はヨコに寄せ集めてる。 //
練習問題: 和 Σj=0nΣi=jn nCi iCj を求めよ。
<Sol> (与式) = Σi=0nΣj=0i nCi iCj
= Σi=0n ( nCiΣj=0i iCj )
= Σi=0n nCi( 1 + 1 )i
= Σi=0n nCi 2i
= ( 1 + 2 )n
= 3n //
演算 +,×,÷ を演算 − と逆数をとることから導け。
<Sol> u + v = u - (0 - v)
1/(1 - x) - 1/(0 - x) = 1/(x - x2) より x - x2 を求められる。
x - (x - x2) = x2
(x - y)2 - x2 - y2 = -2xy
また 1/((0 - 1/u) - 1/u) = - u/2. よって xy も求められる。
x ÷ y は x × (1/y) として求められる。 //

[7](面積ベクトル)
四面体の各面の外向きの面積ベクトルの和は0であることを示せ。
<Sol> 四面体を P1P2P3P4 とし、Pi の対面の外向きの面積ベクトルをSi とする。
また、ベクトルP4Pj(j = 1,2,3)を rj とする。 r1、r2、r3 は右手系とする。
S4 = (1/2) (P1P2 × P1P3)
= (1/2) (r2 - r1)×(r3 - r1)
= -S1 -S2 -S3
∴ S1 + S2 + S3 + S4 = 0. //
研究課題: 一般の多面体でも成立することを示せ。
研究課題: 高次元に拡張せよ。
<Sol(概略)> 4次元の場合について。(一般の「n次元外積」については
数学2の記事(268)(ココ)を参照)
S5 = (1/3!) (P1P2 × P1P3 × P1P4)
= (1/3!) (r2 - r1) × (r3 - r1) × (r4 - r1)
= (1/3!) (r2×r3×r4 + r1×r2×r4 + r3×r1×r4 + r2×r1×r3)
= -S1 -S3 -S2 -S4
∴ S1 + S2 + S3 + S4 + S5 = 0. //
練習問題: 2次元の場合について確かめよ。
研究課題: ある種の多面体が「閉じている」ことを面積ベクトルの和で特徴づけよ。

[8](包除原理)
等式 n ! = Σk=0n-1 (-1)knCk(n-k)n を証明せよ。
<Sol> | {全射 f: [n]→[k]} | を σ(n,k) で表示する。( [k]:= {1,2,...,k} )
σ(n,k) = Σi=0k (-1)ikCi (k-i)n を示せばよい。
以下 補集合は全体集合 Ω = {f: [n]→[k]} におけるものとする。
i∈[k] について Si = |{f∈Ω| i∈ [k] - f([n])}| とする。
σ(n,k) = |∩i∈[k] Sic| = Σ[k]⊇J (-1)|J| |∩j∈J Sj|
|J| = i のとき ∩j∈J Sj = {f: [n]→ [k] - J} なので
|∩j∈J Sj| = (k-i)n
∴σ(n,k) = Σi=0k (-1)ikCi (k-i)n . //
[類題]
(1)正の整数 a1, a2, ... , an に対して
max( ai: i∈[n] ) = Σ[n]⊇I≠φ (-1)|I|-1 min( ai: i∈I )
が成り立つことを示しなさい。
(2)正の実数に対しても成り立つことを示しなさい。
[類題]
n人宛ての手紙と封筒とを無作為に組み合せるときどの手紙も正しい封筒に
入らない確率σnとすると lim σn = 1/e となることを示せ。
<略解> [n]上の置換で不動点をもたないもの(全換置換)の総数を D(n) とする。
[n]上の置換σで σ(i) = i (i が不動点)であるのの全体を Pi で表示する。
D(n) = | ∩i∈[n] Pic | = Σ[n]⊇J (-1)|J| | ∩j∈J Pj |
= ... = n!(Σk=0n (-1)k・1/k!)
これより題意の等式をえる。 //

[9](合同式)
平面上の4点でどの2点間のキョリもodd(奇数)なのは存在しないことを示せ。
<Sol> 題意をみたす4点z1,z2,z3,z4があるとする。
四面体z1z2z3z4の体積Vについて ziとzjのキョリを dij とすると
V 2 = (1/288) D = 0.
但し Dの (i,j) 成分は i = j のとき 0
i ≠ j のときは i も j も4以下なら dij、そうでないなら 1. (四面体のヘロンの公式)
また任意の奇数2n+1について (2n + 1) 2 ≡ 1 (mod 8).
よって
| 0 1 1 1 1 |
| 1 0 1 1 1 |
| 1 1 0 1 1 | ≡ 0 (mod 8).
| 1 1 1 0 1 |
| 1 1 1 1 0 |
しかし左辺の行列式の値は4で矛盾。 よって存在しない。 //
【 NOTE 】 解の中の行列式をスマートに計算すると
|0 1 1 1 1| |0 1 1 1 1 1| |-1 0 0 0 0 1| |-1 0 0 0 0 1|
|1 0 1 1 1| |1 0 1 1 1 1| | 0 -1 0 0 0 1| |0 -1 0 0 0 1|
|1 1 0 1 1| =|1 1 0 1 1 1| =| 0 0 -1 0 0 1| =|0 0 -1 0 0 1| = 4.
|1 1 1 0 1| |1 1 1 0 1 1| | 0 0 0 -1 0 1| |0 0 0 -1 0 1|
|1 1 1 1 0| |1 1 1 1 0 1| | 0 0 0 0 -1 1| |0 0 0 0 -1 1|
|0 0 0 0 0 1| |-1 -1 -1 -1 -1 1| |0 0 0 0 0 -4|
一般に次が成り立つ。
練習問題: 次の等式を証明せよ。
|x1 a a a|
|b x2 a a|
|b b x3 a| = Πν=1n (xν-a) + aΣi=1n (Πν=1i-1(xν-a)Πν=i+1n(xν-b))
|...........|
|b b b xn|
<Sol>一般に、A = (aij) での (i,j)余因子をΔijとすると、
| |x1 |
| | |
| A | |
| | | = |A|z - Σi,j=1n Δijxiyj
| |xn |
|-----------------+---|
|y1y2 yn | z |
が成り立つ。(∵ n+1 列で展開してから n 行で展開)
∴ (与式の左辺)= |x1 a ... a 0|
|b x2 ... a 0|
| ........... |
|b b ... xn 0|
|1 1 ... 1 1|
|x1-a 0 0 .... 0 | -a |
|b-x2 x2-a 0 .... 0 | -a |
= | 0 b-x3 x3-a .. 0 | -a |
| .................. | |
| 0 0 0 .. xn-a| -a |
|--------------------+----|
| 0 0 0 .... 1 | 1 |
= |A|・1 - Σi=1n (-a)・1
= Πν=1n (xν-a) + aΣi=1n {(-1)i+nΠν=1i-1(xν-a)Πν=i+1n(b-xν)}
= (与式の右辺). //
【 NOTE 】 四面体のヘロンの公式はオイラーによる。 n次元への拡張もされている。
練習問題: 四面体のヘロンの公式を証明せよ。
<略解> 四面体 ABCO とし、ベクトル BC,CA,AB,OA,OB,OC を a,b,c,p,q,r
とする。
p,q、r は右手系になっているものとする。
四面体から決まる平行6面体を考えることにより、
6V = p×q・r
このことから、O を原点とする右手座標系をかんがえると、
6V = |p q r| = | t[p q r] |
| p・p p・q p・r |
∴ 36V2 = | q・p q・q q・r |
| r・p r・q r・r |
p・p = |p|2, q・r = (|q|2 - |r|2 - |a|2)/2 などに注意して式変形すると
求める公式を得る。 //
[類題]
かってな整数 a, b, c に対して n3 + a n2 + b n + c が非平方数
となるような自然数 n が存在することを示せ。(パトナム問題)
<Sol> n = 1, 2, 3, 4 に対して f(n) = n3 + a n2 + b n + c が平方数とする。
平方数は ≡ 0 または ≡ 1 (mod 4) である。
f(2) - f(4) ≡ 2b (mod 4) ゆえもし f(2) も f(4) も平方数とすると 2b ≡ 0 (mod 4).
一方 f(3) - f(1) ≡ 2b + 2 (mod 4) ゆえもし f(1) も f(3) も平方数とすると
2b + 2 ≡ 0 (mod 4). これは矛盾。 //
[類題]
33334444 + 44443333 は7の倍数であることを示しなさい。
<Sol> 3333 ≡ 1 (mod 7) , 4444 ≡ -1 (mod 7) である。
∴ 33334444 + 44443333 ≡ 14444 + (-1)3333 = 1 - 1 = 0 (mod 7). //
[類題]
44444444 の各桁の数の和をA、Aの各桁の数の和をBとする。
Bの各桁の数の和を求めよ。(数学オリンピック)
<Sol> N = 44444444 とする。
N<(104)4444 = 1017776 より、Nのケタ数は17776以下。
A≦17776×9 = 159984 ∴ B≦6×9 = 54
54以下の正整数で各桁の数の和が最大なのは49で、その値は13.
よって、求める数をCとすると、C≦13.
一般に、 an10n + ... + a0 ≡ an + ... + a0 (mod 9)
なので、N≡A≡B≡C.
また
N ≡ 74444 (∵ 4444 ≡ 7)
= 73×1481×7
≡ 7 (∵ 73 ≡ 1)
∴ C≡7 かつ C≦13. よって、 C = 7. //
[類題]
k が奇数であるとき、
1k + 2k + ... + nk は 1 + 2 + ... + n で割り切れることを示せ。
<Sol> 1 + 2 + ... + n = n(n+1)/2 なので
2(1k + 2k + ... + nk) が n(n+1) で割り切れることを示せばよい。
mod n で、
2(1k + 2k + ... + nk) ≡ 2(1k + 2k + ... + (n-1)k)
= (1k+(n-1)k) + (2k+(n-2)k) + ... + ((n-1)k+(n-(n-1))k)
≡ (1k+(-1)k) + (2k+(-2)k) + ... + ((n-1)k+(-(n-1))k)
= 0
mod (n+1) で、
2(1k + 2k + ... + nk) = (1k+nk) + (2k+(n-1)k) + ... + (nk+1k)
≡ 0
n と n+1 は互いに素ゆえ、
2(1k + 2k + ... + nk) は n(n+1) で割り切れる。 //

[10](不変量)
2つのレジスタ(数値を保存し、演算のできるシステム)0、1があり、
命令Aij、Bij(i,j = 0,1 ; i ≠ j)は
Aij:レジスタiの内容をjの内容に足し、iはそのままにする
Bij:レジスタiの内容をjの内容から引き、iはそのままにする
とする。
これらの命令だけでは0と1の内容を(一般には)交換できないことを示せ。
<Sol> 交換の表現行列は
( 0 1 )
( 1 0 )
で行列式は -1である。 一方、命令Aij、Bijの表現行列の行列式は 1.
よって、一般には交換できない。 //
[類題]
零環でない可換環 R に対して、Rm 〜 Rn ならば m = n であることを示せ。
<Sol> m > n とする。
φA: Rm → Rn,φB: Rn → Rm を R 上の行列 A ,B による互いに逆な同型写像とする。
m 次正方行列 A* ,B* を
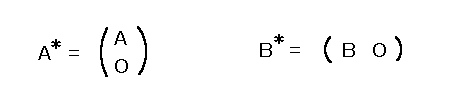
と定義すると、B*A* = Im (m 次単位行列)であるから det(B*)det(A*) = 1.
しかしこのようなことはありえない。よって m ≦ n.
同様にして n ≦ m なので m = n を得る。 //
[類題]
カメレオン45匹中 13匹は灰色、15匹は茶色、17匹は深紅色である。
ちがう色の2匹が遭遇したときその2匹は第3の色に変身するとして、
45匹すべてが同じ色になることはありえるだろうか。
<Sol> 灰色、茶色、深紅色のカメレオンの数をg,b,cとすると、
g - b,b - c,c - g の3による剰余は遭遇によって不変である。
元々のどの2種の頭数も法3で合同でないので、すべてが同じ色になることは
ありえない。 //
[類題]
●
○○
○○○
○○○○
・・・・・・
最初図のように碁石が無限に並んでる状態から始めて
左下と右下が白石であるような黒石を選んでそれら3つを
反対の色の碁石に置き換える
という操作を何回施しても、4段目までに黒石がなくならない
ということを示しなさい。(コンツェビチの問題)
(ヒント: Σ[k=1〜∞] f(k) のカタチの不変量をうまく構成する。)
<Sol> n段目にある黒石の数 bn を使って、
K = Σ[k=1〜∞] bk/2k-1
と定義する。
K は与えられた操作に対して不変で常に1である。(∵ 初期状態で1)
もしも4段目までに黒石がなくなったとすると、
K ≦ Σ[k=5〜∞] k/2k-1 = 3/4
となって K = 1 に反する。
したがって、4段目までに黒石が残らないようにするのは不可能である。 //
n-単体 xn=<a0,a1, ... ,an> の閉被覆 Σ={A0,A1, ... ,An} の各元 Ai が
ai の対辺 xn-1i=<a0, ... ,ai-1,ai+1, ... ,an> と交わっていないならば
A0∩A1∩ ... ∩An≠φ であることを示せ。
(ヒント: たとえば、ブローエル(Brouwer)の不動点定理を使う。)
<Sol> 対偶を示す。点集合 A と B の距離を d(A,B) で表すことにする。
A0∩A1∩ ... ∩An = φ とする。
p∈xn に対して μi(p) = d(p,Ai)/Σj=0n d(p,Aj)
とおくと、 0≦μi(p)≦1 (i = 0,1, ... ,n) かつ Σi=0n μi(p) = 1.
よって、 f(p) = μ0(p)a0 + μ1(p)a1 + ... + μn(p)an∈xn.
連続写像 f の不動点のひとつを q とする。
q は A0,A1, ... ,An
のいずれかに属するが、A0 に属するとして一般性を失わない。
∴ μ0(q) = 0.
∴ A0∩xn-10≠φ. //
ユークリッド空間 E ( = Rn )の合同変換群の有限部分群 G に対して
E は G に対する共通不動点(G のどの元に対しても不動な点)を持つことを示せ。
(ヒント: 合同変換 ⇒ 線形変換と平行移動の合成.)
行列式が1の3次直交行列 A に対して、 Ax = x ( x ≠ 0 )
となるタテベクトル x ∈ R3 が存在することを示せ。
位数 35 の群 G の 23 元集合 X への作用には必ず不動点があることを示せ。