組合せ論(Combinatorics)
序
メービウス関数
超平面による分割
ホイットニー数
参考書

[ 序 ]
組合せ論 とは、有限的な構造を 配置(configuration)、分布(distribution)
およびそれらの相関をもとにして研究する分野である。
以下、組合せ論のいくつかのトピックスについてまとめる。
[ メービウス関数 ]
数論的メービウス関数 μ:N → Z は
0 , n が square free でないとき
μ(n) = {
(-1)k , n が k 個の相異なる素数の積のとき
として定義され( μ(1) = (-1)0 =1 )、次のような顕著な性質を持っている。
定理 f, g:N → Z が f(n) = Σd|n g(d) (∀n∈N)
⇒ g(n) = Σd|n μ(n/d)f(d) (メービウスの反転公式)
G.C.Rota はメービウス関数に着目しそれを半順序集合上の関数に一般化することによって
数え上げ的組合せ論を一新させた。
例えば、「包除原理」(合併の元の数を共通部分の元の数で表す公式)や「差分法の基本定理」
(微積分の基本定理の離散版)と上記の 数論的反転公式 は 組合せ論的反転公式
として統一される。
集合 P 上の2項関係 ≦ は次の3条件を満たすとき 半順序とよばれる。
(P1) x ≦ x (反射律)
(P2) x ≦ y, y ≦ x ⇒ x = y (反対称律)
(P3) x ≦ y, y ≦ z ⇒ x ≦ z (推移律)
半順序 ≦ をもつ集合 P = (P, ≦) を 半順序集合(partially ordered set)
または ポセット(poset) という。
P の2元 x, y は x≦y か y≦x のいずれかなとき 比較可能(comparable)とよばれる。
どの2元も比較可能な半順序集合は 全順序集合(totally ordered set)とよばれる。
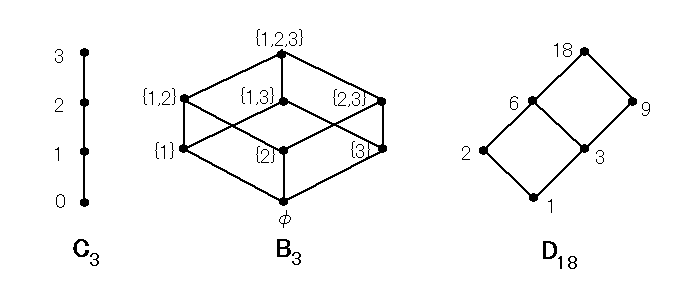
{0, 1, ... , n} に通常の大小による順序を入れたポセット Cn を (標準的)鎖(chain),
[n] = {1, 2, ... , n} のべき集合に包含関係 ⊂ による順序を入れたポセット Bn を
ブール束(Boolean lattice), 自然数 n のすべての約数の集合に整除関係による順序を
入れたポセット Dn を 約数ポセット(divisor poset), とよぶ。
ポセット P が 最小元 をもてばそれを 0P もしくは 0,
最大元 をもてばそれを 1P もしくは 1 で表すことにする。
P が最小元 0 をもつとき、P 上の メービウス関数 μ:P → Z は帰納的に
1 , x = 0 のとき
μ(x) = {
- Σy<x μ(y) , x > 0 のとき
で定義される。
クロネッカーのδを使うと、 Σy≦x μ(y) = δ(x, 0) とまとめられる。
例
1 , x = 0
1. Cn では μ(x) = { - 1 , x = 1
0 , x ≧ 2
2. Bn では μ(x) = (- 1)|x|
3. Dn では μ(x) は最初に述べた数論的関数
ポセット P と Q の 積(product) P×Q は成分ごとの順序で定義される。
定理 積ポセット P×Q のメービウス関数 μ は μ(x, y) = μP(x)μQ(y) である。
(∵) ν(x, y) = μP(x)μQ(y) が定義の帰納式をみたすことを示せば十分である。
Σ(u,v)≦(x,y) ν(u, v) = Σ(u,v)≦(x,y) μP(u)μQ(v)
= Σu≦x μP(u) Σv≦y μQ(v)
= δ(x, 0P)δ(y, 0Q)
= δ((x, y), (0P, 0Q)) //
ポセット P と Q が同型 P 〜 Q とは全単射 f:P → Q で f も f-1 も
順序を保つのが存在するときである。
定理 f:P → Q が同型写像 ⇒ μP(x) = μQ(f(x))
例
1. Bn は (C1)n とビット列の対応で同型で、
各ビットに対して μ(0) = 1, μ(1) = -1 ゆえ μ(x) = (-1)|x|.
2. 自然数 n の素因数分解が n = Πi pini のとき、Dn 〜 ×i Cni.
よって pini は ni = 1 か ni ≧ 2 で μ に対して -1 か 0 の寄与をする。
P の x≦y である2元 x, y に対して 区間 [x, y] = { z∈P| x≦z≦y } が定義される。
P の区間全体の集合を Int P で表示する。
有限ポセット P の メービウス関数 μ:Int P → Z は帰納的に
1 , x = y のとき
μ(x, y) = {
-Σx≦z<y μ(x, z) , x < y のとき
で定義する。これは、 Σx≦z≦y μ(x, z) = δ(x, y) とまとめられる。μ を μP ともかく。
P が最小元 0 をもつときは μ(x) = μ(0, x) であり、また区間 [x, y] はそれ自身で
最小元 x = 0[x, y] をもつポセットでこの上では新定義は旧定義に帰着される。
定理(メービウス反転公式) P をポセット,V をベクトル空間,f, g:P → V とする。
(MIT 1) すべての x∈P に対して f(x) = Σy≦x g(y) ⇒ g(x) = Σy≦x μ(y, x)f(y)
(MIT 2) すべての x∈P に対して f(x) = Σy≧x g(y) ⇒ g(x) = Σy≧x μ(x, y)f(y)
<証明> MIT 2 のみ示す。
Σy≧x μ(x, y)f(y) = Σy≧x (μ(x, y)Σz≧y g(z))
= Σz≧x (g(z) Σx≦y≦z μ(x, y))
= Σz∈P g(z)δ(x, z)
= g(x) //
MIT 1, MIT 2 の逆も成立する。
MIT 1 から数論的反転公式、差分法の基本定理が系として導ける。
<数論的反転公式の証明> f(m) = Σd|m g(d) (∀m∈N)とする。
Dn では f(m) = Σd≦m g(d) ということだから、[d, m] 〜 Dm/d と MIT より、
g(m) = Σd≦m μ[d,m](d, m)f(d) = Σd|m μDm/d(m/d)f(d) //
複素数値関数 f:N∪{0} → C に対して 微分の類似Δ が
Δf(n) = f(n) - f(n - 1)
積分の類似 S が
Sf(n) = Σi=0n f(i)
として定義される。( ただし f(-1) = 0 とする )
定理(差分法の基本定理) ΔSf(n) = f(n)
<差分法の基本定理の証明> Cn において g(m) = Sf(m) とおくと g(m) = Σi≦m f(i) だから、
[i, j] 〜 Cj-i と MIT より、
f(m) = Σi≦m μ(i, m)g(i) = g(m) - g(m - 1) = Δg(m) = ΔSf(m) //
MIT 2 から包除原理が系として導ける。
定理(包除原理(principle of inclusion and exclusion)) S が有限集合, S1, ... , Sn ⊂ S のとき、
| S - ∪i=1n Si | = |S| - Σ1≦i≦n |Si| + Σ1≦i<j≦n |Si∩Sj| - . . . + (-1)n |∩i=1n Si|
<包除原理の証明> x ∈ Bn に対して Sx = ∩i∈x Si とする。
f,g:Bn → N∪{0} を
f(x) = | Sx |
g(x) = | Sx - ∪i∈[n] - x Si |
と定義する。
定義から f(x) = Σy≧x g(y) だから、MIT 2 より、
| S - ∪i=1n Si | = g(φ)
= Σy≧φ μ(y)f(y)
= Σy∈Bn (-1)|y||∩i∈y Si| //
I(P) = { f| f:Int P → C } は通常の和およびスカラー乗法により C 上のベクトル空間
であるが、乗法を
(f*g)(x, y) = Σx≦z≦y f(x, z)g(z, y) (畳込み(convolution))
で定義することにより C 上の代数(algebra ,多元環)となる。
x≦y でないときには f(x, y) = 0 とすることで f ∈ I(P) の定義域を P×P に拡張すると
(f*g)(x, y) = Σz∈P f(x, z)g(z, y)
とかけることになる。
P の要素を整列させて x1, x2, ... , xn とする。( xi<xj ならば i<j )
行と列が x1, x2, ... , xn で添え字づけられた複素行列の集合 Mat(P) を
M ∈ Mat(P) ⇔ mx,y = 0 ( x≦y でないとき )
により定義する。
定理 I(P) 〜 Mat(P) , f ├→ Mf = ( f(x, y) )
例 B2 を φ,1 ,2 ,1 2 と整列させると
┌ 1 -1 -1 1 ┐
| 0 1 0 -1 |
| 0 0 1 -1 | = Mμ
└ 0 0 0 1 ┘
系
(1) I(P) は 1(x,y)=δ(x,y) で与えられる単位元 1:Int(P) → C をもつ。
(2) f ∈ I(P) が可逆 ⇔ ∀x∈P, f(x, x) ≠ 0
ζ ∈ I(P) を
ζ(x, y) = 1 ∀[x, y] ∈ I(P)
で定義する。
系 μ = ζ-1
(∵) (μ*ζ)(x, y) = Σx≦z≦y μ(x, z)ζ(z, y)
= Σx≦z≦y μ(x, z)
= 1(x, y) //
ポセット L のどんな2元 x ,y も下限 x∧y および上限 x∨y を持つとき L は 束(lattice)
とよばれる。( x∧y は「 x ミート y 」,x∨y は「 x ジョイン y 」 と読む )
例
束 x∧y x∨y
------------------------------------------
Cn min{x, y} max{x, y}
Bn x ∩ y x ∪ y
Dn gcd(x, y) lcm(x, y)
形式的1次結合のなす複素ベクトル空間
M(L) = { Σx∈L cxx | cx ∈ C }
を考える。 L の要素 x に対して
εx = Σz≦x μ(z, x)z
と定義する。
補題
(1) L の要素 x に対して x = Σz≦x εz.
(2) 集合 B = { εx| x ∈ L } は M(L) の基底である。
(∵) (1) MIT 1 の逆を εx の定義に適用すれば immediate.
(2) |B| = |L| なので B が生成系であることを示すだけでOKでこれは (1) からいえる。 //
乗法を
εx・εy = δ(x, y)εx
で定義すると M(L) は代数となり メービウス代数 とよばれる。
定理 x, y ∈ L について、 xy = x∧y .
(∵) xy = (Σz≦x εz)(Σw≦y εw)
= Σz≦x , w≦y εzεw
= Σz≦x , w≦y δ(z, w)εz
= Σz≦x , y εz
= Σz≦x∧y εz
= x∧y //
定理(Weisnerの定理) L が有限束,c ∈ L - {1} ⇒ Σx∧c = 0 μ(x, 1) = 0
<証明> cε1 = Σd≦c εdε1 = 0 (∵ d≦c<1 ゆえ d≠1 だから εdε1 = 0 )
∴ 0 = cε1 = c Σx≦1 μ(x, 1)x = Σx≦1 μ(x, 1)(x∧c)
0 の係数を比べると与式を得る。 //
定理(Weisnerの定理の双対) L が有限束,d ∈ L - {0} ⇒ Σx∨c = 1 μ(0, x) = 0
ポセット P の要素 x, y について、x<y であるが x<z<y である z は存在しないとき y は x を
カバーする もしくは y は x の 直後の元 もしくは x は y の 直前の元 とよび、
ここでは y↓x で表示することにする。
0 をカバーする要素を アトム(atom),1 にカバーされる要素を 余アトム(coatom)という。
P のアトムの全体および余アトムの全体の集合をそれぞれ A(P), A*(P) もしくは A, A*
で表示する。
例
P A(P) A*(P)
-------------------------------------------------
Cn {1} {n - 1}
Bn { x | |x| = 1 } { x | |x| = n-1 }
Dn {素数 p| p|n} {n/p| p は素因数}
系(P.Hall) 有限束 L に対して次が成り立つ。
(1) ∨A(L)≠1 ⇒ μ(0, 1) = 0
(2) ∧A*(L)≠0 ⇒ μ(0, 1) = 0
ポセット P の全順序部分集合 C を 鎖(chain)とよぶ。有限な鎖 C の 長さ l(C) は
|C| - 1 で定義する。有限な鎖 C = { x0, x1, ... , xl } ( x0 < x1 < . . . < xl ) を
C:x0 < x1 < . . . < xl とも表す。C 〜 Cl である。
0 および 1≠0 をもつポセット P の 順序複体(order complex)ΔP を
Δ(P) = { 鎖 C | 0 < x0 ,xl < 1}
で定義する。鎖の部分集合も鎖なので Δ(P) は(抽象的な)単体複体である。
次元 l の単体の集合 { C∈Δ(P)| l(C) = l } を Δl(P) で表示する。
Δ-1(P) = {φ} ,Δl(P) = φ ( l≦-2 )とする。
補題 l≧0 ⇒ (ζ- 1)l(0, 1) = |Δl-2P|
(∵) 1 , x < y
(ζ- 1)(x, y) = {
0 , x = y
∴ (ζ- 1)l(0, 1) = Σ0≦x0≦ ... ≦xl-2≦1 (ζ- 1)(0, x0)...(ζ- 1)(xl-2, 1)
= Σ0<x0< ... <xl-2<1 1
= |Δl-2P| //
定理 μ(0, 1) = Σl≧-1 (-1)l|Δl(P)|
<証明> 補題 と (ζ- 1)k+1(0, 1) = 0 ( k は 0 と 1 を結ぶ最長の鎖の長さ)
により
μ(0, 1) = ζ-1(0, 1)
= [1 + (ζ- 1)]-1(0, 1)
= Σl≧0 (-1)l(ζ- 1)l(0, 1)
= Σl≧0 (-1)l|Δl-2(P)|
= Σl≧-1 (-1)l|Δl(P)| //
[ 超平面による分割 ]
[ ホイットニー数 ]
どんな要素もいくつかのアトムのジョインとなっている束を アトミック(atomic ,原子的)とよぶ。
0 をもつポセット P の要素 x の 高さ(height)h(x) は
h(x) = sup { l(C)| C は 0 と x を結ぶ鎖 }
で定義する。
有限ポセット P に対してどんな2要素 a ,b を結ぶ極大な鎖も同じ長さであるという条件を JD 条件
とよぶ。(JD は Jordan-Dedekind の略) JD 条件をみたしている束を JD 束(JD-lattice)という。
JD 束 L は高さ関数 h が
h(x) + h(y) ≧ h(x∧y) + h(x∨y) (∀x, y ∈ L )
をみたしているとき セミモジュラー(semimodular)とよばれる。
アトミックかつセミモジュラーな束は 幾何束(geometric lattice)という。(幾何束は
束論の創始者バーコフ(Birkhoff)によるもので、ホィットニーによる「マトロイド」と対応する概念である。)
定理( Basterfield and Kelly 1968, Greene 1970, Heron 1973 )
有限幾何束 L においては、 |A(L)| ≦ |A*(L)|
Dowling と Wilson はこれを次のように一般化した。
DW 定理 有限幾何束 L においてホイットニー数の間には
W1 + W2 + . . . + Wk ≦ Wr-k + . . . + Wr-2 + Wr-1 ( r = ρ(L) ,1 ≦ k ≦ r - 1 )
なる大小関係が成り立つ。
《 参考書 》
[1] 日比 孝之 , 数え上げ数学 , 朝倉書店 , 1997
[2] 日比 孝之 , 可換代数と組合せ論 , シュプリンガー東京 , 1995
[3] Welsh , Matroid Theory , Academic Press , 1976
← 数学ノートに戻る