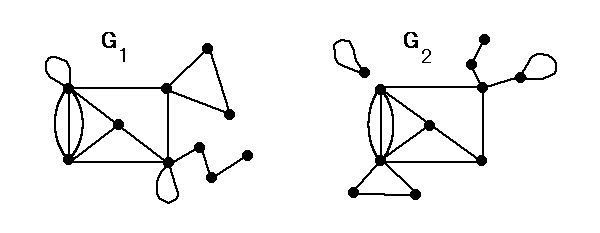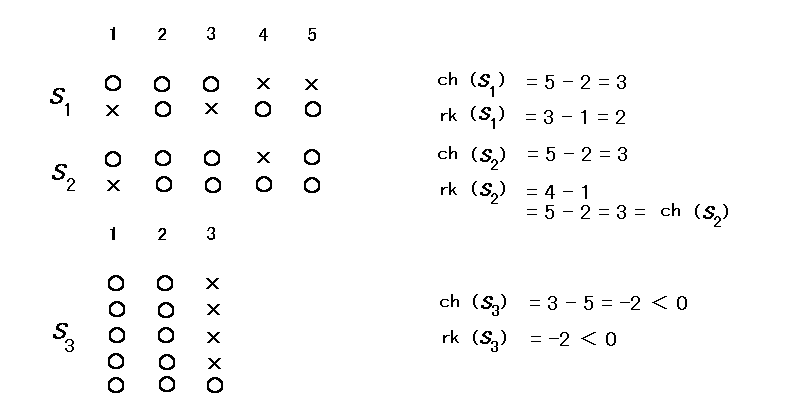マッチングと同様の概念として独立点集合というのがある。
G の点の集合 S はどの異なる2要素も非隣接なとき G の 独立点集合 もしくは単に 独立集合 とよばれる。(空集合も独立集合.)
G の頂点たちを α1 ~ αk の k 色で塗り分けて隣接するどの2点も異なる色となるとき、この着色を k 染色 という。つまり G の k 染色とは頂点集合 V(G) を k 個の独立集合に分割することに他ならない。
k 染色が存在する最小の k を G の 染色数(chromatic number)といい χ(G) で表す。
χ(G) = k であるグラフ G を k 染色的、χ(G) ≦ k であるグラフ G を k 染色可 という。
[ 定理 11.1 ] グラフ G について次は同値である。
(1) 4 染色可.
(2) E(G) は2つのカットの合併.
<証明> (1)⇒(2); G は色 α,β,γ,δ でたかだか 4 染色されているとする。
G はループをもたない。
両端点の色が αβ か βγ か γδ の辺全体を A1 ,
βδ か δα か αγ の辺全体を A2 とする。
誘導部分グラフ G[A1] ,G[A2] は2部グラフであり、A1 を含むカット ω1 ,A2 を含むカット ω2 が存在する。
E(G) = ω1 ∪ ω2 である。
(2)⇒(1); E(G) が2つのカット ω1 ,ω2 の合併とする。
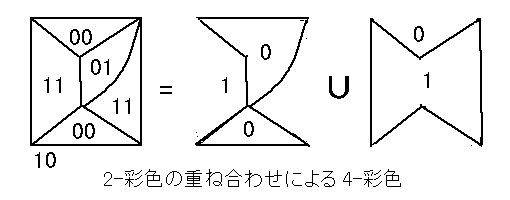
部分グラフ G[ω1] ,G[ω2] は2部グラフで G[ω1] も G[ω2] も色 0 ,1 でたかだか 2 染色できる。
G の頂点の (0,0) ,(0,1) ,(1,0) ,(1,1) によるたかだか 4 着色をこれら 2 染色の重ね合わせで定めるとたかだか 4 染色となっている。 //
平面グラフの面の k 彩色 が k 染色の双対として定義される。
[ 系 ] 平面グラフ G について次は同値である。
(1) 4 彩色可.
(2) E(G) は2つのサイクルの合併.
次の定理は有名である。
しかしながら、現在までに知られてる証明はコンピューターによるチェックが必要なもので、満足行く証明とは言えない。
[ 定理 11.2 ] どんなブリッジをもたない平面グラフも 4 彩色できる。(4色定理)
[ 系 ] どんなブリッジをもたない平面グラフの辺集合も2つのサイクルで cover できる。
「4色定理をエレガントに証明せよ」という問題を 4色問題 とよべば、4色問題は100年以上に渡って未解決の珠玉の難問ということになる。
しかしながら、4 を 5 とした5色定理の証明はむずかしくない。
[ 定理 11.3 ] どんなブリッジをもたない平面グラフも 5 彩色できる。( 5色定理 Heawood 1890 )
<証明> ブリッジをもたない平面グラフの双対グラフはループをもたないので、ループをもたない平面グラフ G が 5 染色可能なことを示せばよい。
|V(G)| についてのインダクションで示す。
G には次数が高々 5 の頂点が存在する。(10章の演習問題の2)
そのうちのひとつを v とする。
deg(v)≦4 のとき; G - v を帰納法の仮定で5色以下で染色して、vには隣接する頂点と異なる色を割り振ればよい。
deg(v) = 5 のとき; v に隣接する2点 x , y でお互いに非隣接なのが存在する。(∵ そうでないとすると、完全グラフ K5 が生じてしまうから)
辺 vx と辺 vy を縮約したグラフを G' とする。
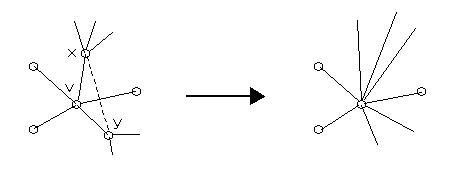
G' もループはもたないので、帰納法の仮定から5色で十分で、この染色を G に引き戻して v の色を隣接する頂点とは異なった色にすれば G の5色以下での染色がえられる。 //
[ 定理 11.4 ] 次は同値である。
(1) 4色定理.
(2) どんなブリッジをもたない 3 正則平面グラフも 4 彩色できる.
<証明> (1)⇒(2); あきらか。
(2)⇒(1): 面の縮約( = 頂点の除去の双対 )の逆の頂点の「膨らまし」を何回か施すことによりブリッジをもたない平面グラフ G はブリッジをもたない 3 正則平面グラフ G~ になる。
G~ が 4 彩色可能であれば、逆の変形によりその 4 彩色は G の 4 彩色となる。
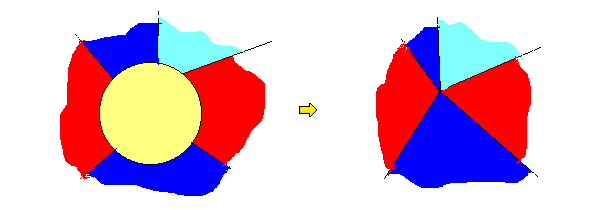
//
[ 定理 11.5 ] 3 正則グラフ G について次は同値である。
(1) G は2つのサイクルの合併.
(2) G は隣接する辺が異なる色になるような辺の3色分けが可能.
<証明> (2)⇒(1); 3色を 1, 2, 3 とする。
色 1 と色 3 の辺全体を z1 色 2 と色 3 の辺全体を z2 とすると z1 も z2 もサイクルで G の辺集合を cover している。
(1)⇒(2); E(G) = z1 ∪ z2 ( zi はサイクル ) とする。
z1 - z2 の辺を色 1
z2 - z1 の辺を色 2
z1 ∩ z2 の辺を色 3
で着色すれば所望の辺の3色分けとなる。 //
(2)のような辺の色分けを テイト色分け(Tait coloring)という。
4色問題を攻略するのに次の命題を出発点とする人が多い。
[ 系 ] 次は同値。
(1) 4色定理.
(2) どんなブリッジをもたない 3 正則平面グラフも Tait 色分けが可能.
3色 α,β,γ でテイト色分けされた 3 正則グラフにおいてαかβで着色された辺全体は各連結成分が長さ even のサーキットであるようなサイクルで、αとβで決まる テイトサイクル とよぶ。
[ 定理 11.6 ] 3 正則グラフ G が3色 α,β,γ によりテイト色分けされているとき、どのカット K においても α の辺の数 nα, β の辺の数 nβ, γ の辺の数 nγ とすると
nα ≡ nβ ≡ nγ ≡ 0 (mod 2)
となっている。(パリティー補題)( Isaacs )
<証明> テイトサイクルと K は even で交わるから。 //
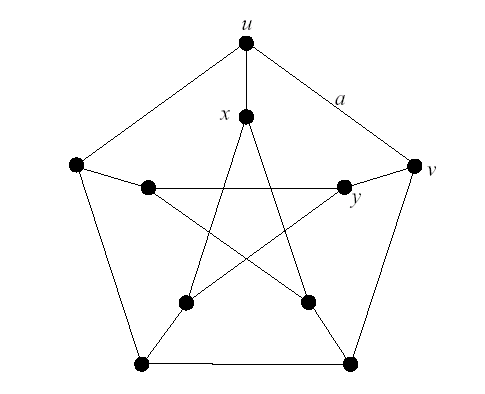
[ 系 ] ペテルセングラフは2つのサイクルで cover できない。
<証明> α,β,γ でテイト色分けできたとして矛盾をみちびけばよい。
図のカット K にパリティー補題を適用すると図の2つのケースを考えればよいことになる。
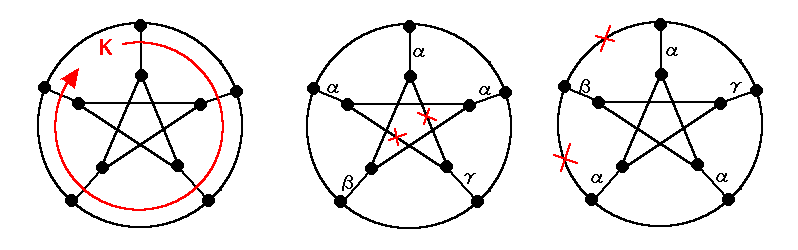
どちらのケースも×印の辺の色を考えると矛盾する。 //
<別証> ( By Naserasr and Skrekovski )
a, b, c でテイト色分けできたとして矛盾をみちびけばよい。
外側のサーキットは長さが5の奇数なのでa, b, c のどれもが使われる。
図で x に接合する内側のサーキットの2辺のうちどちらかは a が使われる。
同様にして y に接合する内側のサーキットの2辺のうちどちらかでも a が使われる。
つまり内側のサーキットで a は2回以上使われることになる。b, c についても同様。
これは内側のサーキットの長さが5であることと矛盾する。
//
テイト色分け不可能なブリッジをもたない 3 正則グラフは スナーク(snark)とよばれている。
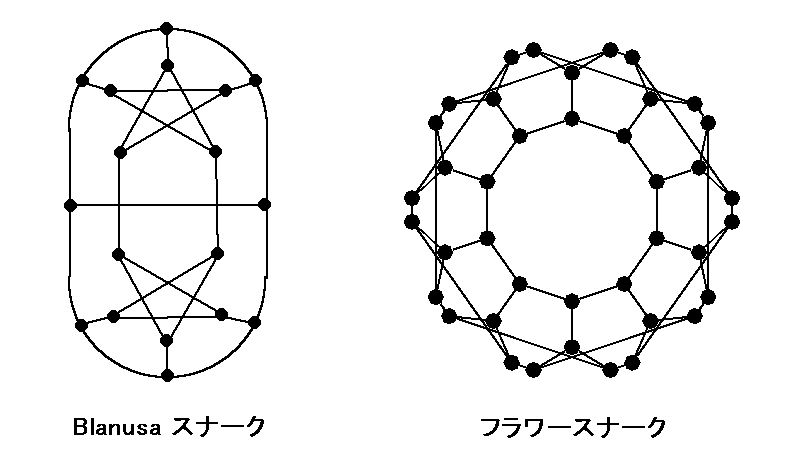
スナークについての次の予想が示せれば4色定理も示せたことになる。
スナーク予想 どんなスナークもペテルセングラフをマイナーとしてもつ。
[ 定理 11.7 ] 任意のグラフ G について次は同値である。
(1) E(G) は2つのサイクルの合併.
(2) G にはサイクライザーであるサイクル ζ が存在する.
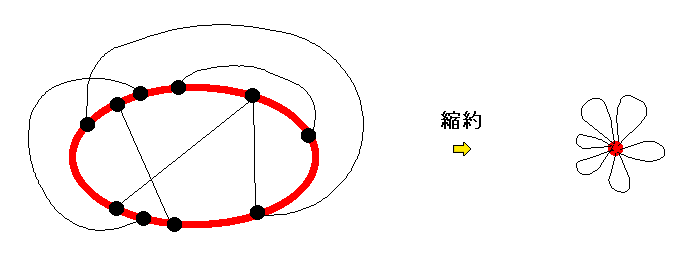
[ 系 ] ハミルトンサーキットをもつグラフの辺集合は2つのサイクルで覆える。
(∵) ハミルトンサーキットを縮約すると1点にループがついた偶グラフになるから。
//
[ 定理 11.8 ] 任意の単純グラフ G について次は同値である。
(1) E(G) は2つのサイクルの合併.
(2) G にはサイクライザーである正則な極大サイクル ζ が存在する.
定理 11.2 の系に関連して次の Jaeger の定理がある。12章で知られている証明を少しアレンジして紹介するが若干メンドウである。
[ 定理 11.9 ] どんなブリッジをもたないグラフの辺集合も3つのサイクルで cover できる。( Jaeger 1975 )
被覆についての次の予想は有名である。(「高々」のところは「丁度」と読み替えても良い.)
2重被覆予想 ブリッジをもたないどんなグラフの辺集合もいくつかのサイクルで高々2重に cover できる。( Seymour 他 )
ついでなので色分けの有名な結果を簡単に補っておく。用語は逐一ていねいに説明しないが常識的に判断できる範囲で記述する。
有向グラフ D の各有向辺 e に φ(e) という加法群( 演算が加法とよばれ記号 + で表示されるアーベル群(可換群)) A の元を対応させて、これを e の始点から終点へ行くときの仕事量とする。
逆向きに行くときは - φ(e)の仕事量を必要とすると考える。
このとき、
[ 補題 ] このシステムの「ポテンシャル」、すなわち 関数 p:V(D) → A で
e = (x,y) なら φ(e) = p(y) - p(x) となるのが存在する
⇔ 任意のサーキットを一周する時の仕事量(の和)が 0.
(∵) ⇒; ポテンシャル p が存在するなら、任意の歩道(walk)上の仕事量はその端点のポテンシャルの差である。とくにどんな閉歩道上でも仕事量は 0、よってサーキット上でも 0 である。
逆; D は連結としてよい。任意のサーキット上の仕事量が 0 とする。
閉歩道 W がサーキットであれば仕事量は 0.
W が頂点 x で重複していれば、x は W をそれより短い閉歩道 W1,W2 に分割するから、帰納的に W 上の仕事量も 0 となる。
P1,P2 が2つの (x,y)-歩道のとき、P1 に沿って x から y に行き P2 を逆にたどって戻ってくればそれは閉歩道で仕事量は 0 なので、P1 上の仕事量と P2 上の仕事量は等しいことになる。
よって、頂点 x0 を固定すると、p(x) を x0 から x まで行くのに必要な仕事量として定義できることになる。この関数 p はポテンシャルとなる。
(∵ 辺 e = (x,y) とする。(x0,x)-歩道 Px ,(x0,y)-歩道 Py をとる。Px∪e∪Py は閉歩道で、仕事量は 0.
∴ p(x) + φ(e) + (- p(y)) = 0 ∴ φ(e) = p(y) - p(x).) //
[ 定理 11.10 ] 平面三角化グラフ G に対して次は同値である。( Heawood )
(1) 3 染色可.
(2) 偶グラフである.
<証明> (1)⇒(2); 対偶を考えれば easy.
(2)⇒(1); 各頂点は偶点とする。双対 G* は2部グラフなので G の面を赤と青の2色で彩色できる。
赤の面を右にする各辺の向き付けを考える。
C を G のサーキットとする。C の辺のうち、それに接する赤の面を C の内側にもつのがα本、外側にもつのがβ本 あるとする。
また、C の内側には sコの赤の面とtコの青の面があるとする。
C 上か C の内側にある辺の総数は 3s + β であり、また 3t + α でもある。
よって、C を反時計回りに回るときの仕事量は、φ(e) = 1 ∈ Z (∀e) として、
β - α = 3s - 3t ≡ 0 (mod 3) である。
よって、補題より、V(G)上の関数 p(x)∈Z で、各辺 (x, y) に対して p(y) - p(x) ≡ 1 となるのがある。
p(x) は 0 か 1 か 2 としてよい。この p は G の 3 染色である。 //
[ 定理 11.11 ] ブリッジをもたない 3 正則平面グラフ G について次は同値である。( Heawood )
(1) G は 4 彩色可.
(2) G の {-1, 1} による 2 点着色で、各面に接合する頂点の数字の和が 3 の倍数になるのがある.
<証明> (1)⇒(2); 4 彩色可とすると、E(G) は2つのサイクル z1,z2の合併で、辺はテイト色分けできる。
各頂点に対し、接合する辺の色 1、2、3 が時計回りのとき 1 、反時計回りのとき -1 を割り当てれば良い。(確かめよ.)
(2)⇒(1); 条件(2)のように 2 点着色ができたとする。
G の線グラフ L(G) も平面グラフで、2種類の面を持つ。ひとつは、各 x∈V(G) に対応し、x を内部にもつ三角面 Fx,もうひとつは、G の各面 F に対応して F と同じ辺数をもち F に含まれる面 F ’である。
Fx の辺を時計回りに向き付ける L(G) の向き付けを考える。
また、L(G) の辺 e に対し、e の2端点に対応する G の2辺に接合する G の頂点に割り当てられた数を e の重みとよび w(e) で表す。
L(G) の辺をたどるときの仕事量を、e を向き付けの向きにたどるとき w(e),逆にたどるとき - w(e) として定める。以下、和や差は mod 3 で考える。
L(G) の各面の周囲をたどるときの仕事量は 0 となる。
L(G) のかってなサーキット C に対し、C を時計回りに回るときの仕事量は、C 内のすべての面についてそのまわりを時計回りにたどったときの仕事量 0 の和で、0 となる。(∵ C の内部の辺では相殺される.)
反時計回りでも同様に 0 となる。
補題より、V(L(G)) の各頂点 x にポテンシャル p(x) を割り当てできる。
p(x) は 0,1,2 いずれかの値にできる。
p(x) は L(G) の 3 染色となる。
(1)⇒(2)で述べたことの逆で G の 4 彩色が得られる。 //
[ 定理 11.12 ] 次数 3 の頂点を含まない平面グラフは 3 彩色可。( Grötzsch 1959 )
[ 演習問題 ] ( → 解答 )
1. ループをもたないグラフ G に対して不等式 χ(G) ≦ (1/2)(1 + √(1 + 8ε)) が成り立つことを証明せよ。
2. グラフ G のどの2つの奇サーキットも頂点を共有するとき χ(G) ≦ 5 であることを示せ。( 長さが奇数のサーキットを奇サーキットという.)
3. グラフ G について次は同値であることを証明せよ。
(1) 2部グラフである.
(2) どの部分グラフ H に対しても H の頂点の半分以上が独立.
4. Blanusa スナーク、フラワースナークがたしかにスナークであることを確めよ。
5. χ(G) = r ならば G は Kr をマイナーとしてもつ、という予想(Hadwiger 予想)がある。この予想が r = 1, 2, 3, 4 のとき成り立つことを示せ。
ここでは11章で紹介した次の定理(定理 11.9)の証明を目標にしてマトロイド理論について述べることにする。
[ Jaeger の定理 ] どんなブリッジをもたないグラフの辺集合も3つのサイクルで cover できる。
グラフの辺の集合が非輪状という性質はベクトル空間の部分集合に対する1次独立という性質と良く似ている。
このことに着目して、特に双対性の定式化の為に、Whitney はマトロイドという概念を考案した。( van der Waerden の代数的独立性についての公理的考察などにもマトロイド概念の萌芽が見られる.)
位相空間の同値な定義がいろいろあるのと同様、マトロイドにも種々の定義の仕方がある。
有限集合 E 上の マトロイド(matroid)M = M(E) とは E と E の部分集合の集合 I で次を満たすののペア (E, I) をいう。(独立集合公理)
(I1) φ ∈ I.
(I2) X ∈ I, Y ⊂ X ⇒ Y ∈ I.
(I3) X, Y ∈ I, |X| = |Y| + 1 ⇒ ∃x ∈ X - Y, Y ∪ x ∈ I.
I の要素を 独立集合 ,E の部分集合で独立でないのを 従属集合 とよぶ。E は M の 台 または 台集合 とよぶことにする。
例 E をベクトル空間 V の有限部分集合,I を E の1次独立な部分集合の全体とすると、(E, I) はマトロイドで ベクトルマトロイド とよばれる。
また、グラフ G に対して森全体の集合を I としたとき、(E(G), I) もマトロイドで G の サーキットマトロイド とよばれる。
<(E(G), I) がマトロイドである理由> (I1),(I2)はあきらか。
(I3); X , Y を森で |X| = |Y| + 1 とする。
どの x ∈ X - Y についても Y ∪ x が森でないとすると x は <Y> の同じ連結成分の2頂点をむすんでいることになり X ∪ Y のコサーキットランクは |Y| となる。
しかしながら X ∪ Y は森 X を含むのでコサーキットランクは |X| = |Y| + 1 以上ゆえこのようなことはありえない。 //
マトロイド M = M(E) に対して極大独立集合を ベース( base ,基 ,基底 ),極小従属集合を サーキット( 閉路 )とよぶ。
ランク関数 ρ: P(E) → Z を ρ(A) = max{ |X| | I ∋ X ⊂ A } で定義し ρ(A) を A の ランク とよぶ。とくに ρ(E) を M の ランク という。 グラフのサーキットマトロイドにおけるランクは r で表すことにする。
E の部分集合 A はかってな x ∈ E - A について ρ(A ∪ x) = ρ(A) + 1 であるとき M の フラット(flat)もしくは 閉集合 とよぶ。
x ∈ E, A ⊂ E について ρ(A ∪ x) = ρ(A) のとき x は A に 従属している とよび x ~ A で表示する。
σ(A) = { x ∈ A | x ~ A } を A の 閉包(closure)とよび関数 σ: P(E) → P(E) を M の 閉包関数 とよぶ。σ(A) を A- ともかく。
マトロイドはベース,サーキット,ランク関数,閉包のいずれを使っても定義できる。
[ 定理 12.1 ] E の部分集合の空でない集合 B が E 上のマトロイドのベース全体の集合であるための必要十分条件は B が次をみたすことである(ベース公理):
(B1) B の要素に B の要素が真に含まれることはない.
(B2) B1, B2 ∈ B, x ∈ B1 ⇒ ∃y ∈ B2, (B1 - x) ∪ y ∈ B .(ベース交換性質)
[ 定理 12.2 ] E の空でない部分集合の集合 C が E 上のマトロイドのサーキット全体の集合であるための必要十分条件は C が次をみたすことである(サーキット公理):
(C1) C の要素に C の要素が真に含まれることはない.
(C2) C1, C2 ∈ C, C1 ≠ C2,x ∈ C1 ∩ C2 ⇒ ∃C3 ∈ C, C3 ⊂ (C1 ∪ C2) - x .(サーキット交換性質)
[ 定理 12.3 ] 関数 ρ: P(E) → Z が E 上のマトロイドのランク関数であるための必要十分条件は ρ が次をみたすことである(ランク公理):
(R1) 0 ≦ ρ(A) ≦ |A| .
(R2) A ⊂ B ⊂ E ⇒ ρ(A) ≦ ρ(B) .
(R3) ρ(A ∪ B) + ρ(A ∩ B) ≦ ρ(A) + ρ(B) .
[ 定理 12.4 ] 関数 ρ: P(E) → Z が E 上のマトロイドのランク関数であるための必要十分条件は ρ が次をみたすことである(ランク公理):
(R'1) ρ(φ) = 0 .
(R'2) ρ(X) ≦ ρ(X ∪ y) ≦ ρ(X) + 1 .
(R'3) ρ(X ∪ y) = ρ(X ∪ z) = ρ(X) ⇒ ρ(X ∪ y ∪ z) = ρ(X) .
[ 定理 12.5 ] 関数 σ: P(E) → P(E) が E 上のマトロイドの閉包関数であるための必要十分条件は σ が次をみたすことである(閉包公理 ( by Rota )):
(S1) X ⊂ σ(X) .
(S2) X ⊂ Y ⇒ σ(X) ⊂ σ(Y) .
(S3) σ(X) = σσ(X) .
(S4) y ∈ E - σ(X),y ∈ σ(X ∪ {x}) ⇒ x ∈ σ(X ∪ {y}) .
グラフ G のサーキットマトロイド M(G) = M(E(G)) では
ベースは極大森
サーキットは通常のサーキット
ランクはコサーキットランク
フラットはコサイクロイドの補集合
となっている。
以後マトロイド M といったら 集合 E と I, B, C, ρ,σのいずれかとのペアを指す。
2つのマトロイド M(E1),M(E2) に対して全単射 Φ: E1 → E2 で独立性やランクやサーキットであることなどを保つのが存在するとき 同型(isomorphic)とよび M(G1) ~ M(G2) で表示する。
例 図のグラフ G1, G2 に対して M(G1) ~ M(G2).
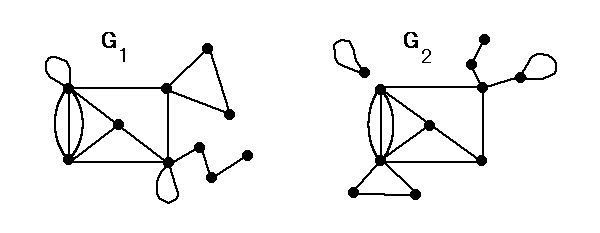
また、図のグラフ G3, G4 に対しても M(G3) ~ M(G4).
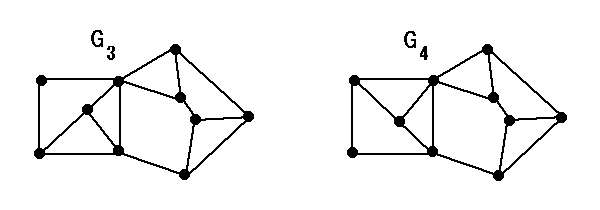
マトロイド M はあるグラフ G があって M ~ M(G) となるとき グラフ的(graphic)とよばれる。
グラフ G のボンドをサーキットとしても E(G) 上のマトロイドとなり G の ボンドマトロイド もしくは コサーキットマトロイド とよび M*(G) で表示する。
マトロイド M はあるグラフ G があって M ~ M*(G) となるとき 余グラフ的(cographic)とよばれる。
集合 E 上の集合空間 ∑ に対して空集合を除いて極小な ∑ の要素をサーキットとすることで E 上のマトロイド M(∑) がえられる。
マトロイド M はある集合空間 ∑ があって M ~ M(∑) となるとき バイナリー(binary,2値的)とよぶ。
M が 集合 E 上のマトロイド,A ⊂ E のとき、A に含まれる M のサーキットをサーキットとしてえられる A 上のマトロイドを M の A への 制限(restriction)といい M × A または M | A で表す。
Min{ C ∩ A | C は M のサーキット } をサーキットの族としてえられる A 上のマトロイドを M の A への 縮約(contraction)といい M ・ A で表す。
M から制限と縮約を繰り返してえられるマトロイドを M の マイナー(minor)とよぶ。
どのサーキットのサイズも偶数であるようなマトロイドを 2部マトロイド ,E がいくつかのサーキットの素和であるようなマトロイドを 偶マトロイド とよぶ。
[ 命題 12.1 ] マトロイド M において次が成り立つ。
(1) ベース B1, B2 に対して |B1| = |B2|.
(2) ρ(A ∪ B) + ρ(A ∩ B) ≦ ρ(A) + ρ(B).
<証明> (1) ベース交換性質を繰り返して示される。
(2) X を A ∩ B のベース( = 極大独立集合 )とする。X を A のベース Y に拡張し Y を A ∪ B のベース Z に拡張する。
X ∪ (Z - Y) は B で独立なので
ρ(B) ≧ ρ(X ∪ (Z - Y))
= |X ∪ (Z - Y)|
= |X| + |Z| - |Y|
= ρ(A ∩ B) + ρ(A ∪ B) - ρ(A). //
さて、双対性を定式化して調べることにしよう。
M = (E, ρ) に対して ρ*: P(E) → Z を A ⊂ E に対して
ρ*(A) = |A| + ρ(E - A) - ρ(E)
と定める。
[ 定理 12.6 ] M* = (E, ρ*) は E 上のランク公理を満たすマトロイドである。
<証明> (R1)と(R3)のみ示す。
(R1) ρ(E - A) ≦ ρ(E) から ρ*(A) ≦ |A| は immediate.
B = E - A として(R3)より ρ(E) + ρ(φ) ≦ ρ(A) + ρ(E - A).
∴ ρ(E) - ρ(E - A) ≦ ρ(A) ≦ |A|. ∴ ρ*(A) ≧ 0.
(R3)は次のように示される:
ρ*(A ∪ B) + ρ*(A ∩ B)
= |A ∪ B| + |A ∩ B| + ρ(E - (A ∪ B)) + ρ(E - (A ∩ B)) - 2ρ(E)
= |A| + |B| + ρ((E - A) ∩ (E - B)) + ρ((E - A) ∪ (E - B)) - 2ρ(E)
≦ |A| + |B| + ρ(E - A) + ρ(E - B) - 2ρ(E) ( by (R3))
= ρ*(A) + ρ*(B). //
ρ* の定義は若干複雑だが、M と M* の関係は実は単純である。
[ 定理 12.7 ] M* のベース全体と M のベースの補集合全体は一致する。
<証明> B* を M* のベースとする。E - B* が M のベースであることを示す。逆は同様に示される。
独立性から |B*| = ρ*(B*).∴ ρ(E - B*) = ρ(E).
よって E - B* が M で独立なことを示せばよい。
|B*| + ρ(E - B*) - ρ(E) = |E| + ρ(E - E) - ρ(E) より ρ(E - B*) = |E - B*|.
以上から E - B* は M で独立である。 //
[ 系 ] M** = M .(双対性)
[ 定理 12.8 ] グラフ G に対して M*(G) = (M(G))*.
<証明> C* が (M(G))* のサーキットであることと C* が G のコサーキットであることが同値なことをいえば良い。
C* を G のコサーキットとする。
C* が (M(G))* で独立とすると C* は (M(G))* のベース B* に拡張でき C* ∩ (E - B*) = φ.
E - B* が G の極大森であることからこのようなことは起こりえない。
よって C* は (M(G))* で従属で (M(G))* のサーキットを含むことになる。
逆に D* が (M(G))* のサーキットとすると D* は (M(G))* のどのベースにも含まれないから M(G) のかってなベース、つまり G のかってな極大森と交わる。
よって D* は G のコサーキットを含む。
以上から C* が (M(G))* のサーキットであることと C* が G のコサーキットであることは同値である。 //
マトロイド M の台の部分集合は M* のサーキットであるとき M の コサーキット(余閉路,余サーキット)という。
上記の定理より グラフ G のサーキットマトロイドのコサーキットは G のコサーキットと一致する。
同様にして M の 余ベース(cobase),余ランク(corank),余独立集合(co-independent set)が定義できる。
[ 命題 12.2 ] マトロイドのどのコサーキットとベースも交わる。
<証明> C* は E 上のマトロイド M のコサーキット,B は M のベースとする。
C* ∩ B = φ とすると C* ⊂ E - B.
すると M* のサーキット C* が M* のベースに含まれていることになり不合理。 //
[ 系 ] マトロイドのどのサーキットと余ベースも交わる。
(∵) 命題を M* に適用すれば示される。 //
[ 定理 12.9 ] G* がグラフ G の抽象的双対 ⇒ M(G*) ~ (M(G))*.
<証明> G* がグラフ G の抽象的双対であることから G の辺集合から G* の辺集合への全単射があり G のサーキットと G* のコサーキットが対応する。
よって M(G) のサーキットが M(G*) のコサーキットに対応し M(G) ~ (M(G*))*.
∴ (M(G))* ~ (M(G*))** = M(G*). //
[ 系 ] G* が連結平面グラフ G の双対グラフ ⇒ M(G*) ~ (M(G))*.
M1, M2, . . . , Mk が台として E をもつマトロイドのとき
{ X1 ∪ X2 ∪ . . . ∪ Xk | Xi は Mi の独立集合 } を独立集合族とすることにより E 上のマトロイドがえられる。これを M1, M2, . . . , Mk の 合併(union)とよび M1 ∪ M2 ∪ . . . ∪ Mk で表示する。
[ 定理 12.10 ] Mi のランク関数を ρi とすると M1 ∪ M2 ∪ . . . ∪ Mk のランク関数 ρ は
ρ(X) = min {ρ1(A) + ρ2(A) + . . . + ρk(A) + |X - A| | A ⊂ X }
となる。( Edmonds-Fulkerson 1965 )
[ 系 ] マトロイド M = (M, ρ) について次は同値。
(1) k 個の互いに素なベースをもつ.
(2) ∀A ⊂ E ,kρ(A) + |E - A| ≧ kρ(E).
(∵) k 個の互いに素なベースをもつことは M の k 個のコピーの合併のランクが kρ(E) 以上であることと同値ゆえ。 //
[ 系の系 ] グラフ G について次は同値。
(1) k 個の互いに素な極大森をもつ.
(2) ∀H ⊂ G ,k(dim Z*(G) - dim Z*(H)) ≦ |E(G)| - |E(H)|.
[ 系 ] マトロイド M = (M, ρ) について次は同値。
(1) E は k 個の独立集合の合併.
(2) ∀A ⊂ E ,kρ(A) ≧ |A|.
(∵) M の k 個のコピーの合併のランク関数を ρ~ とすると
|E| = ρ~(E)
= min {ρ(A) + ρ(A) + . . . + ρ(A) + |E - A| | A ⊂ E } ゆえ。 //
[ 系の系 ] グラフ G について次は同値。
(1) E(G) は k 個の極大森の合併.
(2) ∀H ⊂ G ,k dim Z*(H) ≧ |E(H)|.
[ 系の系 ] グラフ G について次は同値。
(1) E(G) は k 個の補森の合併.
(2) ∀H ⊂ G ,k dim Z(H) ≧ |E(H)|.
[ 系の系の系 ] 3 辺連結グラフの辺集合は3つの補木の合併である。( Jaeger 1975 )
[ 系の系の系の系 ] Jaeger の定理.
(∵) G をブリッジをもたないグラフとする。G は連結として示せばよい。
G にサイズが2のコサーキットがあれば分断を繰り返すことにより 3 辺連結のケースに帰着される。
E(G) = N1c ∪ N2c ∪ N3c ( Ni は生成木 ) とすると
E(G) = z(N1) ∪ z(N2) ∪ z(N3) となる。 //
同様の技法で次の結果も得られている。
[ 定理 12.11 ] 4 辺連結グラフの辺集合は2つの補木の合併である。( Jaeger )
[ 系 ] 4 辺連結グラフの辺集合は2つのサイクルで cover できる。
Jaeger は平面性という条件ぬきで補木による被覆というカタチで4色問題に大きな足跡を残したことになるが、4色問題解決までには到らなかった。4色問題がどのような天才によってどのようなカタチで解決されるのか甚だ興味のあるところである。
マトロイドは数学の背景にあって論理的な基礎を支えるだけでなく組み合せ論などでは具体的にもかなり有効である。しかし扱いやすい代数演算が欠如しているのが弱点といえる。
本講義ではグラフをハイパーグラフの特別な場合として定義してその数学的な基礎やいくつかのトピックスについて述べてきた。
ハイパーグラフは多重度を考慮した集合族と考えられるが、特別なグラフである2部グラフはそのような集合族を決め、また逆も成り立つ。
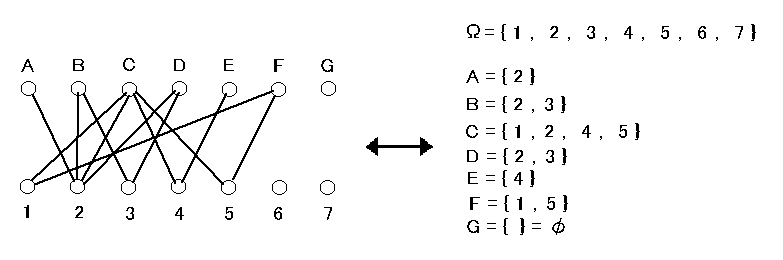
このことから、グラフ理論は(有限)集合族の理論と強い相関をもっていることがうかがえる。
実際、たとえば、マッチングに関する Hall の定理は次のように集合族の定理に翻訳できる。
空でない有限集合の族 A1, A2, . . . , An ( n≧1 ) に対して si ∈ Ai ( 1≦i≦n ) である相異なる元の集合 { s1, s2, . . . , sn } を 横断(transversal)という。
[ Hall の定理 ] 空でない有限集合の族 A1, A2, . . . , An ( n≧1 ) が横断をもつ
⇔ 1≦k≦n のかってな k について、どの k 個の Ai の合併もサイズが k 以上.
重要だと思われるので、今少しこの方向での集合族の扱いについて述べておこう。
以下、集合族やその要素である集合(≠φ)は有限とする。
集合族 S は重複も許したものとする。
重複を考慮した S の要素の個数を |S| で表示する。
∪S を S の 台 とよぶ。
集合族 S に対してその 特性数(オイラー標数) ch(S) を
ch(S) = |∪S| - |S|
と定義する。
また S の ランク( もしくは 自由度 ) r(S) を
r(S) = minφ≠X⊂S ch(X)
と定義する。( r(φ)は不定.) r(S) を rk(S) とも書く。
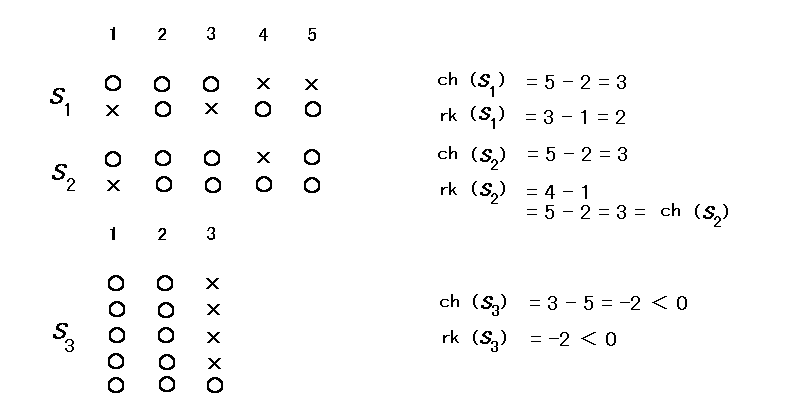
2つの集合族 S1, S2 に対して、
S1∪S2 は重複度は max をとる合併
S1∩S2 は重複度は min をとる共通部分
とする。( max(p, q) = p + q - min(p, q). )
[ 定理 13.1 ] ch(S1∪S2) = ch(S1) + ch(S2) - (|(∪S1)∩(∪S2)| - |S1∩S2|)
≦ ch(S1) + ch(S2) - ch(S1∩S2).
とくに、 S1∩S2 = φ ⇒ ch(S1∪S2) ≦ ch(S1) + ch(S2).
また、(∪S1)∩(∪S2) = φ ⇒ ch(S1∪S2) = ch(S1) + ch(S2).
S の各要素の k 元部分集合からなる族( k 制限 )τ で r(τ) ≧ k-1 であるものを S の k 横断 とよぶことにする。
[ 定理 13.2 ] 集合族 S と非負の整数 k に対してつぎは同値。( Hall の定理の拡張 )
(1) S は k 横断をもつ.
(2) S はかってな t 制限( 0≦t≦k-1 )の拡張である k 横断をもつ.
(3) r(S) ≧ k - 1.
S の空でない部分族 F が S の ファクター :⇔ ch(F) = r(S) ( 注: いわゆるファクター(因子)とは無関係 )
[ 定理 13.3 ] S のファクター F1, F2 が F1∩F2 ≠ φ のとき F1∪F2 も F1∩F2 もファクターである。
<証明> r(S) = k とする。
ch(F1) = ch(F2) = k で、定理 11.1 より、
k ≦ ch(F1∪F2)
≦ k + k - ch(F1∩F)
≦ k + k - k = k
∴ ch(F1∪F2) = ch(F1∩F2) = k. //
[ 系 ] 異なる2つの極小ファクターは互いに素である。また、異なる2つの極大ファクターも互いに素。
[ 系 ] 自己 k 横断(自分自身の k 横断)はいくつかの極大ファクターの素和である。
[ 定理 13.4 ] F1, F2 が F1∩F2 ≠ φ であるような自己ファクターのとき F1∪F2 も 自己ファクターである。
[ 系 ] 任意の集合族 S はいくつかの極大な自己ファクターの素和である。(分割定理)
( S の部分 )族 C が k サーキット :⇔ C は空でなくて、 ch(C)≦ k となる極小なもの。
定義中の ≦ は = になる。
(∵) |∪(C - {X})| - |C - {X}| ≧ k + 1
|∪(C - {X})| - |C| ≧ k ≧ |∪C| - |C|
∴ |∪(C - {X})| - |C| ≧ |∪C| - |C|
一方 |∪(C - {X})| - |C| ≦ |∪C| - |C| ∴ |∪(C - {X})| - |C| = |∪C| - |C|. //
S の k サーキットの全体を Ck(S) で表示する。
[ 注 ] S が k サーキットを含まない ⇔ r(S) ≧ k + 1.
よって定理 13.2 の条件(3)は S が k-2 サーキットを含まないということを意味している。
[ 定理 13.5 ] [S , Ck(S)] は重複も考慮したマトロイドを成す。
<証明> 空集合 φ は Ck(S) の要素ではない。
(C1) あきらか。
(C2) C1, C2 を異なるサーキットで C1 ∩ C2 ≠ φ とする。
任意の X ∈ C1 ∩ C2 に対してある k サーキット C が存在して C ⊂ (C1 ∪ C2) - {X} が言えればよい。
|∪(C1 ∪ C2)| ≦ |∪C1| + |∪C2| - |∪(C1 ∩ C2)|
≦ |C1| + k + |C2| + k - (|C1 ∩ C2| + k + 1)
≦ |C1 ∪ C2| + k - 1.
∴ |∪(C1 ∪ C2)| ≦ |C1 ∪ C2| + k - 1
∴ |∪((C1 ∪ C2) - {X})| ≦ |(C1 ∪ C2) - {X}| + k.
C としては (C1 ∪ C2) - {X} の中で不等号を保持する極小なのをとればよい。 //