《 一筆書き 》
グラフ G の頂点と辺の交互列 v0e0v1e1 . . . ek-1vk は ei = {vi, vi+1} ( i ≦ k - 1 )であるとき G における長さ k の 歩道(walk)とよばれる。 v0 = vk のときは 閉歩道 という。
グラフのすべての辺をちょうど1回ずつ通る閉歩道を オイラー周遊路 とよぶことにする。オイラー周遊路をもつグラフを オイラーグラフ(Euler graph, eulerian graph)という。
次の定理は「はじめに」の図にあるケーニヒスベルクの橋にまつわる問題
” 図の7つの橋をちょうど1回ずつ渡って元の地点に戻ってくるような径路はあるか? ”
に関連してオイラーが見出したもので、「グラフ理論の起源である」といわれている。(これに関しては異論があるが、グラフ理論が「役に立つ」ことを示した最初の例とは言えるかもしれない.)
[ 定理 ] 連結グラフ G について、オイラーグラフ ⇔ 偶グラフ.( Euler 1736 )
<証明> 必要性はあきらか。
十分性; G を偶グラフ, W = v0e0v1 . . . ek-1vk を2回以上通る辺を含まない歩道のうちで最長のものとする。
W の最長性から、W は vk と接合する辺をすべて含んでいる。
vk に接合するリンクは偶数本なので、vk = v0 が必要で W は閉歩道であることになる。
W がオイラー周遊路でないと仮定する。
G が連結であることから、G には W に含まれないで W の頂点に接合する辺 e が存在する。
e = uvi とすると、歩道 ueviei . . . ek-1vke0 . . . ei-1vi は2回以上通る辺を含まない W より長い歩道となり矛盾。 //
点集合 S はあるグラフ G の描画を点集合としたものになっているとき 線系 とよぶことにする。G を S の 台グラフ とよぶ。
[ 系 ] 線系 S について次は同値である。
(1) 一筆書きできる.
(2) 連結でどの台グラフも奇点が2個以下.
《 Grinberg の定理 》
ここでは単純閉曲線 J の内部の閉包を Int J, 外部の閉包を Ext J で表すことにする。
[ 定理 ] ハミルトンサーキット C をもつ平面グラフ G について、
Σi=1ν (i - 2)(φ'i - φ''i) = 0.
但し、ここで φ'i と φ''i はそれぞれ Int C と Ext C に含まれる次数 i の面の数とする。( Grinberg 1968 )
<証明> Int C に含まれる E(G) - C の要素の全体を E' として ε' = |E'| とおく。このとき Int C は丁度 ε' + 1 個の面を含む。(図を見よ。)
E' の各辺は Int C に含まれる2つの面の境界上にあり C の各辺は Int C に含まれる丁度ひとつの面の境界上にある。
∴ Σi=1ν iφ'i = 2ε' + ν (**)
(*)と(**)より
Σi=1ν (i - 2)φ'i = ν - 2
同様にして
Σi=1ν (i - 2)φ''i = ν - 2
よって定理の式を得る。 //
今までの所論からハミルトンサーキットの概念は中間的な概念で一般性をもってないと考えられるが、歴史的には次の予想もハミルトンサーキットファンを増加させた一因のようである。
Tait 予想 3 正則 3 連結平面グラフはハミルトンサーキットをもつ。
この予想の反例は Tutte により構成されたが、Grinberg は別の反例を構成した。
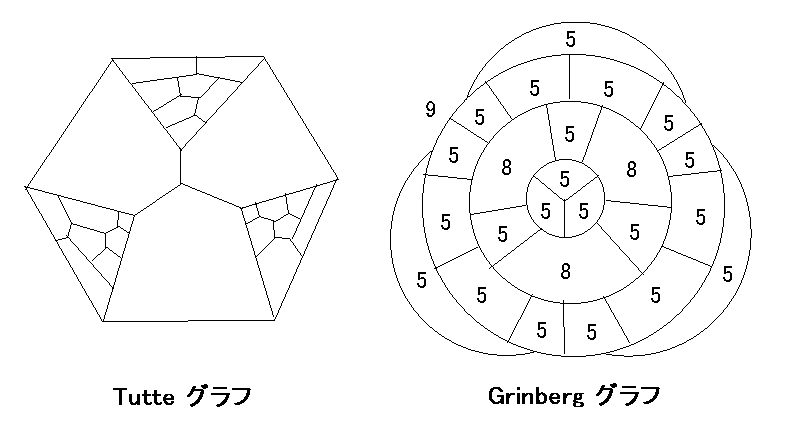
(5 - 2)(φ'5 - φ''5) + (8 - 2)(φ'8 - φ''8) + (9 - 2)(φ'9 - φ''9) = 0
∴ 7(φ'9 - φ''9) ≡ 0 (mod 3)
図のように平面グラフとして表現しておくと 7(φ'9 - φ''9) = 7(0 - 1) = - 7 であるから不合理。 //
<Tutte グラフがハミルトンサーキットを持たない理由> Tutte グラフ G がハミルトンサーキット C をもつとする。
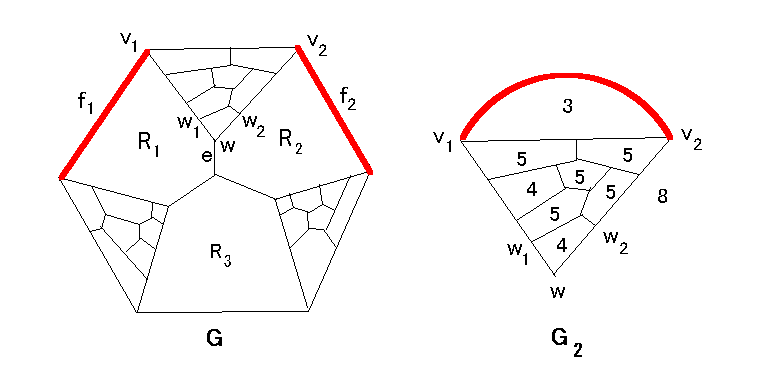
よって R1, R2, R3 のうち高々1個のみが C の外部にあり、少なくとも2つたとえば R1 と R2 が C の内部にあることになる。すると e は C に属さないことになるので C は f1, f2 を通る。また、C に含まれる v1v2 パス P で G1 のハミルトンパスであるのが存在することになる。
G - {e, f1, f2} の連結成分で w を含むのを G1 とする。
グラフ G2 = G1 + v1v2 は C2 = P ∪ {v1v2} をハミルトンサーキットとしてもつ。
Grinberg の定理を G2 と C2 に適用すると
1(φ'3 - φ''3) + 2(φ'4 - φ''4) + 3(φ'5 - φ''5) + 6(φ'8 - φ''8) = 0
v1v2 は C2 の辺で G2 の無限領域は C2 の外部にあることから
φ'3 - φ''3 = 1 - 0 = 1 かつ φ'8 - φ''8 = 0 - 1 = -1
∴ 2(φ'4 - φ''4) + 3(φ'5 - φ''5) = 5
ww1 も ww2 も C の辺ゆえ
φ'4 ≧ 1
∴ φ'4 - φ''4 = 1 - 1 = 0 または φ'4 - φ''4 = 2 - 0 = 2
もしも φ'4 - φ''4 = 0 だと 3(φ'5 - φ''5) = 5 で不可能。
また、もしも φ'4 - φ''4 = 2 だと 3(φ'5 - φ''5) = 1 でやはり不可能。
よって Tutte グラフは非ハミルトンである。 //
グラフ G のボンド B = δ(X) で <X> も <Xc> も木であるのを ハミルトンボンド とよぶ。( by Tutte )
[ 命題 ] 連結グラフ G のボンド B = δ(X) について次は同値である。
(1) B はハミルトンボンド.
(2) |B| = dim Z(G) + 1.
[ 命題 ] 連結グラフ G がハミルトンボンドをもてば G は 4 染色可。
<証明> G のハミルトンボンドのひとつを δ(X) とする。<X> も <Xc> も木なので2部グラフである。よって 4 染色可。 //
Grinberg の定理は次のように改良される。
[ 定理 ] ハミルトンボンド B = δ(X) をもつグラフについて、
Σi=1ε (i - 2)(ψ'i - ψ''i) = 0.
但し、ここで ψ'i と ψ''i はそれぞれ <X> と <Xc> の G での次数が i の頂点の数とする。
《 トーナメント 》
完全グラフ Kn の向き付けを トーナメント という。(実際、n 人の選手による総当たり戦の結果を表示するとトーナメントが得られる)
[ 定理 ] ループをもたない有向グラフ D は長さ χ(D) - 1 の有向パスをもつ。( Roy, Gallai )
<証明> A' を D' = D - A' が有向サーキットをもたないような極小な D の弧の集合とし、D' における有向パスの長さの最大値を k とする。
D' の点 v に対して、始点を v とする有向パスの長さの最大値が i - 1 のとき点 v を色 i で着色する。この着色で色が i の点全体を Vi としよう。
P を D' 内の正の長さの有向 uv パス,v ∈ Vi とする。このとき D' 内に v1 = v の有向パス Q = v1v2 . . . vi がある。
D' は有向サーキットをもたないから合成したパス PQ は長さが i 以上の有向パスで u は Vi には属さない。
D のかってな弧 uv をえらぶ。
uv が D' の弧のとき; uv は長さ 1 で正の長さをもつから u と v は異なる色で着色されている。
uv が D' の弧でないとき; uv ∈ A' で A' の極小性から D' + uv は有向サーキット C をもつ。 C - uv は D' 内の有向 vu パスゆえ v と u は異なる色である。
よって V1, V2, . . . , Vk+1 は D の (k + 1) 染色で χ(D) ≦ k + 1.
したがって D は長さ χ(D) - 1 以上の有向パスをもつ。 //
[ 系 ] トーナメントは有向ハミルトンパスをもつ。( Redei )
有向グラフ D に有向 uv パスがあるとき点 v は点 u から 到達可能 という。
有向グラフ D の2点はそのどちらからも到達可能なとき 強連結(である)とよび、どの2点も強連結であるような有向グラフを 強連結有向グラフ という。
有向グラフ D の点 v に対して、{ u ∈ V(D)| (u, v) ∈ A(D) } を v の 入近傍 とよび ND-(v) , { u ∈ V(D)| (v, u) ∈ A(D) } を v の 出近傍 とよび ND+(v) で表す。
[ 定理 ] ループをもたない有向グラフ D は独立集合 S で S に属さない D の各点が長さが高々 2 の有向パスによって S の1点から到達可能であるようなのをもつ。( Chvatal and Lovasz )
<証明> 頂点の数 ν に関するインダクションで示す。
ν = 1 のときあきらかに成り立つ。
ν より少ない頂点数の有向グラフについて成り立つとする。(ν ≧ 2 )
v を D のかってな点とする。帰納法の仮定により D' = D - ({v} ∪ N+(v)) の中には独立集合 S' で S' に属さない D' の各点が長さ高々 2 の有向パスで S' の1点から到達可能なのがある。
v が S' のある点 u の出近傍に属するとき; N+(v) の各点は長さ2の有向パスで u から到達可能なので S = S' とすれば良い。
v が S' のどの点の出近傍にも属さないとき; v と S' は非隣接ゆえ S = S' ∪ {v} とすれば良い。 //
有向グラフの頂点はどの頂点へも長さが高々2の有向パスで到達できるとき キング とよばれる。
[ 系 ] トーナメントはキングをもつ。(有名定理)
<直接証明> v を出次数が最大の頂点とする。v がキングでないとすると長さが高々2の有向パスで到達できない頂点 w があることになる。
すると N+(w) ⊃ N+(v) ∪ {v} が必要なので w の出次数のほうが大きくなり不合理である。 //
長さが k のサーキットを k サーキット という。
[ 定理 ] 頂点数 n が3以上の強連結トーナメント D の各点は 3 ≦ k ≦ n の各 k に対してある有向 k サーキットの中に含まれる。( Moon )
<Sol> u を D のかってな点とする。
D が強連結であることから O(u) も I(u) も空ではなく、また O(u) から I(u) への弧が存在しなければならない。このことから u はある有向 3 サーキットに含まれることはただちにわかる。
3 ≦ s < k の s に対して u はある有向 s サーキット C の中に含まれると仮定する。
C = (v0, v1, . . . , vs) ( 但し v0 = vs = u )とする。
もし V(D) - V(C) の点 v で v から V(C) に行く弧も V(C) から v に来る弧もあるのが存在すればある i があって vi v も v vi + 1 も D の弧であり u は (s + 1) サーキット (v0, v1, . . . , vi, v, vi + 1, . . . , vs) に含まれている。
そうでないとき、S を V(D) - V(C) の V(C) から来る点全体,T を V(D) - V(C) の V(C) へ行く点全体とする。
D が強連結なことから S, T は空でなく、また S から T への弧も存在する。 v w を S から T への弧とすると u は (s + 1) サーキット (v0, v, w, v2, . . . , vs) に含まれている。 //
[ 系 ] 強連結トーナメントは有向ハミルトンサーキットをもつ。( Camion )
《 Cayley の定理 》
[ 定理 ] 完全グラフ Kn の生成木の総数 τ(n) は nn-2である。( Sylvester 1857 Cayley 1889 )
<証明> 1点vをえらび、その次数が k であるような生成木の総数を τ(n,k) で表示する。
A を deg(v) = k - 1 である生成木とする。v に接合していない辺 wz を A から除去して2つの部分木に分離したとき、z が v とは非連結になるとする。
辺 vz を付加すると deg(v) = k なる木 B がえられる。
このとき、生成木のペア (A, B) を「連鎖」(linkage)とよぶことにする。
一方、B を deg(v) = k の生成木とし、B - v の連結成分を T1, . . . , Tk とする。
B から v に接合する辺 vwi( wi∈V(Ti) )を除去し Ti 以外の Tj に属する勝手な頂点 u と wi を辺で結ぶと deg(v) = k - 1 である生成木 A がえられる。
このとき (A, B) は連鎖であり、かつまたすべての連鎖はこのようにして得られる。
B の選び方は τ(n, k) 通りあり、点 wi と Tj の点との結び方は (n-1) - ni 通り( ni は Ti の頂点数 )ある。
よって連鎖 (A, B) の総数は
τ(n, k){(n - 1 - n1) + . . . + (n - 1 - nk)} = (n - 1)(k - 1)τ(n, k)
である。
∴ (n - k)τ(n, k-1) = (n - 1)(k - 1)τ(n, k)
これと τ(n, n-1) = 1 より τ(n, k) = n-2Ck-1(n - 1)n-k-1.
∴ τ(n) = Σk=1n-1 τ(n, k)
= Σk=1n-1 n-2Ck-1(n - 1)n-k-1
= Σk=0n-2 n-2Ck(n - 1)(n-2)-k
= {(n - 1) + 1}n-2
= nn-2. //
<別証1> V(Kn) = [n] = { 1 , 2 , . . . , n } とする。
[n] から作れる長さ n - 2 の数列の数は nn-2 ゆえ、Kn の生成木全体の集合と [n] から作れる長さ n-2 の数列全体の集合の間の1対1対応を示せばよい。
<別証2>( Joyal ) 頂点の順序対 (u, v) を指定した生成木 T = (T; u, v) は n2 τ(n) 個存在する。
また、写像 f: [n] → [n] は nn 個存在する。
∴ τ(n) = nn-2. //
[ 系 ] 頂点数が n の木の与えられた頂点が端点である確率 P(n) とすると lim P(n) = 1/e となる。
(∵) τ(n, 1) = (n - 1)n-2
∴ P(n) = (n - 1)n-2/nn-2 = ((n - 1)/n)n-2
∴ lim P(n) = lim (n/(n - 1))-n+2
= lim [{(1 + 1/(n - 1))n-1}-1 n/(n - 1)]
= 1/e . //
グラフ G の頂点が {1, 2, . . . , n} でラベル付けされているとき、頂点 i と j を結ぶ辺の本数を ij 要素とした n×n 行列 A(G) を G の 隣接行列(adjacency matrix)という。( 対称でトレースはループの本数となっている。 )
ij 要素を i = j のとき頂点 i の次数、i≠j のとき 0 とした n×n 行列 D(G) を G の 次数行列 という。
n×n 行列 D(G) - A(G) を G の ラプラス行列(laplacian matrix)または ラプラシアン とよび L(G) で表示する。
[ 定理 ] ループをもたないグラフ G に対して L(G) の i 行と i 列を除去して得られる (n-1)×(n-1) 行列 Li(G) の行列式は τ(G) に等しい。(行列木定理(Matrix-Tree Theorem))
例 図のグラフ G は K2,3 の頂点を {1, 2, 3, 4, 5} でラベル付けしたものであり |L1(G)| = 12 = 3×23-1 となっている。
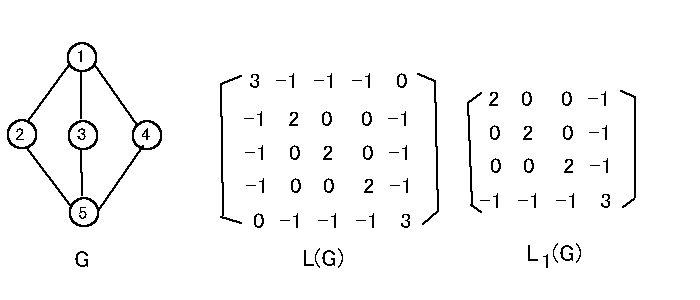
[ 定理 ]
τ(Qn) = ( 2 の (2n - n -1) 乗 ) × Πi=1n ( i の nCi 乗 ). ( Stanley )
《 Hajos の合併 》
グラフ G ,H に対して、uv ∈ E(G) ならば f(u)f(v) ∈ E(H) となる写像 f: V(G) → V(H) を G から H への 準同型(homomorphism)という。
[ 補題 ] K≠φ を次の条件をみたす単純グラフの集まりとする。
(ⅰ) G ∈ K で G から H への準同型がある ⇒ H ∈ K.
(ⅱ) G をグラフ、a, b, c ∈ V(G) を a adj c だが a と b ,b と c は非隣接な3頂点とするとき、
G + ab ∈ K , G + bc ∈ K ⇒ G ∈ K
このとき、k ≧ 0 が存在して K は k 染色不可能なグラフ全体の集まりである。
<証明> G に辺を付加していっても K に属するので K は完全グラフをひとつは含む。Kk+1 を K 内の最小の完全グラフとする。
G ∈ K で G は k 染色可能とする。
G の k 染色は G から Kk への準同型を定義するから、(1)により Kk ∈ K となる。これは矛盾ゆえ K の要素は k 染色不可能。
G が k 染色不可能で K に属さないと仮定する。
G のどの隣接しない2頂点を結んでも K に属するとしてよい。(∵ ある非隣接な2頂点を結ぶと K に属さないならその操作を繰り返す。|V(G)| を p とすると p ≧ k + 1 で Kk+1 から Kp への準同型があるから Kp ∈ K.よってそのような操作は Kp に達するより前に終わる。)
この G に対して「非隣接」は V(G) 上の同値関係となる。(∵ 反射律,対称律はあきらか。ab も bc も E(G) に属さず ac ∈ E(G) とする。G の極大性から G + ab も G + bc も K に属するので(ⅱ)より G ∈ K.これは矛盾ゆえ推移律も成り立つ。)
V(G) がこの同値関係による類別で m 個の類に分けられるとすると G は k 染色不可能なので m ≧ k + 1.
すると Kk+1 ⊂ Km ⊂ G.
よって K ∋ Kk+1 ⊂ G かつ G は K に属さないということになり(ⅰ)に反する。 //
[ 定理 ] 単純グラフについて次の3つの変形操作を考える。
(α) 辺または点を付加する。( 拡大 )
(β) 2つの非隣接な頂点を1点にまとめる。(平行な辺が生じたら1本だけにする)( 同一視 )
(γ) 2つのグラフ G1,G2 と uivi ∈ E(Gi) ( i = 1, 2 ) に対し、uivi を除去して新しい辺 v1v2 を付加して u1 と u2 を1点にまとめる。( Hajos の合併 )
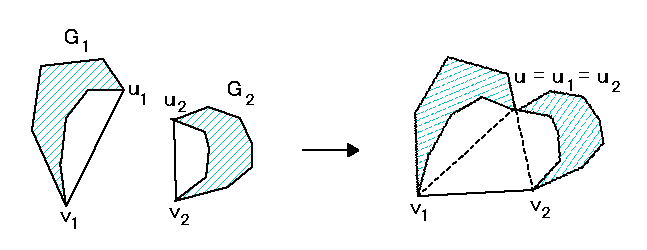
<証明> k 染色不可能なグラフに(α)または(β)を施しても k 染色不可能なことはあきらか。
2つのグラフ G1, G2 から(γ)で得られたグラフを G とする。G が k 染色可能、G1 も G2 も k 染色不可能とする。
G の k 染色によってその部分グラフ G1 - u1v1 も G2 - u2v2 も k 染色されている。
G1, G2 は k 染色不可能ゆえ u1 と u2 を同一視した点 u とすると u と v1, u と v2 は同色であることが必要。すると v1 と v2 が同色なことになり矛盾。
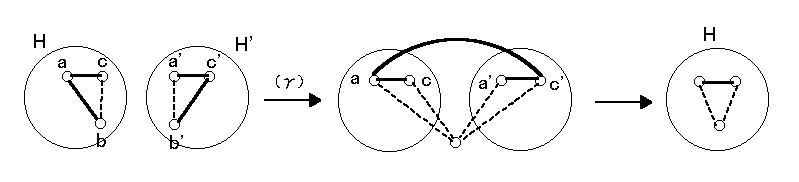
次に K を Kk+1 から(α),(β),(γ)を有限回施すことでえられるグラフ全体の成す集まりとする。
K は補題の(ⅰ)をみたす。(∵ G から H への準同型があれば H は G から(α),(β)の組み合わせでえられる。)
H をグラフ,a, b, c ∈ V(H),a adj c, non(a adj b), non(b adj c) とし、H + ab ∈ K, H + bc ∈ K とする。
また、H' を H のコピーとし、H の頂点 v に対応する H' の頂点を v' とする。 H' + b'c' ∈ K である。
b と b' を同一視して ac' を付加し ab と c'b' を除去する。更にすべての v ∈ V(H) に対して v と v' を同一視して多重辺が生じたら1本の辺にする。このようにすると H がえられるから H ∈ K. よって K は(ⅱ)もみたす。
《 染色多項式 》
グラフ G の異なる k 染色の数を PG(k) または P(G ; k) で表す。
例 (p, 0) グラフ G に対して P(G; k) = kp. P(Kp ; k) = k(k - 1) . . . (k - p + 1).
[ 定理 ] 単純グラフ G のかってな辺 e に対して P(G; k) = P(G - e; k) - P(G/e; k).
<証明> 意味を考えると P(G - e; k) = P(G; k) + P(G/e; k) となっているから。 //
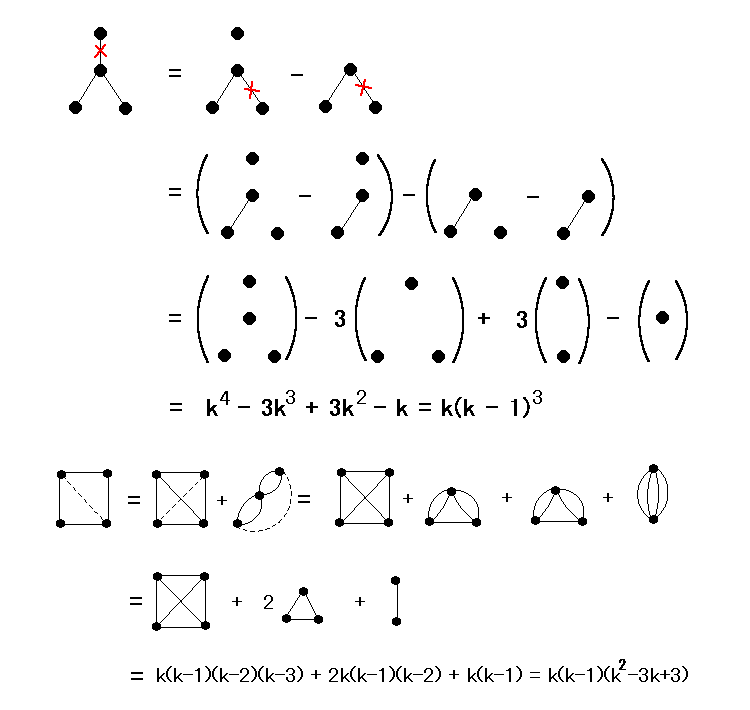
(1) P(G; k) は p = |V(G)| 次の k についての整数係数多項式で、最高次の係数は 1 ,定数項は 0 である。
(2) P(G; k) の係数は交互に符号が交代する。
(3) P(G; k) = ΣS⊂E(G) (-1)|S|kω(S).但し、ω(S) = ξ(G - Sc).
<証明> 辺数についてのインダクションでまず(1)と(2)を示す。G は平行な辺をもたないとして良い。
辺数が 0 のときは P(G; k) = kp で題意をみたしている。
辺数が m 未満のグラフについて成り立つと仮定する。
G を m 本の辺をもつグラフとする。( m ≧ 1 ) e を G のかってな辺とする。
帰納法の仮定から、P(G-e; k) = Σi=1p-1 (-1)p-iaiki + kp,
P(G/e; k) = Σi=1p-2 (-1)p-i-1biki + kp-1
となる非負整数 a1, a2, . . . , ap-1 および b1, b2, . . . , bp-2 がある。
∴ P(G; k) = Σi=1p-2 (-1)p-i(ai + bi)ki - (ap-1 + 1)kp-1 + kp.
(3) (合併集合のサイズについての)包除原理による。 //
P(G; k) を G の 染色多項式(chromatic polynomial)という。( by Birkhoff )
[ 定理 ] P(G; k) = 0 の実数解は ν(G) 以下である。( Lovasz )
《 Tutte 多項式 》
グラフに単位元を持つ可換環 R の要素を与える関数は同型なグラフには同じ要素を与えるとき( R での )グラフ不変量 または単に 不変量 とよぶ。
グラフ G に対して次の性質により決まる2変数整数係数多項式 T(G; x, y) を Tutte 多項式 という:
G が辺をもたないとき T(G; x, y) = 1 で、
T(G; x, y) = x T(G / e; x, y) , e がブリッジのとき
T(G; x, y) = y T(G - e; x, y) , e がループのとき
T(G; x, y) = T(G - e; x, y) + T(G / e; x, y) , otherwise
[ 定理 ]
(1) T(G; x, y) は上記の条件から矛盾なく定まる Z[x, y] での不変量で非負係数をもつ。
(2) T(G; x, y) = ΣA⊂E(G) (x - 1)r(E(G)) - r(A)(y - 1)|A| - r(A).
例 k 個の辺をもつ森の Tutte 多項式は xk.
[ 定理 ] Z[x, y] での不変量 f が次の漸化式をみたすとする:
G が辺をもたないとき f(G) = 1 で、
f(G) = x f(G / e) , e がブリッジのとき
f(G) = y f(G - e) , e がループのとき
f(G) = a f(G - e) + b f(G / e) , otherwise
このとき f(G) = a|E| - r(E)br(E) T(G; x/b, y/a) である。(レシピ定理)
有向サーキットが生じないような向き付けを 非輪状な向き付け という。
[ 定理 ]
(1) T(G; 2, 2) = 2ε(G).
(2) グラフ G の極大森の数 τ(G) は T(G; 1, 1).
(3) グラフ G の森の数は T(G; 2, 1).
(4) 連結グラフ G に対して、辺の集合 A で G|A が連結であるのの数は T(G; 1, 2).
(5) グラフ G の非輪状な向き付けの数は T(G; 2, 0).( Stanley 1973 )
(6) P(G; k) = kξ(G) (- 1)r(E(G)) T(G; 1 - k, 0).
<証明> (3); G の森の数 a(G) とする。
G が辺をもたないとき森は空集合のみなので a(G) = 1 である。
e がブリッジのとき、G の e を含む森と G の e を含まない森は数が等しく、ともに a(G / e) である。 ∴ a(G) = 2 a(G / e).
e がループのとき e を含む森はなくて a(G) = a(G - e) ∴ a(G) = 1 a(G - e).
e がブリッジでもループでもないとき、e を含まない森の数は a(G - e),e を含む森の数は a(G / e) なので a(G) = a(G - e) + a(G / e).
以上より a(G) = T(G; 2, 1).
(5); G の非輪状な向き付けの数を A(G) で表す。
G が辺をもたないとき、A(G) = 1 である。
G がブリッジ e をもつとき、G/e のどの向き付けも e をどちらに向き付けても G の向き付けに拡張できるので、A(G) = 2 A(G/e).
G がループ e をもつとき、あきらかに A(G) = 0.
G がブリッジでもループでもない辺 e をもつとき; e の端点を u, v とする。
G - e の向き付けは次の3つのタイプに分けられる。
タイプ1. u から v への有向パスをもつもの
タイプ2. v から u への有向パスをもつもの
タイプ3. u から v への有向パスも v から u への有向パスももたないもの
それぞれのタイプの向き付けの数を ai とすると、
A(G - e) = a1 + a2 + a3 ,
A(G) = a1 + a2 + 2 a3 ,
A(G / e) = a3
であることが容易に示せるので A(G) = A(G - e) + A(G / e) をえる。
以上から A(G) = T(G; 2, 0) である。
(6); f(G; k) = P(G; k) / kξ(G) がレシピ定理における漸化式を a = 1,b = - 1,x = k - 1,y = 0 でみたしていることを示せばよい。
G が辺を持たないときは, ξ(G) = |V(G)| であるが, P(G; k) = kξ(G) なので f(G; k) = kξ(G) / kξ(G) = 1.
e を G のループとすると P(G; k) = 0 だから f(G; k) = 0.
次に e を G のブリッジとする。G - e の連結成分を二分してできる部分グラフ G1 と G2 を e が連結しているようにできる。
このとき P(G; k) = P(G1; k) P(G2; k) (k - 1) / k となる。(∵ G1 と G2 を別個に k 染色することを考える。e の両端が異なる色になる割合は (k - 1) / k である。)
また P(G / e; k) = P(G1; k) P(G2; k) 1/k である。
∴ P(G; k) = (k - 1) P(G / e; k).
∴ f(G; k) = (k - 1) P(G / e; k).
最後に e がブリッジでもループでもない G の辺であるときは、
P(G; k) = P(G - e; k) - P(G / e; k) より f(G; k) = f(G - e; k) - f(G / e; k).
(1),(2),(4)は各自確められたい。 //
《 Kuratowski の定理の証明 》
ここでは Thomassen により簡易化された定理 10.2(Kuratowski の定理)の証明を紹介する。Tutte による 3 連結単純平面的グラフの凸描画可能性の定理も同時に示される。
K5 もしくは K3, 3 の細分であるような部分グラフを Kuratowski 部分グラフ とよぶ。
どの真部分グラフも平面的であるような非平面的グラフを 極小非平面的グラフ(minimal nonplanar graph)という。
補題 1 極小非平面的グラフは 2 連結である。
<証明> G を極小非平面的グラフとする。
G が非連結であれば各連結成分は平面的で G も平面的となり不合理なので G は連結とする。
G が切断点 v をもったとすると G - v の連結成分と v で誘導される G の部分グラフ G1, G2, . . . , Gk は平面的である。これらを放射状に実現できるので G も平面的となりやはり不合理。 //
補題 2 S = {x, y} が G の分離集合、G1 と G2 が G1 ∪ G2 = G, V(G1) ∩ V(G2) = S であるような G の部分グラフとする。また Hi = Gi + xy とする。
このとき G が非平面的ならば H1 もしくは H2 も非平面的である。
<証明> H1 も H2 も平面的とする。
辺 xy は H1 の非有界な面の境界に含まれるような H1 の平面的実現が存在する。(∵ 球面へ射影して平面に射影し直せばよい。)
すると、辺 xy で H2 の平面的実現と接着して H2 のひとつの面におさまるようにし必要なら辺 xy を除去することで G の平面的実現が得られてしまうので不合理。 //
補題 3 G が Kuratowski 部分グラフをもたない非平面的グラフでそのようなグラフのうちで最小の辺数をもつとすると、G は 3 連結である。
<証明> 辺を除去しても Kuratowski 部分グラフをもち得ないので G の仮定から辺を除去すると平面的グラフになるので G は極小非平面的で、また補題 1 により 2 連結。
G がサイズ 2 の分離集合 S = {x, y} をもったとする。
G は非平面的ゆえ補題 2 により H1 もしくは H2 も非平面的であるから、ここでは H1 が非平面的とする。
H1 は G より辺数が少ないので G の仮定から H1 は Kuratowski 部分グラフをもたねばならない。
G は辺 xy は含まないかも知れないが H1 - xy は G に含まれている。
H1 の Kuratowski 部分グラフにおける辺 xy の役割は H2 の xy パスで代用できるので G は Kuratowski 部分グラフをもつことになり不合理。 //
Kuratowski の定理を証明するためには、あと Kuratowski 部分グラフをもたない 3 連結グラフは平面的ということを示せば十分である。
補題 4 頂点数が5以上のどんな3連結グラフ G も、G/e がやはり3連結となるような辺 e をもつ。( Thomassen の定理 )
<証明> これは9章の演習問題の8である。 //
次数が3以上の頂点を 分岐点(branch vertex)とよぶことにする。
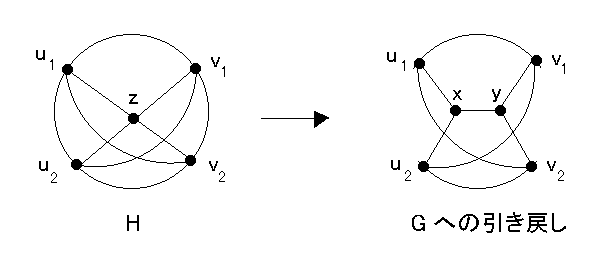
補題 5 G/e が Kuratowski 部分グラフをもつとき G も Kuratowski 部分グラフをもつ。
<証明> H を G/e の Kuratowski 部分グラフ、z を e = xy を縮めて得られる G/e の頂点とする。
もしも z が H の分岐点でなければ、必要であれば z を辺 xy に引き伸ばして G の Kuratowski 部分グラフがえられる。
また、z が H の分岐点で H の中で z に接合している辺が G の中では x か y に高々1本しか接合していないときも同様にして G の Kuratowski 部分グラフがえられる。
残るケースは H が K5 の細分で z が H の分岐点かつ x と y がいずれも z に H で接合している4本の辺のうち2本ずつと G の中で接合しているときである。
u1 と u2 を z から G の中で x に接合する辺を含むパス上をたどって最初に到達する H の分岐点とし v1 と v2 を z から G の中で y に接合する辺を含むパス上をたどって最初に到達する H の分岐点とする。
u1u2 パスと v1v2 パス を H から除去して図のように G に含まれる K3, 3 の細分がえられる。
各辺が直線分で有界な面がいずれも凸であるような平面的実現を 凸実現 もしくは 凸描画 とよぶ。
[ 定理 ] Kuratowski 部分グラフをもたない 3 連結単純グラフは凸描画できる。
<証明> ν(G) についての帰納法で示す。
たかだか4頂点をもつ 3 連結単純グラフは K4 だけで凸描画できるので ν(G) ≧ 5 とする。
e = xy を補題 4 で保証された辺とし v を e の縮約で生じる頂点とする。
補題 5 により G/e も Kuratowski 部分グラフをもたないので帰納法の仮定として H = G/e は凸描画できるとしてよいからそのような描画で考える。
z に接合する辺をすべて除去してえられるグラフはバウンダリーが z を囲む面をもつ。(そのような面は非有界面でもありうるが。)
その面のバウンダリーを C とする。
x1, x2, . . . , xk を C を反時計回りに見た順での C 上の x の隣接点とする。
C 上の y の隣接点がある i について xi から xi+1 までの C の部分にあれば下図のように G を凸描画できる。
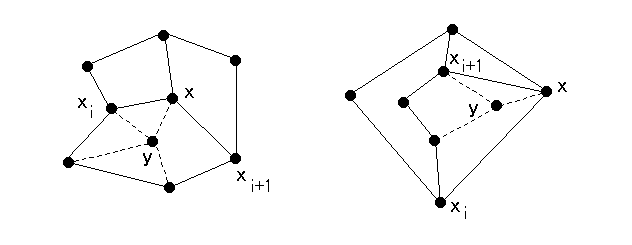
( a ) y は x と C 上で3頂点を共有する
( b ) y はある i について xi と xi+1 を除去してえられる C の部分グラフの別の成分にある C 上の隣接点 u と v をもつ
の2通りである。
( a ) の場合は C と x から C への3本の辺と y から C への3本の辺と 辺 xy とで K5 の細分が構成されてしまう。
( b ) の場合は C とパス u y v とパス xi x xi+1 と辺 xy とで K3, 3 の細分が構成されてしまう。
《 Pfaffian 向き付け 》
ここでは表題の向き付けが可能なグラフの完全マッチングの数を与える Kasteleyn の公式を紹介する。
ここでのグラフ G は単純グラフであるものとし V(G) = [n] = {1, 2, . . . , n} とする。
サイズが even(偶数)のサーキットを 偶サーキット とよぶ。
グラフ G の偶サーキット C と G の向き付け G→ に対して、C を1周するとき同調する向きの G→ の辺が奇数本であるとき C は G→ において 奇数的に向き付けられている(oddly oriented)とよぶ。( C が偶サーキットであることから C の1周の仕方に依らないことに注意. )
G の向き付け G→ がどんな2つの完全マッチング M, M' についても M ∪ M' のすべてのサーキットを G→ において奇数的に向き付けているとき Pfaffian もしくは 認容的(admissible)という。( M ∪ M' のサーキットは偶サーキットであることに注意。)
G の向き付け G→ に対して n 次の交代行列 As(G→) = ( aij | 1≦i, j≦n ) を
+ 1 . (i, j) ∈ E(G→)
aij = { - 1 , (j, i) ∈ E(G→)
0 , otherwise
で定義し G→ の (交代)隣接行列((skew)adjacency matrix)という。
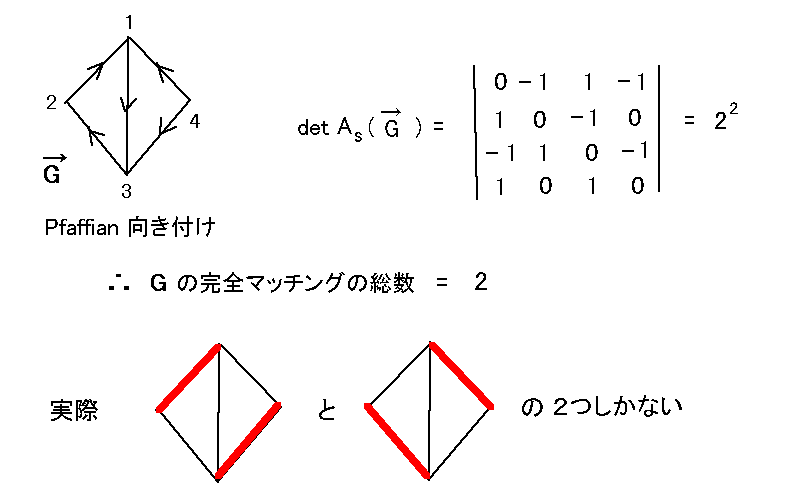
[ 定理 ] G のかってな Pfaffian 向き付け G→ に対して、
( G の完全マッチングの総数 ) = √(det As(G→)). ( Kasteleyn の公式 )
証明の前に少し準備をする。
G の各辺 i j を2つの有向辺 (i, j) と (j, i) に置き換えてえられる有向グラフを ←G→ で表すことにする。
←G→ の長さが偶数のいくつかの有向サーキット( = 有向辺をたどってえられるサーキット )の族 C について G のどの頂点も C の中のちょうどひとつのサーキットに接合しているとき、 C は ←G→ の 偶サーキット被覆(even circuit cover)とよぶ。
[ 補題 ] G の完全マッチングのペア全体と ←G→ の偶サーキット被覆全体とは1対1に対応する。
(∵) この補題の証明は演習に回す。 //
<Kasteleyn の公式の証明> 補題より、det As(G→) が ←G→ の偶サーキット被覆の総数であることを示せばよい。
det As(G→) = Σπ (sgn π) Πi=1n ai, π(i) ( * )
である。
置換 π とその(無駄のない一意的な)巡回置換の積への分解 π = γ1 . . . γk を考える。
各 γj はちょうど Vj ⊂ V(G) に作用しているとすると、対応する積 Πi∈Vj ai, π(i) が 0 でないことと辺の集合 {(i, π(i)) | i ∈ Vj } が ←G→ における有向サーキットであることとは同値である。
よって、( * ) において 0 でない( 1 か -1 の )寄与をする置換全体と ←G→ のサーキット被覆全体は1対1に対応する。
ここでひとつの置換 π と π における長さ奇数の巡回置換 γj を考えてみる。
π' = γ1 . . . (γj)-1 . . . γk とおくと Πi=1n ai, π(i) = - Πi=1n ai, π'(i) であり、更に sgn π = sgn π' である。
よって、π としてはどの γj も長さが偶数の巡回置換であるものだけを考えればよいことがわかった。( ここまでは G→ が Pfaffian ということは使ってない. )
上で確めたことから π は ←G→ の偶サーキット被覆に対応し、補題より、G の完全マッチングのペアに対応する。
G→ が Pfaffian なことから π の巡回置換 γj に対応するサーキット Cj は G→ により奇数的に向き付けられている。
よって、各 γj は Πi=1n ai, π(i) に因数として - 1 寄与し一方 sgn π にも因数として - 1 寄与する。
けっきょく π は ( * ) の和において 1 寄与することになる。 //
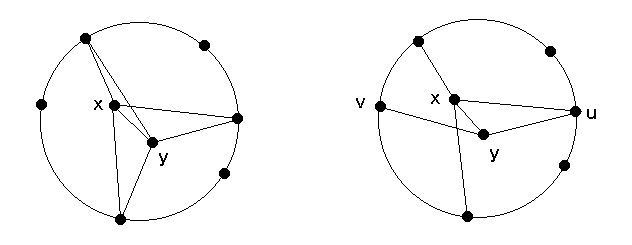
[ 補題 ] 連結平面グラフ G の向き付け G→ が外面を除いた各面のバウンダリーで奇数本の時計回りの辺をもつならば G→ は Pfaffian である。
<証明> まず、各サーキット C に対して時計回りの辺の総数と C の内部にある頂点の総数のパリティー( = 偶奇 )がことなることを示す。
これが示せれば G→ は Pfaffian である。
(∵) G の完全マッチングのペアの合併に含まれるサーキット C の内部に奇数個の頂点があるとすると C の内部の頂点で C の外部の頂点とマッチされてるのが存在することになるがこれは平面性に反する。
よって、C の内部には偶数個の頂点があり、C は時計回りの辺を奇数本もつ。(説明おわり)
G のサーキット C に対して
v = C の内部にある頂点の総数
k = C 上の辺数 = C 上の頂点数
c = 時計回りの C 上の辺の総数
f = C の内部にある面の総数
e = C の内部にある辺の総数
ci = 面 i( i = 1, 2, . . . , f )のバウンダリーに属する時計回りの辺の総数
とおく。
オイラーの公式より、 (v + k) - (e + k) + (f + 1) = 2. ∴ e = v + f - 1.
また、仮定から ci ≡ 1 (mod 2) なので f ≡ Σi=1f ci.
一方、Σi=1f ci = c + e である。(なぜ?)
よって、 f ≡ c + v + f - 1. よって c + v は奇数である。 //
[ 定理 ] どんな平面的グラフも Pfaffian 向き付け可能である。
<証明> G のサーキットランク( = E(G) のサーキットランク )に関する帰納法で示すことにする。連結グラフで示せばよい。
G を連結な平面的グラフとする。
G のサーキットランクが 0 であれば G は木でありかってな向き付けが Pfaffian である。
サーキットランクが n のとき成り立つと仮定。
G をサーキットランクが n + 1 の連結な平面的グラフとする。
G の非有界面のバウンダリーに属する辺のひとつを e とする。
e はブリッジではないから G - e のサーキットランクは n で帰納法の仮定から Pfaffian 向き付けできる。
G - e に e を付加すると有界面がひとつ増えるが、その有界面のバウンダリーが時計回りの辺を奇数本もつように e を向き付けすれば補題により Pfaffian 向き付けがえられることになる。 //
例
[ 演習問題 ] ( → 解答 )
1. 有向グラフについて、強連結であることとかってな V の空でない真部分集合に対してそれを出る弧が存在することは同値であることを証明せよ。
2. 奇サーキットをもつグラフの強連結な向き付けは奇有向サーキットを含むことを示せ。
3. 入次数が 0 の頂点をもたないトーナメント T はキングを3個以上もつことを証明せよ。
4. Cayley の定理を行列木定理から導け。
5. τ(Km , n) = mn - 1 nm - 1 を示せ。
6. P(G; k) の ν(G) - 1 次の係数は -ε(G) であることを示せ。
7. ν(G) = n のグラフ G について次は同値であることを証明せよ。
(1) 木である。
(2) P(G; k) = k (k - 1)n - 1.
8. n 頂点を持つサーキット Cn について T(Cn; x, y) = xn - 1 + xn - 2 + . . . + x + y であることを示せ。
9. 単純な平面的グラフは各辺が直線分であるように平面に辺が交差しないように描画できることを示せ。( Wagner, Fary )
10. グラフ G の完全マッチングのペア全体と ←G→ の偶サーキット被覆全体とは1対1に対応することを示せ。