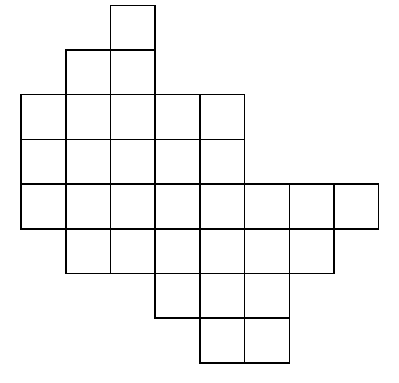ここでは 「グラフ理論の代数化」 についての私案を紹介する。( 数学的対象のタイプの比較にも使える。この章はこういう構造や関連もあるんだと素直に眺めてイメージを膨らませるだけでいいと思う。)
グラフを考えたりグラフを比較するのにフィギュアそのものを見ていたのでは効率が良くない。そういうときの常套手段としてフィギュアに代数構造を対応させるということが考えられる。
よく使われる対応としては、フィギュア A に対してそれと直交する( = even で交わる )フィギュア全体の集合を対応させるという対応がある。副次的にはべき空間 P(E(G)) の部分空間の要素に制限しても良い。
たとえば P(E(G)) の部分空間としてサイクル空間 Z(G) を考えると1辺 e からなるフィギュアにはそれと交わらないサイクル全体が対応し、e がブリッジのときは Z(G) , e がブリッジでないときは Z(G) の n - 1 次元部分空間が対応する。( n は Z(G) の次元 )
しかし、どんな余次元 1 以下の Z(G) の部分空間もそのようにして得られるかというと必ずしもそうではない。
これでは不便なので、まず逆もいえるような対応を見出そう。
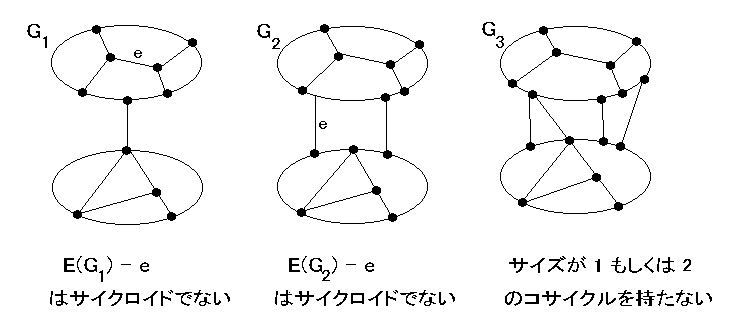
一般にサイズが 1 または 2 のコサイクルを持たないグラフでは、どの辺 e についても γ(e) = E(G) - e ( = E(G) - {e} )はサイクロイドになっている。また、この対応 γ は単射でもある。
後の章で辺集合をいくつかのサイクルで cover する問題を扱うが、その際サイズが 1 のコサイクル(すなわちブリッジ)もしくはサイズが 2 のコサイクルを持つグラフは考慮しなくても良い。(∵ ブリッジはサイクルで cover されないし、サイズが 2 のコサーキットを持つときは図のように分断して考えればよいから。)
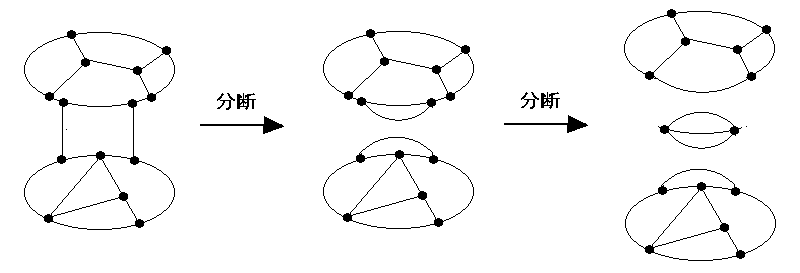
そこで γ(e) に含まれないサイクロイド全体の集合、言い換えると e を要素として含むサイクロイド全体の集合 p(e) を考えてみる。( p はドイツ文字「ペー」のつもり. )
Γ(G) = {γ| γ は G のサイクロイド} は合併演算 ∪ で閉じていて、最小元 0 = φ, 最大元 ∞ = { e ∈ E(G) | e は非ブリッジ } をもつ可換ベキ等半群となっていて p(e) はその部分半群となっている。(ベキ等というのは、γ∪γ=γ ということで、半群というのは ∪ が結合法則をみたすこと.)
実は更に特徴的な部分代数系となっている。
少し半群論の用語について述べておこう。( 半群論についてはかなり自己流なので正規の用語法と違ってるかも知れないので注意. )
以下、半群としては可換な半群のみを考える。
半群 S = (S, +) の部分半群 I は吸収的( 即ち a ∈ I, b ∈ S ⇒ a + b ∈ I )なとき イデアル という。
イデアル I が a + b ∈ I であれば a ∈ I または b ∈ I をみたすとき 素イデアル(prime ideal)とよぶ。
空集合を除いて包含関係で極小な素イデアルを 原子的(atomic)とよぶ。
可換ベキ等半群は γ≦δ を γ+δ=δ と定めるとポセットとなる。
{ε∈Π| γ≦ε≦δ } を [γ, δ] とかく。
最小元 0 , 最大元 ∞ をもつ可換ベキ等半群 Π を プリズム(prism)とよぶことにする。
例 群 G の部分群全体(の集合)は ∩ でプリズム。0 = G , ∞ = (eG) .
位相空間 X の開集合全体は ∪ (もしくは ∩)でプリズム。0 = φ , ∞ = X .
距離空間 M の有界な部分空間全体に M を加えたものは ∩ でプリズム。0 = M , ∞ = φ .
また、距離空間 M の非有界な部分空間全体に φ と M を加えたものは ∪ でプリズム。0 = φ , ∞ = M .
例 Γ(G) = {γ| γ は G のサイクロイド} は加法 + を ∪ としてプリズム。
双対的に、 Γ*(G) = {γ| γ は G のコサイクロイド} も加法 + を ∪ としてプリズム。
例 集合空間 ∑ に対して Π(∑) = { ∪X | X ⊂ ∑ } は ∪ でプリズム。
Γ(G) = Π(Z(G)) , Γ*(G) = Π(Z*(G))
プリズム Γ(G) を G の サイクロイドプリズム , プリズム Γ*(G) を G の コサイクロイドプリズム とよぶ。
[ 命題 6.1 ] プリズム Π の部分集合 A に対して、∩γ∈A [γ, ∞] = [Σγ∈A γ, ∞] .
プリズム Π に対してその素イデアル全体 Π# は ∪ を加法としてプリズムとなり Π の 双対プリズム(dual prism)とよぶ。
次の補題が示すように、プリズムの素イデアルは簡単なカタチをしている。
[ 補題 ] 写像 f:Π# → { [0, γ] | γ∈Π } = ( { [0, γ] | γ∈Π } , ∩ ) ,
f(p) = Π - p , は well defined で同型である。
[ 定理 6.1 ] かってなプリズム Π に対して、Π## と Π は自然に同型である。(双対定理)
<証明> 写像 Φ:Π → Π## を
Φ(γ) = Π# - [φ,Π - [0, γ]]
として定義できる。
この Φ は同型写像である。 //
最小元 0 をもつポセット P に対して 0 の直後の元を アトム( 原子, atom )とよび、その全体を Atom P で表す。
[ 命題 6.2 ] Atom ∑ = Atom Π(∑)
[ 定理 6.2 ] 集合空間 ∑ に対して、
(1) x ∈ ∪∑ ならば p(x) = {γ∈Π(∑)| x ∈ γ } は Π(∑) の原子的素イデアルである。
(2) 逆に、Π(∑) のかってな原子的素イデアル p に対して、∪∑ の要素 x が存在して p = p(x) となる。
<証明> (1)p(x) が素イデアルなことはすぐわかる。
よって x は ∑ の台に属するので p(x) は空集合φを要素として持たない空でない素イデアルということになる。
p(x) が原子的素イデアルでないとすると、φ と p(x) の間の素イデアル q がとれることになる。
p(x) の極小元全体の集合を { γ1, γ2, . . . , γn } とする。
γi(1≦i≦n)が ∑のアトム(よってΠ(∑)のアトム)でないとすると γi≠φであることからも γi は2つ以上のアトム C1, C2, . . . , Cm の合併となるが、かってな j (1≦j≦m)で Cj は γi の真部分集合で p(x) に属さないので p(x) が素イデアルということと矛盾する。
よって各 γi(1≦i≦n)は ∑のアトムである。
また p(x) = [γ1, ∞] ∪ [γ2, ∞] ∪ . . . ∪ [γn, ∞] である。
q ⊃ { γ1, γ2, . . . , γn } とすると、q がイデアルであることから
q ⊃ [γ1, ∞] ∪ [γ2, ∞] ∪ . . . ∪ [γn, ∞] = p(x) となり不合理。
よって q は { γ1, γ2, . . . , γn } を含まない。
また、q のひとつの極小元を考えると、先と同様の論法によって、それはアトムであることがわかり、p(x) の極小元でもあることになるので、
q ∩ { γ1, γ2, . . . , γn } ≠ φ である。
よって、∃i( 1≦i≦n ), γi ∈ p(x) - q
∃j( 1≦j≦n ), γj ∈ q
γi も γj も ∑のアトムゆえ γiΔγj ∈ ∑ ⊂ Π(∑).
また γi も γj も p(x) の要素なので γi Δ γj は p(x) に属さない。よって q にも属さない。
q がイデアルで γj ∈ q であることから γi ∪ γj ∈ q.
一方、γi ∪ γj = γi ∪ (γiΔγj) で γi も γiΔγj も素イデアル q に属さないことから γi ∪ γj は q に属さない。これは矛盾。
(2) ∪∑ = { x1, x2, . . . , xn },
∀i( 1≦i≦n ), p ≠ p(xi) , とする。
(1)より各 p(xi) は原子的素イデアルであるから、p と p(xi) は排他的( = お互いに包含関係がない )であり、各 i に対して p(xi) - p の要素 γi がえらべる。
p が素イデアルであることから
γ1 ∪ γ2 ∪ . . . ∪ γn は p に属さない (*)
また、各 i に対して γi ∈ p(xi) で p(xi) はイデアルであることから
γ1 ∪ γ2 ∪ . . . ∪ γn ∈ p(xi)
∴ γ1 ∪ γ2 ∪ . . . ∪ γn ∈ p(x1) ∩ p(x2) ∩ . . . ∩ p(xn) = { ∪∑ }
∴ γ1 ∪ γ2 ∪ . . . ∪ γn = ∪∑ (**)
p は空でないイデアルであるから(*)と(**)は両立しえない。 //
[ 系 ] グラフ G の辺 x が非ブリッジであれば p(x) は Γ(G) の原子的素イデアルである。
逆に、Γ(G) のかってな原子的素イデアル p に対して、あるブリッジでない辺 x が存在して p = p(x) となる。双対も成り立つ。
この系から、プリズム Π の原子的素イデアルを Πの 辺 とよぶことにする。
Πの辺全体の集合を E(Π) と書き Πの 辺集合 とよぶ。
[ 命題 6.3 ] Π をプリズム、S1, S2 ⊂ E(Π) とするとき、S1 ≠ S2 ⇒ ∩ S1 ≠ ∩ S2 .
γ∈ e ∈ E(Π) のとき e は γの 辺 とよび、その全体を γの 辺集合 とよび E(γ) で表す。
[ 命題 6.4 ] Πの部分集合 S に対して、 E(Σγ∈S γ) = ∪γ∈S E(γ).
∀γ∈Π,∩E(γ) = [γ, ∞] となっているプリズムを pregraphical とよぶ。
[ 命題 6.5 ] pregraphical なプリズム Π の要素 γ に対して,E(γ) = φ ⇔ γ = 0.
<証明> ⇒; ∩E(γ) = [γ, ∞] ,∩φ = Π = [0, ∞].
E(γ) = φ ゆえ ∩E(γ) = ∩φ ∴ [γ, ∞] = [0, ∞] ∴ γ = 0.
逆; 辺 e に対して γ∈e とすると 0∈e となり
e がイデアルであることから e ⊃ [0, ∞] = Π.これは不合理。 //
[ 命題 6.6 ] γ1,γ2 が pregraphical なプリズム Π の要素であるとき、
E(γ1) ⊃ E(γ2) ⇔ γ1≧γ2.
<証明> E(γ1) ⊃ E(γ2) ⇒ ∩E(γ1) ⊂ ∩E(γ2)
⇒ [γ1, ∞] ⊂ [γ2, ∞] ⇒ γ1≧γ2.
逆; γ1≧γ2 とする。
e ∈ E(γ2) ⇒ γ2 ∈ e ⇒ γ1 ∈ e ⇒ e ∈ E(γ1). //
[ 系 ] pregraphical なプリズム Π において、
(1) E(γ1) = E(γ2) ⇔ γ1 = γ2
(2) γ1 + γ2 = ∞ ⇔ E(γ1) ∪ E(γ2) = E(Π).
(3) (Π,+) ~ ( { E(γ) | γ∈Π } ,∪ )
[ 定理 6.3 ] pregraphical なプリズム Π において、
(1) ∩E(Π) = {∞} ,∪E(Π) = Π - {0}.
(2) Π のどんな素イデアル p もいくつかの辺の合併である。
<証明> (1) 第1式; ∩E(Π) = ∩E(∞) = [∞, ∞] = {∞}
第2式; 0 = ∞ のとき; E(Π) = φ ∴ ∪E(Π) = ∪φ = φ = Π - {0}.
0 ≠ ∞ のとき; 0 ≠ γ ∈ Π とする。
E(γ) = φ とすると ∩E(γ) = ∩φ = Π で ∩E(γ) = [γ,∞] に矛盾する。
よって γ を要素とする辺がある。 ∴ ∪E(Π) = Π - {0}.
(2) 0 = ∞ のとき; p = φ = ∪φ.
0 ≠ ∞ のとき; p = φ; p = ∪φ であるからよい。
p ≠ φ; A = ∪{ q ∈ E(Π) | q ⊂ p} とおく。
A ⊂ p である。 A ≠ p として矛盾を導けばよい。
q - A の要素 γ をとる。
ある E(γ) の要素 a があって a ⊂ p とすると γ ∈ p - A に反するから、かってな E(γ) の要素 a に対して a は p に含まれない。
E(γ) = { a1, a2, . . . , an } とする。
γi ∈ ai - p ( 1≦i≦n ) であるような γi をえらべる。
∀i ,γi ∈ Π - p ゆえ Σγi ∈ Π - p.
一方、∀i ,γi ∈ ai ゆえ Σγi ∈ ∩ai = ∩E(γ) = [γ,∞].
p は γ を要素とするイデアルなので p ⊃ [γ,∞].
∴ Σγi ∈ p. これは矛盾。 //
どんな γ ∈ Π も γ以下のアトムの和となっているプリズムを atomic(原子的)とよぶ。
実は、pregraphical と atomic は双対プリズムで対応している。
[ 命題 6.7 ]
(1) Π が pregraphical ⇔ Π# が atomic
(2) Π が atomic ⇔ Π# が pregraphical
Π も Π# も pregraphical なプリズムを graphical もしくは biatomic(双原子的)とよぶ。
あるグラフ G が存在して Π ~ Γ(G) となるようなプリズム Π を graphic ,
あるグラフ G が存在して Π ~ Γ*(G) となるようなプリズム Π を cographic , とよぶ。
また、ある集合空間 ∑ が存在して Π ~ Π(∑) となるようなプリズム Π を binary(バイナリー)とよぶ。
[ 命題 6.8 ] プリズム Π が binary ならば biatomic である。
グラフ G のフィギュア A に対して A に 付随する素イデアル p*(A) を、
p*(A) = { γ∈Γ*(G) | A ∩ γ ≠ φ }
で定義する。
[ 定理 6.4 ] A が cyclizer で p*(A) = p*(B) ⇒ B も cyclizer.
Γ*(G) においても定理 6.3(2)から素イデアルはフィギュアに付随するので、このことから
”フィギュアそのものより素イデアルを考えたほうが効率が良い”
ということになる。
プリズムは正則性と関連している。グラフの比較や分類に使うのもおもしろい。
この章では、グラフとしてはループをもたないグラフ(つまり 2 一様)のみを考える。
G の辺の集合 M でどの2要素も非隣接なのを G の 独立辺集合 もしくは マッチング(matching)という。M の要素の両端点は M で マッチされている とよばれる。
とくに G のどの頂点も M のいずれかの要素の端点となっていれば 完全マッチング とよばれる。
辺の集合 M が完全マッチングであることは言い換えると <M> が 1 因子ということである。
また、完全マッチングは辺の集合による頂点集合 V(G) の分割に他ならず、この観点からは、マッチングは部分的な分割と言える。
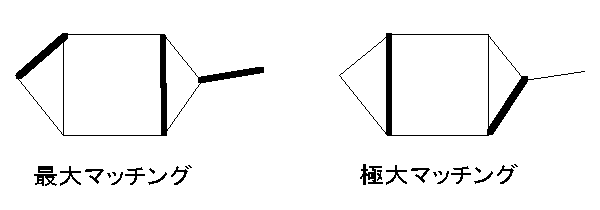
|M~|>|M| となるマッチング M~ がないとき、M は 最大マッチング 、 包含関係で極大なマッチングは 極大マッチング 、 とよばれる。マッチング理論では、分割という観点からも、最大マッチングのほうが重要である。
グラフ G の辺の集合 A に対して A と Ac の要素を交互に含むパスを A 交互道(A-alternating path)とよぶ。
とくにマッチング M に対する M 交互道の両端点が M と接合していないとき、このパスを M 増大道(M-augmenting path)とよぶ。
[ 定理 7.1 ] G のマッチング M について次は同値である。( Berge )
(1) M は G の最大マッチング.
(2) G は M 増大道をもたない.
<証明> (1)⇒(2); G のマッチング M に対して G が M 増大道 π をもつとする。
M Δ π は G のマッチングで |M Δ π| = |M| + 1 となり M は最大でないことになる。
(2)⇒(1): マッチング M は最大でないとする。
M' を最大マッチングとする。
H を <M Δ M'> とすると、 H の各点の次数は 1 か 2 である。
よって、H の各連結成分は M と M' の辺を交互にとるサイズが even のサーキットか M と M' の辺が交互にあるパスである。
|M'| > |M| なので、H のパス π で始点も終点も M に接合しないで M' に接合しているのがある。
この π は G の M 増大道である。 //
G の頂点の集合 S に対して NG (S) = { v ∈ V(G) | ∃w∈S, v adj w } を G における S の 近傍(neighbourhood)とよぶ。
[ 定理 7.2 ] G が部集合 X, Y の2部グラフのとき次は同値である。( Hall の定理 )( Hall 1935 )
(1) X のすべての要素に接合するマッチングが存在する.
(2) ∀ S ⊂ X , |N(S)| ≧ |S|.
<証明> (1)⇒(2); 明らか。
(2)⇒(1); |N(S)| ≧ |S| (∀ S ⊂ X ) とする。G が X のすべての要素に接合するマッチングを持たないと仮定して矛盾を導けばよい。
M* を G の最大マッチングとする。仮定より X に属する u で M* に接合しないのがある。
Z = { v ∈ V | v は M* 交互道により u と結ばれる } とする。
M* は最大マッチングなので定理 7.1 より u は Z の中で唯一の M* に接合しない要素である。
S = Z∩X ,T = Z∩Y とおく。
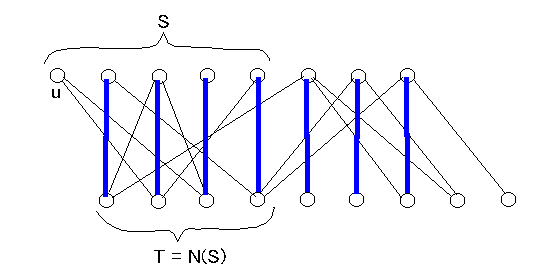
S - {u} の要素は M* により T の要素とマッチしているから |T| = |S| - 1.
また N(S) ⊃ T である。
逆に、N(S) のどの要素も M* 交互道によって u と結ばれるので N(S) ⊂ T.
∴ N(S) = T. ∴ |N(S)| = |S| - 1 < |S|. これは仮定に反する。 //
[ 系 ] k 正則な2部グラフ( k≧1 )は完全マッチングをもつ。( 結婚定理 )
(∵) G を部集合が X と Y であるような k 正則2部グラフとする。
k|X| = |E(G)| = k|Y| で k>0 より |X| = |Y| である。
S ⊂ X とし、S および N(S) に接合する辺の集合をそれぞれ E1, E2 とする。
E1 ⊂ E2 なので k|N(S)| = |E2| ≧ |E1| = k|S|.
∴ |N(S)| ≧ |S|.
よって定理 7.2 より X のすべての要素に接合するマッチングが存在する。
|X| = |Y| だからそれは完全である。 //
[ 系の系 ] k 正則な2部グラフ( k≧1 )の辺集合は k 個の完全マッチングの素和である。
[ 系 ] 2k 正則( k≧1 )なグラフ G は 2 因子を持つ。( Petersen 1891 )
<証明> 命題 2.6 より、G はいくつかのサーキットの素和である。
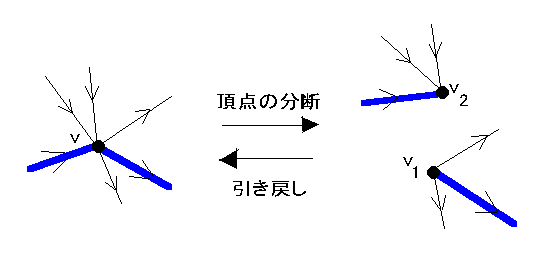
まずこれらのサーキットに一周する向きを与え、次に各頂点 v を2つの頂点 v1, v2 に分けて、各有向辺 uv を有向辺 u1v2 に置き換える。
こうしてできた2部グラフ G' は k 正則なので、上記の系より 1 因子を持ち、これを G に引き戻すと G の 2 因子となる。
//
[ 系の系 ] 2k 正則( k≧1 )なグラフの辺集合は k 個の 2 因子の素和である。
K ⊂ V(G) について、G のどの辺も K に接合するとき K は G の 点被覆 という。
サイズが最小の点被覆を 最小点被覆 とよぶ。
G の点被覆 K とマッチング M に対して、|M| ≦ |K| である。
[ 補題 ] マッチング M と点被覆 K に対して|M| = |K| であれば M は最大マッチングで K は最小点被覆.
<証明> N を最大マッチング、L を最小点被覆とすると、|M| ≦ |N| ≦ |L| ≦ |K|.
よって、|M| = |K| より |M| = |N| かつ |K| = |L|. //
[ 定理 7.3 ] 2部グラフにおいては、最大マッチングのサイズと最小点被覆のサイズは等しい。( König の定理 1931 )
<証明> G は部集合として X と Y をもつ2部グラフ、M* は G の最大マッチングとする。
X の要素で M* に接合しないのの全体を U ,U のどれかの頂点に M* 交互道で結ばれる頂点の全体を Z とする。
S = Z ∩ X ,T = Z ∩ Y とおく。
T のどの頂点も M* に接合してなくて N(S) = T である。
K~ = (X - S) ∪ T とおく。
G のどの辺も少なくとも一方の端点は K~ に属する。(∵ そうでないと S と Y - T を結ぶ辺があることになり N(S) = T に反する。)
よって K~ は G の点被覆で |M*| = |K~| である。
したがって補題より K~ は最小点被覆である。 //
9章でこの定理の別証明を述べる。
グラフの連結成分を頂点の数の偶奇によって 偶成分 と 奇成分 とに分類する。
G の奇成分の数を o(G) で表す。
次の美しい定理が成り立つ。(グラフは [s, t] ハイパーグラフの s=1, t=2 の特殊なケースであることが大きく効いてる。この定理のハイパーグラフへの拡張がなされれば大きいと思う.)
[ 定理 7.4 ] グラフ G について次は同値。( Tutte の 1 因子定理 1947 )
(1) G は完全マッチングをもつ.
(2) ∀S ⊂ V(G) ,o(G - S) ≦ |S|.
<証明> ( by Lovasz )
(1)⇒(2);
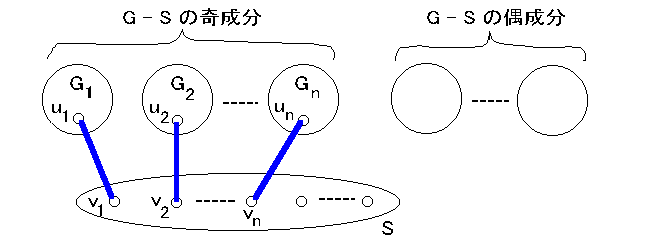
図のように、各奇成分から1本ずつ S と接合するのが出ているから。
(2)⇒(1); o(G - S) ≦ |S| ( ∀S ⊂ V(G) )で G は完全マッチングをもたないとする。
S = φ として o(G) = 0 . よって G の点の数 p は even である。
G に辺を付加していって完全マッチングをもたない極大なグラフを G~ とする。
G - S は G~ - S の全域部分グラフなので o(G~ - S) ≦ o(G - S)
∴ o(G~ - S) ≦ |S| (*)
今 U を G~ における次数が p - 1 の点の集合とする。
G~ - U の連結成分は完全グラフである。
( ∵ もし G~ - U のある連結成分が完全でないと、この成分は3点以上からなり、
xy ∈ E(G~),yz ∈ E(G~),xz は E(G~) に属さない、というような3点 x, y, z がある。
y が U に属さないことから yw が E(G) に属さないような点 w があり、w は U に属さない。
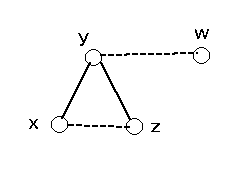
M1, M2 を G~ + xz と G~ + yw の完全マッチングとし、H を M1 Δ M2 で誘導される G~ + {xz, yw} の辺誘導部分グラフとする。
H の各点の次数は 2 ゆえ H は互いに接合しないサーキットの合併で、また、 M1 と M2 の要素は H の各サーキットで交互に接合しているから、H の各サーキットのサイズは even である。
Case 1: xz と yw が H の異なる成分に属するとき( 図(a)); yw が H のサーキット C に含まれるとする。 C の M1 の要素と C に属さない M2 の要素を合わせると G~ の完全マッチングとなり矛盾。
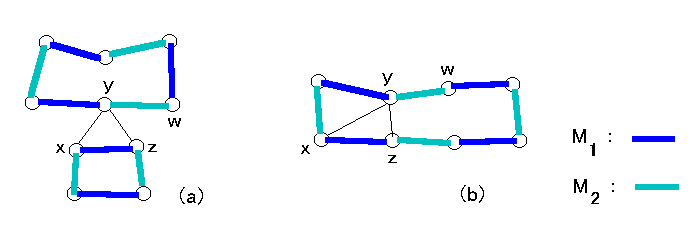
Case 2: xz と yw が H の同じ成分に属するとき( 図(b)); 点 x と点 z の対称性より、4点 x, y, z, w はサーキット C に対してこの順に並んでるものと仮定してよい。
このとき、M1 の辺で C の yw ... z の部分に含まれる辺と辺 yz および C の yw ... z の部分に含まれない M2 の辺を合わせると G~ の完全マッチングとなり矛盾。)
(*)より o(G~ - U) ≦ |U| である。 o(G~ - U) = n とする。
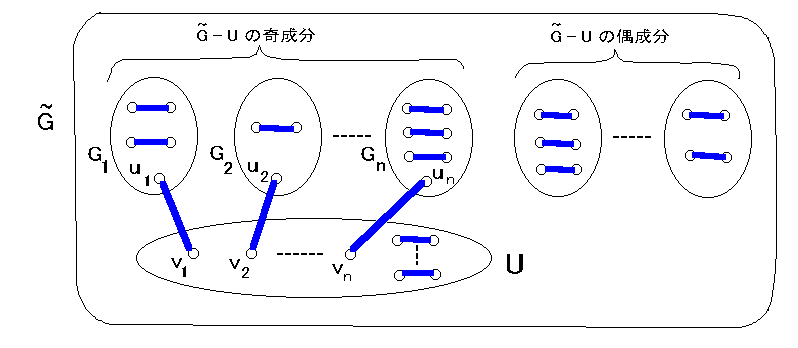
U におけるn点 v1, v2, . . . , vn をえらび Gi の点 ui をえらぶ。
図のように G~ は完全マッチングをもつ。
これは矛盾ゆえ、よって G は完全マッチングをもつ。 //
[ 系 ] グラフ G のマッチングに接合する頂点の最大数は
minS⊂V(G) { ν(G) - (o(G - S) - |S|) } である。( Tutte-Berge の公式 )
[ 系 ] ブリッジをもたない 3 正則グラフは完全マッチングをもつ。( Petersen 1891 )
(∵) G をブリッジをもたない 3 正則グラフとする。
S ⊂ V(G) , G - S の奇成分を G1, G2, . . . , Gn の n 個とし、1 ≦ i ≦ n の i について Gi と S を結ぶ辺の数を mi する。
Σv∈V(Gi) d(v) = 3|V(Gi)| かつ Σv∈S d(v) = 3|S| で
第一式より、mi = Σv∈V(Gi) d(v) - 2|E(Gi)| は odd .
G はブリッジをもたないから、mi ≧ 3 .
∴ o(G - S) = n ≦ (1/3) Σi=1n mi ≦ (1/3) Σv∈S d(v) = |S|.
よって、Tutte の定理より G は完全マッチングをもつ。 //
この Petersen の定理はほとんどそのままの証明で次のように拡張される。
[ 系 ] 2k 辺連結な 2k+1 正則グラフは完全マッチングをもつ。
G の頂点の集合 S でどの2要素も非隣接なのを G の 独立点集合 もしくは単に 独立集合 という。
サイズが最大の独立集合を 最大独立集合 ,包含関係で極大な独立集合を 極大独立集合 とよぶ。
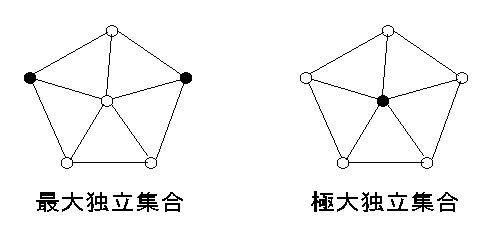
[ 命題 7.1 ] S は独立 ⇔ Sc は点被覆.
<証明> S は独立 ⇔ G のどの辺も両端点が S に属することはない
⇔ どの辺もひとつの端点は Sc に属する
⇔ Sc は点被覆 //
G の最大独立集合のサイズを G の 点独立数 もしくは 独立数 とよび α(G),
G の最小点被覆のサイズを G の 点被覆数 とよび β(G),で表示する。
[ 定理 7.5 ] α(G) + β(G) = |V(G)|.
<証明> S を G の最大独立集合,K を G の最小点被覆とする。
V - K は独立集合,V - S は点被覆だから、
|V(G)| - β = |V - K| ≦ α かつ |V(G)| - α = |V - S| ≧ β.
∴ α + β ≦ |V(G)| ≦ α + β ∴ α(G) + β(G) = |V(G)|. //
L ⊂ E(G) について、G のどの頂点も L に接合するとき L は G の 辺被覆 という。サイズが最小の辺被覆を 最小辺被覆 とよぶ。
G が辺被覆をもつ ⇔ δ(G)>0 ,である。
G の最大マッチングのサイズを G の 辺独立数 とよび α'(G),
G の最小辺被覆のサイズを G の 辺被覆数 とよび β'(G),で表示する。
[ 定理 7.6 ] δ(G)>0 のとき、α'(G) + β'(G) = |V(G)|. ( Gallai )
<証明> M を G の最大マッチング,U を M に接合しない頂点全体とする。
δ>0 なので U の各要素と接合する |U| 個の辺の集合 E' がとれる。
M ∪ E' は辺被覆だから、
β' ≦ |M ∪ E'| = α' + (|V(G)| - 2α') = |V(G)| - α'
∴ α' + β' ≦ |V(G)|.
次に、G の最小辺被覆 L をとり M を <L> の最大マッチングとする。
また、<L> の頂点で M に接合してないのの全体を U とする。
M は最大なので H[U] は辺をもたない。よって、L が辺被覆なので、
|L| - |M| = |L - M| ≧ |U| = |V(G)| - 2|M| ∴ |M| + |L| ≧ |V(G)|.
M は G のマッチングにもなってるので、
α' + β' ≧ |M| + |L| ≧ |V(G)| ∴ α' + β' ≧ |V(G)|.
よって α'(G) + β'(G) = |V(G)|. //
次の定理は König の定理( 定理 7.3 )の類似である。
[ 定理 7.7 ] δ(G)>0 の2部グラフでは独立数 α と辺被覆数 β' とは等しい。
<証明> α + β = |V(G)| = α' + β'
また、König の定理より、α' = β. ∴ α = β'. //
[ 演習問題 ] ( → 解答 )
1. 2つの完全マッチング M, M' に対して、<M ∪ M'> の成分は K2 か長さが偶数のサーキットであることを示せ。
2. 2人のプレーヤーが交互に連結グラフ G の異なる頂点 v1, v2, . . . を隣接しているように選んで行く。最後に頂点を選べたほうが勝ちとするとき、次は同値であることを示せ。
(1) 最初のプレーヤーが必ず勝てる.
(2) G は完全マッチングをもたない.
3. どんな最大次数が1以上の2部グラフもすべての最大次数の頂点と接合するマッチングをもつことを示せ。
4. 図のグラフは完全マッチングをもたないことを示せ。
5. 木は完全マッチングを高々ひとつしかもたないことを示せ。
6. T を木、v をひとつの端点とすると、T は v に接合する最大マッチングをもつことを示せ。
7. 木 G について次が成り立つことを示せ。
G は完全マッチングをもつ ⇔ ∀v ∈ V(G), o(G - v) = 1. ( Chungphaisan )
8. Tutte-Berge の公式を証明せよ。
9. 2部グラフ G(X, Y) の最大マッチングのサイズは |X| - maxS⊂X ( |S| - |N(S)| ) であることを証明せよ。
10. 定理 7.2(Hallの定理)を定理 7.3(König の定理)から導け。
11. 最大マッチング M* と極大マッチング M に対して |M|≧ |M*| / 2 であることを示せ。
12. 図の図形はドミノ(1×2 のタイル)では敷き詰めできないことを示せ。
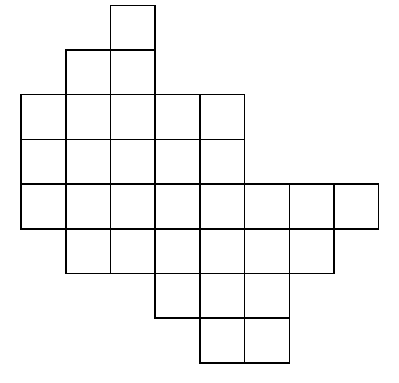
有向グラフ(directed graph, digraph) D とは3つ組 (V(D), A(D), ψD) のことである。
但し V(D)∩A(D)=φ, ψD: A(D) → V(D)×V(D) とする。 A(D) の代わりに E(D) とかくこともある。
A(D) の要素を 弧(arc)または 有向辺(directed edge) とよぶ。
有向グラフ D の弧を非順序対に変えて得られるグラフ G を D の 基礎グラフ(underlying graph)という。
逆に、グラフ G に対して各辺を順序対に変えて得られる有向グラフ D を G の 向きづけ(によって得られた有向グラフ)という。
グラフについての用語は適宜有向グラフに対しても使用する。
ψD(a) = (u, v) のとき a = (u, v) もしくは a = uv とかき、弧 a は点 u を点 v に 結ぶ といい, u を a の 始点 , v を a の 終点 とよぶ。
有向グラフを図示するとき、弧は矢をつけた単純曲線で表す。
D の点 v に対し、
O(v) = { a ∈ A(D) | a は v を始点とする } , I(v) = { a ∈ A(D) | a は v を終点とする }
とする。
|I(v)| を dD-(v) ( または単に d-(v) )で表し v の 入次数(in-degree)または 入り次数 , |O(v)| を dD+(v) ( または単に d+(v) )で表し v の 出次数(out-degree), とよぶ。
[ 命題 8.1 ] 有向グラフ D において, Σv∈V(D) d-(v) = Σv∈V(D) d+(v) = |A(D)|.
特定の2点 s, t をもつ有向グラフ D と 重み付け関数 c: A(D) → R≧0 ∪ {∞} とからなるシステム N = (D, s, t, c) を ネットワーク(network)と呼ぶ。( R≧0 は非負の実数全体の集合 )
D は N の 基礎有向グラフ とよばれる。
s を ソース(source, 入り口 )、t を シンク(sink, 出口 )、ソースでもシンクでもない点を 内点(inner vertex)、とよぶ。
c を 容量関数(capacity function), 弧 a に付けられた重み c(a) を a の 容量 , とよぶ。
関数 f: A(D) → R≧0 が次の条件を満たすとき f を N の フロー(flow, 流れ )と呼ぶ。
(ⅰ) 任意の弧 a に対して、f(a) ≦ c(a).( 制限条件 )
(ⅱ) 任意の内点 v に対して、Σa∈O(v) f(a) = Σa∈I(v) f(a).( 保存条件 )
すべての弧 a に対して f(a) = 0 である f はフローで 零フロー とよばれる。
記法の便宜上 X , Y ⊂ V に対して ∑a = xy , x∈X, y∈Y f (a) を f (X, Y) と書くことにする。
また、S ⊂ V に対して f + (S) = f (S, Sc), f -(S) = f (Sc, S) とする。
D の各点 v に対して、f + ({v}) を f + (v) , f - ({v}) を f - (v) と略記する。
保存条件(ⅱ)は任意の内点 v に対して,f + (v) = f - (v) と書き替えできることになる。
[ 定理 8.1 ] ネットワーク N = (D, s, t, c) の任意のフロー f に対して、
f + (s) - f - (s) = f - (t) - f + (t).
<証明> 各弧はその始点と終点で1回ずつ f + と f - の中で使われるから、
Σv∈V(D) f + (v) = Σv∈V(D) f - (v).
左辺と右辺はそれぞれ
Σv∈V(D) f + (v) = f + (s) + f + (t) + Σv∈V(D)-{s,t} f + (v).
Σv∈V(D) f - (v) = f - (s) + f - (t) + Σv∈V(D)-{s,t} f - (v).
また、保存条件より内点 v に対して f + (v) = f - (v).
∴ f + (s) + f + (t) = f - (s) + f - (t). //
定理の式で与えられる値をフロー f の 値(value)といい val(f) で表す。
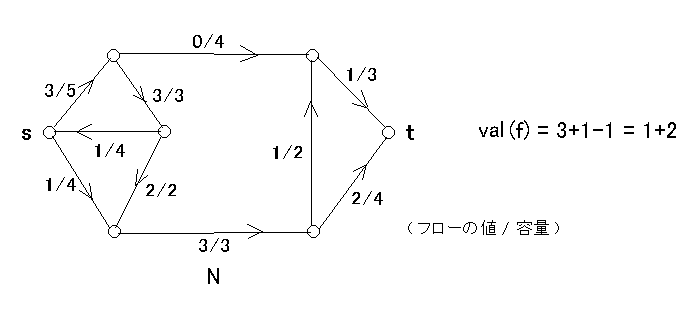
ネットワーク N のフローで値が最大となるのを 最大フロー(max flow, 最大流 )とよぶ。
ネットワーク N = (D, s, t, c) において、s ∈ S, t ∈ Sc ( = V(D) - S ) である点の集合 S ⊂ V(D) に対して、S の点を始点とし Sc の点を終点とする弧全体の集合を (S, Sc)、Sc の点を始点とし S の点を終点とする弧全体の集合を (Sc, S) で表す。(S, Sc) を S で決まる N の カット と呼ぶ。弧の集合はある点の集合 S で決まるカットのとき カット とよぶ。
カット K に属する弧の容量の総和を K の 容量 といい cap(K) で表す。
[ 定理 8.2 ] ネットワーク N = (D, s, t, c) のフロー f とカット K = (S, Sc) に対して
val (f) = f + (S) - f - (S) = f - (T) - f + (T) ( ただし T = Sc. )
<証明> val (f) = ∑v∈S (f + (v) - f - (v))
= ∑v∈S f + (v) - ∑v∈S f - (v)
= ( f(S, S) + f(S, T) ) - ( f(S, S) + f(T, S) )
= f(S, T) - f(T, S)
= f + (S) - f - (S)
= f - (T) - f + (T) //
[ 定理 8.3 ] 任意の流れ f と任意のカット K に対してval(f) ≦ cap(K).
<証明> K = (S, Sc) とする。( S ⊂ V(D) )
任意の弧 a に対して f(a) ≦ c(a) であるから、f + (S) ≦ cap(K).
一方任意の弧 a に対して 0 ≦ f(a) であるから、f - (S) ≧ 0.
∴ f + (S) - f - (S) ≦ cap(K).
よって定理 8.2 より val(f) ≦ cap(K). //
ネットワーク N のすべてのカットのうちで最小の容量を持つカットを N の 最小カット と呼ぶ。
定理 8.3 より N のどのフローの値も最小カットの容量を越えないから次を得る。
[ 系 ] フロー f とカット K について val(f) = cap(K) が成り立てば f は最大フローで K は最小カットである。
ネットワーク N のパス P に含まれる各弧 a に対して a の P に対する 非飽和度 τ(a) を、
弧 a が P と同じ向きのとき c(a) - f(a)
弧 a が P と反対向きのとき f(a)
と定義し、τ(P) = min {τ(a) | a は P に含まれる弧 } とする。
定義より τ(P) ≧ 0 であるが、特に τ(P) = 0 のとき P は f に対して 飽和
している(saturated)とよぶ。
また N のソース s をシンク t に結ぶ f に対して飽和していないパスを N の f に対する 増大パス(augmenting path)とよぶ。
もし N に f に対する増大パス P があれば f を修正したフロー f~ を次のように構成する。
P 内の弧 a が P と同じ向きのとき、f~(a) = f(a) + τ(P).
P 内の弧 a が P と反対向きのとき、f~(a) = f(a) - τ(P).
弧 a が P に属さないとき、f~(a) = f(a).
このとき、val(f~) = val(f) + τ(P) > val(f) となる。
よって N の最大フロー f に対する増大パスは存在しない。
[ 定理 8.4 ] ネットワーク N のフロー f が N の最大フロー ⇔ N には f に対する増大パスは存在しない.
<証明> ⇒ は示してあるので逆のほうを示す。
ソース s から f に対して飽和していないパスを使って到達可能な点の集合を S とする。
s ∈ S であり、また N が f に対する増大パスを含まないことから t ∈ Sc となるので K = (S, Sc) は N のカットになる。
S の定義よりカット K に属する任意の弧 a に対し c(a) = f(a) が成り立つ。(∵ そうでないとするとカット K に属す弧 a = (u, v) に対し u に至る f に対して飽和していないパスに a を加えると v にも到達できてしまって v ∈ Sc に反する。)また、K' = (Sc, S) に属す任意の弧 a に対し f(a) = 0 が成り立つ。
∴ cap(K) = f + (S) - f - (S).
また、定理 8.2 より、
f + (S) - f - (S) = val(f).
さらに、fmax を N の最大フロー、Kminを N の最小カットとすると、定理 8.3 より、
val(f) ≦ val(fmax) ≦ cap(Kmin) ≦ cap(K)
以上より、val(f) = val(fmax). //
例
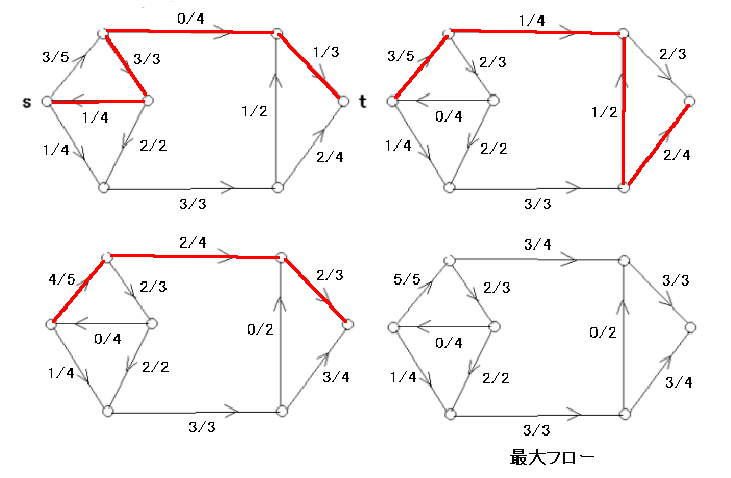
定理 8.4 の証明より次の有名な定理をえる。
[ 定理 8.5 ] (最大フロー・最小カットの定理)
任意のネットワーク N に対して、最大フローの値と最小カットの容量は等しい。( Ford and Fulkerson 1956 )
各弧の値が整数であるフローを 整数フロー( integral flow )とよぶ。
[ 定理 8.6 ] 各弧の容量が整数であれば整数最大フローが存在する。
<証明> 零フローから始めて修正フローを作って行けば良い。 //
[ 演習問題 ] ( → 解答 )
1. Hall の定理を最大フロー・最小カットの定理を使って示せ。
グラフはいくつかの点をいくつかの線でつないだモノであるから連結性の考察は基本的なテーマと言える。
グラフ G の点の集合 S が ξ(G - S) > ξ(G) をみたすとき S を G の 分離集合(separating set)とよぶ。
ループをもたないグラフ G の頂点 v について、v は切断点 ⇔ {v} は分離集合、である。
G が連結であるとき G の分離集合のサイズの最小値を G の 点連結度(vertex connectivity)もしくは単に 連結度 とよび κ(G) で表す。
完全グラフおよび完全グラフに辺をいくつか付加したグラフは分離集合をもたないが、便宜上そのようなグラフ G の点連結度は |V(G)| - 1 と規約する。
グラフ G の辺の集合 X が ξ(G - X) > ξ(G) をみたすとき X を G の 分断集合(disconnecting set)とよぶ。
G が連結であるとき G の分断集合のサイズの最小値を G の 辺連結度(edge connectivity)とよび λ(G) で表す。
|V(G)| = 1 のグラフは分断集合をもたないが、便宜上そのようなグラフ G の辺連結度は 0 と規約する。
|V(G)| ≧ 2 の連結グラフの辺連結度はボンドのサイズの最小値に他ならない。
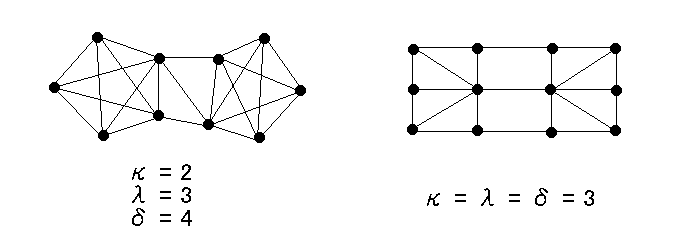
[ 命題 9.1 ] 任意の連結グラフ G に対して κ(G) ≦ λ(G) ≦ δ(G) が成り立つ。( Whitney 1932 )
<証明> |V(G)| = 1 のときは規約により κ(G) も λ(G) も 0 で、また δ(G) は 0 以上だから成立する。
|V(G)| ≧ 2 のとき; 各頂点 v に対してそのコバウンダリーカット δ(v) は分断集合であるから λ(G) ≦ |δ(v)|.また |δ(v)| ≦ deg(v). ∴ λ(G) ≦ δ(G).
よってあとは κ(G) ≦ λ(G) のみ示せばよいことになる。
平行な辺があるときそのうちのひとつを除去しても κ(G) は変化せず λ(G) は増加しないので、G は平行な辺をもたないとして示せば十分である。
λ(G) = 0 であれば κ(G) = 0 ,また λ(G) = 1 であればブリッジ b をもち K2 にループを付加したグラフであれば κ(G) = 1 そうでなければ b の端点のうちいずれかは切断点でやはり κ(G) = 1 である。
λ(G) ≧ 2 のとき; X を |X| = λ(G) であるボンドとする。
e = uv ∈ X に対して G' = G - (X - {e}) とおく。
G' は連結で e をブリッジとして持つ。
X - {e} の各要素について u, v 以外の端点を選び頂点の集合 S をつくる。
G - S が非連結であれば κ(G) ≦ |S| = λ(G) - 1 となるので κ(G) < λ(G).
G - S が連結であれば e は G - S のブリッジで G - S = <e> であるか u, v のいずれかは G - S の切断点になっていて、どちらの場合も κ(G) ≦ |S| + 1 = λ(G) となるので κ(G) ≦ λ(G). //
連結グラフ G が κ(G) ≧ n を満たすとき n 点連結(n-vertex connected)もしくは単に n 連結 ,λ(G) ≧ n を満たすとき n 辺連結(n-edge connected),とよぶ。
頂点数が3以上のブロックは 2 連結である。
グラフ G の2点 u, v が G の分離集合 S によって異なる連結成分に分けられるとき S は点 u, v を 分離する とよぶ。u と v を分離する S のサイズの最小値を u と v の間の 局所点連結度(local vertex connectivity)もしくは単に 局所連結度 とよび κ(u, v) で表す。κ(u, v : G) と明記することもある。
いくつかのパスはどの2つも端点以外の点(内点)を共有しないとき 内素 であるとよぶ。またどの2つも点を共有しないとき 点素 であるとよぶ。
[ 定理 9.1 ] グラフ G の非隣接点 a, b 間の局所点連結度 κ(a, b) は内素な ab パスの最大数に等しい。( Menger の定理 1927 )
< 証明 > κ(a, b) = k とする。
ab パスは κ(a, b) を与える a と b の分離集合の要素を必ず通るので内素な ab パスの数は k 本以下である。
よって、k 本の内素な ab パスがとれることを示せばよい。
ε(G) でのインダクション。
ε(G) = 0 のときはあきらかなので G は辺 e = xy を持つと仮定してよい。
G が k 本の内素な ab パスを持たないなら G/e も持たない。ただしここで縮約で生じた頂点 ve は G で a inc e であれば G/e で a とする。b に関しても同様とする。
帰納法の仮定により G/e は k 点未満の a と b の分離集合 Y を持つ。
Y が ve を要素としなければ Y は G における a と b の分離集合となってしまうから ve は Y に属する。
X = (Y - ve) ∪ {x, y} は k 点以下となるので丁度 k 点であることになる。
ここで G - e を考えてみる。
G - e の a を含む連結成分を1点 a* に縮約してできるグラフを Ga , b を含む連結成分を1点 b* に縮約してできるグラフを Gb とする。
x, y ∈ X なので Ga での a と b の分離集合は G での a と b の分離集合でもあり少なくとも k 点を含む。よって仮定より Ga での内素な k 本の a*b パスが存在する。
同様にして Gb での内素な k 本の ab* パスが存在する。これらを自然に結び付けることで k 本の内素な ab パスが構成される。 //
[ 系 ] グラフ G が n 連結 ⇔ 異なる2頂点に対してそれを結ぶ n 本の内素なパスが存在する。( Whitney 1932 )
A, B ⊂ V(G) と uv パス P に対して A ∩ V(P) = {u}, B ∩ V(P) = {v} であるとき P を AB パス ともよぶ。
A, B, X ⊂ V(G) に対して G におけるどの AB パスも X の要素を通るとき X は G において A と B を 分離する とよぶ。( A ∩ B ⊂ X であることに注意.)
[ 定理 9.2 ] G をグラフとし、A, B ⊂ V(G) とするとき、 G において A と B を分離する頂点の数の最小値は G における互いに点素な AB パスの本数の最大値に等しい。( Menger の定理の別形 )
<証明> 新しい2点 a, b とし G~ = a*AG*Bb とする。
この定理の主張は G~ での定理 9.1 の主張と同値である。 //
[ 系 ] 定理 7.3( König の定理 )
グラフ G の2点 u, v がボンド X によって異なる連結成分に分けられるとき X は u と v を 分断する とよぶ。 u と v を分断する X のサイズの最小値を u と v の間の 局所辺連結度(local edge connectivity)といい λ(u, v) で表す。
いくつかのパスは辺の集合として互いに素であるとき 辺素(edge disjoint)であるとよぶ。
[ 定理 9.3 ] グラフ G の2点 u, v 間の局所辺連結度 λ(u, v) は辺素な uv パスの最大数に等しい。
<証明> 定理 9.1 と同様に示すこともできるがここでは「線グラフ」を使って示すことにする。G の 線グラフ(line graph) L(G) とは V(L(G)) = E(G) で G で隣接する2辺を辺で結んだグラフである。
G はループをもたないとしてよい。
L(G) に新しい頂点 u*, v* を加え u と接合してる辺と u*, v と接合してる辺と v* を辺で結んでできるグラフを G' とする。
κ(u*, v*: G') ≧ λ(u, v) である。
よって G' において λ(u, v) 本の内素な u*v* パスが存在し、これから λ(u, v) 本の辺素な uv パスをえる。 //
[ 系 ] グラフ G が n 辺連結 ⇔ 異なる2頂点に対してそれを結ぶ n 本の辺素なパスが存在する。
[ 定理 9.4 ] |V(G)| ≧ n + 1 のグラフ G に対して次は同値。
(1) n 点連結.
(2) 任意の 2 点に対して n 本の内素な uv パスが存在する.
(3) 任意の n + 1 点 v, v1, v2, . . . , vn に対して内素な vvi パスたちが存在する.
(4) 任意の n + 1 点 u, v, w1, w2, . . . , wn-1 に対して wi( 1≦i≦n-1 )を通らない uv パスが存在する。
(5) 任意の n - 1 点に対してそれらを端点としてもつ生成木が存在する.
<証明> (1)⇒(2)⇒(3)⇒(4)⇒(5)⇒(1)で示す。
(1)⇒(2); G を n 点連結グラフ,u, v を G の2頂点とする。
u, v が隣接していなければ n ≦ κ(G) ≦ κ(u, v) であるから、メンガーの定理より u と v の間には n 本の内素なパスが存在する。
u と v が隣接している場合; u と v を結ぶ辺をすべて除去してえられるグラフ G' とする。 G が n 点連結なので G' における u, v 間の局所点連結度は n - 1 以上である。したがってメンガーの定理より G' には n - 1 本の内素な uv パスが存在し、これに u と v を結ぶ辺 e を加えると G における n 本の内素な uv パスが得られる。
(2)⇒(3); 任意の 2 点に対して n 本の内素な uv パスが存在するならあきらかに n 連結である。
新しい点 w とし G~ = w *{v1, v2, . . . , vn} G を作ると G~ も n 連結であり(1)⇒(2)を G~ に適用すると n 本の内素な vw パスが存在することがわかる。これらを G に制限すると内素な vvi パスたちを得る。
(3)⇒(4); n 本の内素な uv パス, uw1 パス, . . . , uwn-1 パスが存在するので。
(4)⇒(5); n - 1 点 v1, v2, . . . , vn-1 以外の2点 P, Q がとれる。vi(1≦i≦n-1)を通らない PQ パス π がある。
P, Q, vi(1≦i≦n-1)以外の点 R があれば vi(1≦i≦n-1)を通らない PR パスがあるので π を P, Q, R に接合し vi(1≦i≦n-1)とは接合しない木に拡大できる。
この操作を繰り返すことにより vi(1≦i≦n-1)に接合しない木 S を構成できる。
次に Pvi パスで Q, v1, . . . , vi-1, vi+1, . . . , vn-1 を通らないのがあるので S を v1, v2, . . . , vn-1 を端点とする生成木に拡大できる。
(5)⇒(1); (5)より任意の n - 1 点を除去しても連結である。
|V(G)| ≧ n + 1 ゆえ n - 1 点を除去して1点のみということはないから G は n 連結ということになる。 //
[ 定理 9.5 ] n 点連結グラフ(n≧2)のかってな n 点に対してそれらを通るサーキットが存在する。( Dirac 1960 )
<証明> X を G の n 点の集合とする。
C を X の頂点をできるだけ多く含むサーキット,|V(C) ∩ X| = m とする。
もしも m < n だと C 上にない X の頂点 v があることになる。
定理 9.4 の(1)⇒(3)より v から V(C) への min {n, |V(C)|} 本の内素なパスが存在する。
C 上の X の頂点たちは点の共有は無視して C を m 個の断片に分けているが、これらのうちの少なくとも2つのパス P, Q は C の同じ断片で終わっていることになる。
よって P の終点 p と Q の終点 q で分けられる C の2つの断片のうちどちらかは X のすべての頂点を含む。
それを C[p, q] とすると P ∪ Q ∪ C[p, q] は C よりも多く X の点を含むサーキットとなり C のえらび方に反する。 //
頂点の代わりに辺としたらどうであろうかと考えるのは自然であるが、これに関して次のような定理がある。
[ 定理 9.6 ] n 連結グラフのどのサイズ n - 1 の独立辺集合もあるサーキットに含まれる。( Haggkvist and Thomassen 1982 )
全域的なサーキットを ハミルトンサーキット , ハミルトンサーキットをもつグラフを ハミルトングラフ とよぶ。
ハミルトンサーキットの概念はそれほど重要ではないが次の定理は深い定理である。
[ 定理 9.7 ] 4 連結な平面的グラフはハミルトンサーキットをもつ。( Tutte 1956 )
全域的なパスを ハミルトンパス , 任意の異なる2点を結ぶハミルトンパスが存在するグラフを ハミルトン連結 とよぶ。
定理 9.7 は次のように拡張されている。
[ 定理 9.8 ] 4 連結な平面的グラフはハミルトン連結である。( Plummer and Thomassen 1983 )
[ 定理 9.9 ] Menger の定理から Hall の定理がみちびける。
<証明> G を X と Y を部集合とする2部グラフとする。近傍のサイズについての条件から X のすべての要素に接合するマッチングが存在することを示せればよい。
新しい頂点 u と G を X でジョインし更に別の新しい頂点 v と Y でジョインしたグラフを G~ とする。
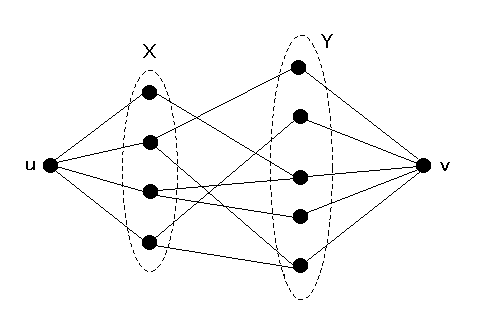
所望のマッチングが存在するための必要十分条件は内素な uv パスが |X| 本とれることである。したがって、Menger の定理により、u と v を分離する G~ の分離集合 S のサイズが |X| 以上であることを示せばよいということになる。
A = S ∩ X , B = S ∩ Y とおく。
S = A ∪ B は u と v を分離するので X - A の点と Y - B の点を結ぶ辺は存在しない。
∴ N(X - A) ⊂ B.∴ |X - A| ≦ |N(X - A)| ≦ |B|.
よって、|S| = |A| + |B| ≧ |X|. //
実は更に Menger の定理は最大フロー・最小カットの定理からみちびけることが知られている。
グラフについて調べるとき、ある程度連結の度合いが高いグラフに制限して考えても良いことが多い。
[ 演習問題 ] ( → 解答 )
1. 連結グラフ G について次は同値であることを証明せよ。
(1) 分離集合をもつ.
(2) 非隣接な2点が存在する.
2. 頂点数が2以上の連結グラフは切断点でない頂点を2個以上もつことを示せ。
3. かってな整数 1≦r≦s≦t に対して κ = r, λ = s, δ = t である単純グラフが存在することを示せ。
4. κ(Qn) = n を示せ。
5. 単純な3正則グラフ G に対しては κ(G) = λ(G) であることを示せ。
6. κ(v * G) = κ(G) + 1 を示せ。
7. 2連結グラフ G のかってな頂点 v に対して v と隣接する頂点 u で G - u - v が連結となるのが存在することを示せ。
8. 頂点数が5以上のどんな3連結グラフ G も、G/e がやはり3連結となるような辺 e をもつことを示せ。( Thomassen )
9. G の頂点の集合 S は κ(v *S G) = κ(G) + 1 をみたすとき (点連結度についての)持ち上げ集合(lifting set)とよぶことにする。
単純グラフ G については、n 連結かつ n 正則であることと持ち上げ集合は V(G) のみであることとは同値であることを示せ。
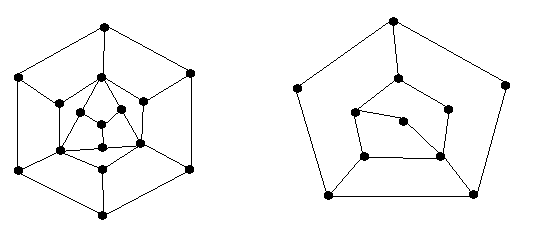
10. 図の2つの連結グラフはどちらもハミルトングラフではないことを示せ。
11. G がハミルトングラフのとき φ≠ S ⊂ V(G) なる任意の S について ξ(G - S) ≦ |S| であることを示せ。
12. 頂点数が3以上で κ(G)≧α(G) のグラフはハミルトングラフであることを示せ。( Chvatal-Erdös )
13. 奇グラフのひとつの辺を通るハミルトンサーキットの総数は even であることを示せ。( Smith-Thomason )
[ 補題 ] 連結な平面グラフ G の生成木 T に対して T* = { e*| e ∈ T } は G* の補木である。
<証明> (T*)c = E(G*) - T* が G* の生成木であることを示せばよい。
(T*)c がサーキットを含まないこと;
サーキットを含むとする。G で対応する辺の集合はコサーキットで T と交わらないことになり不合理。
(T*)c が連結であること;
(T*)c が非連結であるとする。
ひとつの連結成分を A , 残りを B とする。
U を <A> に属する G* の頂点を境界に含む面たちの合併とする。
B の頂点は U の閉包に属さないから U の境界 Bd(U) は空ではない。
Bd(U) は T のいくつかの辺からなっていて、その各辺の一方の側は U に含まれる面に接し、他方の側は U に含まれない面に接している。
よって Bd(U) には次数が 1 の頂点は属していない。
また、Bd(U) の連結成分はいくつかのリンクからなるので 1 点のみということはない。
よって Bd(U) はサーキットを含み T が木であることに反する。
以上より (T*)c は木で、G* のすべての頂点と接合しているので生成木。 //
[ 定理 10.1 ] 連結な平面グラフ G の頂点、辺、面の数を v,e,f とすると, v - e + f = 2 .(オイラーの公式 1752 )
<証明> T を G のひとつの生成木とする。
補題により (Tc)* = { e*| e ∈ Tc } は双対グラフ G* の生成木なので
(v - 1) + (f - 1) = e . ∴ v - e + f = 2 .
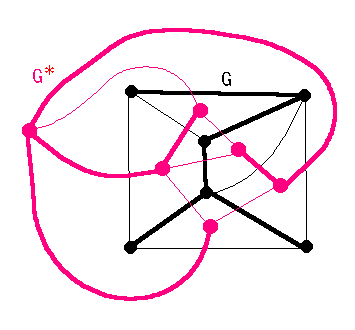
(図で 太い黒線が T ,太い赤線が (Tc)* ,v - 1 = |T|, f - 1 = |(Tc)*| .) //
<別証> T を G の生成木、e を T の枝とする。
G - e も平面グラフで生成木 T をもつから連結である。
G - e の頂点の数は G の頂点の数と等しく、辺の数も面の数も G より 1 個少ない。
よって、(頂点の数) - (辺の数) + (面の数) は G と変わらない。
枝の除去を繰り返すと最終的には <T> になるが、<T> については
v - e + f = (v - e) + f = 1 + 1 = 2 となっている。
よって、G においても v - e + f = 2 である。 //
[ 注 ] 辺の縮約でも同様に示される。すぐあとでも別の証明を述べる。(定理 10.4 の系)
[ 系 ] 連結な平面的グラフの平面的実現の面の数は埋め込みによらず一定である。
ループや多重辺を付加しても平面性に影響しないがそうでない辺を付加すると平面性が壊れる可能性がある。
次の命題は単純平面グラフの辺数はあまり多くなりえないということを表現している。
[ 系 ] |V(G)| ≧ 3 の単純平面グラフ G に対して、|E(G)| ≦ 3|V(G)| - 6.
(∵) 連結として示せば十分である。
どの面の次数も3以上なので Σ面 F d(F) ≧ 3f ∴ 2e ≧ 3f
∴ v - e + 2e/3 ≧ v - e + f = 2 ∴ 3v - 6 ≧ e. //
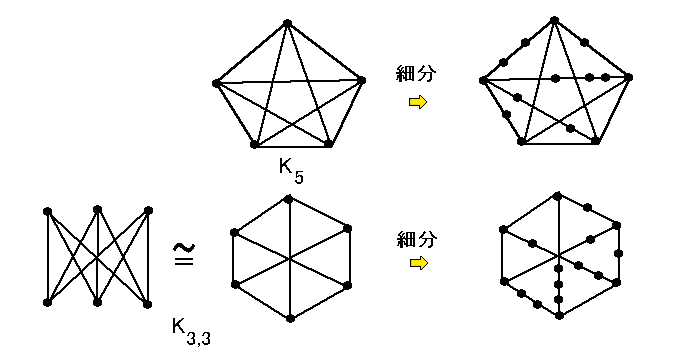
[ 系 ] K5 と K3,3 は平面的でない。
(∵) K5 が平面的とすると |E(K5)| ≦ 3|V(K5)| - 6 で 10 ≦ 9 となり不合理。
K3,3 が平面的とすると、その平面的実現 G の各面の次数は4以上であり
4f ≦ Σ面 F d(F) = 2e = 18 ∴ f ≦ 4
∴ 2 = v - e + f ≦ 6 - 9 + 4 = 1. 不合理。 //
辺 e = uv をグラフ G から除去して、新しい点 w と 2辺 uw , vw を加えるという操作を G の 初等細分 (elementary subdivision) とよび、初等細分の合成もしくは合成によって得られるグラフを 細分 という。
グラフ G の細分と グラフ H の細分が同型になるとき G と H は 同相(homeomorphic)とよぶ。
次の定理が成り立つ。証明は若干長いので14章補充にまわすことにする。
[ 定理 10.2 ] グラフ G について次は同値。( Kuratowski の定理 1930 )
(1) 平面的.
(2) K5 の細分も K3,3 の細分も部分グラフとして含まない。
[ 命題 10.1 ] ループをもたない 2 連結平面グラフの面の境界はサーキットである。
[ 定理 10.3 ] 3 連結単純平面グラフのサーキット C について次は同値。
(1) ある面 f があって C = β(f).
(2) 商グラフ G / C はブロック.
[ 定理 10.4 ] 平面グラフの有限面のバウンダリー全体はサイクル空間 Z(G) の基底である。
<証明> 各サーキットはその内部にある面のバウンダリー全体の和であるから有限面のバウンダリー全体はサイクル空間を生成する。有限面は |E(G)| - |V(G)| + ξ(G) = dim Z(G) 個あるから基底であることになる。 //
[ 系 ] 定理 10.1(オイラーの公式)
(∵) G を頂点、辺、面の数が v,e,f の連結な平面グラフとすると
f - 1 = e - v + 1
∴ v - e + f = 2 //
[ 定理 10.5 ] グラフ G について次は同値である。( MacLane 1937 )
(1) 平面的.
(2) 各辺がその高々2個の要素に属するような Z(G) の基底が存在する.
<証明> 各辺がその高々2個の要素に属するような Z(G) の基底を M 基底 とよぶことにする。
(1)⇒(2); 各辺は有限面のバウンダリー全体の高々2個の要素に属するから定理 10.4 により有限面のバウンダリー全体は M 基底である。
(2)⇒(1); ν(G) ≦ 2 のときはあきらかなので ν(G) ≧ 3 とする。
κ(G) ≦ 1 であれば G は |V(G1) ∩ V(G2)| ≦ 1 である2つの誘導真部分グラフ G1 と G2 の合併で Z(G) は Z(G1) と Z(G2) の直和であり Z(G) が M 基底をもつことと Z(G1) と Z(G2) が M 基底をもつこととは同値である。
また、G が平面的であることと G1 と G2 が平面的であることも同値である。
よって G は 2 連結として示せばよいことになる。
G は 2 連結,B = { z1, z2, . . . , zn } は Z(G) の M 基底とする。
G の辺 e に対して e が B の要素のうちのたとえば z1 のみに属しているときは { z2, . . . , zn } は Z(G - e) の M 基底である。
また e が B の要素のうちのたとえば z1 と z2 に属しているときは { z1 + z2, z3, . . . , zn } は Z(G - e) の M 基底である。
したがって G の任意の部分グラフのサイクル空間が M 基底を持つことになる。
よってあとは K5 と K3,3 が M 基底をもたないことを示せば良いということになる。(∵ そのときは K5 の細分も K3,3 の細分も M 基底をもたないので G は K5 の細分も K3,3 の細分も含まないことになり Kuratowski の定理により平面的 )
dim Z(K5) = 6 であるから B = { z1, . . . , z6 } を K5 の M 基底とする。
z0 = z1 + . . . + z6 とする。
B が1次独立であることからどの zi(0≦i≦6)も空ではなくサイズは3以上である。
∴ 18 = 6 × 3 ≦ |z1| + . . . + |z6|
≦ 2 ε(K5) - |z0|
≦ 2 × 10 - 3 = 17 矛盾。
dim Z(K3,3) = 4 であるから B = { z1, . . . , z4 } を K3,3 の M 基底とする。
z0 = z1 + . . . + z4 とする。
各 zi(0≦i≦4)のサイズは4以上である。
∴ 16 = 4 × 4 ≦ |z1| + . . . + |z4|
≦ 2 ε(K3,3) - |z0|
≦ 2 × 9 - 4 = 14 矛盾。 //
[ 定理 10.6 ] 連結グラフ G について次は同値。( Whitney 1933 )
(1) 平面的.
(2) あるグラフ G# と E(G) から E(G#) への全単射 Φ が存在して、 G の生成木 T に対して Φ(T) が G# の補木となり、またこの逆も成り立つ。(このような G# は G の 抽象的双対 グラフ とよばれる.)
<証明> (1)⇒(2); G の平面的実現をやはり G とする。
G# = G* とすれば Φ(e) = e* は(2)の条件を満たす。
(2)⇒(1); G# と Φ が(2)の条件を満たすとする。
X ⊂ E(G) について、Φ(X) が G# でのコバウンダリー δG#(v) とする。
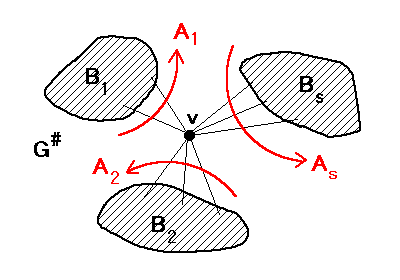
B1, B2, . . . , Bs を v についての G# の「分岐」(図の部分グラフまたは頂点の集合)とし、Ai を v と Bi を結ぶ辺全体の集合とする。
Ai は G# のすべての生成木と交わる辺の集合のうち極小なので原像 Φ-1(Ai) は G のどんな生成木にも含まれない辺の集合のうち極小で、よって Φ-1(Ai) はサーキットである。
よって X = Σi=1s Φ-1(Ai) は G のサイクルである。
ここで、C1, C2, . . . , Cν# を G# の各頂点のコバウンダリーに対応する G のサイクルとする。
G の各辺は丁度2つの Ci に含まれている。
また f = ν# - 1 とすると C1 , C2 , . . . , Cf は Z(G) の基底となる。
よって、MacLane の判定基準により、 G は平面的である。 //
[ 演習問題 ] ( → 解答 )
1. 定理 10.1 の最初の系は非連結でも成り立つか。
2. どんな単純平面グラフも次数が 5 以下の頂点を持つことを示せ。
3. 頂点数が4以上のどんな単純平面グラフも次数が 5 以下の頂点を4個以上持つことを示せ。
4. Petersen グラフ( → 1章演習問題5 )は平面的でないことを示せ。
5. グラフ G について次は同値であることを証明せよ。( Wagner )
(1) 平面的.
(2) K5 も K3,3 もマイナーとして含まない。