慡擔杮戝妛墂揱偐傜
偼偠傔偵
偙偙偱偼丄慡擔杮戝妛墂揱偲敔崻偺杮慖偺惉愌偺娭學傪専摙偟偰傒傑偡乮敔崻偺梊慖夛偲杮慖偲偺惉愌偺娭學偺専摙帪偺撪梕傪慜採偵偟偰榖傪恑傔偰偄傞偺偱丄枹撉偺曽偼乽仭梊慖夛偐傜乿偺崁傕嶲徠偄偨偩偒偨偔丅側偍柺搢側偺偱丄埲壓偦傟偧傟傪乽慡擔杮倴倱敔崻乿丄乽梊慖夛倴倱杮慖乿偲彂偒傑偡亅杮崁偱偼丄梊慖夛偼敔崻偺梊慖夛傪堄枴偟傑偡乯丅
偝偰丄乽慡擔杮倴倱敔崻乿丄乽梊慖夛倴倱杮慖乿偺偦傟偧傟偺慻傒崌傢偣偺椶帡揰丄憡堘揰傪峫偊傞偲丄埲壓偺傛偆側偙偲偑尵偊傞偲巚偄傑偡乮摉偨傝慜偺偙偲偱偡偑榖偺慻傒棫偰偲偄偆偙偲偱偛梕幫傪乯丅
仦乽梊慖夛倴倱杮慖乿
- 弌応峑偑堘偆乮梊慖夛偵僔乕僪峑偼弌応偟側偄両乯丅
- 梊慖夛偼墂揱偱偼側偄丅
- 侾慖庤偑憱傞嫍棧偼嬤偄丅
仦乽慡擔杮倴倱敔崻乿
- 弌応峑偼帡偰偄傞乮慡擔杮偵偼敔崻偺僔乕僪峑傕懡偔弌応偡傞乯丅
- 偄偢傟傕戝妛偺岞幃墂揱偱戝偒側戝夛偱偁傞乮嵟廔揑側栚昗偼嵟屻偺敔崻偩偑乯丅
- 侾慖庤偑憱傞嫍棧偼偐側傝慡擔杮偑抁偄丅
- 嬫娫悢偼敔崻侾侽嬫娫偵懳偟偰慡擔杮偼俉嬫娫丅
仏戝偒側岞幃墂揱偲偟偰懠偵弌塤偑偁傝傑偡偑丄弌塤偼慡擔杮傛傝傕偝傜偵嫍棧偑抁偔嬫娫悢偑彮側偔帪婜傕憗偄偺偱丄敔崻偺惉愌梊應偼慡擔杮偺惉愌偐傜峫偊傑偡丅
乽梊慖夛倴倱杮慖乿偱偼丄敔崻偺僔乕僪峑偑弌応偟側偄梊慖夛偺寢壥傪敔崻偺惉愌梊應偺拞偵慻傒崬傓娤揰偱峫偊傑偟偨丅偦偺専摙寢壥偵偼椺奜傕懡悢巆傝夵慞偺昁梫偼偁傞偺偱偡偑丄偲傕偐偔慻傒崬傫偱傒傑偟偨丅堦曽乽慡擔杮倴倱敔崻乿偱偼丄敔崻偺桳椡峑偺傎偲傫偳偑乽慡擔杮戝妛墂揱乿傕憱偭偰偄傑偡丅婎杮揑偵椉幰偺寢壥偺娭學偼嫮偄偼偢偱偡偑乮偙傟偑婎杮偺峫偊曽乯丄寢壥偵偼堘偄傕偱偰偍傝丄慡擔杮偺寢壥仺敔崻偺惉愌梊應偱偼丄慡擔杮偺寢壥傪慜採偵寢壥偑堘偭偨梫場偺僄僉僗傪怳傝偐偗傞偙偲偵側傝傑偡乮嵟傕戝偒側堘偄偼丄桳椡慖庤偺弌応乛寚応傕娷傔偨忦審偺堘偄偱偡偑丄偦傟偼偙偺暘愅偺栚揑偱偼側偄偺偱彍偒傑偡乯丅
仸乽梊慖夛倴倱杮慖乿偼乽仭梊慖夛偐傜乿偺崁偵傑偲傔傑偟偨偑丄偦偙偱偼梊慖夛偲杮慖偺惉愌傪斾妑偟偰椉幰偺娭學傪専摙偟偰偄傑偡丅梊慖夛弌応峑偺拞偵偼慡擔杮偵弌応偟偰偄傞妛峑傕偁傝丄偦傟傜偺妛峑偺慡擔杮偺惉愌傪娫偵偼偝傫偱梊慖夛偲杮慖偺惉愌偺娭學傪専摙偡傞庤抜傕峫偊傜傟傑偡丅偟偐偟丄梊慖夛偲慡擔杮偺憃曽偵弌応偟偰偄傞妛峑偺椉戝夛傊偺椪愴懺惃偑摨偠儗儀儖側偺偐屄恖揑偵嫮偄媈栤偑偁傝乮妛峑偵傕傛傞傛偆偱偡偑乯丄偦偺傾僾儘乕僠偼嵦梡偟傑偣傫乮梊慖夛偼慡擔杮偺俀廡娫屻偱偡乯丅
埲壓丄億僀儞僩偵側傝偦偆側偙偲傪傕偆彮偟嵶偐偔惍棟偟偰傒傑偡乮偙傟偱傕僼傽儞偺曽偵偼摉慠偺偙偲偱偟傚偆偑乯丅偦偟偰偦偺億僀儞僩偵偳偆懳墳偡傞偐傪丄埲崀屄乆偵専摙偟偰偄偒傑偡丅
仦奺嬫娫偺屄惈乮嫍棧偺堘偄乯
椉戝夛偺嫍棧偺堘偄傪惍棟偡傞偲師偺傛偆偵側偭偰偄傑偡丅
- 敔崻偑嬫娫暯嬒俀侾丏俉俲倣側偺偵懳偟偰慡擔杮戝妛墂揱偼嬫娫暯嬒侾俁丏係俲倣丅
- 敔崻偺嵟抁嬫娫偑係嬫偺侾俉丏俆俲倣偱懠偺嬫娫偼慡偰俀侽俲倣傪挻偊傞偺偵懳偟偰丄慡擔杮偼俉嬫偺侾俋丏俈俲倣偑嵟挿偱乮桞堦敔崻側傒乯丄懠偺嬫娫偼慡偰侾俆俲倣埲壓丅
嫍棧偺堘偄偐傜惗偢傞憱攋帪娫傊偺塭嬁偵娭偟偰偼埲壓偺偙偲偑峫偊傜傟傑偡丅
- 僞僀儉嵎偼嫍棧偑墑傃傟偽奼戝偡傞偺偑戝敿偱丄敔崻偺惉愌偺専摙帪偵偼偦偺揰傪峫偊傞昁梫偑偁傞丅
- 偨偲偊偽丄敔崻傪憐掕偟偰侾嬫娫偺嫍棧傪俀侽俲倣偲壖憐偟丄慡擔杮偱偺嵎傪扨弮偵嫍棧偵斾椺偟偰奼戝偝偣傞偺偑堦偮偺庤偱偁傞丅
- 偨偩偟丄捠忢偼嫍棧偑怢傃傞偵偮傟偰儔僢僾僞僀儉偼棊偪丄偦偺棊偪崬傒偼椡偺側偄慖庤偺曽偑戝偒偄偙偲偑懡偄偑丄扨弮斾椺偱偼偦偺棊偪崬傒偼庢傝崬傔側偄乮偐偲偄偭偰暿偺曽朄偼崱偼峫偊偮偐側偄丅忋埵偺慖庤偑旘偽偟夁偓偰偄偰丄屻敿棊偪崬傓偙偲傕偁傞偑丄偦傫側偺偼傕偭偲庢傝偙傓曽朄偼晜偐偽側偄乯丅
仦奺嬫娫偺屄惈乮弌応慖庤乛嫍棧懷偺堘偄乯
- 桳椡慖庤偑弌応偡傞係嬫娫乮侾乛俀乛係乛俉嬫亖嫍棧偑挿偄曽偺係嬫娫乯偲懠偺係嬫娫乮偮側偓偺嬫娫乯側偳偲偄偆梫慺傕偁傝傑偡乮椉曽偺惉愌暘晍偺堘偄偺塭嬁傪尒傞側偳偲偄偆偺傕丄丒丒丒丄僟儖儅忬懺偱尵偭偰傒偨偩偗偱偡乯丅
仦嬫娫悢偺堘偄
- 嬫娫悢偑敔崻偺侾侽嬫娫偵懳偟偰俀嬫娫彮側偄俉嬫娫丅
仏俉嬫娫偒偪傫偲慖庤傪弨旛偱偒傞妛峑偱偁傟偽塭嬁偼戝偒偔側偄偺偐側偲屄恖揑偵偼巚偭偰傑偡丅
仦慡擔杮偺惉愌傪敔崻偺惉愌梊憐偵巊偊傞宍偵偡傞
- 擭偵傛偭偰婥徾忦審摍偺幚巤娐嫬偑堘偆偺偱丄奺擭暿偺惉愌偼扨弮偵斾妑偱偒傑偣傫乮梊慖夛偐傜偺専摙偺帪偲摨條側曽幃偱巜悢壔偟傑偡乯丅
仏2009/2010乣2012/2013偺係僔乕僘儞傪懳徾偵暘愅偡傞偮傕傝偱偡丅
仦梊慖夛弌応峑偲旕弌応峑偺堘偄
- 嵟弶偵彂偒傑偟偨偑丄梊慖夛弌応峑偼偦偺俀廡娫屻偵慡擔杮偑偁傝丄旕弌応峑偲偼忦審偑戝偒偔堘偄傑偡丅梊慖夛弌応峑偼梊慖夛偺寢壥偐傜偺傾僾儘乕僠傪桪愭偟傛偆偲峫偊偰偄傑偡丅
仦偦偺懠乮専摙晄壜擻側憡堘梫場偲峫偊偰偄傑偡乯
- 摉擔偺懱挷偺堘偄
- 慡擔杮偵嶳偺嬫娫偼側偄乮嶳偺惉愌偺梊應偼偱偒側偄乯
婰榐昡壙偺峫偊曽
奺僔乕僘儞偺惉愌傪憡懳昡壙偟偰巜悢壔偟乮曃嵎抣乯丄偦偺巜悢傪嫟捠揑偵巊偆曽朄偱峫偊傑偡丅埲壓丄師偺棳傟偱夁嫀偺婰榐偺暘愅傪峴偄傑偡丅
- 慡擔杮偺婰榐偺惍棟
- 慡擔杮偺婰榐偺巜悢壔
- 慡擔杮偲杮慖偺娭學攃埇
- 慡擔杮偺寢壥偐傜偺杮慖偺弴埵偺梊應
埲壓丄忋婰奺嶌嬈偺億僀儞僩傪愢柧偟傑偡丅
仏侾乣俁偺嶌嬈偺弴斣偼彂偗偽偙偆側傝傑偡偑丄俁傪堄幆偟偰侾偲俀傪峴偆偺偱幚嵺偼暲峴揑偱偡丅
嶌嬈偺億僀儞僩
慡擔杮偺婰榐偺惍棟
慡擔杮偺婰榐傪惍棟偡傞嶌嬈偱偡丅側偍丄惍棟帪偺億僀儞僩偼師偺嶌嬈偱偡丅
- 慡擔杮戝妛墂揱偺婰榐偺俀侽俲倣傊偺姺嶼
扨弮偵憱攋帪娫傪嫍棧偵斾椺偝偣偰怢偽偟偰傒傞偮傕傝偱偡丅
仏僆儕僕僫儖偲斾妑偟偰戝偒偔堘偆孹岦偑弌傞偲婜懸偟偰偄傑偡丅
婰榐偺巜悢壔
梊慖夛偺帪偲摨條偵妛椡偺曃嵎抣偺掕媊偱巜悢壔偟傑偡丅
巜悢俿丂亖丂亅侾侽亊乮倶亅倣乯亐倱亄俆侽
- 倶丗奺峑偺婰榐
- 倣丗奺峑偺婰榐偺暯嬒抣 >
- 倱丗奺峑偺婰榐偺昗弨曃嵎乮僶儔僣僉乯
- 婰榐偼彫偝偄曽偑偄偄偺偱丄侾侽亊乮倶亅倣乯亐倱偺晹暘偵偼晧崋傪偮偗傑偡丅
仸敔崻杮慖偺婰榐偼丄乽仭梊慖夛偐傜乿偺崁偱惍棟乛巜悢壔嵪傒側偺偱巊偄傑傢偟傑偡丅
慡擔杮偲杮慖偺娭學攃埇
億僀儞僩偼師偺嶌嬈偱偡丅
- 椉戝夛偺巜悢偺暘晍恾偲昡壙
暘晍恾傪嶌惉偟丄椉幰偺娭學傪妋擣偟傑偡丅 - 婎杮儌僨儖偺嶌惉
椉幰偺娭學偺婎杮儌僨儖傪峫偊傑偡丅 - 慡擔杮偲敔崻偺杮慖偺寢壥偺憡堘揰偺梫場偺専摙
憡堘晹暘傪専摙偟丄偦偺夝庍曽朄傪峫偊傑偡丅
慡擔杮偺寢壥偐傜偺杮慖偺弴埵偺梊應
婎杮儌僨儖傪壓晘偒偵丄憡堘揰偺夝庍偐傜惗傑傟偨曗惓傪巤偟偰梊應偟傑偡丅
暘愅嶌嬈
偼偠傔傞慜偵丄僨乕僞偺嶌傝曽傪曗懌偟偰偍偒傑偡丅
- 慡擔杮戝妛墂揱偺曃嵎抣偼丄娭搶偐傜偺弌応峑偩偗偱寁嶼偟傑偡乮奩摉偡傞2009亅2012偺係擭娫偼弌応峑偼侾俀峑偱偟偨丂亅丂僔乕僪榞偺俇峑偲娭搶偺梊慖榞偺俇峑偺寁侾俀峑偱丄敔崻偵弌応偟側偐偭偨妛峑傕娷傒傑偡乯丅
- 敔崻偺曃嵎抣偼慡弌応峑偱寁嶼偟傑偡乮2010亅2013偺係擭偺偄偢傟傕捠忢擭側偺偱婎杮揑偵偼俀侽峑偵側傝傑偡丅婞尃偑偁偭偨応崌偼丄慡懱惉愌偵偮偄偰偼婞尃峑傪彍偒丄嬫娫婰榐偺曃嵎抣偼丄婰榐偑偁傟偽婞尃峑傕娷傔偰寁嶼偟偰偄傑偡丅
慡擔杮偺婰榐偺惍棟
仸杮崁偺寢壥偼丄師偺乽仜慡擔杮偲杮慖偺娭學攃埇乿嶌嬈偺拞偱堦弿偵帵偟傑偡丅
慡擔杮偲杮慖偺娭學攃埇
亙椉戝夛偺巜悢偺暘晍恾亜
挷嵏懳徾偺2009/2010乣2012/2013偺係僔乕僘儞偱丄慡擔杮偲敔崻偺憃曽偵弌応偟偨偺傋係係峑偺惉愌偺巜悢偺暘晍恾傪帵偟傑偡乮係僔乕僘儞偱慡擔杮偵弌応偟偨偺傋係亊侾俀亖係俉峑偺拞偐傜丄曅曽偟偐弌応偟偰偄側偄妛峑丄偍傛傃敔崻婞尃峑傪彍偄偨偺傋係係峑偺婰榐偱偡乯丅
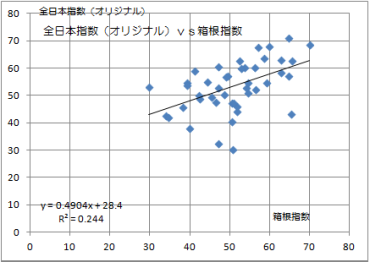
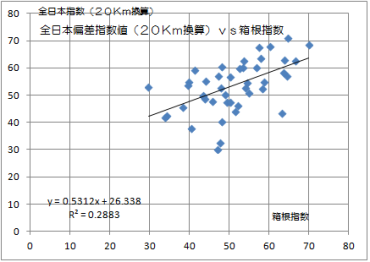
嵍偑慡擔杮乮僆儕僕僫儖乯倴倱敔崻丄塃偑慡擔杮乮奺嬫娫俀侽俲倣姺嶼乯倴倱敔崻偱偡偑丄丒丒丒丄僷僢偲尒偁傑傝堘偄傑偣傫乮俀侽俲倣姺嶼偺曽偑彮偟偼敔崻偺惉愌偵嬤偄傛偆偱偡偑乯丅屻偱傕偆偪傚偭偲嵶偐偔尒傑偡偑丄尰帪揰偺姶憐傪売忦彂偒偵偟偰偍偒傑偡丅
- 椉幰偺暘晍偵偁傑傝嵎偼傒傜傟側偄丅
仏婑梌棪乮僌儔僼偺俼丱俀偺抣乯偵嵎偑偁傝傑偣傫丅 - 婑梌棪傕崅偔側偄丅侽丏俆埵乮憡娭學悢偱偼侽丏俈埵乯偵偼側傞偺偐側側偳偲丄傏乕偭偲巚偭偰傑偟偨丅
壓偼丄偙偺僌儔僼偺尦偺昞偱偡丅昞偺悢帤偱傕戝偒側嵎偼側偄傛偆偵尒偊傑偡乮嵟傕戝偒側嵎偼丄俀侽侾侽擭偺擔戝偺俁丏俈俈偺僟僂儞乯丅
仦俀侽俲倣姺嶼昞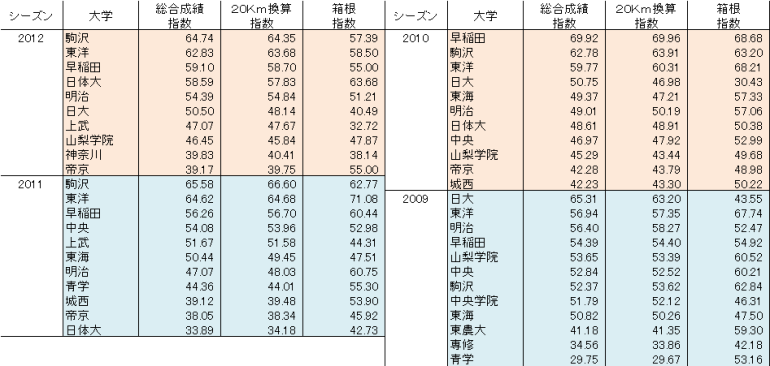
仸姺嶼偟偨曽偑庒姳婑梌棪偑崅偄偟丄嫍棧偺堘偄偼庢傝崬傫偩曽偑偄偄偲巚偭偰偄傞偺偱丄埲崀慡擔杮偺惉愌偺巜悢偼俀侽俲倣姺嶼偺曽傪巊偄傑偡丅
亙婎杮儌僨儖亜
婎杮儌僨儖偺専摙偺偨傔偵丄慜偺暘晍恾偵怣棅嬫娫傪擖傟偰傒傑偡乮曣暯嬒偺怣棅嬫娫偑拞懁偺椢偺俀杮偱奜懁偺僆儗儞僕偺俀杮偑屄暿抣偺怣棅嬫娫乯丅
仦怣棅嬫娫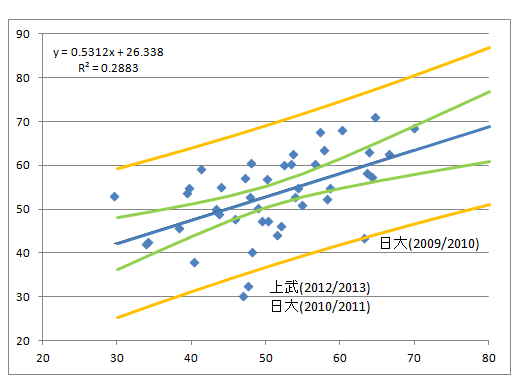
偙偺僌儔僼尒偰偺姶憐偼丠
仏偲傝偁偊偢偙傫側傕傫偩偲偄偆偙偲偱丄師偺専摙偱偡偹
亙慡擔杮偲敔崻偺寢壥偺憡堘揰偺専摙亜
傑偢偼偙偺昞偱偡丅偙偺昞偼嵍偵敔崻偺惉愌丄師偄偱慡擔杮偺惉愌傪巜悢宍幃偱懳斾偝偣偰暲傋偨傕偺偱偡丅偦偺拞偵娷傑傟傞俀侽乣俈侽偺奺棑偼丄奺嬫娫偺惉愌偺巜悢懷傪帵偟丄悢帤偼奩摉偡傞嬫娫悢偺崌寁傪昞帵偟偨傕偺偱偡乮偟偨偑偭偰奺戝妛偺悢帤傪崌寁偡傞偲丄敔崻偼侾侽偵慡擔杮偼俉偵側傝傑偡丅側偍丄抂偺俀侽戜偲俈侽戜偼丄偦傟偧傟偝傜偵偦偺奜懁偺懷堟傕娷傒傑偡乯丅偝傜偵偦偺塃懁偺俀楍偼丄俀侽俲倣姺嶼偺岠壥傪妋擣偡傞偨傔丄慡擔杮偺憤崌惉愌偲俀侽俲倣姺嶼偺巜悢偺嵎丄偍傛傃敔崻偲慡擔杮偺憤崌惉愌偺巜悢偺嵎傪傕偲傔偨傕偺偱偡丅
仦傑偲傔昞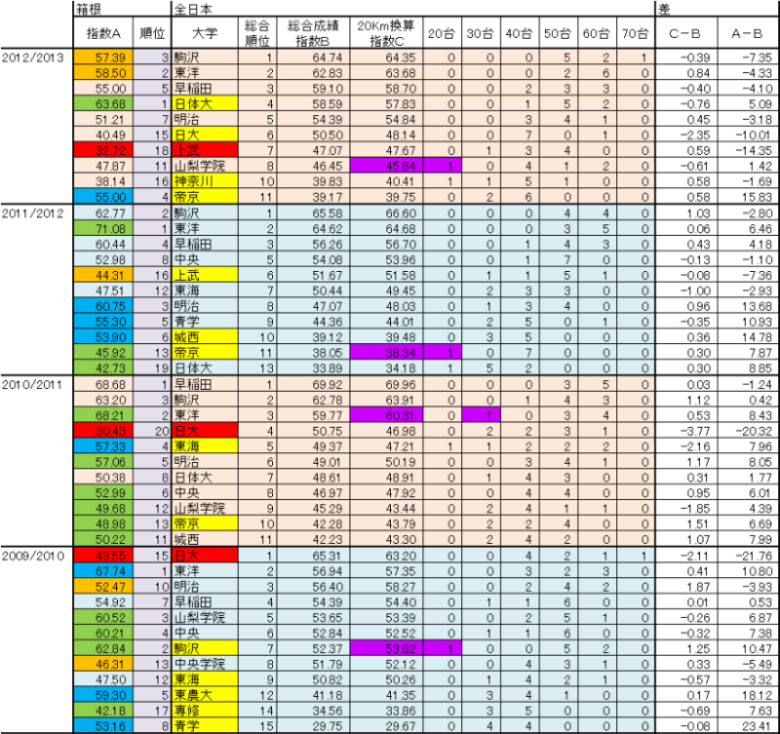
仏敔崻偺巜悢偺僙儖偺怓揾傝偼丄慡擔杮偐傜敔崻偱偺戝偒側曄壔傪帵偟傑偡丅
- 惵丗巜悢偑侾侽埲忋偁偑偭偨丅
- 椢丗巜悢偑俆乣侾侽偁偑偭偨丅
- 烌丗巜悢偑俆乣侾侽偝偑偭偨
- 愒丗巜悢偑侾侽埲忋偝偑偭偨丅
仏戝妛柤偺墿揾傝偼丄梊慖夛弌応峑偱偡丅
梊慖夛弌応峑偵惵揾傝偑懡偄偺偑旕忢偵婥偵側傝傑偡丅婥偵偟偰偄偨傛偆偵丄梊慖夛弌応峑偺慡擔杮偺惉愌偵偼儉儔偑偁傞傛偆偱偡丅
仺梊慖夛弌応峑偺惉愌偼彍偄偰婎杮儌僨儖傪嶌傞偙偲偵偟傑偡乮壓恾乯
仦怣棅嬫娫俀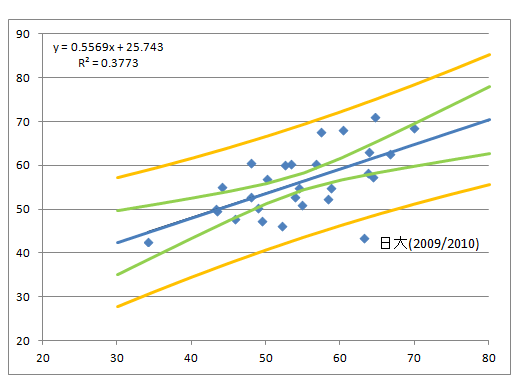
- 婑梌棪偼偐側傝忋偑傝傑偡丅偙傟傪嵦梡偱偡偹丅
- 慡擔杮偺巜悢偼寁嶼偟側偍偟偰偄傑偣傫乮曄偵傕巚偊傑偡偑丄慡擔杮偺弴埵偲幚椡偵娭楢偑偁傞偲峫偊傞側傜丄偦偺傑傑偺曽偑傛偄偲巚偄傑偡乯丅
憡堘梫場偺専摙乮帋峴乯
傆偨偮偺傾僀僨傿傾偑偁傝傑偡丅
亙俀侽俲倣姺嶼偺塭嬁亜
昞偺嵎偺悢帤偵娭偟偰丄偦偺晞崋偱暘偗偰悢傪悢偊偰傒傑偟偨丅
- 戞嘥徾尷乮俠亅俛丗亄丄俙亅俛丗亄乯丂丂侾俉
- 戞嘦徾尷乮俠亅俛丗亅丄俙亅俛丗亄乯丂丂丂俋
- 戞嘨徾尷乮俠亅俛丗亅丄俙亅俛丗亅乯丂丂丂俋
- 戞嘩徾尷乮俠亅俛丗亄丄俙亅俛丗亅乯丂丂丂俉
仏俠亅俛丗慡擔杮偺俀侽俲倣姺嶼巜悢儅僀僫僗慡擔杮偺僆儕僕僫儖惉愌巜悢
仏俙亅俛丗敔崻杮慖偺巜悢儅僀僫僗慡擔杮偺僆儕僕僫儖惉愌巜悢
戞堦徾尷偼懡偔丄俀侽俲倣姺嶼偺巜悢偑崅偄曽傕懡偄丅慜偵傕彂偄偨傛偆偵丄抁偄嫍棧偺嬫娫偱偼嵎偑偮偒偵偔偄偺偱丄扨弮偵嫍棧偵斾椺偝偣偰嵎傪寁嶼偟偰傕廫暘偱側偔丄俀侽俲倣姺嶼偺曽朄偱偼椉戝夛偺惉愌偺堘偄偺堦晹偟偐愢柧偱偒側偄偲偄偆偙偲偱偟傚偆丅
亙僽儗乕僉嬫娫偺塭嬁亜
抂揑偵偼丄慡擔杮偱僽儗乕僉傪婲偙偟偨帪偺懳墳偱偡丅慡擔杮偱僽儗乕僉傪婲偙偟偨妛峑偼敔崻偱偼僽儗乕僉傪婲偙偝側偄偲偡傞偲乮懕偗偰偼僽儗乕僉偼婲偙偝側偄偩傠偆偲峫偊傞乯丄媬嵪偡傞昁梫偑偁傝傑偡丅偦偙偱丄慜偺昞偵帵偡傛偆偵慡擔杮偺巜悢暿偺嬫娫悢傪悢偊偰昞偵偟丄掅偄曽偵娫偑偁偄偰悢帤偑擖偭偨応崌偵僽儗乕僉偲峫偊傞偙偲偵偟傑偟偨乮昞偺巼偵揾偭偨晹暘乯丅
仏梊慖夛偼丄侾俀恖偄偰戙傢傝偑偁傞偺偱峫偊傑偣傫偱偟偨丅
傑偨媬嵪曽朄偼丄偦偺嬫娫偺杮棃偺巜悢偼偦偺妛峑偺俀斣栚偵掅偄巜悢懷偵擖偭偰偄偨偲峫偊傞偙偲偵偟傑偟偨丅
椺丗俀侽侾俀擭偺嶳棞妛堾偼丄巜悢偺嵟壓埵偑俀侽戜偺侾恖偱丄偦偺忋偼係侽戜偺係恖偱偡丅偮傑傝娫偑偁偄偰偄傞偺偱丄嵟壓埵偺俀侽戜偺侾恖偼俀侽戜偱側偔係侽戜偲峫偊巜悢傪俀侽忋偘傑偡丅偦偟偰憤崌偺巜悢偱傕丄偦傟偵尒崌偭偨傛偆偵巜悢傪偁偘傑偡丅嬶懱揑偵偼丄偙偺帪偺奩摉嬫娫偼俆嬫偱俀侽俲倣姺嶼帪娫偺昗弨曃嵎偼侾丏係侾暘偱偟偨丅偟偨偑偭偰丄廋惓帪娫偼偦偺攞偺俀丏俉俀暘偲偟丄俀侽俲倣姺嶼偺憤崌惉愌偺昗弨曃嵎偼俇丏係俁暘側偺偱丄憤崌惉愌偺巜悢傪丄俀丏俉俀亊侾侽乛俇丏係俁亖係丏俁俋忋偘傑偡丅
愢柧傪傑偲傔傑偡丅
- 僽儗乕僉嬫娫偺擣幆
仏椺偱偼俀侽侾俀擭偺嶳棞妛堾戝妛偺俆嬫 - 僽儗乕僉嬫娫偱偺廋惓帪娫偺嶼弌
仏椺偱偼俀丏俉俀暘 - 曗惓巜悢偺嶼弌
仏廋惓帪娫亊侾侽乛憤崌惉愌偺昗弨曃
僽儗乕僉嬫娫偺塭嬁傪庢傝崬傓偺偼埆偔側偄偲巚偭偰偄傑偡偑丄廋惓検偺寛傔曽偼崀嶲偱偡丅寛傔側偄偲恑傑側偄偺偱丄偙偙偱偼壖偵忋婰悢帤偵偟偰偍偒傑偡丅偨偩栤戣偼傕偆堦偮偁偭偰丄奩摉働乕僗偑彮側偄偲偄偆偙偲偱偡丅
慡擔杮偺寢壥偐傜偺杮慖偺弴埵偺梊應
梊慖夛偺惉愌暘愅偺寢壥傪摜傑偊丄乽慡擔杮俀侽俲倣姺嶼巜悢丂vs丂敔崻杮慖暯嬒抣巜悢乿傪婎杮偵専摙偟傑偡乮徻嵶偼丄寢榑偺師崁偵帵偟傑偡乯丅
亙寢榑亜
埲壓丄梊慖夛偺寢壥偺曃嵎抣偲敔崻杮慖偺幚愌乛儌僨儖偲偺懳墳仺弴埵梊應偲偄偆峫偊偱丄偙傟傑偱偺専摙寢壥傪昞偵傑偲傔傑偟偨丅偙偺昞偑寢榑側傫偱偡偑偳偆偱偟傚偆偐乮乽怣棅尷奅乿偺僌儔僼偱尷奅偑埵偺俁峑傪彍偒傑偡乯丅
仦憤崌懳墳昞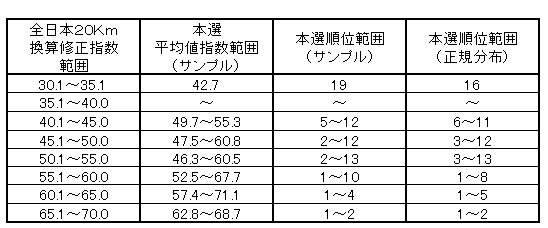
仏奜傟抣偺俁峑偲梊慖夛弌応侾俇峑傪彍偄偨偺傋俀俈峑偺幚愌偐傜嶼弌乮俀峑偼憃曽偵奩摉乯丅
仏慜弎偺傛偆偵丄梊慖夛弌応峑偺敔崻偺惉愌偺梊應偵偼梊慖夛偺惉愌傪嵦梡偡傞偺偱杮昞偼娭學偟側偄丅
寢榑傪傑偲傔傑偡丅
| 慡擔杮 巜悢 | 梊憐偝傟傞杮慖偺惉愌摍 |
|---|---|
| 俇侽埲忋 | 丒桪彑憟偄偵嶲壛丅 |
| 俆俆乣俇侽 | 丒僔乕僪尃偼妋曐偱偒傞丅 丒儀僗僩俁偵擖傞妛峑傕偁傞丅 |
| 係俆乣俆俆 | 丒僔乕僪傪妋曐偡傞妋棪偼掅偔側偄丅 丒儀僗僩俁傊偺怘偄崬傒偼擄偟偄丅 |
| 係侽乣係俆 | 丒僔乕僪偼傎傏妋曐偩偑丄摝偡妛峑傕偁傝丄儀僗僩俁偵怘偄崬傓妛峑傕偁傞丅 |
| 係侽埲壓 | 丒幚愌偑傎偲傫偳側偄乮偐側傝尩偟偔側傞丠乯丅 |
埲忋偱偡丅