予選会から
はじめに
予選会には、次の特徴があります。
- 12人が20Kmを走る。
- 実施時期は10月と本選に近い(シーズンの調子が推測できる)。
- 調整の走りはない(予選落ちはできない)。
- 集団走という予選会特有の走りがある(vs他大学ではなくvs時間の走り)。
本選では、突っ込んで入ったり(遅れてたらまず前につかなくちゃ)、前や後ろと離れた単独走の場面があって柔軟な対応が必要ですが、集団走ではそういう能力はわかりにくい。
この認識のもと、次の分析をやってみようとしています。
★過去の予選会と本選の成績を眺め、予選会の結果から予選会通過校の実力を推定する、つまり予選会で発揮したパフォーマンスの評価ということになります。
問題はあります。たとえば、
<成績の変換>
年によって気象条件等の実施環境が違うので、各シーズンを比較する際は、走破時間をそのままでは比較できない。
<予選会と本選の成績のねじれ>
本選と予選会では順位の逆転がかなりある(予選会の下位通過校が本選で上位へ、あるいはその逆)。この部分は、予選会の総合記録だけでは分析できません。本項では検討の対象外とし、巷間言われるねじれの要因を以下に列記するにとどめます。
- 5区が強いor弱い。
- 有力選手が予選会に出場できなかった。
- 予選会弁慶−集団走だと力が出るが、・・・。
- ピーキング
予選会と箱根駅伝の両方に調子を合わせるのは難しいとききます(一つの大会にきちんと合わせるも大変だと思いますが)。
以下試行過程をまじえて記述しますが、長くなるのでまず結果を示します(勝手に指数なんて作ってるんで、説明を読まないとわかりません−「読んでも、・・・」といわれるとつらいですが)。
| 予選会 中央値指数 | 予想される本選の成績等 |
|---|---|
| 55以下 | ・シード権確保は厳しいが、1校くらいは上位にくる(しかも6位以内にまでも)。 ・予選会の順位と本選の順位の上下関係にあまり関連がない。 *コンディション等で大きく順位が左右されるということですかね。 |
| 55〜65 | ・シード権は確保できる。 ・優勝争いには絡めない。 |
| 65〜75 | ・データがなく不明。 |
| 75以上 | ・確実に上位にきて、優勝争いに絡む。 |
*予選会中央値指数:予選会の成績を中央値を使って算出した偏差値で指数化(上位9校を対象に算出)−詳細後述。
記録評価の考え方
各シーズンの成績を相対評価して指数化し(偏差値)、その指数を共通的に使う方法で考えます。以下、次の流れで過去の記録の分析を行います。
- 予選会の記録の指数化
- 本選の記録の指数化
- 予選会と本選の関係把握
- 本選の指数と順位の関係確認
作業のポイント
予選会の記録の指数化
次の形式での指数化を考えています。
指数T = −10×(x−m)÷s+50
- x:各校の記録
- m:各校の記録の平均値 >
- s:各校の記録の標準偏差(バラツキ)
- 偏差値は、学力の偏差値の定義と同じです(記録は小さい方がいいので、10×(x−m)÷sの部分には負号をつけます)。
- 本選との関係データがとれるのは予選会通過の9校ですので、その9校の記録から算出します(9校は少ないんですが仕方がありません。なお、2012年の予選会出場校は45校)。
- 上位校のレベルはシーズンにより大きく変わり、平均値で指数を算出すると上位校のレベルの影響を受けます。その対策として中央値を取り入れた方法や、トリム平均を使った方法も取り入れて、以下の3種類の方法で指数化してみます。
- 平均値/標準偏差から算出した指数(平均値指数)
- 最上位校をカットした8校の記録から求めた平均値/標準偏差から算出した指数(トリム指数)
- 中央値と推定標準偏差を使って算出した指数(中央値指数)
*推定標準偏差 : 0.7413×IQR(四分位値範囲)
本選の記録の指数化
以下の3種類の方法で指数化してみます。
- 平均値指数(全20校対象)
- 中央値指数(全20校対象)
- 平均値指数(予選会通過校対象)
本選の中での位置づけなので、基本的には全20校を対象にして指数を算出します。ただし、本選と予選会で同じ力が発揮できたか考える時は予選会出場校の枠で考えた方がいいので、3の指数を使います。
また、本選には山があるので、5区を除く9区間の合計記録の指数も求めてみます。
予選会と本選の関係把握
- 予選会通過9校の両大会の指数を比較します。具体的には、9校×4年分=36校のデータの散布図を作成します。
- 散布図の傾向を分析します。
*5年ごとの記念大会は本選出場校が増えるので、通常の20校枠の、09/10シーズンから12/13シーズンまでの4シーズン分を対象とします(もう少し多い方がいいんですが、大変だし、またあまり古いと傾向が変わったりする可能性もあるので)。
*09/10シーズンは予選会から11校本選に出場しています(本選は20校)。そこで、予選会の上位9校だけを分析の対象にしました(なお、予選会の10位、11位は本選の20位、19位になっています、・・・、予選会の成績が本選直結ですね)。
本選の指数と順位の関係把握
正規分布を想定した場合と、指数(x)vs順位(y)の関係で作成した散布図の散らばり具合を使った場合で分析してみます。
分析作業
予選会/本選の記録の指数化
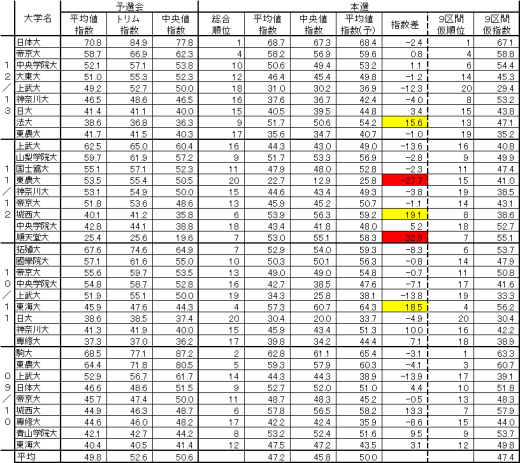
前項の方法で過去4シーズンの記録を指数化したのが下の表です。予選会出場校について感想を。
◇12/13シーズン
- 日体大は予選会では2位以下を大きく引き離した1位で、本選でも優勝でした。
- 帝京大は予選会2位で本選でも4位の好成績でした(平均値指数が58.7と他シーズンと比較して低くでています)。
- 法大が予選会実質最下位から本選では9位とジャンプアップしています。
◇11/12シーズン
- 予選会の上位は混戦で、本選では下位の成績でした。予選会の指数は他シーズンと比較して低く、上位校の予選会の指数は妥当と思います(ただし、予選会の8位と9位が、本選では予選会通過校の中での最上位2校になっています、・・・)。
- 城西大が予選会下位から本選では6位とジャンプアップしています。
- 東農大、順天堂大は、本選の平均値指数と予選会の平均値指数で差が25以上と大きくなっています(赤塗り部分)。
*東農大は5区が響き、順天堂大は予選会が悪すぎかな(ATがなければ予選落ち)。
◇10/11シーズン
- 東海大が予選会中位から本選では4位とジャンプアップしています。
◇09/10シーズン
- 駒大が予選会で1位になり、本選でも2位になっています。
- 予選会は上位2校が抜けた成績で、上位2校の中央値指数が高くなっています(本選の結果から考えると、やや高すぎる傾向あり)。
◇全体
- 平均値指数が一番ダメですね。全体的に指数が低くおさえられて上位の違いが出にくく、1位校の影響を大きく受けています。12/13シーズンや09/10シーズンは、予選会の1、2位校が本選でもその力を発揮しているシーズンですが、12/13シーズンの帝京大が60を切っちゃうのはねー。
- トリム指数は、予選会上位の学校は当然平均値指数よりは指数が増えるんですが、特に1位の学校の増え方が気になります(10/11シーズンなんかは増えすぎなんでしょうが、12/13シーズンはどっちなんだろう?)。
- 中央値指数が一番うまくとらえてますかね。10/11シーズンや11/12シーズンの予選会1位校が抜けて強いわけではないことをうまくとらえていると思います。ただ、09/10シーズンの1、2位はちょっと高すぎでしょう。
予選会/本選の指数の散布図
前記の表にもとづき次の5つの散布図を作成しました。
- 予選会平均値指数 vs 本選平均値指数
- 予選会平均値指数 vs 本選9区間仮指数
- 予選会平均値指数 vs 本選中央値指数
- 予選会中央値指数 vs 本選平均値指数
- 予選会トリム指数 vs 本選平均値指数
*散布図は、x軸が予選会指数、y軸が本選指数です。
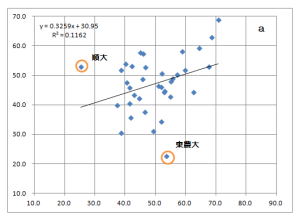
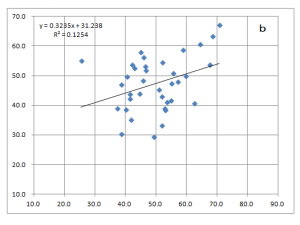
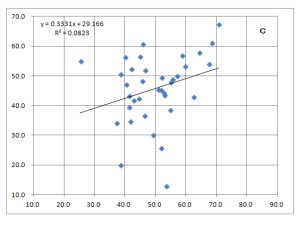
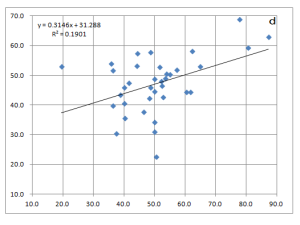
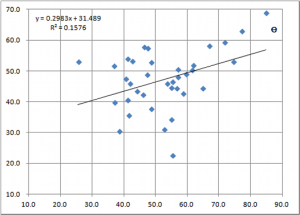
- 予選会の平均値指数は中央にまとまっている(チャートa〜c)。
- チャートaとbを比較すると、5区を入れないbの方が寄与率が若干高い(R^2の数字=予選会と本選の関連の強さを示す)。
*5区の影響で逆転してるわけですが、5区の強さを知る方法があるわけでなし、両指数の関連が元々低いし、・・・。 - 予選会の中央値指数とトリム指数は上位校の指数が高く、予選会の上位校の違いがはっきりでている(チャートd、e)。
- 本選の結果から予選会のレベルを考えると、09/10、12/13シーズンのレベルが高く、離れて11/12シーズン、10/11シーズンと見える=予選会の各種指数は妥当な数字である。
<各指数の評価>
- 平均値指数は図抜けた学校があると上位校の指数が低くなる傾向があるが、予選会のトップの実力はシーズンによってかなり違うのでよい指数でない可能性がある(なお本選は力のあるシード校が多数存在するので、予選会よりも影響は小さいと考えられる)。
- 中央値指数は全体のレベルをとらえるには適しているが、箱根駅伝での使用時には次のような問題がある。
たとえば、本選のトップ校の中央値指数は、13年の日体大が67.3、12年の東洋大が80.2、11年の早稲田大が77.9、10年の東洋大が65.6で、本選の総合時間とリンクしているように見える。これは、悪天候等による総合記録への遅れの影響が全校に一律にでるのでなく、トップレベルほど影響が大きくなると考えるとつじつまが合う。つまり、たとえば気象条件が悪いと、中央値指数では各校の力の違いが小さく見える可能性がある。 - トリム指数も平均値指数の弱点はカバーできている。ただし、1位校の指数の増え方にムラがある(2位と近いかどうかの影響が大きすぎるようです)。
⇒結論として、予選会は1項を重視して中央値指数を採用し、本選は2項を考慮して平均値の指数を使います。
予選会と本選の関係把握
前項の結論から、「d 予選会中央値指数 vs 本選平均値指数」を基本に、そこから外れ値を除いてさらに詳しく関係を見てみます
*予選会と本選で大きく違う結果は例外と考えそのデータを除くことにし(外れ値)、ここでは、予選会の平均値指数と本選の平均値指数(予選通過校のみで算出)で25以上の差の成績を除きました(正規分布を仮定すると2%の範囲で、表の赤塗り、すなわち11/12シーズンの東農大と順天堂大が該当します。なお15以上の差も黄塗りしました)。
次の図が、外れ値を除いた「予選会中央値指数 vs 本選平均値指数(34校版)」の図で、この図には回帰式の母平均と個別値の95%信頼区間を書き入れています(母平均の信頼区間が中側の緑の2本で外側のオレンジの2本が個別値の信頼区間)。
*34校版の他の組み合わせの図は示しませんが、予選会トリム指数を使うとR^2=0.2906、予選会平均値指数を使うとR^2=0.2548となっていて、本図のR^2=0.3354にはおよびません。
◇予選会中央値指数VS本選平均値指数信頼区間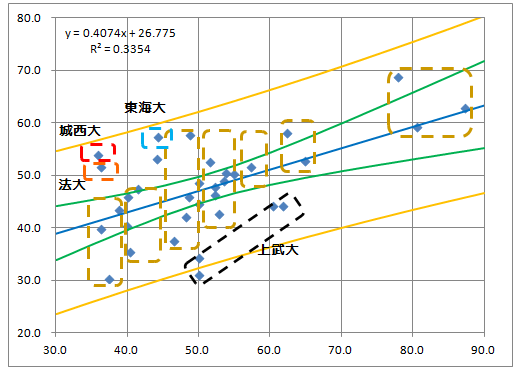
詳細な分析は最後のまとめの部分でやるとして、図を見ての感想を。
- サンプルが多いので、基本となる母平均の信頼区間はかなり絞れている。
- 成績の予測は個別値の範囲でするが、データの散らばりが大きく信頼区間の幅が広い(信頼率95%−他の部分のあいまいさを考えると厳しすぎる条件だが、少しくらい緩めても幅の広さはあまり変わらない)。
※標準偏差が大きく、本選の順位の予想は幅が広くなりすぎます。したがって、この後のまとめでは統計を離れ、現在のデータの傾向を使って仮説を立ててみます。
本選の平均値指数と順位の関係
◇本選平均値指数VS本選順位
下図は、4シーズンの本選の指数と順位の関係を各シーズンごとに折れ線グラフで表示したもので、シーズン毎の4本の線ができています。y軸の数字が順位なので、任意の順位に対して、一番右が指数の上端で一番左が下端になります(逆に言うと、たとえば本選の平均値指数が50〜55の範囲ならば、対応する順位は、上は11/12シーズンの5位から、下は10/11シーズンの11位までとなります。なお、12/13シーズンは2校棄権したのですが、そのまま使います)。
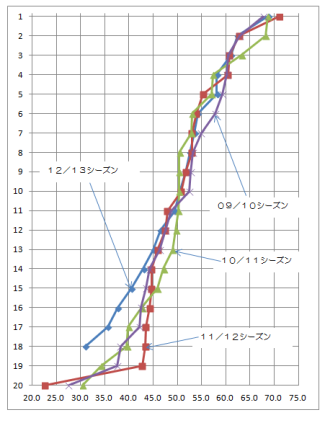
グラフの意味はなかったですね。各校の成績がランダムに散っていることが確認できたというそれだけですね(やってみて気づいてますが、これって累積の密度関数ですね)。
<結論>
以下、予選会の結果の偏差値と箱根本選の実績/モデルとの対応→順位予測という考えで、これまでの検討結果を表にまとめました。この表が結論なんですがどうでしょうか。
*予選会の中央値指数から本選平均値指数(サンプル)への対応付けでは、モデルの予測順位を絞り込むため、前項の表で黄塗りした平均値指数の差が15以上の学校と上武大も除きました(のべ27校の実績ということになります。なお、上武大は全4シーズン全てがかなり外れた位置にあって影響が大きいので除きました)。例外を多数作ることになりますが、ここでの主眼は箱根の順位検討の基本モデルを作ることにあるので、絞り込みを重視しました。今回はできてませんが、例外の中には、条件化が可能な個別の事情もあると思うので、将来的にはそれらを拾って順位予測の補正条件みたいな形で盛り込めればと思います。
- 予選会中央値指数 ⇒ 本選平均値指数(母平均) ⇒ 本選順位
- 予選会中央値指数 ⇒ 本選平均値指数(個別値) ⇒ 本選順位
- 予選会中央値指数 ⇒ 本選平均値指数(サンプル) ⇒ 本選順位
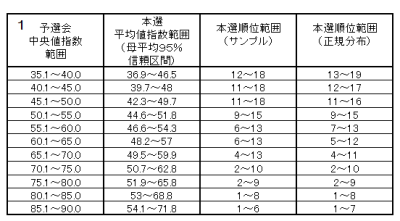
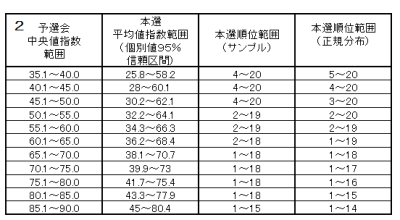
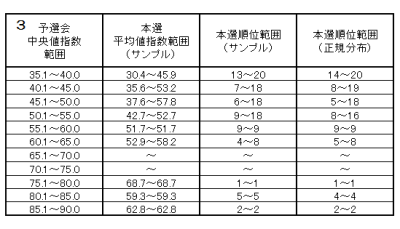
すぐにわかるのは、個別値の95%信頼区間(2の表)は広すぎて予想にならないということです。かといって、平均値の方は個別の学校の予想を全く保証してくれません。したがって、サンプルからでてくる指数とこれまでのデータからまとめることにしますが、実はこれは冒頭の表です(再掲します)。
*3の表はサンプルから対応を取っているので、「中央値指数範囲」と「本選順位範囲」が逆転しているところがあります。以前の表はこれを修正していたのですが、最終判断で修正すればいいのでサンプルの内容に忠実な値の表に変更しました。
| 予選会 中央値指数 | 予想される本選の成績等 |
|---|---|
| 55以下 | ・シード権確保は厳しいが、1校くらいは上位にくる(しかも6位以内にまでも)。 ・予選会の順位と本選の順位の上下関係にあまり関連がない。 *コンディション等で大きく順位が左右されるということですかね。 |
| 55〜65 | ・シード権は確保できる。 ・優勝争いには絡めない。 |
| 65〜75 | ・データがなく不明。 |
| 75以上 | ・確実に上位にきて、優勝争いに絡む。 |
◎4シーズンの実績を、最近勉強した初歩の統計の知識を使って分析してみました。今回の分析で外れ値とした分は、可能性2%なので仕方がないかと思います。しかし差が15以上で切った部分は15%以上の可能性があり、個別な事情がないか等の確認が必要ですが今回はできてません(確認できるのは、結果の数字から読み取れる範囲だけですが)。また上武大に関しては、本選で特に強く必要ななんらかの準備ができていないというような妄想はできるのですが、裏付けデータが準備できないと仮説にもなりません。
というように課題は山のようにありますが、今はかなりの疲労と限界を感じており、いったんは休憩します。