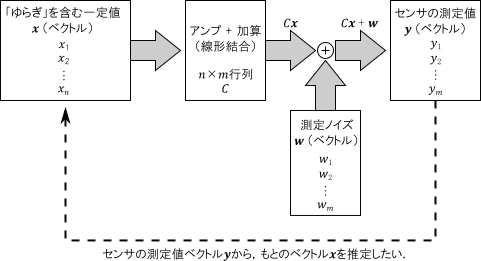
図1: 多変数の測定系
ここからは,複数の値を同時に測定するシステムで最大事後確率推定を行うことを考えます. これは,自動車の内部に付いている複数の温度センサの値を同時に取得して, それらの真値を一度に推定する場合などが該当します.
複数の信号“$x_1,\ x_2,\ \cdots, \ x_n$”をまとめて, 次のような$n$次元の「信号ベクトル」“$\bm{x}$”を作ります.
\begin{equation} \bm{x} = \begin{pmatrix} x_1\\ x_2\\ \vdots \\ x_n \end{pmatrix} \end{equation}何らかの測定系を使って信号ベクトル“$\bm{x}$”を測定し, 次の「測定値ベクトル」“$\bm{y}$”が得られたとします.
\begin{equation} \bm{y} = C\bm{x} + \bm{w} \end{equation}1変数の場合は,もとの信号“$\bm{x}$”をアンプで“$c$”倍に増幅するモデルを考えていました. 今回はこれを多変数に拡張して,測定系の構造を行列“$C$”で表しています. 例えば,ベクトル“$\bm{x}$”が2次元なら次のようになります.
\begin{align} \begin{aligned} C \bm{x} &= \begin{pmatrix} c_1 & 0 \\ 0 & c_2 \\ \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} \\ &= \begin{pmatrix} c_1 x_1 \\ c_2 x_2 \end{pmatrix} \end{aligned} \end{align}上式の行列“$C$”は,1つめの信号“$x_1$”に対する増幅率が“$c_1$”で, 2つめの信号“$x_2$”に対する増幅率が“$c_2$”であるようなアンプを含む測定系を表しています.
行列“$C$”の作り方によっては,次のように2つの信号を「線形結合」する(それぞれ定数倍して足し算する)システムにも対応できます. これは,測定過程で信号が「混ざる」ようなシステムだと考えられます.
\begin{align} \begin{aligned} C \bm{x} &= \begin{pmatrix} c_1 & c_2 \\ c_3 & c_4 \\ \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} \\ &= \begin{pmatrix} c_1 x_1 + c_2 x_2\\ c_3 x_1 + c_4 x_2 \end{pmatrix} \end{aligned} \end{align}行列“$C$”の列数は,ベクトル“$\bm{x}$”に合わせて“$n$”である必要があります. 一方で,行列“$C$”の行数は自由です. よって,ここでは行列“$C$”を一般の“$m \times n$”行列として扱うことにします. このとき,“$C \bm{x}$”は$m$次元ベクトルとなります. このベクトル“$C \bm{x}$”に対して雑音ベクトル“$\bm{w}$”を加えたものが,センサによる測定値ベクトル“$\bm{y}$”となります. ベクトル“$\bm{y}$”および“$\bm{w}$”の次元は行列$C$のサイズによって決まり,「$m$次元」となります.
\begin{equation} \bm{y} = \begin{pmatrix} y_1 \\ y_2 \\ \vdots \\ y_m \end{pmatrix} \end{equation} \begin{equation} \bm{w} = \begin{pmatrix} w_1 \\ w_2 \\ \vdots \\ w_m \end{pmatrix} \end{equation}なお,雑音ベクトル“$\bm{w}$”および測定値ベクトル“$\bm{y}$”の各要素は, それぞれ独立した値をとるものと考えます. 多変数になったとはいえ,測定系の構成は1変数の場合と基本的に同じです.これを図1に示します.

*2つの図を横に並べるテスト*
図2に本章の流れ,図3に時系列データの説明を示します.

図2: 本章の流れ |
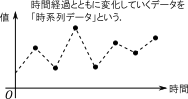
図3: 時系列データ |