問題ゼミナール ４
[１６]（オイラーの多面体公式の応用）
[１７]（２項係数）
[１８]（中間値の定理の応用）
[１９]（視点の変更）
[２０]（場合分けによる論証）
16｜17｜18｜19｜20
[１６]（オイラーの多面体公式の応用）
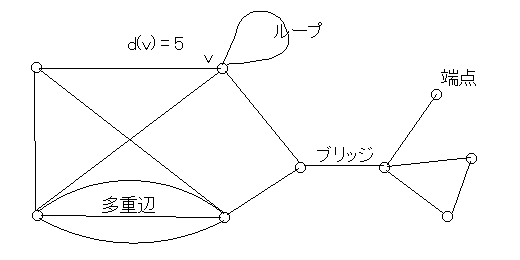
グラフＧの辺集合を E(G)，頂点集合を V(G) で表示する。
単に E や V と表示することもある。
頂点を 点 とよぶこともある。
ひとつの頂点をそれ自身に結ぶ辺を ループ 、
同じ２点が２本以上の辺で結ばれてるときそれらを 多重辺 、
ループも多重辺ももたないグラフを 単純グラフ とよぶ。
単純グラフＧの 補グラフ Ｇ’とは、 V(G) = V(G') で、
Ｇで結ばれてない２点が丁度Ｇ’で結ばれているグラフをいう。
グラフの点ｖに接合する辺の数 d(v) を ｖの次数 とよぶ。（ループは２回分かぞえる）
グラフが平面グラフ（plane graph）とは平面上に辺の交差なしで実現されてるとき、
グラフが平面的（planar）とは平面グラフとして実現できるとき
とする。
平面グラフＧの面集合を F(G) もしくは単に F で表示する。
面 ｆ について、その次数 d(f) は ｆ に接合してる辺の数とする。（ブリッジは２回分かぞえる）
単純グラフＧの頂点数が 11以上であれば、Ｇもしくはその補グラフＧ’
は非平面的であることを示せ。
＜Sol＞ 頂点数３以上の単純平面グラフ Γ においては、各面は３辺形以上であるから、
Σd(f) ≧ 3|F| ∴ 2|E| ≧ 3|F|
よってオイラーの公式により、
|V| - |E| + 2|E|/3 ≧ |V| - |E| + |F| = 2 ∴ |E| ≦ 3|V| - 6．
よって、もしもＧもＧ’も平面的とすると
|V|(|V| - 1)/2 = |E| + |E'| ≦ 6|V| - 12
となり、これは |V| ≧ 11 に反する。 //
[類題]
どんな単純平面グラフも次数が５以下の頂点を持つことを証明せよ。
＜Sol＞ 頂点の最小次数を δ とする。
|V|=1，2 のときはあきらか。
|V|≧3 のとき； δ|V| ≦ Σv∈V d(v) = 2|E| ≦ 6|V| - 12
∴ δ ≦ 6 - 12/|V| ＜ 6 ∴ δ ＜ 6． //
系 どんな平面地図も５辺形以下の面をもつ。
（∵） 「双対グラフ」をかんがえればよい。 //
[類題]
辺の数が丁度７の凸多面体は存在しないことを示せ。
＜Sol＞ 2|E| ≧ 3|F| （∵ 面は少なくとも３角形） かつ 2|E| ≧ 3|V| に注意する。
もし存在したとすると、 |F| ≦ 14/3 ，|V| ≦ 14/3 ∴ |F| ≦ 4 ，|V| ≦ 4
よって、 4 + 4 ≧ |V| + |F| = |E| + 2 = 7 + 2 ∴ 8≧9． これは不合理。 //
♯ 辺の数が６もしくは８以上であれば、そのような凸多面体は存在する。
（∵） |E|が偶数のときは、|E|=2n としてｎ角錐でＯＫ．
|E|が奇数のときは、(|E|-3)/2角錐のひとつの面に四面体をくっつければＯＫ．
もしくは底面の頂点の近くで切断してもＯＫ．
別の構成として、(|E|-1)/2角錐の底面を折り、あらためて角錐の頂点から
ジョインしてもＯＫ． //
[類題]
平面上のどの２本も平行でなくどの３本も１点で会しないようなｎ本の直線によって
平面はいくつの領域に分けられるか。
（ヒント： 直線どうしの交点をすべて内部に含む大きな円を描いて考える．）
[類題]
ある凸ｎ角形のタイルで平面が敷き詰められているときつぎを示せ。
（１） 半径Ｒの円を描いて内部に含まれているタイルがｉコ、円周と交わって
いるタイルがｂコのとき、b/i → 0 (R→∞)．
（２） ｎ≦６．
（ヒント： （２） C(R)の内部にあるか周と交わる i+bコのタイルから
平面グラフＧを構成し、オイラーの多面体公式を適用する。）
＜Sol＞ （１）． １個のタイルの面積は１としてよい。
半径Ｒの円を C(R) で表示する。
Ｒが十分大きいとき、円周と交わっているタイルは C(R-d) と C(R+d)
に挟まれた位置にある。
∴ b ≦ π(R+d)2 - π(R-d)2 = 4πRd.
また、C(R)の内部にあるタイル全体は C(R-d)を coverするので
i ≧ π(R-d)2.
∴ b/i ≦ 4πRd / {π(R-d)2} → 0.
（２）． ヒントに従って i+bコのタイルの辺と頂点からできるグラフＧを考える。
ただし、３本以上出会っている点のみを頂点とする。
凸性よりタイルの内角はπ未満ゆえ、円Ｃ(R)の内部にあるタイルの頂点は
Ｇの頂点である。
Ｇの頂点数、辺数、面数をｖ、ｅ、ｆで表示する。f = i + b + 1 である。
Ｇの頂点はどれも３次以上なので、3v ≦ 2e．
この不等式とオイラーの多面体公式より
2e ≦ 6f - 12．
またｎ辺形の面は少なくてもｉコあるので
ni ≦ 2e．
∴ ni ≦ 6f - 12 = 6(i+b+1) - 12．
∴ n - 6 ≦ 6・(b/i) - 6/i → 0． よって n - 6 ≦ 0． //
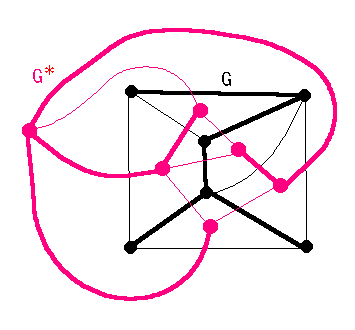《参考》 オイラーの多面体公式
凸多面体の頂点、辺、面の数を v、e、f
とすると， v - e + f = 2 ．
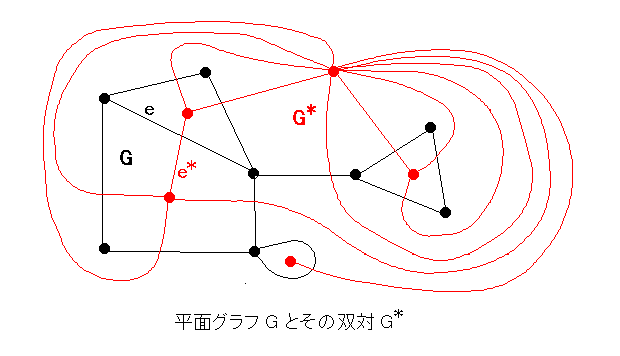
＜証明＞ 連結な平面グラフＧで示せばよい。
ＮをＧのひとつの生成木とする。
Ｔ = {e*|e∈Ｎc} は双対グラフＧ*の生成木である。
(v - 1) + (f - 1) = e ．
∴ v - e + f = 2 ．
（図で 太い黒線がＮ、太い赤線がＴ
v - 1 = |N|, f - 1 = |T|．） //
[１７]（２項係数）
最大公約数について （ n-1Cr-1 , nCr+1 , n+1Cr ）=（ n-1Cr , nCr-1 , n+1Cr+1 ）
が成り立つことを証明せよ。
＜Sol＞ rnCr = nn-1Cr-1
(n-r)nCr = (r+1)nCr+1
(n+1)nCr = (n-r+1)n+1Cr
∴ nCr = (n-r+1)n+1Cr-nn-1Cr-1-(r+1)nCr+1
またn-1Cr = nCr-n-1Cr-1
nCr-1 = n+1Cr-nCr
n+1Cr+1 = nCr+nCr+1
以上より左辺は右辺の約数。
n を n - r と置き換えて pCq= pCp-qを使うと、右辺が左辺の約数もいえる。 //
【 NOTE 】 rnCr = nn-1Cr-1 は両辺を計算して較べなくても n 元集合から１元をマークした r 元部分集合を選ぶ組合せを考えるとわかる。このような論法を「数え上げによる論法」という。
[類題]
すべての正整数ｎに対して 2nCnは n+1 の倍数であることを示せ。
次の等式を証明せよ。
(nC0)2 + (nC1)2 + (nC2)2 + ．．． + (nCn)2 = 2nCn
＜Sol＞ (1 + x)n(1 + x)n = (1 + x)2n の xn の係数を比較する。
もしくは、ｎ人の男子とｎ人の女子計２ｎ人からｎ人を選出する場合の数を考える。 //
[類題]
２以上の整数ｎと１以上ｎ未満の整数ｉに対して、不等式
(nCi)2 ≧ nCi-1・nCi+1
が成り立つことを数え上げ論法により示せ。
[類題]
Σk=mn nCk kCm = nCm 2n-m （n≧k≧m）
が成り立つことを数え上げ論法により示せ。
[類題]
Σk=0m mCk n+kCm = Σk=0m mCk nCk 2k
が成り立つことを数え上げ論法により示せ。
《参考》 パスカルの３角形
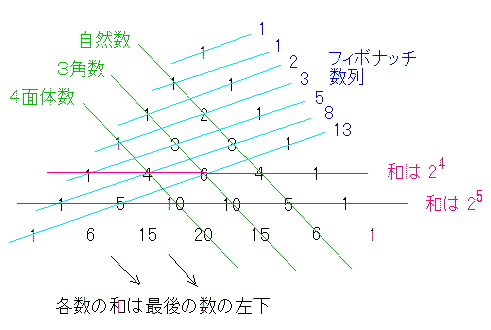２項係数は (a + b)n の展開（２項展開）の係数で
ｎ=０，１，２，．．．について上下に３角形状に並べたものはパスカルの３角形とよばれている。
パスカルの３角形では左図のようなことが成り立っている。
但し、フィボナッチ数列というのは
F1 = 1，F2 = 1，Fn = Fn-2 + Fn-1（n = 3,4,5,・・・）
で与えられる数列であり、また、たとえば、 1 + 3 + 6 + 10 = 20．
練習問題： 図の事実を証明せよ。
系 1・2 + 2・3 + 3・4 + (n - 1)n = (n - 1)n(n + 1)/3．
（∵） 「各数の和は最後の数の左下」の「対称版」の特別な場合として、
2C2 + 3C2 + ・・・ + nC2 = n+1C3．
両辺に２を掛けると題意の式を得る。 //
[１８]（中間値の定理の応用）
平面上の円ｃの中心をＯとする。ｃをグニャグニャと変形して閉曲線ｃ’とする。
このとき、ｃにある直径ＰＱがあって、この変形でのＰ，Ｑの移った先の点Ｐ’，Ｑ’
とＯは同一ライン上にあることを示せ。
＜Sol＞ ある直径ＰＱに対してＰ’とＱ’が一致すればＯＫゆえ、そうでないとする。
題意の直径ＰＱが存在しないと仮定する。
ｃのひとつの半径ＯＸとする。ＯＸを始線とするＯＰの偏角をθとし、ＯＰ’からＯＱ’
までの偏角を f(θ)とする。0≦θ≦2π， -π＜f(θ)＜π としてよい。
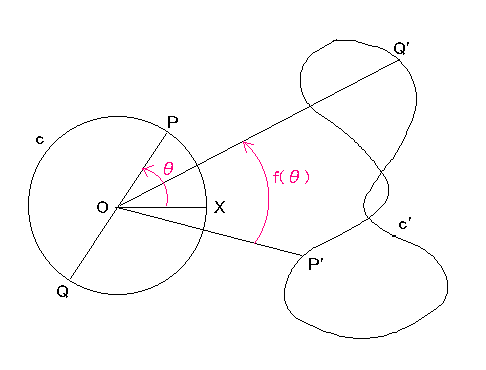
θが０から２πまでＰを連続的に（反時計回りに）動かすとき、
f(θ)も連続的に変化する。
θが 0≦θ0≦2πなるθ0からスタートしてＰがＱの位置まで行けば
ＱはＰの位置になる。
このとき、Ｐ’とＱ’も入れ替わるので f(θ+π) = - f(θ) となる。
すると中間値の定理によりθとθ+πの途中のξで f(ξ) = 0 となり矛盾。 //
[類題]
任意の凸多角形に対して、周長と面積を同時に２等分するような直線が
存在することを示せ。
[類題]
（１）空間内のかってな３角形は、水平面上に正射影したときの影が
正３角形となる位置に置くことが可能なことを示せ。
（２）更に、影が任意の３角形と相似となる位置に置くことができることを示せ。
[類題]
閉区間 [0,1] で連続、f(0) = f(1) をみたす実数値関数 f(x) がある。
ｎを２以上の整数とすると、
f(x0 + 1/n) = f(x0) ，0 ≦ x0 ＜ x0 + 1/n ≦ 1
なる x0 が存在することを示せ。
＜Sol＞ ai = f(i/n) - f((i-1)/n) （i=1,2, ... ,n） とする。
あるｉに対して ai = 0 であれば x0として (i-1)/n がとれるので、
任意のｉに対して ai ≠ 0．とする。
Σ[i=1〜n] ai = f(1) - f(0) = 0 より、相隣る ai、ai+1 で符号が反対のが存在する。
連続関数 g(x) = f(x + 1/n) - f(x) （x∈[0, 1 - 1/n]） は、x = (i-1)/n と x = i/n
で
正負が入れ替わるので、中間値の定理により、
0≦(i-1)/n＜x0＜i/n≦1 - 1/n なる x0 で g(x0) = 0． //
[１９]（視点の変更）
(a - b)3 + (b - c)3 + (c - a)3 を因数分解せよ。
＜Sol＞ a - b = X，b - c = Y，c - a = Z とおくと、
(与式) - 3XYZ = (X + Y +Z)(X2 + Y2 + Z2 - XY - YZ - ZX)
= 0 （∵ X + Y + Z = 0）
∴ (与式) = 3(a - b)(b - c)(c - a)． //
[類題]
正整数ｎに対して、0≦a≦b≦c≦n なる整数の３つ組 (a,b,c) の個数を求めよ。
＜Sol＞ 題意のような３つ組 (a,b,c) を {0, 1, ．．． , n + 2} の部分集合
{a, b + 1, c + 2} に対応させることにより、求める個数は n+3C3． //
[類題]
三角形の各頂点から対辺に引いた垂線は一点で交わることを
外心に帰着させて証明せよ。
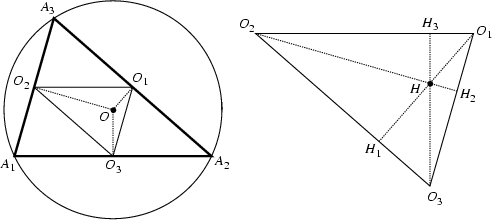
【 NOTE 】 垂心 Ｈ は垂足三角形 Ｈ1Ｈ2Ｈ3 の内心にもなっている。
[類題]
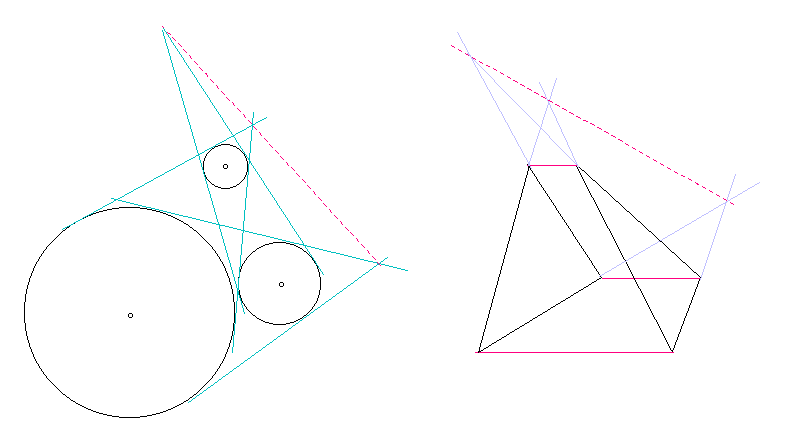
平面上の包含関係のない半径の異なる3つの円Ｃ1,Ｃ2,Ｃ3 に対して、
Ｃ2とＣ3，Ｃ3とＣ1，Ｃ1とＣ2の共通外接線の交点 Ｐ1,Ｐ2,Ｐ3は
同一直線上にあることを証明せよ。（モンジュの定理）
（ヒント： 「平面上のデザルグの定理」に帰着できる．）
[２０]（場合分けによる論証）
連立の不定方程式
a ＋ b = c × d ， c ＋ d = a × b
のすべての正整数解を求めよ。（出題：にゃぁにゃさん）
＜Sol＞ a ≦ b，c ≦ d とする。
どれかが１のとき； a = 1 とする。
1 + b = cd ∴ b = cd - 1． また 1b = c + d
∴ cd - 1 = c + d
∴ (c - 1)(d - 1) = 2
∴ c = 2, d = 3． b = 2 + 3 = 5． よって (a,b,c,d) = (1,5,2,3)
いずれも２以上のとき； 2d ≦ cd = a + b ≦ b + b = 2b ∴ d ≦ b
同様にして b ≦ d ∴ b = d
a + b = cd = bc， ab = c + d = b + c
辺々加えて a + b + ab = bc + b + c ∴ a(1 + b) = c(b + 1) ∴ a = c
よって
a + b = cd = ab ∴ (a - 1)(b - 1) = 1 ∴ a = b = 2 ∴ c = d = 2
よって (a,b,c,d) = (2,2,2,2)
以上より正整数解は
(a,b,c,d) = (1,5,2,3),(5,1,2,3),(1,5,3,2),(5,1,3,2),
(2,3,1,5),(2,3,5,1),(3,2,1,5),(3,2,5,1),(2,2,2,2) の９通り． //
[類題]
n = (abc + abd + acd + bcd - 1)/abcd が整数となるような自然数 a≧b≧c≧d＞1
の組 (a, b, c, d) をすべて求め、その a の値をすべて答えよ。（日本数学オリンピック予選１９９９ [9] ）
（ヒント： nabcd = abc + abd + acd + bcd - 1 より a,b,c,d は互いに素である。
特に a＞b＞c＞d ）
[類題]
平面上にいくつかの点が与えられていて、異なる２点間の距離は異なるとする。
どの点からも最短距離の点へ線分を引くとき、ひとつの点が６点以上と結ばれる
ことはないことを示せ。
＜Sol＞ 点ＴがＰ，Ｑと結ばれているとする。
（イ）Ｔから最も近い点がＰのとき；
ＱとＴが結ばれているから、ＴはＱから一番近い点である。
∴ ＰＴ＜ＱＴ＜ＰＱ
（ロ）Ｔから最も近い点がＱのとき；
同様にして、ＱＴ＜ＰＴ＜ＰＱ
（ハ）Ｔから最も近い点がＰ，Ｑ以外のとき；
このとき、Ｐから一番近い点もＱから一番近い点もＴ．
∴ ＰＴ＜ＰＱ かつ ＱＴ＜ＰＱ
以上どのケースでも線分ＰＱはΔＴＰＱの最長辺． ∴ ∠ＰＴＱ＞６０度．
Ｔの周りに６０度より大きな角は高々５コしかとれないから、
Ｔが６点以上と結ばれることはない。 //
[類題]
３×７のチェス盤の２１個の各マスを黒か白で彩色する。
どのように彩色しても、１辺の長さが２以上の長方形でコーナーの４マスが
同色のが必ずあることを証明せよ。
＜Sol＞ １列の彩色のパターンは
□ □ □ ■ □ ■ ■ ■
□ □ ■ □ ■ □ ■ ■
□ ■ □ □ ■ ■ □ ■
１ ２ ３ ４ ５ ６ ７ ８
の８とおりである。
ある１列がパターン１のとき； 残りの６列に１、２、３、４のどれかがあれば、
４スミが白のがある。
そうでなければ、他の６列は５、６、７、８のいずれかで、鳩ノ巣原理により、
これら６列中に同じパターンのがあり、題意の長方形が存在することになる。
ある１列がパターン８のときも同様に示される。
どの列もパターン１でもパターン８でもないとき； ７つの列に６つのパターンなので、
鳩ノ巣原理により、同じパターンのがあり、所望の長方形が存在することになる。 //
[類題]
４×４の正方形内に、９コの点が打たれている（境界含む）。
このとき、9Ｃ3個の三角形のなかに、面積が２以下のものが少なくとも
２つあることを示せ。また、３つの場合はどうだろうか。（出題：歩安彼さん）
＜Sol＞ ４行４列のチェス盤として考える。
対辺の中点どうしを結ぶと２行２列のが４コできる。
鳩ノ巣原理によりそのどれかには３点以上含まれる。
そのうちの３点で決まる３角形の面積は２以下。
よって４点以上含まれていれば成り立つ。
よって丁度３点が含まれてるとしてよい。
[その３点のうち丁度２点が同じ行か列にある場合]
同じ列にあるとしてよい。
残りの３列中その２点以外の７点のうちの３点以上を含むのがある。
これで決まる３角形も面積２以下。
[そうでない場合]
その３点は同じマスメＭに属している。
そのマスメを含む２行４列もしくは４行２列の長方形に他の点があれば
新たに面積２以下の３角形が生じるので、そうでないとする。
Ｍの位置は
（１）チェス盤の隅
（２）中央４マスのどれか
（３）それ以外
の３パターンで、いずれのケースも容易に確かめられる。
少なくとも３つあることを示すのは、めんどそうなので保留。 //
連続関数 ｆ：R → R が 加法的（ i.e. f(x+y) = f(x) + f(y) ）であれば、
f(x) = f(1)x となることを示せ。
＜Sol＞ 加法性より、x∈R，n∈N であれば、
f(nx) = f((n-1)x + x) = f((n-1)x) + f(x) = ... = nf(x) ------- (1)
とくに f(0) = f(2×0) = 2f(0) なので、f(0) = 0．
∴ f(x) + f(-x) = f(x + (-x)) = f(0) = 0 ∴ f(-x) = - f(x) ------- (2)
x = 1/m （m ∈ N） ならば、(1) より、
f(1) = f(m×(1/m)) = mf(1/m)． ∴ f(1/m) = f(1)(1/m)
よって x = n/m （m ，n ∈ N） ならば、 f(x) = nf(1/m) = f(1)x ------- (3)
(2)と(3) により、 x∈Q であれば、 f(x) = f(1)x．
また、 x∈R-Q （つまり x は無理数） であれば、 x に収束する有理数列 {xn}
を選べば、ｆの連続性により、 f(x) = lim f(xn) = lim f(1)xn = f(1)x． //
【 NOTE 】 不連続関数 ｆ：R → R が 加法的であれば、ｆのグラフは稠密（dense）
（i.e. どんなに小さな円板とも交わる）である。
練習問題： NOTE の命題を証明せよ。
（ヒント： ｆは不連続ゆえ f(a)≠f(1)a なる a∈R が存在する。
このとき、行列 A =
(1 a )
(f(1) f(a)) は正則であり、また、
(u,v)T ∈ Q2 ならば A(u,v)T はグラフに属する。）
[類題]
恒等的には０でない連続関数 ｆ：R → R が 条件 f(x + y) = f(x)f(y)
を満たせば、 f(x) = eax （a∈R） となることを示せ。
＜Sol＞ f(x) = f(x/2 + x/2) = f(x/2)f(x/2) ≧ 0
もしも f(0) = 0 とすると、 f(x) = f(x + 0) = f(x)f(0) = 0 で不合理。
∴ f(0) ＞ 0．
f(0) = f(x + (-x)) = f(x)f(-x) ＞ 0 ∴ f(x) ≠ 0 ∴ f(x) ＞ 0 （∀x ∈ R）
よって、合成関数 log f(x) が定義でき、それを g(x) とする。
この g：R → R は連続である。
g(x + y) = log f(x + y)
= log (f(x)f(y))
= log f(x) + log f(y)
= g(x) + g(y)
よって、g は加法的。 ∴ g(x) = g(1)x ∴ f(x) = f(1)x
g(1) = a とすると、 f(1) = ea． ∴ f(x) = eax //
成分が整数の２次行列Ａに対して、 An=I となる正の整数ｎがあれば、
そのようなｎの最小値は 1，2，3，4，6 のいずれかであることを示せ。
＜Sol＞ ある正則行列 Ｔ が存在して、T-1AT は
┌λ ０┐ ┌λ １┐
└０ μ┘ か └０ λ┘
であるが、条件より後者はありえない。
λn = μn = 1 なので、
λ= cos(2kπ/n) + i sin(2kπ/n) μ= cos(2mπ/n) + i sin(2mπ/n) （ 0 ≦ k ，m ＜n ）
λ+μ = tr A ，λμ = |A| ゆえ、共に整数。
よって、 sin(2kπ/n) + sin(2mπ/n) = 0
∴ cos(2kπ/n) = cos(2mπ/n) または - cos(2mπ/n) （ ∵ cos2 θ + sin2 θ = 1 ）
よって、 λ+μ = 0 または = 2 cos(2kπ/n) = 2 cos(2mπ/n)
前者のとき、λμ= - cos(4kπ/n) - i sin(4kπ/n) が整数より 4kπ/n = 0,π,2π,3π
∴ 2kπ/n = 0,π/2,π,3π/2 ∴ λ= -μ = 1, -1, i, -i
よって、 A2=I か A4=I
後者のとき、A=I , A2=I , A3=I , A6=I のいずれかが成り立つ。（確かめよ）
よって最小のｎは 1，2，3，4，6 のいずれかである。
┌1 0┐ ┌-1 0┐ ┌1 1┐ ┌0 -1┐ ┌-1 -1┐
└0 1┘,└ 0 -1┘,└-3 -2┘,└1 0┘,└ 3 2┘
がそれぞれの例となっている。 //
