問題ゼミナール ３

11｜12｜13｜14｜15

　[１１]（極値に着目する証明）

Ａを平面上の２ｎコの点の集合とする。これらのうちのどの３点も
共線（同一直線上にある）でないとする。
ｎ点を赤、ｎ点を青に塗り分けるとき、
　「ｎ本の線分がとれて、そのどの２本も共有点をもたず、各線分の
　　両端点は異なる色を持つＡの点である」
とできることを示せ。（パトナム問題）

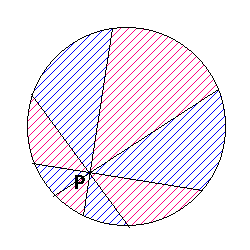
＜Sol＞　赤点と青点のペアリングのうち長さの総和が最小のが存在する。

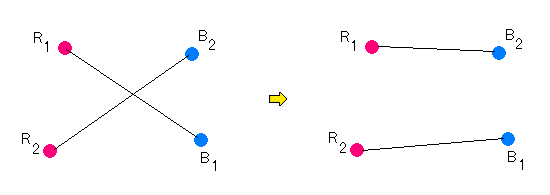
もし２本の線分Ｒ₁Ｂ₁とＲ₂Ｂ₂（Ｒ_iは赤点、Ｂ_iは青点）が交わるとそれを
Ｒ₁Ｂ₂とＲ₂Ｂ₁に変更すると長さの総和が減少する。これは不合理。　//

＜別解１＞ 帰納法で示す。

n = 1 のとき、明らか。n = 1,2, ... ,k のとき、成り立つと仮定。

n = k + 1 のとき； 題意の 2(k + 1) 点をＡとする。

Ａの凸包（包含する最小の凸集合）のある隣接する２頂点Ｐ，Ｑが異なる色
であるときは、Ａ - {Ｐ，Ｑ} でのペアリングと ＰＱ でＯＫ．

そうでないとき； Ａの頂点はどれも赤点としてよい。
水平でなくて、Ａのどの２点を結ぶ線分とも平行でなく、Ａのどの点もその左側にある
ような直線 Ｌ をとれる。この Ｌ を左に平行移動して行くことを考える。

Ｌ の左側にある赤点の個数から左側にある青点の個数を引いた値を D(L) とすると、
整数値の中間値の定理により、Ａを分断し D(L) = 0 であるような位置が存在する
ことがわかる。

分断された各々で、帰納法の仮定から、題意のペアリングがあるのでＡでのペアリング
ができることになる。　　　　　　//

＜別解２＞ ２ｎコの点をそれらを中心とする十分小さい半径εの円板におきかえる。
それぞれの色のｎコの円板の合計面積を等分するような直線Ｌが存在する。

２ｎコの点は「一般の位置」にあるので、
Ｌの両側に n/2 コずつに分けられるか、１種類の２コの円板がＬで２等分される
か、赤、青の円板が１コずつＬで２等分されるか のいずれかである。

どの場合も帰納的に示される。　　　　　//

【 NOTE 】 秋山とAlon は Ａをｄ次元空間内の一般的な位置にあるｄｎコの
点の集合としてこの問題を拡張した。その証明は別解２に従っている。

研究課題：　ｄ＝３で、面積の総和が最小だったら交わらない、といえるか。

[類題]
平面上にｎ点があってこれらのうちのちょうど２点のみを通る直線が存在しなければ
そのｎ点は同一直線上にあることを証明せよ。（シルベスターの問題）

＜Sol＞ ｎが０と１のときは自明に成り立つので ｎ≧２としてよい。対偶を示す。

ｎ点を A1、A2、・・・、An とし、これらのうちの２点で決まる直線を
L1、L2、・・・、Lm とする。 m ≦ _nC₂ なのでｍは有限である。

AiとLjの距離を d_ij で表す。あるd_ijは０でないことになる。
０でないd_ijのうち最小のを d_ab とする。

Lb が３点 Ai、Aj、Ak を通るとする。

Aa から Lbに垂線を下ろしたとき、 Aj、Ak はそれに対して同じ側にあるとして
一般性を失わない。
Aj と 直線 AaAk の距離 ＜ d_ab なので矛盾。　　//

[類題]
R² の開円板の有限個の族 F の合併の部分集合 E に対して、
F の互いに交わらない部分族 D1, ．．． , Dn で
3D1, ．．． , 3Dn の合併が E を含むのが存在することを示せ。
但し、3D は D と中心が同じで半径が３倍の開円板とする。（パトナム問題）
（ヒント： まず最大の開円板に着目する。）

[類題]
ｎコの連続している整数の積は n ! の倍数であることを証明せよ。

＜Sol＞ ｎコの連続している正整数に対して示せば十分なことはあきらか。

あるｎコの連続している正整数の積が n ! の倍数でないとして、
そのようなｎのうちで最小のを Ｎ とする。

このとき、ある非負整数ｍが存在して、
(m + 1)(m + 2)・・・(m + N) は N ! の倍数ではない。
そこで、このようなｍのうちで最小のを Ｍ とする。（ M＞0（∵ N ! は N ! の倍数））
(M + 1)(M + 2)・・・(M + N) は N ! の倍数でないことになる。

(M + 1)(M + 2)・・・(M + N - 1)(M + N)
= M (M + 1)(M + 2)・・・(M + N - 1) + N (M + 1)(M + 2)・・・(M + N - 1)

ＭとＮの選び方により、N ! は M (M + 1)(M + 2)・・・(M + N - 1) の約数で
(N - 1) ! は (M + 1)(M + 2)・・・(M + N - 1) の約数。

よって N ! は M (M + 1)(M + 2)・・・(M + N - 1) + N (M + 1)(M + 2)・・・(M + N - 1)
の約数であることになり仮定に反する。　　　　//

四辺形の対角線の長さの和は周長より小さいことを証明せよ。

＜Sol＞ 四辺形ABCDとする。ABが最短の辺と仮定してよい。

AC + BD ＜ (AB + BC) + (BA + AD) ≦ AB + BC + CD + DA．　//

[類題]
任意の平面４角形に対してある内点で４頂点までの距離の和が周長より短い
のが存在することを示せ。

＜Sol＞ 四角形 ABCD において BD ≦ AC としてよい。

　　BA ＋ BD ＋ BC ≦ BA ＋ AC ＋ BC ＜ BA ＋ (AD + DC) ＋ BC

よって頂点 B の十分近くの内点に対して成立する。　　　　　//

研究課題： 各頂点までの距離の和が周長より短いような内点をもつ
平面５角形を決定せよ。




　[１２]（複素数による等式の証明）

次の等式を証明せよ。　Σ_k=1ⁿ cos(2kπ/(2n+1)) = -1/2.

＜Sol＞ ω = cos(2π/(2n+1)) + i sin(2π/(2n+1))とすると
　ω²ⁿ⁺¹ = 1　∴ (1 - ω) (1 + ω + ω² + ... + ω²ⁿ) = 0
　∴ ω + ω² + ... + ω²ⁿ = -1

実部より　Σ_k=1²ⁿ cos(2kπ/(2n+1)) = -1

ここで　cos(2kπ/(2n+1)) = cos(2π - 2kπ/(2n+1)) = cos(2(2n-k+1)π/(2n+1))
　∴2Σ_k=1ⁿ cos(2kπ/(2n+1)) = -1
よって　Σ_k=1ⁿ cos(2kπ/(2n+1)) = -1/2.　　//

[類題]
次の等式を証明せよ。　Σ_k=1ⁿ cos(θ+ 2(k-1)π/n) = 0　（n ≧ 2）．

＜Sol＞
Σ_k=1ⁿ e^{i(θ+ 2(k-1)π/n)} = e^iθ(1 + e^2πi/n) + ... + e^2π(n-1)i/n)
　　　　　= e^iθ・(e^2πi - 1)/(e^2πi/n - 1)
　　　　　= 0

実部をとると与等式をえる。　　//

＜別解＞ 複素平面における原点中心の単位円のｎ円分点の和を 2π/n
回転しても不変なので、ｎ円分点の和は０． ｘ座標をとれば与等式を得る。　//




　[１３]（集合計算）

等式 (AΔBΔC)∪X = (A∪X)Δ(B∪X)Δ(C∪X)　（Nagataの公式）
を証明せよ。（Δ は対称差）

＜Sol＞ 一般のブール環R で示す。（すべての元がべき等である環をブール環）
chＲ=2（ ∵ x + x = (x + x)² = x²+x²+x²+x² = x + x + x + x　∴ x + x = 0 ）

x∪y := x + y + xy と定義すると
x∪(y1+y2+y3) = x + (y1+y2+y3) + x(y1+y2+y3)
　　　　　　　　= x + x + x + y1 + y2 + y3 + xy1 + xy2 + xy3
　　　　　　　　= (x∪y1) + (x∪y2) + (x∪y3)

ベキ集合Ｐ(A∪B∪C∪X)において加法をΔ、乗法を∩とするとブール環で、
J∪K = JΔKΔ(J∩K) となっている。　　//

[類題]
集合Ｓの部分集合Ａ，Ｂに対して A ∇ B を
　　　　　A ∇ B = (A Δ B)^c
と定義する。
この演算∇は結合的であることを示しなさい。

＜Sol＞ A ∇ B = A^c Δ B = A Δ B^c　なので

　　(A ∇ B) ∇ C = ((A Δ B)^c Δ C)^c
　　　　　　　　　　　= (A Δ B)^cc Δ C
　　　　　　　　　　　= A Δ B Δ C
　　　　　　　　　　　= A Δ (B Δ C)^cc
　　　　　　　　　　　= (A Δ (B Δ C)^c)^c
　　　　　　　　　　　= A ∇ (B ∇ C)．　　//

練習問題：　対称差Δが結合的なことを示せ。

＜Sol＞ 全体集合 U とし、その部分集合 A に対して
（標数 2 の）特性関数 χ_A： U → {0,1} （= Z/2Z） を、

　　　　　　　　　　　　　　　　　0　　x ∈ U - A
　　　　　　　　χ_A(x) = ｛
　　　　　　　　　　　　　　　　　1　　x ∈ A

として定義する。 A = B ⇔ χ_A = χ_B である。

χ_(AΔB)ΔC = χ_AΔB + χ_C
　　　　　　　　= (χ_A + χ_B) + χ_C
　　　　　　　　= χ_A + (χ_B + χ_C)
　　　　　　　　= χ_A + χ_BΔC
　　　　　　　　= χ_AΔ(BΔC)

∴ (AΔB)ΔC = AΔ(BΔC)．　　　　　　　//

♯　結合的な演算を見出すのは思いの外むずかしい。
♯　結合的な演算１個に理論１個が対応してるといっても華厳の滝、
♯　もとい、過言ではない。

練習問題：　A∪(B∇C) = (B -A)∇(C -A) を示せ。




　[１４]（集合族）

Ｓを集合族とし γ⊆∪Ｓ とする。
　γがＳの cover ：⇔ ∀ｘ∈Ｓ、γ∩ｘ≠φ．
　γがＳの odd cover ：⇔ ∀ｘ∈Ｓ、｜γ∩ｘ｜≡１(mod 2)．
集合族Ｓに対して次は同値であることを示せ。（和は対称差Δ）
　（１）Ｓは odd cover をもつ．
　（２）｜Ａ｜≡１の任意のＳの部分族Ａに対して、ΣＡ≠φ．

＜Sol＞ （２）⇒（１）． Ｓのサイズ｜Ｓ｜によるインダクション。

｜Ｓ｜= 0 のとき； Ｓは奇ヒフクをもち（２）をみたしている。

｜Ｓ｜≧ 1 のとき； ｘ∈Ｓ とし、Ｓ-{ｘ} にインダクションを適用すると、
Ｓ-{ｘ} は奇ヒフク γ_x をもつ。
｜ｘ∩γ_x｜≡１ なら γ=γ_x.
よってすべてのｘについて、｜ｘ∩γ_x｜≡０としてよい。

ｘ∈Ｓ、ｙ∈Ｓ、Ｓの要素としてｘ≠ｙとし、γ_xy = γ_xΔγ_y とすると、

　　　　　　　　　　　　　　　　　　０　　ｚ∈ Ｓ- {x,y}
　　　　　｜ｚ∩γ_xy｜ ≡｛
　　　　　　　　　　　　　　　　　　１　　ｚ∈ {x,y}

よって ｜Ｓ｜≡０ならば Ｓ= {x₁,y₁,...,x_m,y_m} としたとき、
　　　　　γ = Σ_i=1^m γ_{x_iy_i} とおけばよい。

｜Ｓ｜≡１ のとき。 Ｓは（２）をみたすので
∃ｖ∈∪Ｓ、｜{x∈S| x∋v}｜≡１.
｜Ｓ- {x∈S| x∋v}｜≡０ ゆえ、
Ｓ- {x∈S| x∋v} = {x₁,y₁,...,x_m,y_m} としたとき、
　　　　　γ = Σ_i=1^m γ_{x_iy_i} Δ {ｖ}
とおけばよい。

（１）⇒（２）． 明らか。　　　　　　　//

[類題]
対称差Δで２元体｛０、１｝上極小従属なｎ元集合族Ｓの
交差対（非disjointなペア）はｎ-１コ以上あることを示せ。
（但し自分自身とのペアは除く）

＜Sol＞ Ｓの各元に頂点を対応させ交差する２頂点を結んで
えられるグラフ（交グラフ）を G(S) とする。

極小従属であることから G(S) は連結である。
よって辺の数、すなわち交差対の数、はｎ-１コ以上。　//

例 E = {1,2,3}上の（fullな）４元集合族Ｓを
Ｓ = {1,2,3,123}　（ただし 1 = {1}, 123 = {1,2,3} など） とする。

このＳについて　ΣＳ = 1Δ2Δ3Δ123 = φ. よってＳは従属。
Ｓの真部分族について総和はφとならないのでＳは極小従属。

交差対（非順序対）は　{1,123},{2,123},{3,123} の３コ。　//

♯ ちなみに 2-uniformなＳに対しては、
♯ 　　極小従属 ⇔ サイクル（「輪っか」）
♯ で、交差対はちょうど ｎコである。

集合族（Ｖ,Ｅ）において v ∈ e のとき、頂点ｖと辺ｅは接合（incident）してる
とよび v inc e、
e₁ ∩ e₂≠φ　のとき２辺 ｅ₁とｅ₂ は隣接（adjacent）してる
とよび e₁ adj e₂ で表示する。

v,w ∈ V　について
v 〜c w ：⇔ ∃e₁,e₂,・・・,e_n∈E、v inc e₁, e_i adj e_i+1, e_n inc w
列 e₁e₂・・・e_n を (v,w)-chain とよぶ。v 〜c v とする。
v 〜p w ：⇔ ∃π⊆E、Δπ=｛v｝Δ｛w｝（Δは対称差）
πを ｛v,w｝-path　とよぶ。

[類題]
次を証明せよ。
（１）〜c、〜p は Ｖ上の同値関係。
（２）Ｇのどの辺もサイズが２のとき、〜cと〜p は一致する。
（３）Ｇのどの辺も偶数サイズのとき，　v 〜p w ⇒ v 〜c w．

ｇ， ｆ₁，・・・， ｆ_kはベクトル空間Ｖの一次形式で、Ｎ，Ｎ₁，・・・，Ｎ_kはそれらの核とする。
Ｎ ⊇ Ｎ₁ ∩ ... ∩ Ｎ_k ⇔ ｇは ｆ₁，・・・，ｆ_kの一次結合　を示せ。

＜Sol＞ 右から左はトリヴィアル（trivial）。よって、左から右を示せばよい。

　By induction．

ｋ＝１のとき： ｆ₁＝０ ならば、Ｎ₁＝Ｖ ゆえ Ｎ＝Ｖ で ｇ＝０.
よってＯＫ．
ｆ₁≠０のとき。 Ker f₁はＶの超部分空間（極大真部分空間）。
f₁(α)≠０ となるα∈Ｖをとり

　　　　　　　　　　ｃ＝ g(α)/f₁(α)

とする。
一次形式 ｈ＝ g - cf₁ は Ker f₁上で０となり、
また h(α)= g(α) - cf₁(α) = 0． よって、ｈ＝０　∴ ｇ＝ｃｆ₁．

ｋ-１のとき成り立つとして ｋのとき：
ｇ'， ｆ₁'，・・・，ｆ_k-1' を ｇ， ｆ₁，・・・，ｆ_k-1 の Ｎ_k上への制限とする。
ｇ'， ｆ₁'，・・・，ｆ_k-1' は Ｎ_kの一次形式である。
α∈Ｎ_k で ｆ_i'(α)＝０（i=1, ... ,k-1） ならば、α∈Ｎ₁ ∩ ... ∩Ｎ_k
で ｇ'(α)＝０.
帰納法の仮定より、

　　　　　ｇ'＝ c₁ｆ₁' + ... + c_k-1ｆ_k-1'

となるスカラーc_iが存在する。
いま

　　　　　　　　　　ｈ = ｇ - Σ_i=1^k-1 c_if_i

とすると、ｈはＶの一次形式で、Ｎ_k上で０となる。
ｋ＝１のときより、ｈは ｆ_kのスカラー倍ゆえ ｈ = c_kf_k とすると、

　　　　　　　　　　ｇ = Σ_i=1^k c_if_i ．　　　　　　　　　//



　[１５]（積分）

平面上の境界が区分的になめらかな有界凸図形Ｃに対して、
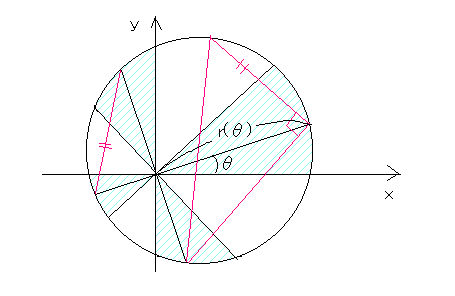
方位角θの平行２直線でＣをはさみつけたときの間隔を T_C(θ) とするとき
　　　∫₀^π T_C(θ)dθ = Ｃの周長
となることを証明せよ。

＜Sol＞ Ｃの周長は近似多角形Ｃ’の周長の極限で T_C'(θ)は T_C(θ)に一様に収束する。
よってＣは凸ｎ角形として示せばよい。

Ｃの周をなすｎコの線分をＣ₁、Ｃ₂、... 、Ｃ_nとし、 Ｃ_iの長さを L_iとする。

　　2T_C(θ) = Σ_i=1ⁿ T_Ci(θ)
　　∫₀^π T_Ci(θ)dθ = ∫₀^π L_isinθdθ = 2L_i

∴ ∫₀^π T_C(θ)dθ = (1/2)Σ_i=1ⁿ ∫₀^π T_Ci(θ)dθ
　　　　　　　　　= Σ_i=1ⁿ L_i
　　　　　　　　　= Ｃの周の長さ．　　　　　　　//

　系　平面上の境界が区分的になめらかな有界凸図形Ｃに対して
　　半径 r の円を境界に外接させて転がすとき
　　(中心の軌跡の長さ) = (Ｃの周長) + 2πr．

　系　半径ｒの円の周の長さは ２πｒ．