問題ゼミナール １
[０１]（図形とベクトル）
[０２]（偶奇性による論証）
[０３]（重みづけ）
[０４]（多面体）
[０５]（平均値の定理）
01｜02｜03｜04｜05
[１]（図形とベクトル）
六辺形ABCDEFにおいて AB//ED、BC//FE、CD//AF のとき、
△ACE = △DFB を示しなさい。（ハンガリー数学コンテスト）
＜Sol＞ ベクトルAB、BC、CD を a、b、c とすると
ベクトルDE、EF、FA は λa、μb、νc とおける。
よって、×を外積（ベクトル積）とすると、
(b + c)×(λa + μb) = λb×a + λc×a + μc×b
= λb×a + c×(λa + μb)
= λb×a + c×(-a -b -c -νc)
= λb×a + (a + b)×c
= (a + b)×(c + λa)．
∴ △ACE = △DFB． //
証明の系 ΔＡＥＣ//ΔＢＦＤ．
【 NOTE 】 元の問題は平面上だったかも。
コンテスト系の問題では一番印象に残ってるお気に入りの問題。
練習問題： 平面上とした場合を、（初等幾何的に）示しなさい。（ヒント： たとえば図の赤い三角形の面積と青い三角形の面積は等しい．）
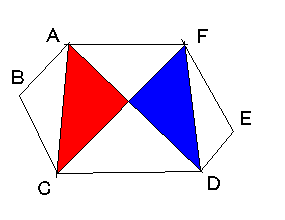
【 NOTE 】 三角形の２頂点を固定して残りの頂点を直線に沿って移動させると面積はたかだか１次関数的に変化する。このことを使うと一般に平行偶数辺形でも成立することがわかる。
研究課題： 平行偶数辺形の場合の NOTE とは別の証明は？
点 (a, b)、点 (c, d) を結ぶ線分と 点 (a', b')、点(c', d') を結ぶ線分が
交差しているかどうかを判定する方法を述べよ。（ヒント： 位置ベクトル
a = (a1 , a2) と b = (b1 , b2) に対して、
外積 a×b の大きさ a1b2 - a2b1 ＞ 0 ⇔ b は a から見てその左側
外積 a×b の大きさ a1b2 - a2b1 ＜ 0 ⇔ b は a から見てその右側．）
空間内に３点 A ，B ，C がある。原点 O として３つのベクトル a，b，c を
a = OA b = OB c = OC で定める。
このとき、A，B，C が同一直線上にあることは a×b + b×c + c×a = 0
と同値であることを示せ。
[類題]
四面体 ABCD において AB = CD、BC = DA とする。
AC の中点を P、BD の中点を Q としたとき、 AC⊥PQ⊥BD を示せ。
また、逆も成り立つことを示せ。
＜略解＞ １点 O からの位置ベクトル OA を a などと記す。
・は内積（スカラー積）とすると、
(a - d)・(a - d) = (b - c)・(b - c)
(a - b)・(a - b) = (c - d)・(c - d)
辺々引いて 2(p - q) = (a + c) - (b + d) に注意すると PQ⊥AC．
辺々加えて PQ⊥BD．
逆は逆にたどればよい。 //
[類題]
空間内のかってな４点A,B,C,Dに対して、
AB2 + BC2 + CD2 + DA2 ≧ AC2 + BD2
が成り立つことを示せ。
また、等号は四角形ABCDが平行四辺形の場合に限って成立することを示せ。
＜Sol＞
(左辺) - (右辺) = (b-a)2+(c-b)2+(d-c)2+(a-d)2-(c-a)2-(d-b)2
= (a-b+c-d)2 ≧ 0．
等号は a - b = d - c つまり BA と CD が平行かつ等しいとき。 //
♯ 平方は内積としての平方である。つぶれることもある。
ΔＡＢＣの外側にお互いに相似な三角形ＲＢＡ、ＰＣＢ、ＱＡＣを相似の向きが
一致するように底辺で接合させたとき、AP + BQ + CR = 0 となることを示せ。
＜Sol＞ ベクトルAQなどを単にAQで表示する。
またθ回転を Rθとかく。
∠CAQ = θ、AQ/CA = λ とすると
AQ + CP + BR = λRθ(AC + CB + BA) = 0
同様に QC + PB + RA = 0
∴ AP + BQ + CR = (AQ + QC + CP) + (BR + RA + AQ) + (CP + PB + BR)
= 2(AQ + CP + BR) + (QC + PB + RA)
= 0． //
【 NOTE 】 これは「三角形の３つの中線ベクトルの和は０」という性質の拡張になっている。
また、ｎ角形に容易に一般化できる。
[類題]
ΔＡＢＣの外側に底角が３０度の２等辺三角形ＲＢＡ、ＰＣＢ、ＱＡＣを
底辺で接合させるとΔＰＱＲは正３角形となることを示しなさい。（ナポレオンの定理）
＜Sol＞ 以下 AB、ACを b、cとする。θは３０度とする。
PQ = PC + CQ = (1/√3) Rθ(c-b) + (1/√3) R-θ(-c)
= (1/√3) (Rπ/2c - Rθb)
PR = (1/√3) (R-π/2b - R-θc)
R2θPQ = (1/√3) (R5π/6c - Rπ/2b)
= (1/√3) (-R-π/6c + R-π/2b) = PR
よってΔＰＱＲは正３角形。 //
練習問題： この解を、複素数による解に書き換えよ。
練習問題： ナポレオンの定理の「内側」版を示せ。
研究課題： 「モーレーの定理」をベクトルもしくは複素数を使って証明せよ。
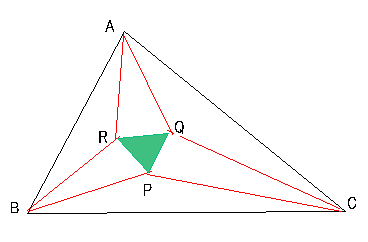
《参考》 モーレー（Morley）の定理
図のように６本の三等分線でできる三角形 PQR は正三角形である。
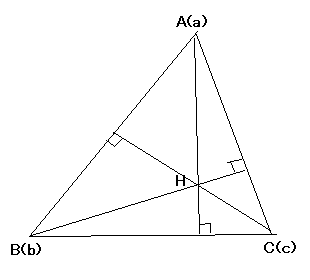三角形の各頂点から対辺に引いた垂線は
一点で交わることを証明せよ。（垂心定理）
＜Sol＞ 垂線の方程式は，
(c-b)・(x-a) = 0
(a-c)・(x-b) = 0
(b-a)・(x-c) = 0
これらの左辺の和は０ゆえ一点で交わる。 //
【 NOTE 】 異なる３直線： f(x) = 0， g(x) = 0， h(x) = 0 のうちの少なくとも
２つが交わるとき、 λf(x) + μg(x) + νh(x) = 0 となるような０でない３数
λ,μ,ν が存在すればこれら３直線は１点で交わる。
【 NOTE 】 三角形の五心（内心・外心・傍心・重心・垂心）は、外心以外は
「チェバの定理」を使うと容易に示せる。外心は垂心に帰着できる。
《参考》 チェバの定理
三角形ABCと、AB上の点 X, BC上の点Y, CA上の点Zが与えられたとき、
XC, YA, ZB が一点で交わることと次式が成立することは同値である。
AX BY CZ
-- ・ -- ・ -- = 1
XB YC ZA
ただし、長さは自然に正負の符号でかんがえるものとする。
[類題]
空間内の平行六辺形の対辺の中点どうしを結んだ３本の直線は
１点に会することを証明せよ。
＜Sol（概略）＞ 六辺形をＡＢＣＤＥＦ、中点をＡＢＣＤＥＦＡと回るとき
順にＰ，Ｑ，Ｒ，Ｓ，Ｔ，Ｕ とする。
平面的な場合； ＡＤとＦＣの交点をＬ、ＣＦとＢＥの交点をＭ、ＥＢとＤＡ
の交点をＮ とする。
また、ＵＲとＭＮの交点をＸ、ＱＴとＮＬの交点をＹ、ＳＰとＬＭの交点をＺ とする。
CD：AF = 1：λ、AB：ED = 1：μ、EF：CB = 1：ν とする。
MX：XN = (1-νλ)(1+μ)：(1-μλ)(1+ν) などがベクトル計算で示せるので、
三角形ＬＭＮにおいてチェバの定理が使えて、１点で会することになる。
非平面的な場合；（by みゅうさん） AB + BC + CD + DE + EF + FA = 0
かつ ベクトルAB、BC、CD は一次独立 より、DE = - AB，EF = - BC，FA = - CD
である。
このことから、ＰＳ、ＲＵ、ＴＱ はそれらの中点で交わることが示される。 //
＜非平面的な場合の別解＞ ベクトル AB、BC、CD を a、b、c とすると、
ED = a、FE = b、AF = c で、AX = x とすると、
line PS のベクトル方程式は (c + b) × (x - a/2) = 0
line QT のベクトル方程式は (c - a) × (x - a - b/2) = 0
line RU のベクトル方程式は (a + b) × (x - c/2) = 0．（×は外積）
左辺を順に f(x)、g(x)、h(x) とすると、
f(x) - g(x) - h(x) = 0．
よって、１点に会する。 //
【 NOTE 】 平面上の場合、１：１をチェバ型に拡張でき、逆も成り立つ。
ひとつおきの辺を１点に縮めるとチェバの定理になる。
三角形ＡＢＣ に対して、BC[PA] + CA[PB] + AB[PC] = [0]
を満たす点Ｐは三角形ＡＢＣの内心であることを示せ。
但し、 [ ] はベクトルをあらわす記号とする。
＜Sol＞ BC = a ，CA = b ，AB = c とすると、題意の式より、
[AP] = ( b[AB] + c[AC] )/(a + b + c)
一方、辺 BC を c：b に内分する点を D とすると、
[AD] = ( b[AB] + c[AC] )/(c + b)
∴ AP // AD
AD は ∠A の２等分線ゆえ、このことから AP も ∠A の２等分線。
同様にして BP は ∠B の２等分線となるから、P は内心である。 //
練習問題： 逆を示せ。
座標平面や座標空間において座標がすべて整数である点を格子点という。
どの頂点も格子点であるような多角形を格子多角形という。
平面における格子正ｎ角形Γはｎ＝４、つまり正方形のみであることを示せ。
（ヒント： Γの辺のつくるｎコのベクトルを使ってΓを縮小することを考えてみよ。）
＜Sol＞ Γの１辺の長さは √( (整数)2 + (整数)2 ) の形の正の数で
一定数以下のこのような形の数は有限個しか存在しない。
したがって、Γは「辺の長さが最小」と仮定できる。
Γの周を左回りにたどるように各辺を向き付けしたｎコのベクトルを考える。
ひとつの格子点（例えば原点）を始点とするようにこれらｎコのベクトル
を平行に移動すると、ｎコの終点も格子正ｎ角形になる。
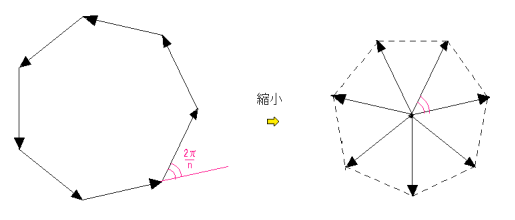
Γの外角は 2π/n で、1辺の長さの比は 1：2 sin(π/n) である。
n≧7 であれば 2 sin(π/n) ＜ 1 でΓの最小性に反することになる。
n=5 のとき； Γの頂点を左回りにＡ，Ｂ，Ｃ，Ｄ，Ｅ とする。
ＢＣ=ＡＡ’ などとなる点Ａ’，Ｂ’，Ｃ’，Ｄ’，Ｅ’ を考えると
A'B'C'D'E' はΓより小さい格子正５角形となり不合理。
n≠3，6 は容易に示される。 格子正方形の存在はあきらかである。 //
練習問題： 空間ではどうか。（コタエ： n = 3，4，6 のときのみ存在する。）
練習問題： 一般に、平面において、格子等辺奇数辺形は存在しないことを示せ。
＜Sol＞ xy平面上に相異なるｎコの格子点 P0，P1，・・・，Pn-1 があって
これらを順次結んだキョリ d(Pi-1,Pi) （i=1,2,...,n）
がどれも等しいとする。（但し、Pn = P0 とする．）
Pi = Pi(xi,yi) とする。
ai = xi - xi-1，bi = yi - yi-1，(d(Pi-1,Pi))2 = K とおくと、
ai2 + bi2 = K ----- (1)
Σai = Σbi = 0 ----- (2)
偶数の平方は 0(mod 4)、奇数の平方は 1(mod 4) ゆえ、
(A) ai，bi 共に奇数 ⇔ K≡2 (mod 4)
(B) ai，bi の一方のみ偶数 ⇔ K≡1 (mod 4)
(C) ai，bi 共に偶数 ⇔ K≡0 (mod 4)
(1)から ai，bi はすべての i について
一斉に (A)，(B)，(C) のうちのいずれかひとつになる。
(A) のときは、aiがすべて奇数なのでΣai = 0 となる為にはｎが偶数が必要である。
(B) のときは、ai + bi が奇数ゆえ、
Σ(ai + bi) = Σai + Σbi = 0 の為にはやはりｎが偶数が必要。
(C) のときは、ai，bi，K をそれぞれ ai/2，bi/2，K/4 に置き換えると、
(1)，(2)と同じ式になり、K≧1 だからこの操作を有限回繰り返して
(A)または(B)の場合に帰着でき、ｎは偶数であることになる。 //
[２]（偶奇性による論証）
自然数ｎに対して、その約数の総和が２ｎのとき ｎは完全数という。
素数ｓ、ｔに対して s2t2 の形の完全数は存在しないことを示しなさい。
＜Sol＞ s2t2 の約数の総和は (1 + s + s2) (1 + t + t2) である。
もしも s2t2 が完全だとすると (1 + s + s2) (1 + t + t2) = 2s2t2．
しかしこの左辺は奇数で右辺は偶数なのでそのようなことはありえない。//
練習問題： ほとんどそのままの証明で、一般に平方数であるような完全数は
存在しないことがいえる、ということを確かめよ。
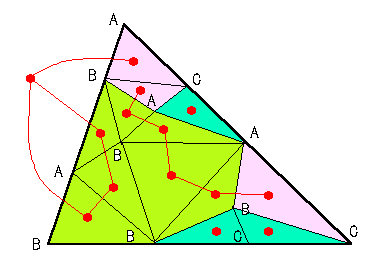３角形ＡＢＣの周上か内部にいくつかの点をとりこれらの点を頂点とする小３角形に
分割し、新しい頂点にラベルＡ,Ｂ,Ｃを
辺ＡＢ上の点はＡかＢ
辺ＢＣ上の点はＢかＣ
辺ＣＡ上の点はＣかＡ
内部の点はＡかＢかＣ
という規則で割りふる。小３角形でＡ,Ｂ,Ｃ３つのラベルを持つのの個数は
奇数であることを示せ。（Spernerの補題）
[類題]
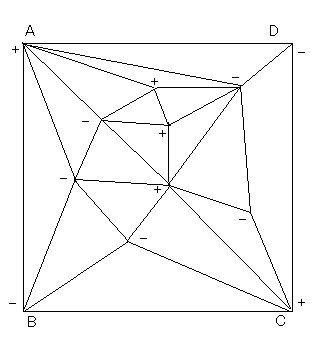図のように長方形ＡＢＣＤを三角分割して各頂点に符号 + - を割りふる。但しＡとＣ
には + , ＢとＤには ｰ を割りふる。
+ のみをたどってＡからＣに行けるか、または - のみをたどってＢからＤに行ける
ということを示しなさい。（ヒント： Spernerの補題を使う。）
＜Sol＞ + の頂点で + のみをたどってＡに行けるのを赤、
- の頂点で - のみをたどってＢに行けるのを青、それ以外のを緑で塗る。
塗り方のルールにより赤青緑の三角形が存在しないことは容易にわかる。
今、題意が成立しないとする。
ＡとＣを長方形の外側でＤのほう経由で結ぶと三角形ＡＢＣのみが３色の三角形
となり Spernerの補題に反する。 //
[類題]
偶数位数の群は、単位元 e 以外の元 x で x2 = e となるのをもつことを示せ。
[類題]
実数体 R は３次以上の奇数次の拡大体をもたないことを示せ。
＜Sol＞ ２次以上の有限次拡大体のひとつ E とし、α ∈ E - R とする。
奇数次数の実係数多項式はすくなくともひとつの実根をもつので、
αの既約多項式の次数は even で、 [R(α)：R] は even．
[E：R] = [E：R(α)][R(α)：R] より [E：R] も even． //
【 NOTE 】 この事実は ”代数学の基本定理” のガロア理論による証明で必要とされる。
《参考》 代数学の基本定理
１次以上の複素係数の多項式 f(x) は複素数の根をもつ。
＜証明＞ f(x) = Σaixi ∈ C[x] に対して、 f*(x) = Σai*xi （ai*
は ai の共役複素数）とすると、 f(x)f*(x) ∈ R[x] となり、
f(x)が複素根を持つ ⇔ f(x)f*(x)が複素根を持つ、
なので、１次以上の実係数多項式が複素根をもつことを示せば十分なことになる。
p(x) を R[x] の既約多項式、 E / R を C を含む (x2 + 1)p(x) の分解体とする。
ch R = 0 ゆえ、 E / R はガロア拡大。 G = Gal(E/R) とする。
|G| = 2mk （m は奇数） とすると、 シロー（Sylow）の定理により、G は位数 2m の
部分群 H をもつ。 B = EH を対応する中間体とする。
[B：R] = [G：H] = k で k は奇数ゆえ、類題より、 k = 1 であることになり、G は ２群である。
C に対応する G の部分群 Gal(E/C) について |Gal(E/C)| ≧ 2 であれば、 Gal(E/C) は
指数２の部分群をもち、対応する中間体は次数２の C の拡大となるが、
これはありえない（練習問題）。
∴ Gal(E/C) = 1 ∴ E = C ． //
＜別証明＞ f(z) = zn + a1zn-1 + . . . + an が複素数の根を持たないとする。
an = 0 であれば 0 を根として持ってしまうから an ≠ 0 である。
ft(z) （0≦t≦2） を
f0(z) = zn
ft(z) = tnf(z/t) （0≦t≦1）
f2-t(z) = f(t-z) （0≦t≦1）
と定義する。f1(z) = f(z) である。
z が原点中心の単位円を１周するときに ft(z) が描く閉曲線を Ct とする。
Ct は原点を通らない。（∵ C0 は 原点中心の単位円を n 回まわる閉曲線で原点を通らない。
0＜t≦1 のときはもし Ct が原点を通ると ft(α) = 0 となるαが単位円上にあることになり、f(α/t) = 0 となり矛盾。
1≦t≦2 のときはもし Ct が原点を通ると ft(α) = 0 となるαが単位円上にあることになり、f((-t+2)α) = 0 となり不合理。）
閉曲線 C0 は t が 0 から 2 まで連続的に変化するとき C2 まで連続的に変化する。
C2 は原点でない１点 an であるから原点中心の単位円を n 回まわる閉曲線 C0 が原点を通らないように連続的に変化して C2 になるのは不可能である。 //
練習問題： 複素数体 C は２次の拡大をもたないことを示せ。
[類題]
４ｎ＋３の形の完全数は存在しないことを証明せよ。（ヒント： 奇数の完全数Ｎの
素因数ｐが３(mod 4)のとき、Ｎの素因数分解におけるｐの指数ｅは偶数である
ことを示す。（by 歩安彼さん））
[類題]
正整数ｎに対して n2+1 の奇数の素因数は 4k+1 の形であることを示せ。
更にこれを拡張した次の命題を証明せよ：
２つの互いに素な正整数ｘ，ｙの平方の和 x2+y2 の奇数の素因数は 4k+1 の形である。
＜Sol＞ 奇数の素因数をｐとし、p = 2k+1 とする。
n2≡-1(mod p) であるから、両辺をｋ乗して、n2k≡(-1)k．
ｎはｐの倍数ではないから、フェルマーの小定理により、n2k=np-1≡1．
∴ (-1)k≡1．
ここでもしもｋが奇数だと -1≡1 となり、ｐが奇素数であることに反する。
よってｋは偶数で、題意が成り立つことになる。
（後半）
やはり題意の素因数をｐとする。
p|x とすると p|x2+y2 であるから p|y2．
したがって p|y となり、これは (x,y)=1 に反する。
よって (p,x)=1 で、ある整数ｌ，ｍ が存在して pl+xm=1．
∴ xm≡1(mod p)
∴ 0≡(x2+y2)m2≡1+y2m2 = 1+(ym)2．
よって、前半の結果から、題意が成り立つ。 //
練習問題： ４ｎ＋１の形の素数は無数にあることを証明せよ。
＜Sol＞ p=4n+1 を素数とする。ｐ以下の４ｎ＋１の形の素数のすべてと２との積
の平方に１を足した (2・5・13・・・・・p)2+1 をａ とする。
ａ が素数ならば４ｎ＋１の形でｐより大。
ａ が合成数ならばそのひとつの素因数ｑは奇数で、類題より ４ｎ＋１の形であり、
ａ は 5，13，・・・，p では割り切れないから q＞p ．
このことから帰結が従う。 //
♯ 「４ｎ＋１の形の素数が有限個で 5，13，・・・，p とする」と始めてもよい。
練習問題： ４ｎ - １の形の素数は無数にあることを証明せよ。
（ヒント： ４ｎ-１の形の素数が有限個で 3，7，11，・・・，p とし、
a = 4(3・7・11・・・・・p) - 1 とおく。）
《参考》 フェルマーの小定理
ｐが素数のとき、任意の正整数ａに対して、 ap≡a (mod p)．
とくにａがｐで割り切れなければ、 ap-1≡1 (mod p)．
♯ この２命題は同値で、どちらをフェルマーの小定理とよんでもいい。
練習問題： フェルマーの小定理を証明せよ。（ヒント： たとえば数学的帰納法．）
【 NOTE 】 フェルマーの小定理は次のように一般化できる（オイラーの定理）：
正整数ｎ，整数ａが (a,n)=1 であれば aφ(n)≡1 (mod n)．
ただし、φはオイラー関数で、φ(n)はｎ以下でｎと互いに素な正整数の個数。
♯ 初歩の「群論」を使えばエレガントに示せる。
練習問題： ５で割り切れない奇数Ｎを何倍かすると、全ての桁が９になることを示せ。
＜Sol＞ オイラーの定理により 10φ(N)≡1 (mod N) ゆえ。 //
練習問題： 任意の正整数 n に対して、2 のあるべき乗は ｎ個以上の連続した
0 をもつことを示せ。
＜Sol＞ オイラーの定理により、 2φ(5^(2n))≡1 (mod 52n)．
よって、ある整数ｋがあって、 2φ(5^(2n)) - 1 = k・52n．
両辺に 22n を乗じて移項すると、 2φ(5^(2n)) + 2n = 22n + k・102n．
ここで 22n＜10n ゆえ、2φ(5^(2n)) + 2n は所望のべき乗となっている。 //
[類題]
図のように１から１５の番号をもつコマが正方形の箱に入っている。
空きスペースを利用してコマをスライドして、左図の配置から右図の配置に
するのは不可能なことを証明せよ。（１５ゲーム）
* 1 2 3 1 2 3 4
4 5 6 7 5 6 7 8
8 9 10 11 9 10 11 12
12 13 14 15 13 14 15 *
＜Sol＞ 行列の辞書式に置換で表現すると
左図は (16,1,2,3, ．．． ,13,14,15) で奇置換であり、
右図は (1,2,3,4, ．．． ,14,15,16) で偶置換である。
□■□■ コマを１回スライドさせることは互換 (16,n) を施すことなので、
■□■□ 左図から右図にするには奇数回のスライドが必要である。
□■□■ 奇数回のスライドで 16 が移れるのは左図の
■□■□ 黒いところゆえ、不可能。 //
[類題]
６×６の正方形の部屋を１×２の畳で敷き詰めるとき、畳の縁でできる直線で
部屋を２つに分断するのが必ず生じることを示せ。（ロシア数学オリンピック）
＜Sol＞ 部屋を２つに分断する直線が現れないように敷き詰めできたとする。
この部屋を３６個の小正方形に分ける縦横５本ずつ計１０本の直線は、
どの直線も１枚以上の畳を横切ることになる。
小正方形の一辺を１とすると、どの直線も部屋を偶数面積の２つの長方形に分ける
ので、これら１０本の直線はどれも２枚以上の畳を横切ることになり、
合計で２０枚以上を横切ることになる。
これは、畳の枚数が１８枚であることに反する。 //
８×８のチェス盤上に８つの駒が各行および各列にひとつずつ配置されているとき、
黒いマス目の上に置かれた駒は偶数個であることを示せ。
＜Sol＞ 左上スミが白いマス目としてよい。
ｉ行ｊ列のマス目を (i,j) と座標表示する。
i + j が偶数 ⇔ (i,j) は白いマス目
i + j が奇数 ⇔ (i,j) は黒いマス目
駒が置かれている座標の総和は 2(1 + 2 + 3 + ・・・ + 8) で偶数
これらのことから題意が成り立つ。 //
[類題]
縦１０横１４のチェス盤のマス目に、次の条件を満たすように０または１を割りふる。
条件： 各行および各列には１が奇数個ある
このとき、黒のマス目にある１は偶数個であることを示せ。
＜Sol＞ タテ 2×3，ヨコ 2×5 で示す。
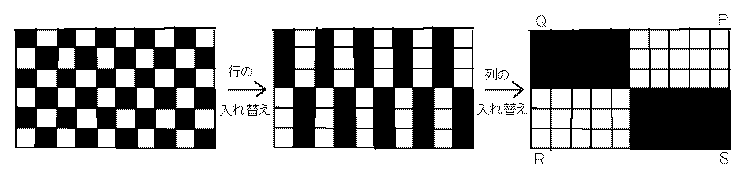
各行各列に１が奇数コという条件は行の入れ替えや列の入れ替えで不変である。
そこで図のようにして、P，Q，R，S に含まれる１の個数を p，q，r，s とすると、
条件より、p + q も p + s も奇数。
よって q + s は偶数で、黒マス中の１は偶数コ。 //
置換を互換の積で表すときの互換の個数の偶奇性が一定であることを、
差積を使わないで示せ。
＜Sol＞ ある {1, 2, ... . n} 上の置換が偶数個および奇数個の互換の積になったとすると
恒等置換が奇数個の互換の積で表せることになる。
恒等置換を奇数個の互換の積で表したときの最小の奇数を k ，その表示を
I = (i1 j1) (i2 j2) ... (ik jk)
とする。
互換 (i j) と (a b) の積のパターンはつぎの４通りである。（i,j,a,b は相異なる数字）
(i j) (a b) = (a b) (i j) ， (i j) (i j) = I
(i j) (i a) = (j a) (i j) ， (i j) (j a) = (j a) (i a)
k の取り方から (i1 j1) = (i2 j2) ではありえないから、
(i1 j1) と (i2 j2) の積は i1 が右側の互換にのみ含まれるような
互換の積に置き換えることができる。
この操作を繰り返すと、最終的に i1 が一番右の互換にのみ現れるような表示が得られる
ことになるが、このような表示は恒等置換の表示ではありえない。 //
[３]（重みづけ）
ｍｎ+１個の相異なる実数からなる数列には、長さｍ+１の増加部分列か
長さｎ+１の減少部分列が存在することを示しなさい。
（エルデス-セケレシの定理）
＜Sol＞ 題意の数列を a1,a2, ... ,amn+1 とする。
項 ai の増加性と減少性の重み wi+ と wi- を
wi+ は ａiから始まる最長の増加部分列の長さ
wi- は ａiから始まる最長の減少部分列の長さ
として定義する。
題意が成り立たないとする。
写像φ：{a1,a2, ... ,amn+1}→ [m]×[n] を
φ(ai) = (wi+，wi-)
として定義する。
i＜j のとき、
ai ＞ aj ⇒ wi- ＞ wj- ， ai ＜ aj ⇒ wi+ ＞ wj+
なので写像φは単射となる。
|{a1,a2, ... ,amn+1}| = mn+1 ＞ mn = |[m]×[n]|
ゆえこれは不合理。 //
【 NOTE 】 一般に全順序集合で成立する。
【 NOTE 】 サイズが大きい集合からサイズが小さい集合への単射が存在しない
というのは「鳩ノ巣原理」の一型である。（鳩ノ巣原理についてはココ）
[４]（多面体）
立方体をいくつかの四面体に分断するときの最少数を求めよ。（ロシア数学オリンピック）
＜Sol＞ Answer： ５．
理由： 四面体の各面は３角形なので立方体の各面に対して少なくとも２コの
四面体の面が必要である。
よって計１２コの四面体の面が要ることになる。
ひとつの四面体はそのうちの高々３コにしか寄与しえないので答えは
４以上ということになる。
しかしこれらの四面体の体積はせいぜい１/６（= 1/3×1/2×1）ゆえ４はありえない。
５コでは可能である。 //
[類題]
正八面体をいくつかの四面体に分割するときのその個数の最小値は
４であることを示せ。
任意の多面体Πに対して、Πの辺の長さの和はΠの直径の３倍以上であることを示せ。
＜Sol＞ Πの直径のひとつをＰＱとする。
ＰＱにＰとＱで垂直な平面を順にα、βとすると、Πはα、βの間もしくは
αかβ上にある。
α=α0をＰからＱに平行移動して行って最初にΠの頂点にぶつかるとき平面α1、
つぎにぶつかるとき平面α2、以下同様にしてβ=αnとする。
各αiαi+1間にはαiとαi+1をむすぶΠの辺からなる辺素（辺を共有しない）な
パスが
少なくとも３本存在する。このことから帰結が従う。 //
[類題]
（１）任意の凸多面体Πに対して、Πを平面で切った切り口の凸多角形 S
の周長 L(S) は Πの辺の長さの和 L(Π) より小さいことを示せ。
（２）これを精密化した次の不等式を示せ。 L(S) ＜ (2/3)L(Π)．
（Frankl-Maehara-Nakashima の定理）
＜Sol＞ （１）切断されてできた２つの多面体の一方の切断面以外の面の周長を
f1,f2, ．．．とし、もう一方の切断面以外の面の周長を g1,g2, ．．．とすると
2L(S) ＜ Σfi かつ 2L(S) ＜ Σgi
辺々加えて
4L(S) ＜ 2L(S) + 2L(Π) ∴ L(S) ＜ L(Π)．
（２）凸多面体 Π を切る平面への正射影をπとする。
必要であれば平面を少し回転させることにより
「Π の各面 F について、π(F) の面積は正」 と仮定できる。
π(S) は π(Π) に含まれる凸多角形なので、L(S) = L(π(S)) ＜ L(π(Π))．
よって、L(π(Π)) ＜ 2L(Π)/3 を示せばよい。
(1) 多角形 π(Π) の各(境界）辺 b に対して、π(e)=b となる Π の辺 e が
ただひとつ存在する。
(2) π(Π) の内部は正射影π により Π の面たちによって二重にカバーされる。
(3)多角形 π(Π) は Π の辺の像 π(e)たちによって、小多角形
Q1,Q2, ．．． に分割される。
(4)小多角形 Q で π(Π) の（境界）辺の２つ以上に接合するものは存在しない。
(5) 2L(π(Π)) ＜ L(Q1) + L(Q2) + ．．．．
また
[Π のすべての面 F についての L(π(F))の和] = L(π(Π)) + L(Q1) + L(Q2) + ．．．．
∴ 3L(π(Π)) ＜ L(π(F))の和 = 2L(Π) ∴ L(π(Π)) ＜ 2L(Π)/3． //
練習問題： （２）の不等式は best possible（最良） であること、
つまりいくらでも等式に近づくことを例示せよ。
どんな多面体にも同じ辺数の２つの面が存在することを示せ。
（ヒント： 最大辺数の面を選びそれに隣接してる面を考える。）
＜Sol＞ 存在しないとする。Ｆを最大辺数の面でｎ角形とする。
Ｆに隣接するｎコの面は３〜ｎ−１角形のｎ−３種類ゆえこれらのうちには
同じ辺数のがあることになり不合理。 //
【 NOTE 】 このように極値に着目すると呆気なく解けてしまう他の例
については 問題ゼミナール３ を参照されたい。
多面体 Π の頂点 P に対して Pの不足数 δ(P) を 2π から P に接合する面
での内角 P の総和を引いた数とする。
Π の頂点数、辺数、面数をそれぞれ v，e，f とすると
ΣP δ(P) = 2π( v - e + f )
となることを証明せよ。（ 組合せ Gauss-Bonnet の定理（ by Descartes ））
＜Sol＞ 面Ｆの辺数を nF で表す。
ΣP δ(P) = 2πv - ΣP ( P に接合する面での内角 P の和 )
= 2πv - Σ面Ｆ ( F の内角の和 )
= 2πv - Σ面Ｆ ( nF - 2 )π
= 2πv - πΣ面Ｆ nF + 2πf
= 2πv - 2πe + 2πf
= 2π( v - e + f ) //
[５]（平均値の定理）
０を含まない区間［a,b］で連続、（a,b）で微分可能な関数ｆ(x)に対して、a＜ξ＜b のξで
(af(b)-bf(a))/(b-a) = ξf '(ξ) - f(ξ)
となるのが存在することを示せ。 また、図形的な意味を述べよ。
＜Sol＞ Ｐ(x) = f(x)/x 、Ｑ(x) = 1/x に Cauchy の平均値を適用すると、
∃ξ∈(a,b)、(P(b) - P(a))/(Q(b) - Q(a)) = P'(ξ)/Q'(ξ).
このξは与式をみたす。
２点（a,f(a)）、（b,f(b)）を通る直線のｙ切片は (bf(a) - af(b))/(b - a)、
点（ξ,f(ξ)）における ｙ=f(x)の接線のｙ切片は f(ξ) - ξf '(ξ).
よって点(0,(bf(a) - af(b))/(b - a))からａとｂの間への接線が引けることを意味している。 //
関数 f：[0,1] → R は C2級（連続的２回微分可能）で、
f(0) = f(1) = 0 かつ、すべての x∈(0,1) について f(x)＞0 とする。
∫01 | f ''(x)/f(x) | dx ＞ 4 を証明せよ。
＜Sol＞ f(x) は 区間 (0,1) で最大値をとる。X∈(0,1) で最大値 Y をとるとする。
平均値の定理により、ある a∈(0,X) と ある b∈(X,1) が存在して、
f '(a) = ( f(X) - f(0) )/(X - 0) = Y/X
f '(b) = ( f(1) - f(X) )/(1 - X) = - Y/(1 - X)
∴ ∫01 | f ''(x)/f(x) | dx ＞ ∫ab | f ''(x)/f(x) | dx
≧ |∫ab f ''(x) dx |/Y
= | f '(b) - f '(a) |/Y
= | - Y/(1 - X) - Y/X |/Y
= | Y/(1 - X) + Y/X |/Y
= 1/X(1 - X)
≧ 4 ． //
[類題]
関数 f：R → R は C2級（連続的２回微分可能）で、
任意の x∈R について |f(x)|＜1， (f(0))2 + (f '(0))2≧2 とする。
このとき、 f(ξ) + f ''(ξ) = 0 となる実数 ξ が存在することを示せ。（パトナム問題（改））
＜Sol＞ G(x) = (f(x))2 + (f '(x))2 とおく。
平均値の定理より、
f '(a) = (f(0) - f(-2))/2 ， f '(b) = (f(2) - f(0))/2
なる点 a∈(-2,0)，b∈(0,2) が存在するので、
|f '(a)| ≦ (|f(0)| + |f(-2)|)/2 ＜ (1 + 1)/2 = 1
|f '(b)| ≦ (|f(2)| + |f(0)|)/2 ＜ (1 + 1)/2 = 1
∴ |G(a)| ≦ |f(a)|2 + |f '(a)|2 ＜ 2
|G(b)| ≦ |f(b)|2 + |f '(b)|2 ＜ 2
一方 G(0)≧2 であるから、G(x) はある点 ξ∈(a,b) で最大値をとり、
G '(ξ) = 2f '(ξ)[f(ξ) + f ''(ξ)] = 0．
f '(ξ) = 0 とすると、G(ξ) = (f(ξ))2 + (f '(ξ))2 = (f(ξ))2 ＜ 1
となるが、G(0)≧2 だから G(ξ)≧2 で不合理。 ∴ f(ξ) + f ''(ξ) = 0． //
Taylor の定理を使って e = lim(1 + 1/n)n が無理数であることを示せ。（ヒント： 2＜e＜3 を示しておく。背理法 ）
関数 f(x) は [0, ∞) で C2 クラスで、m0 = sup0≦x |f(x)| ,
m1 = sup |f'(x)| , m2 = sup |f''(x)| としたとき m0, m1
が有限とする。
このとき、 m1 ≦ 2 √(m0m2) を示せ。（ Hadamard ）
